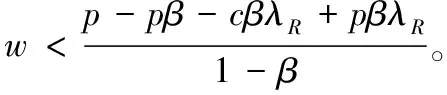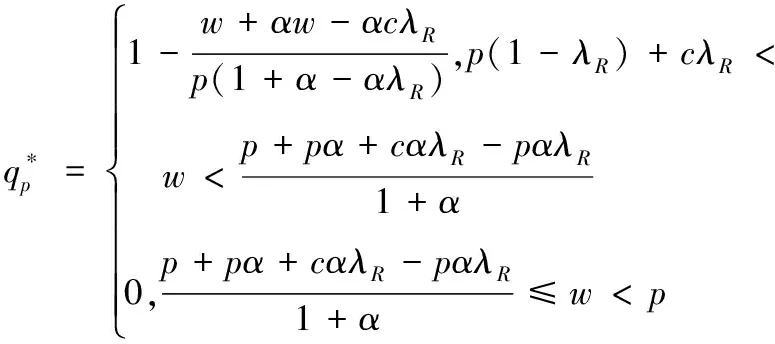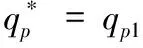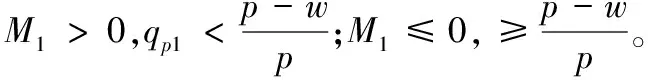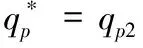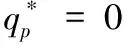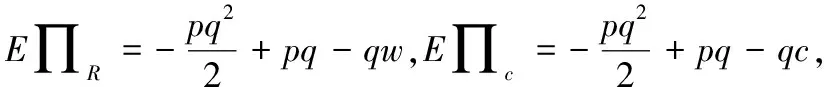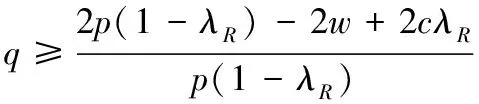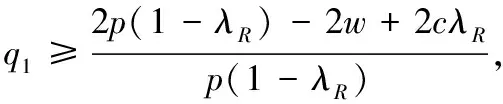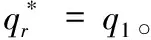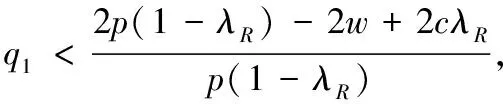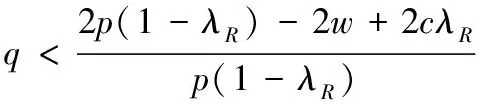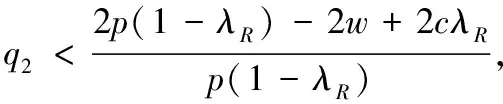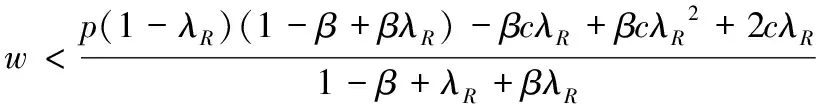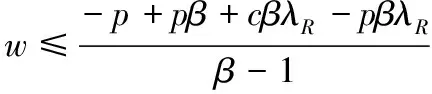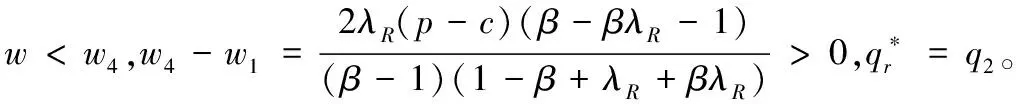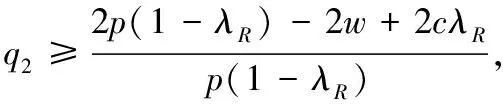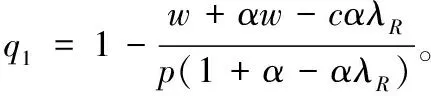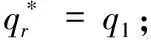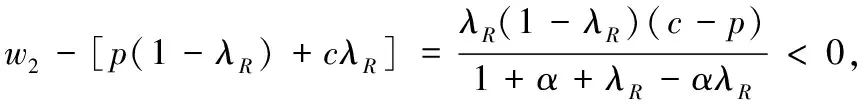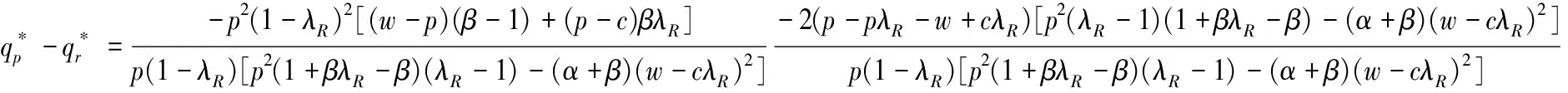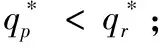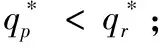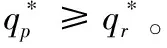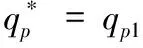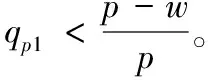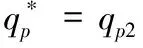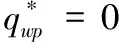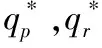具有公平感的零售商订购决策研究
李 娟,张 迪, 沈厚才
(南京大学工程管理学院,江苏 南京 210093)
1 引言
大量研究对传统经济学中“经济人”的基本假设提出了质疑,证实了决策者的行为普遍受到利他、公平感等社会偏好的影响。最后通牒博弈[1]、信任博弈[2]、独裁者博弈[3]等一系列的博弈实验都反复论证了人不是完全自私自利的,是注重公平的,在追求个人利益最大化的同时也关注收益结果分配是否公平。实践中,不仅仅存在追求双边公平的非“经济人”,也存在追求单边公平的非“经济人”。双边公平是决策者不仅关注自身也关注合作者遭受的不公平对待:当自己收益少于公平分配时会产生愤怒,当自己收益高于公平分配收益时会产生愧疚感,宁愿放弃个人部分收益以换取收益的公平分配。以咖啡交易为例,虽然咖啡饮品价格不断上扬,但是咖啡原豆价格却在过去10年间下滑了70%:在咖啡交易中咖啡农处于极度不平等的地位,其贸易利润大部分被原材料采购商所赚取。出于对公平贸易的追求,出现了“公平咖啡”,与没有标签的咖啡相比,贴有此标签的咖啡是采购商以更加公平合理的价格和契约从咖啡农处购买,保证咖啡农利益。单边公平是决策者仅关注自身遭受的不公平对待:当自身收益小于公平分配收益时会产生愤怒感,当自身收益高于公平分配收益时不会产生愧疚感甚至会产生愉悦感。譬如,中国廉价劳动力、较低环境成本吸引着从布偶,家具到电子产品等众多国际知名品牌到中国选择其代工厂,这类供应链上利润分配呈现“微笑曲线”势态。以苹果公司为例,截止2012年,其运营利润率突破30%,而其代工厂鸿海集团的利润率从2006年的4.0%降到2.0%的水平[4]。
学者们从不同角度去刻画公平,最常见的模型有三种。Fehr和Schmidt[5]将公平刻画为以自我为中心的不平等厌恶,在个体效用函数中融入了由于不平等所带来的个体效用损失,个体效用为个体自身收益及其他人收益的函数,记为FS模型,该模型中不平等厌恶由两方面组成:一方面是自己的收益高于对手所带来的有利不平等厌恶,另一方面是自己的收益低于对手所带来的不利不平等厌恶。Bolton和Ockenfels[6]提出了公平互惠竞争模型,记为ERC模型,该模型刻画了成员间的平等、互惠和竞争,认为人们不仅仅在意自己的金钱收益,同时也在意与其他人相比之下的相对收益,个体效用为个体自身收益及其相对收益的函数,当个体收益与群体平均收益相同时个体效用最大。Charness和Rabin[7]提出了基于社会总福利和互惠的公平模型,认为个体效用为个体自身收益,社会成员最小收益及社会总收益的函数,记为CR模型。
供应链系统中,成员进行决策时不仅考虑自身收益也会考虑自身收益在整个系统中的相对比例。有学者利用实验方法验证供应链中公平感对于成员决策的影响。Loch和Wu Yaozhong[8]通过实验验证了社会偏好会改变供应链中的成员行为。Pavlov和Katok[9]采用管理实验方法,说明了公平感和有限理性可以解释协调合同不总是能协调供应链的现象。
决策过程中个体对公平的感知,会从决策结果的公平性、以及决策程序的公平性两个视角考虑。组织行为学领域的文献论证了程序公平性对决策行为的影响。Thibaut和Walker[10]、Lind和Tyler[11]、Tyler和Blader[12]、McFarlin和Sweeney[13]对程序公平做了大量的研究;随后,Camerer, Ho和Chong[14]提出,对于有限理性行为的刻画,可分为两类:对随机事件结果的有限理性评估[15],以及对随机过程的有限理性学习[16]。因此在供应链中,当面对不确定需求时,零售商的公平关注会有两种:一种是关注比较每个随机状态的得益,将其称为过程公平;一种是关注比较在反复交易中形成的均衡状态,将其称为结果公平。
已有很多文献从不同角度研究了公平对供应链的影响。双边公平对供应链成员决策的影响有:Cui Haitao等[17]和Ozgun,Chen Youhua和Li Jianbin[18]分别利用FS模型分析了当需求函数为线性函数和非线性函数时,批发价合同下供应链系统成员的公平感知对系统收益的影响。他们的研究是在确定性市场需求下,不存在两种公平关注方式的差异。Chen,Hu和Song[19]采用Rotemberg[20]所提出的利他效用函数分析了不确定性需求下成员的利他行为,成员关注结果公平;得出,利他行为会减少供应链中的双边际化效应提高系统效率。Wu Xiaole和Niederhoff[21]基于一般性需求函数假设,研究了公平感对供应链成员间博弈行为的影响。
关于单边公平对零售商决策影响的研究:杜少甫等[22]在传统的两阶段供应链中引入公平关切,其中零售商是关注结果公平的,研究了不确定需求下公平关切行为对于供应链契约与协调的影响;指出零售商的公平关切不会改变供应链的协调状态。
本文研究不同类型公平感对于零售商的订购决策的影响。零售商面对的是批发价合同,采用FS模型刻画零售商的公平效用函数,将零售商的不同公平感类型与供应链系统结合研究其在不同公平类型下的订货量决策。假设需求函数服从均匀分布,Karlin[23]提出存在一种需求函数是波利亚频率函数(Polya frequency function),包括Gamma分布,[0,1]上的均匀分布和截尾正态分布;并且Anupindi,Bassok和Zemel[24],Schweitzer和Cachon[25]的研究中也假设需求服从均匀分布。
本文不同于已有研究主要体现在以下几个方面:第一,将公平分为四种类型:过程双边公平,结果双边公平,过程单边公平和结果单边公平,研究不同的公平感对于订货量决策的影响。第二,不同于已有文献,Cui Haitao等[17]中零售商通过价格设定来规避不公平感,本文中的零售商通过订货量的设定来规避不公平感;与Wu Xiaole和Niederhoff[21]的概括性结论相比,本文假设需求服从均匀分布,具体分析了公平感对零售商决策和收益的影响。
2 参数假设与基本模型
2.1 基本参数
由一个完全自利供应商和一个具有公平感零售商组成的系统,面临不确定性需求,供应商给定批发价,零售商确定订购量。不同于经典FS模型中零售商效用是其自身收益与供应商收益的比较,在本文中零售商效用取决于其实际收益与预期收益的比较,零售商认为的公平结果是相对于供应商的,即可将公平刻画为零售商对于自身收益在系统收益中的预期,这与Macneil[26],Frazier[27]是一致的。在本文中同Cui Haitao等[17],预期收益系数假设为外生的。零售商对于自己的收益状况有提前的预期,当零售商的实际收益小于预期收益时,零售商产生不利不公平厌恶(disadvantageous inequality aversion);当实际收益大于预期收益时,零售商产生有利不公平厌恶(advantageous inequality aversion)。
系统参数:
c:单位产品生产成本;
p:单位产品的零售价格;
w:单位产品的批发价;
x:不确定性需求,服从[0,1]上的均匀分布;
f(x)和F(x):分别为不确定性需求的概率密度函数、概率分布函数;
α:不利不公平的厌恶系数,当零售商实际收益小于其预期收益时,零售商感知到不利不公平,α>0;
β:有利不公平的厌恶系数,当零售商实际收益大于预期收益时,零售商感知到有利不公平,-α≤β<α,β<1;
∏i:成员收益;
URk:零售商效用;
λR:零售商的收益预期系数,等于零售商的预期收益与供应链收益的比值,0<λR<1;
决策变量:
qk:零售商的订货量
其中,i=S,R,C分别表示供应商,零售商和系统的收益;k=p,r分别表示零售商感知过程公平,结果公平。
当零售商具有公平感时,其随机效用函数为:
UR=∏R-α(λR∏C-∏R)+-β(∏R-λR∏C)+
(1)
其中,若零售商具有双边公平感,则当其收益高于预期收益时会产生愧疚感,因此β>0,但其愧疚感小于其收益低于预期收益时的愤怒感,即β<α;若零售商具有单边公平感,则当其收益高于预期收益时不会产生愧疚感甚至会产生愉悦感,因此β0,但其愉悦感要低于其愤怒感,即-α≤β。
零售商对于收益的公平关注有两种表现形式:第一种为过程公平,零售商关注比较每个随机状态的收益,其期望效用为:
EURp=E[∏R-α(λR∏C-∏R)+-β(∏R-λR∏C)+]
(2)
第二种为结果公平,零售商关注比较在反复交易中均衡结果,其期望效用为:
EURr=E∏R-α(λRE∏C-E∏R)+-β(E∏R-λRE∏C)+
(3)
基于上述假设和参数范围,本文中研究的公平类型及效用函数汇总如表1所示。

表1 公平类型
2.2 基本模型
分散控制系统中,当零售商不具有公平感时,其收益为:
∏R=pmin(x,q)-qw
(4)
集中控制时系统收益为,
∏C=∏R+∏S=pmin(q,x)-qc
(5)
3 批发价合同下具有双边公平感零售商的订购决策
批发价合同下,供应商确定批发价,零售商在需求实现之前确定订货量,零售商向供应商支付单位产品批发价,需求实现后双方收益实现,零售商和系统收益分别为式(4)和(5),具有公平感零售商的效用函数为式(1)。
3.1 关注过程双边公平零售商订购决策
关注过程双边公平的零售商的期望效用函数为式(2),有如下命题。
命题1:给定批发价合同,关注过程双边公平的零售商最优订货策略为:
其中,
qp1=[βp(1-λR)(p-pλR-w+λRc)-p(p-w)(1-λR)]/[p2(λR-1)-α(w-λRc)2-β[p(1-λR)-w+λRc]2-2pβ(1-λR)(w-p-λRc+pλR)]
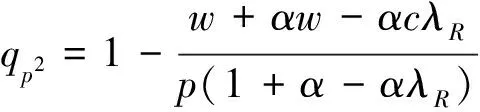
证明见附录1。
命题1直观解释为,若供应商设定较低批发价,则零售商产生的不公平厌恶与实现的需求大小相关;若供应商设定较高批发价时,零售商总认为其实际收益总是小于其预期收益,因此零售商只存在不利不公平厌恶;若供应商设定非常高批发价时,零售商的不利不公平厌恶使得其效用变为零甚至为负,此时零售商选择不订货。
记M1=p2βλR(w-c)(λR-1)+(p-w)(α+β)(w-cλR)2,根据命题1,有如下推论。
推论1:相对于不具有公平感的零售商,关注过程双边公平零售商的订货量满足:
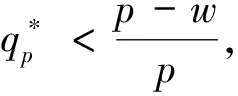
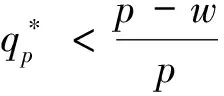
证明见附录2。
推论1直观解释为,分散控制供应链系统中,首先,当批发价较低时,关注过程双边公平的零售商的订货量与不关注公平的零售商订货量大小关系与零售商的不公平厌恶系数相关。其次,当批发价较高时,关注过程双边公平的零售商认为自己在系统中受到了不公平对待,减少订购量来惩罚供应商,因此其订货量总是小于不具有公平感零售商的订货量。
接下来,分析零售商的过程双边公平感对成员相对收益的影响。在成员不关注公平的供应链中,零售商与供应商收益为1∶2。记:
M2={2(w-c)[p2(1-β+βλR)(λR-1)-(α+β)(w-cλR)2]}/[p3(1-β+βλR)(λR-1)-2(p-w)(α+β)(w-cλR)2-p2(w-wβ+2wβλR-cβλR)(λR-1)]
由命题1,有如下推论。
推论2:关注过程双边公平的零售商:
(1)当w≤p(1-λR)+cλR时,若M2>2,则零售商的过程双边公平感使其在系统中的相对收益比没有公平感时变得更好,若M2<2,则其过程双边公平感使其在系统中的相对收益变得更差,若M2=2,其相对收益与没有公平感时相同;
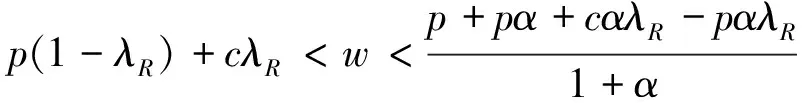
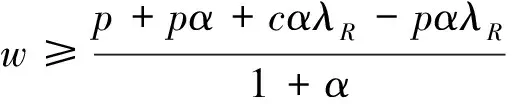
3.2 关注结果双边公平零售商的订购决策
关注结果双边公平零售商的期望效用函数为式(3),有如下命题。
命题2:给定批发价合同,关注结果双边公平零售商的最优订货策略
其中,
证明见附录3。
命题2直观解释为,当批发价很低时,零售商产生有利不公平厌恶,增加订货量,牺牲自己的收益回报供应商;当批发价处于某一特定区间时,零售商认为此时的收益总是公平的,其订货决策与公平感无关;当批发价很高时,零售商产生不利不公平厌恶,通过减少订货量牺牲自己的收益来惩罚供应商规避不公平感。
命题2不同于命题1之处为:存在一个合理的批发价区间,当批发价处于该区间时,关注结果双边公平的零售商认为是此时的收益是公平的,其订货量与公平感无关。
由命题2,可得如下推论。
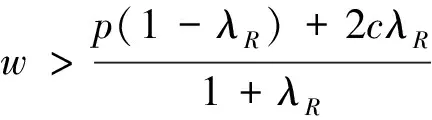
推论3由关注结果双边公平零售商的最优订货策略与不具有公平感的零售商的最优订货策略比较可以得到。推论3表明,零售商对结果双边公平的关注会影响系统及自身收益。当批发价较低时,关注结果双边公平的零售商认为自己在系统中遭受到了有利不公平,通过增加订购量来规避有利不公平,其订购决策提高了顾客服务率;当批发价较高时,关注结果双边公平的零售商认为自己在系统中遭受到了不利不公平,通过减少订购量来规避不利不公平。
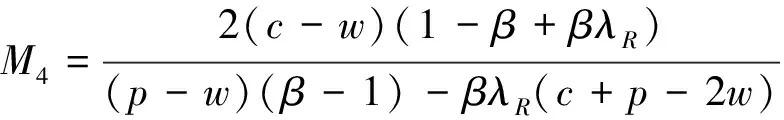
推论4:关注结果双边公平的零售商:
(1)当w
(2)当w1≤w
(3)当w2w
(4)当w≥w3时,其结果双边公平感使得双方收益均为0。
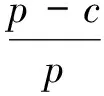
由命题3知在批发价合同下具有双边公平感的零售商并不能协调系统,不同于Cui Haitao等[17]研究结果:当零售商的双边公平感知满足特定条件时,批发价合同可以协调系统。
给定批发价合同,对比零售商在两种不同双边公平关注方式下的最优订货量,记:
T1=-p2(1-λR)2[(w-p)(β-1)+(p-c)βλR]-2(p-pλR-w+cλR)[p2(λR-1)(1+βλR-β)-(α+β)(w-cλR)2]
T2=(α+β)(w-p+pλR-cλR)[w2(1+α)-wλR(c+p+2cα)+cλR(p+cαλR)]
有如下命题。
命题4:具有双边公平感的零售商的订购决策有如下性质:
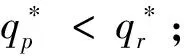
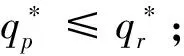
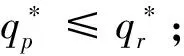
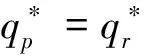
证明见附录4。
命题4直观解释为,当批发价较低时,关注结果双边公平的零售商,其订货量总是大于关注过程双边公平的;当批发价处于合理的水平时,两种公平关注形式下的订货量相对大小取决于零售商的不公平厌恶程度;当批发价较高时,零售商的双边公平关注形式不影响其订购决策。
4 批发价合同下具有单边公平感零售商的订购决策
当零售商为关注单边公平时,有如下说明。
说明1:(1)关注过程单边公平的零售商,其最优订货策略同关注过程双边公平的,最优订货策略同命题1;
(2)关注过程单边公平的零售商,其公平感对自身在系统中相对收益的影响同关注过程双边公平的,其影响同推论2;
(3)关注结果单边公平的零售商,其最优订货策略同关注结果双边公平的,最优订货策略同命题2;
(4)关注结果单边公平的零售商,其公平感对自身在系统中相对收益的影响同关注结果双边公平的,其影响同推论4。
由说明1,可知两种单边公平关注方式下的最优订货量关系同命题4。
证明见附录5。
推论5不同于推论2,关注过程单边公平零售商的最优订货量总是小于不具有公平感的零售商,公平感知会损害自身收益和系统收益。
当零售商为关注结果单边公平,有如下说明。
推论6:关注结果单边公平的零售商的最优订购量满足:
(1)当w 将关注结果单边公平的零售商的最优订购量同(p-w)/p比较即可得推论6。推论6直观解释为,若零售商是关注结果单边公平的,当批发价过低时,零售商会高估自身收益所带来的愉悦感,因此,零售商选择较小订购量,就获得较大效用;当批发价处于合适水平时,零售商的公平感会减缓系统中的“双重加价”效应,促进系统成员间的协调;当批发价过高时,零售商认为是不公平的,会选择减少订货量,规避不公平。 命题5:两种单边公平关注方式的零售商的订货量总是小于(p-c)/p。 证明见附录6。 命题5的直观解释为,当零售商是具有单边公平感的,两种公平关注方式的零售商订购决策都不能协调系统。 本文对由一个供应商一个零售商组成的供应链系统进行了分析,其中市场需求为[0,1]上的均匀分布。分别研究了不同类型公平感的零售商在批发价合同中的订购决策。首先研究了当零售商具有双边公平感时,公平感对订购决策的影响。两种公平关注方式的零售商均不能协调系统;两种公平关注方式的零售商其订购决策对于系统收益的影响取决于批发价及公平关注的程度。最后,研究了当零售商具有单边公平感时,公平感对订购决策的影响。两种公平关注方式的零售商均不能协调系统;关注过程公平的零售商,其订购决策使得系统状况变差;关注结果公平的零售商,其订购决策对于系统收益的影响取决于批发价及公平关注的程度。 未来研究方向:(1)本文只考虑了零售商的公平感对于供应链的影响,可进一步研究当供应商、零售商均有公平感时,其对供应链的影响;(2)本文只研究了批发价合同中具有公平感的零售商订购决策,未来可研究在其他合同中,如数量折扣、收益共享、销售返利合同,数量柔性合同等,供应链成员的公平感对其决策行为的影响;(3)本文中假设两种公平关注方式是独立存在的,可研究两种公平关注方式同时存在时对供应链成员决策的影响。 附录: 附录1:命题1证明 对于关注过程双边公平的零售商 ,其效用函数为: UR=∏R-α(λR∏C-∏B)+-β(∏R-λR∏C)+ =pmin(x,q)-qw-α[(λR-1)pmin(q,x)+qw-λRqc]+ -β[(1-λR)pmin(q,x)-qw+λRqc]+ 其中, (λR-1)pmin(q,x)+qw-λRqc= 关注过程双边公平零售商的期望效用函数为, EURP=E[∏R-α(λR∏C-∏R)+-β(∏R-λR∏C)+] (1)当w≤p(1-λR)+λRC时 给定w,零售商最大化自己的期望效用,EURp1为关于q的凹函数,可得一阶导数为零时对应的订货量为: qp1=βp(1-λR)(p-pλR-w+λRc)-p(p-w)(1-λR)/{p2(λR-1)-α(w-λRc)2-β[p(1-λR)-w+λR)c]2-2pβ(1-λR)(w-p-λRc+pλR)} (2) 当w>p(1-λR)+λRc时: 给定w,关注过程双边公平的零售商最大化自己的期望效用,EURp2为关于q的凹函数,可得倒数一阶导数为零的点所对应的订货量为: 由(1)和(2)可得在给定批发价w时,零售商的最优订单量。 证明完毕。 附录2:推论1证明 综上,推论1得证。 证明完毕 附录3:命题2证明 证明:关注结果双边公平的零售商的效用函数为: UR=∏R-α(λR∏C-∏B)+-β(∏R-λR∏C)+ 其期望效用函数为: EURp=E∏R-α(λRE∏C-E∏R)+-β(E∏R-λRE∏C)+ (1)若w 其中 (2)若w≥p(1-λR)+cλR,则有,EURr=EURr1,q≥0。 综上可得最优订货量为: 证明完毕。 附录4:命题4证明 (1)当w (2)当w1≤w (3)当w2≤w≤p(1-λR)+cλR时, 记M5=p(1+α-αλR)[p2(1+βλR-β)(λR-1)-(α+β)(w-cλR)2], T2=(α+β)(w-p+pλR-cλR)[w2(1+α)-wλR(c+p+2cα)+cλR(p+cαλR)],其中M5<0。 命题得证。 证明完毕。 附录5:推论5证明 显而易得,p3(1-λR)(β-1-βλR)-p(α+β)(w-λRc)2<0, 证明完毕。 附录6:命题5证明 证明:(1)当w 当-α≤β≤0时,p(1-β+βλR)[p2(1+βλR-β)(λR-1)-(α+β)(w-cλR)2]<0 命题得证。 证明完毕。 参考文献: [1] Guth W, Schmittberger R, Schwarze B.An experimental analysis of ultimatum bargaining[J].Journal of Economic Behavior & Organization, 1982, 4(3): 367-388. [2] Berg J, Dickaut J, McCabe K.Trust, reciprocity and social history[J].Games and Economic Behavior, 1995, 10: 122-42. [3] Kahneman D, Knetsch J L, Thaler R H.Fairness and the assumptions of economics[J].Journal of Business, 1986, 59: 285-300. [4] 每台ipad苹果劲赚150美元,中国工人工资仅8美元[EB/OL].[2012-02-15].环球网:http://www.huanqiu.com/roll/2012-02/2440233.html. [5] Fehr E, Schmidt K M.A theory of fairness, competition and cooperation[J].Quarterly Journal of Economics, 1999,114: 817-868. [6] Bolton G E, Ockenfels A.ERC: A theory of equity, reciprocity, and competition[J].The American Economic Review, 2000, 90(1): 166-193. [7] Charness G, Rabin M.Understanding social preferences with simple tests[J].Quarterly Journal of Economics, 2002,117(3): 817-869. [8] Loch C H, Wu Yaozhong.Social preferences and supply chain performance: An experimental study[J].Management Science, 2008, 54(11): 1835-1849. [9] Pavlov V, Katok E.Fairness and coordination failures in supply chain[R].Working paper, The Pennsylvania State University,2010. [10] Thibaut J W, Walker L.Procedural justice: A psychological analysis[M].New York: L.Erbaum Associates, 1975. [11] Lind E A, Tyler T R.The social psychology of procedural justice[M].New York: Plenum Press, 1988. [12] Tyler T R, Blader S L.The group-engagement model: procedural justice, social dentity, and cooperative behavior[J].Personality and Social Psychology Review, 2003,7(4): 349-361. [13] McFarlin D B, Sweeney P D.Distributive and procedural justice as predictors of satisfaction with personal and organizational outcomes[J].Academy of Management Journal, 1992, 35 (3): 626 - 637. [14] Camerer C F, Ho T H, Chong J K.Behavioral game theory: thinking, learning and teaching[R].Working paper, National University of Singapore,2001. [15] Kahneman D.Maps of bounded rationality: Psychology for behavioral economics[J].The American Economic Review, 2003, 93(5): 1449-1475. [16] Luong H T, Phien N H.Measure of bullwhip effect in supply chains: The case of high order autoregressive demand process[J].European Journal of Operational Research, 2007,183(1): 197-209. [17] Cui Haitao, Raju J S, Zhang Z J.Faireness and channel coordination[J].Management Science, 2007, 53(8):1303-1314. [18] Ozgun C D, Chen Youhua Jianbin, Li J B.Channel coordination under fairness concerns and nonlinear demand[J].European Journal of Operational Research, 2010, 207(1): 1321-1326. [19] Chen J G, Hu Q Y, Song J S.Altruism and supply chain performance[R].Working paper, Duke University,2012. [20] Rotemberg J J.Human relations in the workplace[J].Journal of Political Economy, 1994,102(4): 684-717. [21] Wu Xiaole, Niederhoff J.Fairness in selling to the newsvendor[R].Working paper, Fudan University,2012. [22] 杜少甫, 杜婵, 梁樑, 等.考虑公平关切的供应链契约与协调[J].管理科学学报,2010, 13(11): 41-48. [23] Karlin S.Total positivity[M].Catifornia:Stanford University Press,1968. [24] Anupindi R, Bassok Y, Zemel E.A general framework for the study of decentralized distribution[J].Manufacturing Service operations management, 2001,3(4):340-368. [25] Schweitzer M E, Cachon G P.Decision bias in the newsvendor problem with a known demand distribution: Experimental evidence[J].Management Science, 2000,46(3):404-420. [26] Macneil I R.The new social contract: An inquiry into modern contractual relations[M].New Haven,CT:Yale University Press,1980. [27] Frazier G L.Interorganizational exchange behavior in marketing channels: A broadened perspective[J].Marketing, 1983,47(4):68-78.
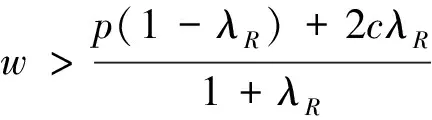
5 结语