基于知识元的突发事件风险分析

卢小丽，于海峰

(1.大连理工大学管理与经济学部，辽宁 大连 116024；2.大唐国际核电有限公司，辽宁 大连 116010)

1 引言

近年来，各种突发事件频繁发生给人类生产生活带来极大的影响。由突发事件引发的连锁反应激发诸多社会问题，严重地威胁着人类社会和谐发展。风险分析是突发事件应急管理中的一项复杂而重要的工作，科学的分析突发事件的风险，有利于应急管理部门科学制定应对方案，采取有效措施预防突发事件发生、控制突发事件发展、降低突发事件损失。由于人类认知的局限性和客观世界的复杂性，应急管理的决策不可避免地受到各类不确定因素的影响。在突发事件发生前，利用已认知的相关因素对突发事件风险进行分析和预测，对增强社会抗灾防灾能力，提高社会抵御突发事件风险能力具有十分重要的现实意义。突发事件演化过程的影响因素多，实时观测样本数据少且维数高，风险信息不完备等导致很难获得可靠的突发事件风险分析结果，多因素的综合风险评估理论与方法已成为应急管理中的关键科学问题之一[1]。

突发事件风险具有极高的随机不确定性，尽管已有学者从不同视角来分析突发事件的风险[2-7]，但突发事件影响因素多、观测样本的不足导致其风险分析结果的可靠性和科学性无法保证。由于突发事件往往是多因素相互作用引发的，单因素又无法全面反映事件发生机理和发展过程。为解决风险分析中多因素的数据处理问题，一些学者将投影寻踪方法应用于突发事件风险分析[8-9]。投影寻踪方法将高维数据向低维空间投影，并通过分析低维空间的投影特性来研究高维数据的特征。该方法解决了多因素高维数据的降维问题，但当观测样本数据少时，投影到一维空间的数据信息量不够，无法全面识别突发事件的风险。针对小样本提供信息不充分、数据不全面的问题，一些学者引入信息扩散理论研究突发事件风险[10-12]。信息扩散理论通过选取适当的扩散函数，将单因素样本信息扩散到指标论域中所有控制点，弥补了突发事件样本不足的缺陷，但仍无法解决风险分析样本维数高的难题。

可见，无论是采用投影寻踪方法还是信息扩散理论来研究突发事件的风险都存在着不足，如何结合两种分析方法的优势，克服突发事件风险分析中的多因素高维数据和小样本数据信息不完备的约束，对突发事件风险进行科学的评估成为突发事件风险分析的关键。目前，鲜有文献将投影寻踪方法和信息扩散理论相结合研究突发事件的风险。鉴于此，本文在投影寻踪方法和信息扩散理论的基础上，提出基于知识元的突发事件风险分析方法。该方法利用对各类突发事件已认知的知识要素描述事件的共性本体特征，建立突发事件知识元模型，明确输入属性状态集和输出属性状态集，获取知识元要素观测数据；采用投影寻踪方法对突发事件的多因素进行降维，将事件高维输入属性值投影到一维子空间，获得一维投影特征值，以此单因素反映多因素的数据特征；利用信息扩散理论解决单因素风险扩散问题，将输入属性的投影特征值扩散到输出属性的风险指标论域的控制点上，从而确定突发事件发生的可能性。

2 突发事件知识元描述

突发事件是受时空条件约束的诸多耦合因素相互作用的复杂系统，具有一定的结构并表现出特定的行为[13]。突发事件结构体现了系统要素及其相互作用关系，其行为包括系统的状态和变化过程。突发事件知识元正是在突发事件系统观点的框架下，从事件状态及引发这一状态突变的要素出发，包含突发事件所应有的基本结构要素和行为要素的最小基本单元。

王延章[14]教授系统地提出了一个模型管理的共性知识体系，建立了相应的知识元模型。本文对该模型进行了扩展并应用于突发事件研究领域，利用知识元模型描述突发事件，如式1所示：

Km=(Nm,Am,Rm)

(1)

式中，Nm为事件知识元概念或属性名，Am表示对应的属性状态集，Rm表示Am×Am上的映射关系集，描述了属性状态变化及相互作用关系。

设a∈Am，属性状态对应的知识元：

Ka=(pa,da,fa)

(2)

式中，pa为可测性特征描述，da为测度量纲，fa为关系规则。

设r(r∈Rm)为Am×Am上的一个映射关系，属性映射关系对应的知识元：

(3)

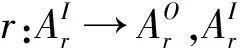
3 突发事件风险分析模型

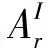
图1 突发事件知识元风险分析模型输入输出属性状态集映射关系

突发事件风险分析模型包括以下四个步骤。

步骤1：突发事件知识元描述。

步骤2：知识元输入元素样本数据预处理。

步骤3：知识元输入元素样本数据降维。

(1)寻找最佳投影方向

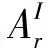
Q(α)=SZ·DZ

(4)

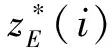
(5)

(6)

(7)

(8)

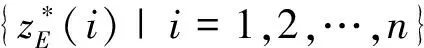
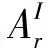
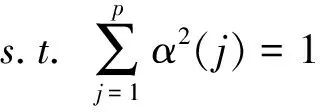
(9)

这是一个以{α(j)|j=1,2,…,g}为优化变量的复杂非线性优化问题，本文采用基于实数编码的加速遗传算法(Real Coding based on Accelerating Genetic Algorithm，简称RAGA )解决全局优化问题。

(2)风险等级标准降维

(10)

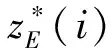
(3)观测样本数据降维

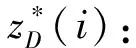
(11)

步骤4：知识元输入元素风险信息向输出扩散。

(1)风险信息扩散

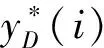
(12)

k=1,2,…,w，i=1,2,…,n

式中，h为扩散系数，由样本集中样本最大值b、最小值a和样本个数n确定。

(13)

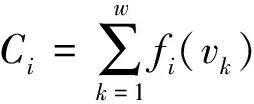
(14)

(15)

(2)风险概率估算

令

(16)

H表示vk各点上的样本数的总和，将样本落在vk处的频率值作为概率的估计值p(vk)：

p(vk)=h(vk)/H

(17)

超越vk的概率估计记为P(v≥vk)，即所要求的风险概率估计值：

(18)

4 实例分析

虽然突发事件的触发机理、事件性质和演化过程各不相同，导致不同突发事件表现出来的个性特征存在着很大差异。但大量具体领域突发事件研究表明，不同突发事件又存在一定的共性规律。若将突发事件看作一个系统，则突发事件发生发展的共性规律可描述为：在系统外部环境的作用(环境输入)下，突发事件的内部状态(状态属性)发生突变，系统状态属性之间的相互作用对外部环境造成影响(输出要素)。同时，应急主体根据事件状态采取应对措施(控制输入)控制事件状态的发展，各要素之间的作用与影响共同构成了突发事件发生演化的整体行为。知识元模型不仅能够反映突发事件的共性特征，即不同类型的突发事件均具有输入属性、状态属性和输出属性；又能够扩展出不同突发事件的个性特征，即突发事件各属性的元素不同，元素的突变条件不同。因此，应用本文中的共性并可向专业个性扩展的突发事件知识元模型，可对各类突发事件进行描述。

本文以某湖泊突发水污染事件为例，说明如何建立水污染事件知识元以及水污染事件风险分析的具体过程，检验本文提出的风险分析方法的可行性和有效性。

4.1 突发水污染事件知识元属性

某湖泊突发水污染事件知识元描述如表1所示。输入元素8个，分别为氨氮(N-NH3)、五日生化需氧量(BOD5)、总磷(TP)、总氮(TN)、化学需氧量(CODCr)、溶解氧(DO)、高锰酸盐指数(CODMn)、阴离子表面活性剂(LAS)；输出元素1个，突发事件风险值。根据国家《地表水环境质量标准(GB3838-2002)》，建立水污染风险等级标准，如表2所示。湖泊水污染风险等级标准为5级，每级标准对应8个输入元素，属于5组8维数据。湖泊8个监测点实时检测数据[18]如表3所示。

表1 突发湖泊水污染事件知识元描述

表2 水污染风险等级标准

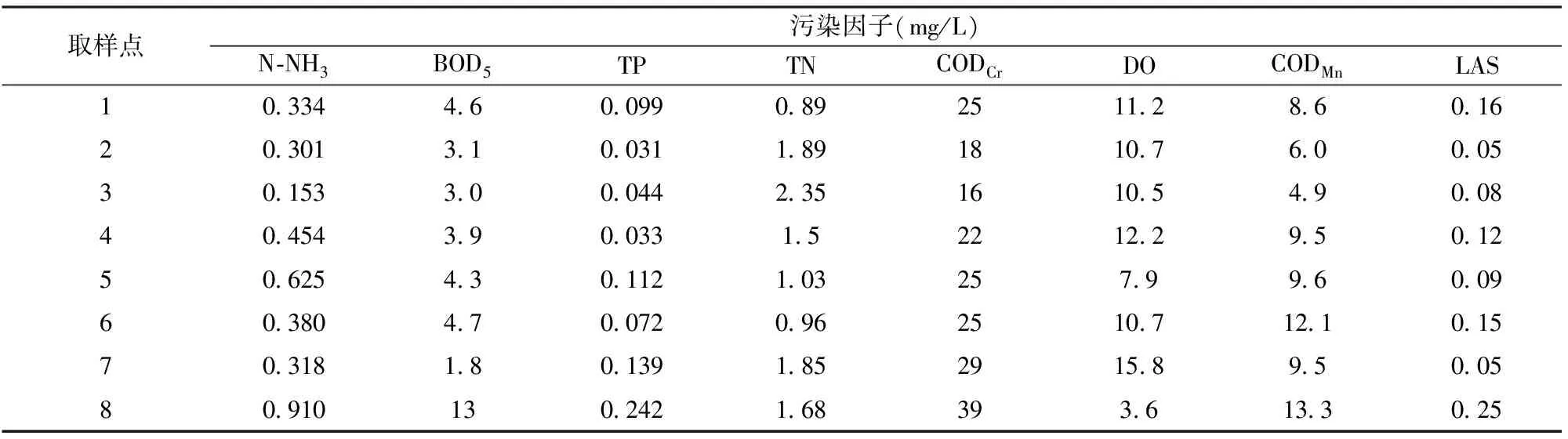
表3 某湖泊监测点观测数据

4.2 突发水污染事件风险概率

对表2、表3数据进行归一化处理，采用本文提出的突发事件风险分析模型，计算该湖泊水污染事件风险概率估计值。

(1)最佳投影方向

对表2中湖泊水污染等级标准的样本进行投影寻踪，寻找最佳投影方向。本文采用RAGA优化方法，选定父代初始种群规模为n=400，交叉概率pc=0.80，变异概率pm=0.05，优秀个体数目选定为50个，加速次数为7，得出最佳投影方向α*=(0.3094，0.4004，0.2765，0.4046，0.3809，0.3284，0.2908，0.4078)。

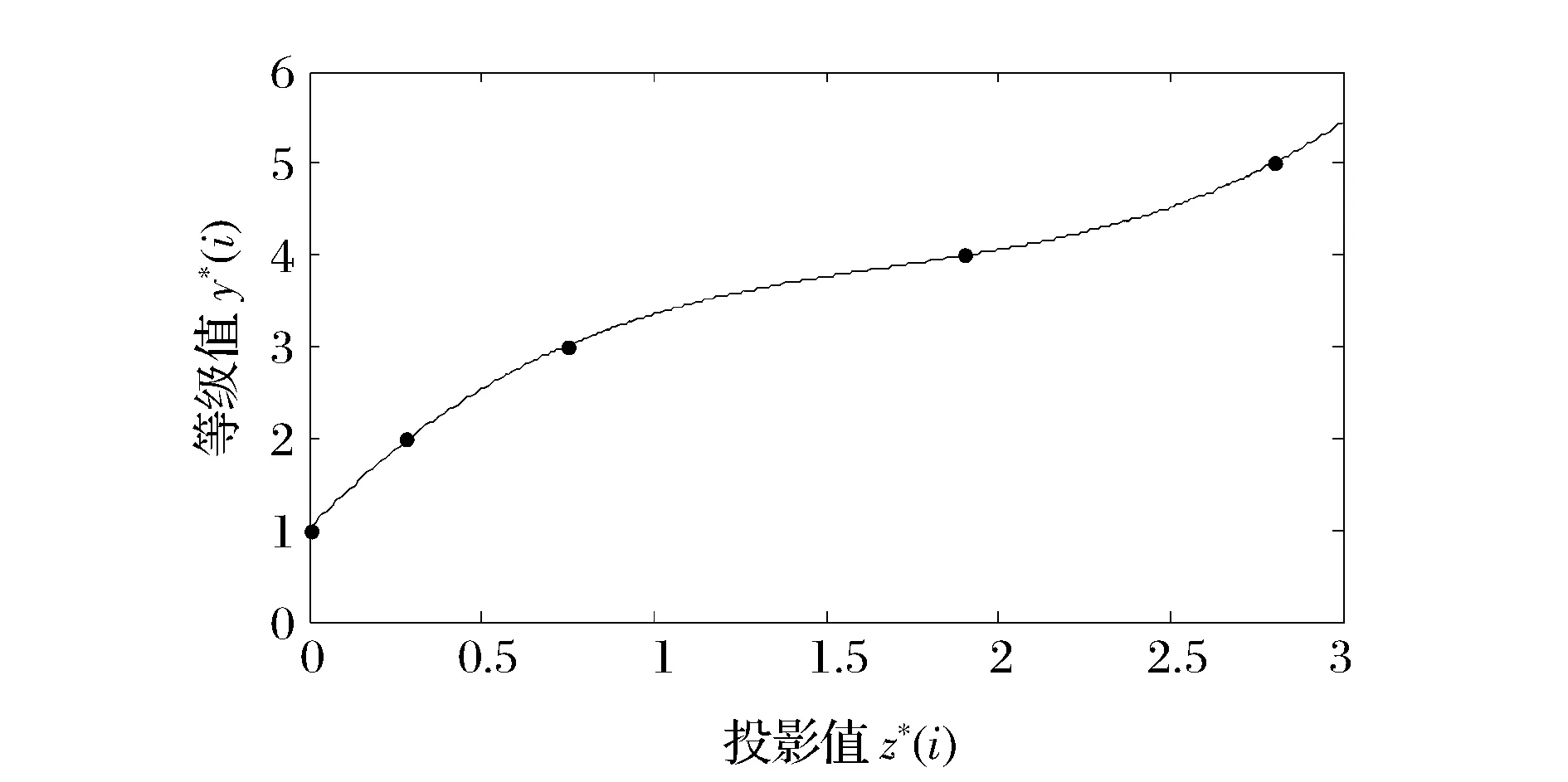
图2 水污染风险等级值与投影值关系图

(2)风险等级标准降维

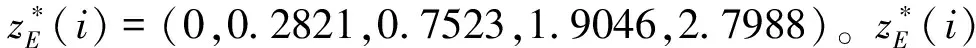
y*=0.3885(z*)3-1.985(z*)2+3.9378(z*)+1.0124

(19)

对该模型进行检验，模型R2=0.9998，误差分析如表4所示，平均绝对误差为0.0121，平均相对误差为0.65%，该结果表明模型拟合程度好，检验结果显著。

表4 水污染风险等级标准投影寻踪误差分析表

(3)观测样本数据降维

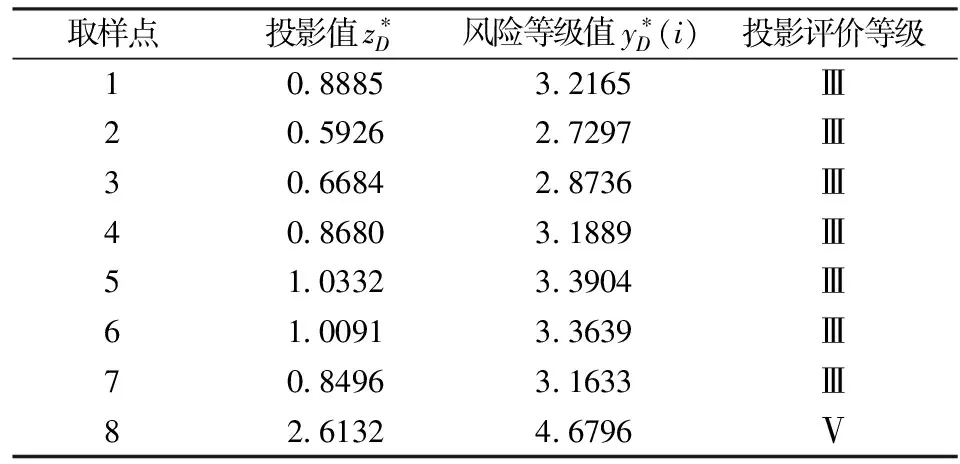
表5 某湖泊水污染观测数据一维投影值和风险等级值

(4)知识元输入元素风险信息向输出扩散

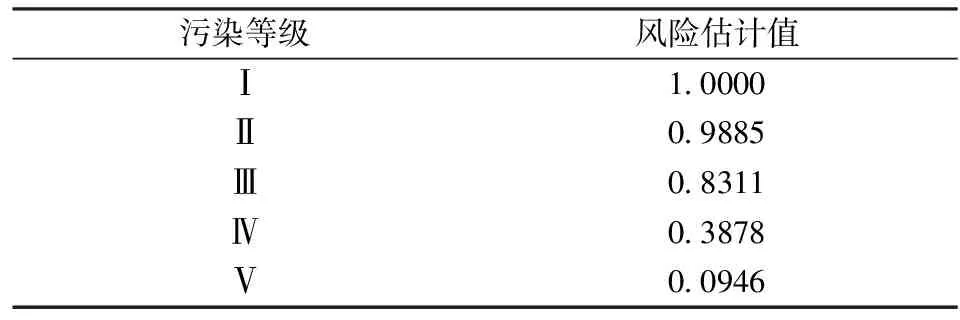
表6 某湖泊水污染风险概率估计值

4.3 突发水污染事件风险分析

(1)各样本点水污染等级分析

由表5可知，样本点8的水污染等级为Ⅴ级，其余样本点的水污染等级均为Ⅲ级。可见，样本点8的水污染最严重。环境管理部门需要对水污染严重水域采取及时的治理措施，降低污染等级，以提高湖泊整体水质。

(2)水污染因子影响程度分析

最佳投影方向各分量的大小实质上反映了各水污染指标对水污染等级的影响程度，值越大则对应的水污染指标对水污染等级的影响程度越大。该湖泊水污染的最佳投影方向α*=(0.3094，0.4004，0.2765，0.4046，0.3809，0.3284，0.2908，0.4078)，该结果表明，水污染事件输入元素对水污染等级的影响程度依次为：LAS >TN >BOD5>CODCr>DO>N-NH3>CODMn>TP，管理者可依据该结果，进一步检验湖泊原水污染评价标准的合理性。

(3)不同程度污染的风险分布

从表6可知，该湖泊水污染风险等级为Ⅰ、Ⅱ、Ⅲ、Ⅳ的概率分别为1.0000、0.9885、0.8311、0.3878。此结果表明，根据本次监测数据判断该湖泊水污染处于低风险的概率较高，即该湖泊突发水污染事件的危险比较低。同时，由于风险等级为Ⅴ的发生概率为0.0946，此结果表明，尽管该湖泊在本次监测中处于安全状态，但如果对该湖泊的主要污染物缺少必要的控制和监控机制，也会存在一定的概率导致该湖泊突发水污染事件。

5 结语

为解决突发事件影响因素多、样本数据少且维数高导致风险信息不完备、风险分析结果不稳定的问题，本文将投影寻踪方法与信息扩散理论巧妙地结合，提出了一种以突发事件知识元为基础的风险分析方法。该方法采用知识元模型描述了突发事件已认知的共性本体特征，利用投影寻踪方法获得了输入元素风险等级标准数据的最佳投影方向，降低了输入元素观测样本的维数，应用信息扩散理论将输入元素观测样本一维投影特征值所包含的风险在输出属性的风险指标论域的控制点上进行信息分配，从而确定了突发事件发生的风险概率。并以某湖泊水污染事件为例，对提出的风险分析方法进行实例检验。实例分析结果表明本文提出的突发事件风险分析方法能够根据湖泊水污染风险等级标准和观测点的样本数据，对研究区域突发事件风险概率进行动态定量的分析和评估。因而可利用本文提出的风险分析方法，在突发事件发生前利用事件相关因素分析发生的可能性，预测事件发生的风险，辅助决策者及时采取必要措施控制事件发展，降低事件带来的损失。

在建立风险分析模型过程中，本文与采用先“信息扩散理论”后“投影寻踪方法”的计算步骤[19]进行了对比研究。如果采用后者，需要对输入属性状态集中每个元素进行信息扩散，再利用投影寻踪方法对多维数据进行降维，风险评估的计算量会随着输入属性状态集中元素的数量增加而变得越来越大。本文采用先“投影寻踪方法”后“信息扩散理论”的计算步骤，投影寻踪和信息扩散各需计算一次，不仅提高了计算效率同时也提升了计算精度。此外，突发事件受到多因素共同作用，在对事件进行风险分析过程中，首先需要解决多因素问题，因此选择投影寻踪方法将多因素转化为单因素；再运用信息扩散理论将单因素的风险信息扩散到风险指标论域。即本文先采用投影寻踪方法后采用信息扩散理论的分析步骤是非常符合问题分析的逻辑性。因此，针对突发事件风险分析的研究，无论从计算效率还是从问题分析逻辑上，采用“先投影寻踪方法后信息扩散理论”都明显优于“先信息扩散理论后投影寻踪方法”。

参考文献：

[1] 范维澄.国家突发公共事件应急管理中科学问题的思考和建议[J].中国科学基金，2007,(2)：71-76.

[2] Guzzetti F, Reichenbach P, Ardizzone F, et al.Estimating the quality of landslide susceptibility models [J].Geomorphology, 2006, 81(1/2): 166-184.

[3] Guikema S D.Natural disaster risk analysis for critical infrastructure systems: An approach based on statistical learning theory [J].Reliability Engineering and System Safety, 2009, 94(4): 885-860.

[4] Iliadis L S，Spartalis S I.Fundamental fuzzy relation concepts of a D.S.S.for the estimation of natural disasters' risk [J].Mathematical and Computer Modelling, 2005, 42(7): 747-758.

[5] Liu Hexiang, Zhang Dalin.Analysis and prediction of hazard risks caused by tropical cyclones in Southern China with fuzzy mathematical and grey models [J].Applied Mathematical Modeling, 2012, 36(2): 626-637.

[6] 王文圣，金菊良，李跃清.基于集对分析的自然灾害风险度综合评价研究[J].四川大学学报(工程科学版)，2009，41(6)：6-12.

[7] 吴益平，唐辉明，葛修润.BP模型在区域滑坡灾害风险预测中的应用[J].岩土力学，2005，26(9)：1409-1413.

[8] 金菊良，张欣莉，丁晶.评估洪水灾情等级的投影寻踪模型[J].系统工程理论与实践，2002，22(2)：140-144.

[9] Wang Shunjiu, Zhang Xinli, Yang Zhifeng, et al.Projection pursuit cluster model based on genetic algorithm and its application in karstic water pollution evaluation[J].International Journal of Environment and Pollution, 2006, 28(34): 253-260.

[10] Huang Chongfu.Principle of information diffusion[J].Fuzzy Sets and Systems, 1997, 91(1): 69-90.

[11] Liu Xingpeng, Zhang Jiquan, Cai Weiying, et al.Information diffusion-based spatio-temporal risk analysis of grassland fire disaster in northern China[J].Knowledge-Based Systems, 2010, 23(1): 53-60.

[12] 王洪德，郑玉钱.基于网格划分及信息扩散的化工园区安全风险评价技术[J].系统工程理论与实践，2010，30(7)：1286-1292.

[13] 裘江南，师花艳，叶鑫，等.基于事件的定性知识表示模型[J].系统工程，2009，27(10)：1-8.

[14] 王延章.模型管理的知识及其表示方法[J].系统工程学报，2011，26(6)：850-856.

[15] Friedman J H, Tukey J W.A projection pursuit algorithm for exploratory data analysis[J].IEEE Trans on Computer, 1974, C-23(9): 881-890.

[16] 付强，赵小勇.投影寻踪模型原理及其应用[M].北京：科学出版社，2006.

[17] 黄崇福.自然灾害风险评价一理论与实践[M].北京：科学出版社，2005.

[18] 李凤超，刘存歧，管越强，等.应用多元分析方法评价白洋淀水质现状[J].河北大学学报(自然科学版)，2006，26(4)：405-410.

[19] 余航，王龙，田琳,等.基于信息扩散理论的云南农业旱灾风险评估[J].中国农村水利水电，2011，12：91-94.