信息可信与贷款利率确定问题的供应链鲁棒模型分析

于 辉，刘鹏飞，孙彩虹

(1.重庆大学经济与工商管理学院，重庆 400030；2.重庆大学现代物流重庆市重点实验室，重庆 400044)

1 引言

众所周知，面对不同企业，银行有不同的贷款政策。亨通集团崔根良曾就这一问题发表个人观点，称银行放给大企业一般是基准利率，放给大多数一般企业时在基准利率的基础上还要上浮，上浮的幅度是20%或者30%，企业贷款以后还要求存款，有的甚至要存50%[1]。2011年08月16日，第一财经日报称在江苏近150万户的企业总数中，不到0.6%的大企业获得了60%的信贷资源，贷款的集中度越来越高，而一般企业的贷款仍然寥寥[2]。大企业实力雄厚，信用度高，这使得银行充分信任他们以至于愿意以较低利率提供适量贷款给他们。现实生活中，存在部分企业为获得银行贷款而提供夸大甚至虚假的信息，这让银行在接受贷款申请时颇为谨慎。作为营利性质的企业，银行自然会考虑风险和收益，考虑相信哪些信息，进而决定贷款利率是非常现实的做法。这样的结果是银行区别对待不同企业，致使贷款结构不合理，对多数企业的日常运营造成重大影响，进而对供应链的运作产生一定的影响。

供应链的出现改变了银企之间一对一的关系。过去银行放贷时考虑的是企业能否还款，供应链出现以后，链上企业战略性合作极为密切，利益关系往往是牵一发而动全身，银行放贷时考虑更多的是整体供应链的运营状况，供应链金融的出现便是积极的回应。在对资金流要求越来越高的现代企业中，企业缺乏资金，向银行借贷是经常发生的事情，一旦借贷，则借贷成本又是企业必须考虑的问题。所以借贷政策是银行和企业必须考虑的重要因素。

学者已经对企业运营或金融服务做过众多研究，例如企业运营中的EOQ模型、(s,S)和(Q,r)随机库存模型、多项目供应链、MRP模型以及JIT模型等[3-8]，然而资金充足是上述研究的基本假设。同样，金融服务的研究相对较多，例如Modigliani和Miller[9]的MM定理。Brealey和Mayers[10]的研究描述了公司融资的理论与实践等等。

关于二者相互协调的研究却是近几年才发展起来的。Buzacott和Zhang[11]首次将基于资产的融资引入生产决策中并建立了相关模型，针对市场需求的不确定性，研究了基于资产的融资业务下的订货和利率决策问题。Xu Xiaodong和Birge[12]论述了资金约束问题如何影响企业的生产决策。Hu Qiaohai和Sobiel[13]应用多周期报童模型研究了企业资本结构和运营决策之间的相互作用。Boyabatli和Toktay[14]分析了不完全信息的融资市场对企业金融和运营决策的影响。Data和Hu Qiaohai[15]在Buzacott和Zhang[11]等研究的基础上，假定利率内生和资金使用成本不是固定的无风险利率，且令银行为领导者，零售商为追随者进行Stackelberg博弈，得出了最优的订货和利率，并分析表明非线性借贷策略可以有效协调渠道收益。Caldentey[16]等考虑利用金融市场来缓解零售商的资金约束，研究了三类合同(柔性合同、批发合同和对冲柔性合同)，并比较了不同合同下供应链的绩效。

国内学者近几年在这方面也进行了较为深入的研究，陈祥锋等[17]研究了零售商从追求风险中性的资本市场获得融资服务以实现自身最优采购时，供应链中金融和运营的综合决策问题。庞素琳[18]在考虑拖欠还款概率存在的影响下，建立了信贷风险决策模型，给出了相应的信贷风险决策机制。钟远光[19]等研究了零售商初始资金不足时，如何借助外部的融资政策做出最优的订货与定价决策。

以上研究多数的基本假定是银行相信企业提供的全部信息。然而，金融机构的现行做法大多并不是这样，通常他们只相信融资企业提供的部分信息，通过部分信息进行贷款决策。

本文将银行利率决策所依据的信息作为切入点，把该信息分为银行全部相信和银行部分相信两种情形。用已知需求分布刻画全部可信的情形(常规情形)，用已知均值和方差刻画部分信息可信的情形(鲁棒情形)，分别构建了银行参与的由供应商和零售商组成的二级供应链模型。通过数值实例，将鲁棒情形与正常情形进行对比，分析了银行只相信部分信息的利率决策对供应链整体运营以及收益的影响。研究发现，银行采用部分信息决策并不能有效增加其收益，但其利率决策对供应链整体运作效率有非常显著的影响。为了突出研究银行利率决策对供应链运营所产生的影响，本文假定银行认为融资企业一定能够还款。

2 模型描述和基本假设

市场需求具有很大的不确定性，作为更加靠近终端市场的零售商，往往能够通过一定的途径获得相关的市场需求信息。假定零售商通过历史销售数据或者市场专家估计确定出市场的近似需求信息，零售商将该信息共享给银行作为银行决策的依据，并希望得到银行贷款。

银行收到贷款申请并获得零售商提供的全部信息，对于这些信息，理论上银行有三种处理方式：相信全部信息、相信部分信息以及全部都不相信。情形一，相信全部信息。按照假定，此时银行将以零售商提供的市场需求分布信息进行决策。情形二，相信部分信息。虽然零售商更加靠近终端市场，对市场信息的掌控、预测更加全面一些。但是，出于自身利益的考虑，零售商可能会提供一些夸大甚至虚假的信息。如果银行没有任何信息过滤而全部相信零售商提供的信息，自身很有可能承受较大的风险，所以银行有选择性的相信零售商提供的部分信息也是一种可能的做法。假定银行相信部分信息，以零售商提供的市场需求的均值和方差信息为依据进行决策。情形三，全部都不相信。此时将不发生借贷关系，这里不予考虑。

零售商和银行在上述两种情形下进行Stackelberg博弈。银行作为“领导者”，清晰的知道零售商的决策过程，首先确定出合适的利率。零售商作为追随者，在给定的利率下，确定出订货量，同时也确定出了贷款金额。待零售商以固定零售价格售出产品、回笼资金以后，向银行还本付息。两种情形下的具体运作流程，如图1所示。

图1 两种情形下运作流程图

基本假设：

(1)零售商缺货商誉损失为零；

(2)贷款一定会发生；

(3)供应商能够满足零售商所有的订货；

(4)零售商和银行之间信息共享，且信息对称；

(5)给定贷款利率下，零售商追求利润最大化。

(6)零售商面临的市场需求为随机变量，服从某一分布，分布函数满足递增失败率(IFR)。有关IFR的更多讨论，请参看Cachon[20]等文献。

符号说明：

c：单位产品的采购批发价格；

w：供应商单位产品的制造成本；

Q：零售商的订货量；

r：银行制定的贷款利率；

r′：借贷市场基准利率；

η：零售商的自有资金量(cQ>η)；

B：零售商的贷款额(B=cQ-η)；

p：单位产品的市场零售价格；

p>c(1+r)：资金约束的零售商有借款并还款的可能性；

s：单位剩余产品的残值(c≥s)；

D：市场对产品的需求量，为随机变量；

f(·)为市场需求的概率密度函数；

F(·)为市场需求的累积概率密度函数；

μ：市场需求的期望；

σ2：市场需求的方差。

3 全部信息可信模型

3.1 零售商订货决策

在银行给定的利率下，零售商以期望利润最大化为目标进行最优订货决策。零售商期望收益函数为：

(1)

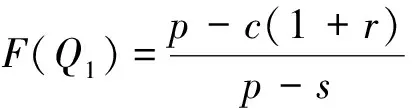
证明：对(1)式分别求一阶、二阶导数：

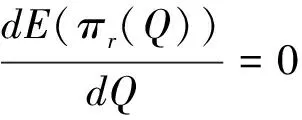
定理1得证。

3.2 银行利率决策

在该决策过程中，零售商作为追随者，订货量会随着银行的利率决策变化而变化，订货量Q1是利率r的函数，给出鲁棒的银行收益函数:

πb(r)=[c·Q(r)-η](r-r′)

(2)

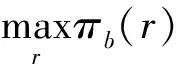
(证明见附录A)

3.3 均衡分析

命题1：全部信息可信情形下零售商和银行的Stackelberg博弈存在均衡，且均衡解为Q1*和r1*。其中Q1*、r1*分别满足以下两式：

p-(p-s)F(Q1*)-c[1+r′+

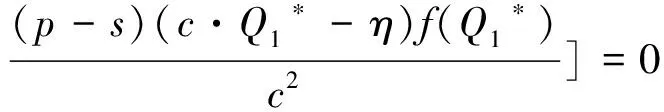
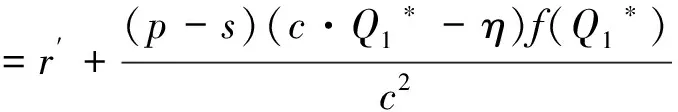
(证明见附录B)

4 部分信息可信模型

4.1 零售商订货决策

在银行给定的利率下，零售商以期望利润最大化为目标进行最优订货决策。零售商期望收益函数为：

πr(Q)=pEmin{Q,D}+sE(Q-D)+-(cQ-η)(1+r)

(3)

零售商的目标为最大化其期望收益，即：

因为:min{Q,D}=D-(D-Q)+，(Q-D)+=(Q-D)+(D-Q)+，则期望收益函数变为：

πr(Q)=(p-s)μ-(p-s)E(D-Q)+-(cQ-η)(1+r)+sQ

(4)

可知，若求上式的最大值就等价于求下式的最小值：

(p-s)E(D-Q)++(cQ-η)(1+r)-sQ

(5)

因为市场需求D所服从的分布G未知，因此无法运用传统的报童模型处理方法求最优订货量。根据Scarf[21]和Gallego和Moon[22]等对只有期望和方差已知的报童问题的研究文献，对最坏需求分布下的(5)式进行优化。

令ψ为随机变量D的所有可能最坏分布的集合，首先在ψ中找到最坏的需求分布，运用Cauchy-Schwarz不等式，有：

(6)

已经证明，对于任意Q，存在唯一分布G*∈ψ使得(6)式的上界为紧约束，即不等式取等，且G*是最坏的市场需求分布，具体证明，请参看Gallego和Moon[22]、Gallego[23]等文献。然后，在最坏的市场需求分布G*下，(5)式变为：

最后，将目标(5)转变为在最坏的需求分布G*下求最小值，即：

(7)

最终目标(7)的实质是在最坏的情况(最坏的市场需求分布G*)下，求零售商最大的期望收益。

定理3 市场需求的期望和方差已知，零售商的最优订货量Q2满足：

(8)

证明：对M(Q)分别求一阶、二阶导数：

(9)

则M(Q)是关于Q的严格凸函数，存在唯一的Q使得M(Q)最小。设Q2满足(9)式等于零，也即是：

定理得证。

4.2 银行利率决策

两种情形下给出的均是鲁棒的银行收益函数，部分信息可信情形下银行收益函数同样为(2)式。

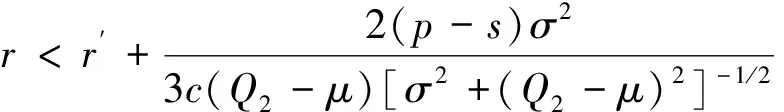
(证明见附录C)

4.3 均衡分析

命题2： 已知均值、方差情景下零售商和银行的Stackelberg博弈存在均衡，且均衡解为Q2*和r2*。其中Q2*、r2*分别满足下面两式：

(证明见附录D)

5 数值分析

通过上述模型分析，得出了相信全部信息与只相信部分信息这两种情况下银行与零售商的Stackelberg博弈均衡解。下面将通过数值的方式对两种情形下的最优订货量决策、最优利率决策、利润以及利润分配进行分析。

5.1 最优订货量与最优利率决策对比分析

假定p=8，c=5，w=4.5，s=3，r′=0.05。已知分布情况下，我们假定市场需求分布服从正态分布。部分信息可信下，已知均值方差，假定μ=100，σ=100,η取[50,550]且为整数中的一部分。分别计算两种情形下零售商最优订货量、银行最优贷款利率、以及零售商贷款量。数值仿真结果如图2所示：

图2 最优利率与最优订货量的关系图

由图2可知，自有资金相同时，两种情形下零售商的最优订货量以及贷款量并没有明显差异。最优贷款利率却有不同的情形：当零售商自有资金充足时，对银行贷款的渴望并不强烈，两种情况下银行最优贷款利率的差异并不明显。随着零售商自有资金的减少，只信部分信息时银行设定的最优贷款利率明显高于相信全部信息时的最优贷款利率。

5.2 均衡利润分析

5.2.1 银行与零售商利润分析

这里分析零售商自有资金相同时，两种情形下零售商和银行的利润情况，数值分析结果如图3、图4所示。

图3 自有资金与零售商利润的关系图

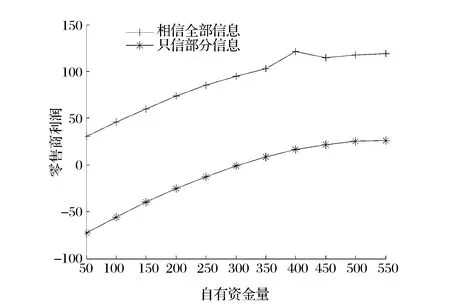
图4 自有资金与银行利润的关系图

由图3可知，自有资金相同，银行相信全部信息情况下，零售商所获利润明显高于银行只信部分信息情况下所获利润，且随着自有资金量的增加，零售商所获利润逐渐提高。由图4可知，自有资金相同，银行相信全部信息的情况下，银行所获利润明显低于只信部分信息的情形。但是，随着零售商自有资金的增加，两种情形下银行所获利润趋于相同且逐渐减少。

5.2.2 整体供应链利润以及利润分配分析

这里将对两种情形下整体供应链利润进行对比，然后分析银行相信部分信息对供应链利润以及利润分配的影响，数值分析结果如图5、图6所示。

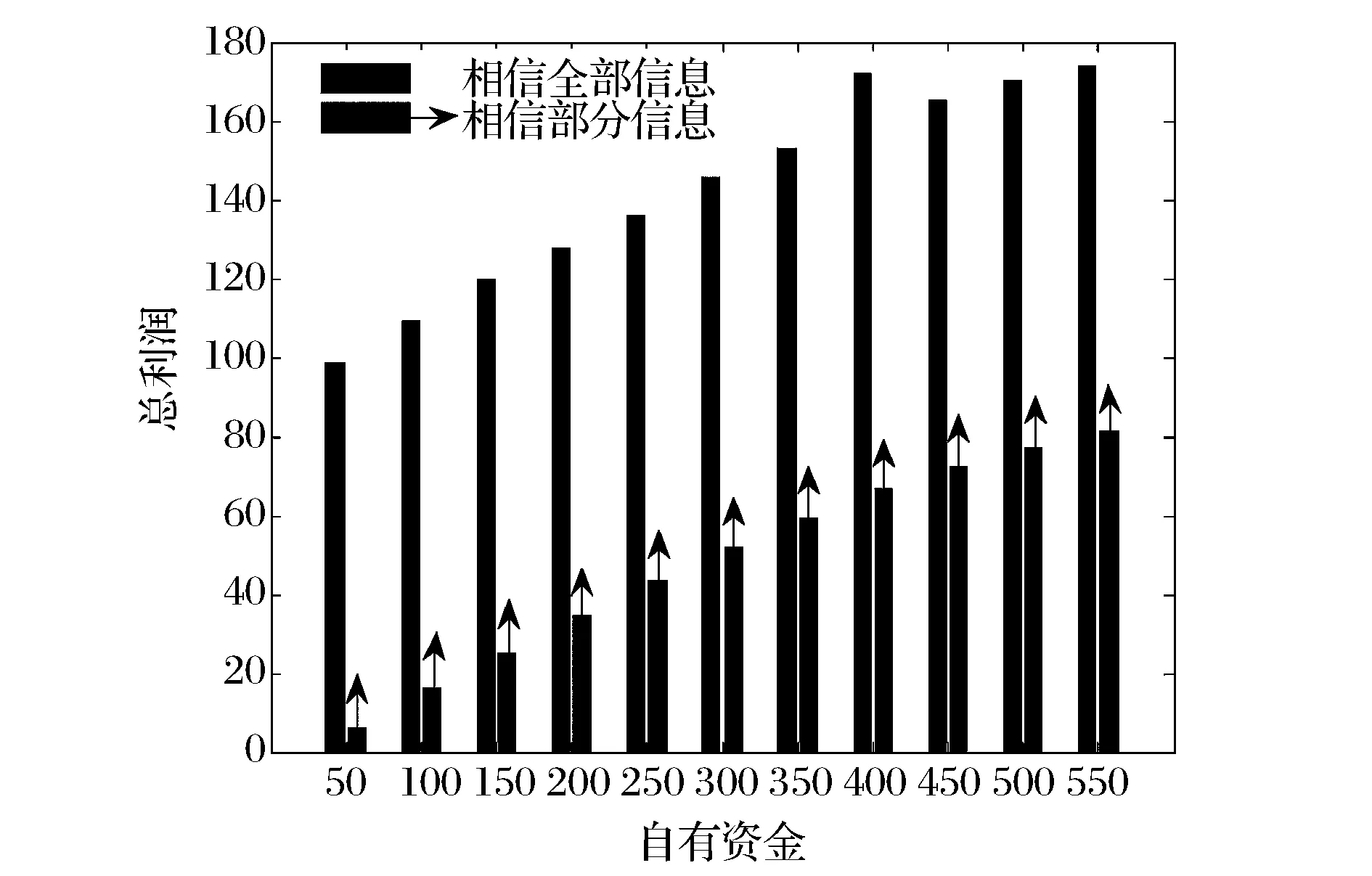
图5 自有资金与零售商利润的关系图

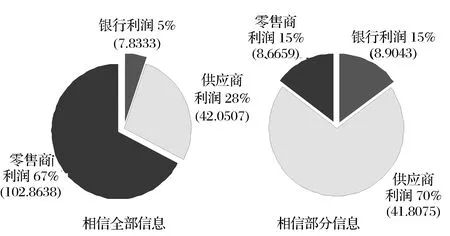
图6 η=350时供应链利润分配对比图

由图5可知，银行只信部分信息的情况下所做的利率决策对供应链整体利润的影响比较大，使供应链整体利润明显下降。由图6可知，银行相信全部信息的情况的决策，能够使得零售商获得整体供应链67%的利润。若银行只信部分信息情况下的决策，使得零售商的利润下降到15%。银行利润由5%上升到15%，但是绝对数额并没有明显改善。可以看出，银行只相信部分信息的利率决策对于供应链整体的运作效率有着非常显著的影响。

6 结语

理论研究和社会事实表明，利率决策对银行和企业的运营极其重要。本文通过分析银行相信全部信息以及只信部分信息下银行和企业的Stackelberg博弈，给出两种情形下博弈的均衡解，并结合数值分析，发现银行可信的信息对于利率决策有着重要的意义，且对于供应链的整体运营效率有着显著的影响。主要结论有：

(1)供应商在两种情况下的绝对收益变化并不明显，而零售商的收益变化巨大，零售商有强烈的意愿使银行相信其提供的全部信息。为了达到此目的，零售商有动力与供应商合作，共同努力获取银行信任，零售商可能会与供应商共享收益。同时零售商也有动力对银行职员进行灰色公关。这在现实生活中有较大的启示性意义((1)式，(3)式和数值分析5.2)。

(2)只信部分信息的情况下，银行设定的最优贷款利率明显高于相信全部信息下的最优贷款利率。只信部分信息下银行的鲁棒决策，使得零售商、供应链的整体利润大幅降低，并且对供应链上利润分配产生较大的影响(定理2，定理4和数值分析5.1)。

(3)自有资金相同时，相信全部信息和只信部分信息两种情形下零售商的最优订货量以及贷款量并没有显著差异，说明了零售商在一定利率范围内对于资金的需求趋向刚性(定理1，定理3和数值分析5.1)。

银行只信部分信息的决策具有较强的保守性，鲁棒决策对供应链利润以及利润分配会产生显著的非积极性的影响。但是金融机构考虑风险性的要求，使得鲁棒决策尤为普遍。对于如何改善鲁棒决策的保守性，本文没有深入研究。另外，银行只信部分信息情况下的决策，对单个企业的影响和参与到供应链合作中对整体供应链的影响的对比，本文也没有深入研究，上述问题有待进一步研究。

附录

A.定理2证明：

对πb(r)分别求r的一阶、二阶导数：

由定理1可知：

B.命题1证明：

结合定理1与定理2得：

考虑下述情景：

(1)当Q=0，F(0)=0，f(0)=0时，

(2)当取Q=∞，F(∞)=1，f(∞)=0时，

Q1*满足：

p-(p-s)F(Q1*)-c[1+r′+

r1*满足：

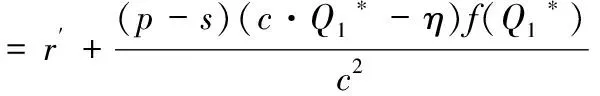
命题得证。

C.定理4证明：

由定理3可知：

+(c·Q2-η)

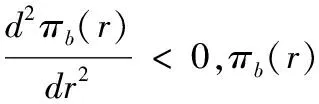
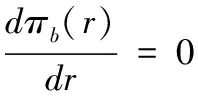
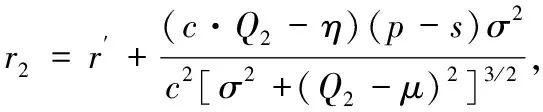
说明：现行政策规定，金融机构放贷利率不能高于国家贷款基准利率的4倍，如果贷款利率过高，致使零售商无利可图，零售商不会选择贷款，所以贷款利率必须会有上界。通过数值的验证，假定符合上述要求。

D.命题2证明：

结合定理4和定理3中(8)式得：

(1)令Q2=0，

命题得证。

参考文献：

[1] 中国新闻网.温家宝江苏考察，称金融机构不能把企业当成唐僧肉[EB/OL].2011-12-20.http://business.sohu.com/20111220/n329675097.shtm-l.

[2] 陈志龙.中小企业融资成本上升，民间借贷链现裂缝[EB/OL].2011-08-16.http://finance.qq.com/a/20110816/000742.htm.

[3] Nahmias S.Production and operations analysis[M].3rd ed.Homewood:Irwin, IL.1997.

[4] Clark A, Scarf H.Optimal policies for a multi-echelon inventory problem[J].Management Science, 1960, 6(4): 475-490.

[5] Deuermeyer B, Schwarz L B.A model for the analysis of system service level in warehouse/retailer distribution systems: The identical retailer case[M].Indiana:Purdue University,1975.

[6] Moinzadeh K, Lee H.Batch size and stochastic levels in multi-echelon repairable systems[J].Management Science, 1986, 32(12): 1567-1581.

[7] Lee H, Moinzadeh K.Operating characteristics of a two echelon inventory system for repairable and consumable items under batch ordering and shipment policy[J].Naval Research Logistics,Quart.1987a, 34(3): 365-380.

[8] Axsäter S, S K Rosling.Installation vs.Echelon stock policies for multi-level inventory control[J].Management Science, 1993, 39(10): 1274-1280.

[9] Modigliani F, Miller M H.The cost of capital, corporation finance and the theory of investment[J].American Economic Review, 1958, 48(3): 261-297.

[10] Brealey R A, Myers S C.Principles of Corporate Finance[J].New York:McGraw-Hill, 1996.

[11] Buzacott J A, Zhang R Q.Inventory management with asset-based financing[J].Management Science, 2004, 50(9): 1274- 1292.

[12] Xu Xiaodong, Birge J R.Operational decisions, capital structure, and managerial compensation: a news vendor perspective[R].Working paper, University of Chicago Graduate School of Business, 2005.

[13] Hu Qiaohai, Sobiel M J.Capital structure and inventory management[R].Working Paper,2005.

[14] Boyabatli O, Toktay L B.Capacity investment in imperfect capital markets: The interaction of operational and financial decision[R].Working Paper, Fontainebleau, France: INSEAD, 2006.

[15] Dada M, Hu Qiaohai.Financing newsvendor inventory [J].Operations Research Letters, 2008, 36(5): 569-573.

[16] Caldentey R, Haugh M B.Supply contracts with financial hedging[J].Operations Research, 2009, 57(1): 47-65.

[17] 陈祥锋，朱道立，应雯珺.资金约束与供应链融资和运营决策研究[J].管理科学学报，2008，11(3)：70-77.

[18] 庞素琳.存在拖欠还款概率影响的信贷风险决策机制[J].系统工程理论与实践，2007，(10) ：31-38.

[19] 钟远光，周永务，李柏勋，等.供应链融资模式下零售商的订货与定价研究[J].管理科学学报，2011，14(6)：57-65.

[20] Cachon G P.Supply chain coordination with contracts[R].Working paper, University of Pennsylvania, Philadelphia, PA.2002.

[21] Scarf H.A min-max solution of an inventory problem[M].California: Stanford University Press, 1958.

[22] Gallego G, Moon I.The distribution free newsboy problem: Review and extensions[J].Operational Research Society, 1993, 44(8): 825-834.

[23] Gallego G.Tight bounds on tail probabilities and other expectations[R].Working Paper, Department of IE & OR, Columbia University,1991.