VaR与CVaR的敏感性凸性及其核估计
黄金波,李仲飞,周先波
(1.广东财经大学金融学院,广东 广州 510320;2.中山大学管理学院,广东 广州 510275;3.中山大学岭南学院,广东 广州 510275)
1 引言
风险价值(Value-at-Risk, 缩写为VaR,)和条件风险价值(Conditional Value-at-Risk, 缩写为CVaR)是当今最为流行的两大风险度量指标。VaR是指给定置信水平和目标时段下预期的最大可能损失[1],这一概念涵盖了不确定性和损失两大风险特征,而且还允许人们根据自己对风险的偏好选择一个特定的主观概率,其对风险的度量方式与人们对风险的心理感受非常接近[2]。所以VaR一经提出,便得到了迅速推广,巴塞尔协议(Basel Accord, 1995)和欧盟资本充足率指导(EU Capital Adequacy Directive, 1996)先后将VaR列入监督指标。在巴塞尔银行监督委员会和国际证券委员会的推动下,VaR逐渐发展为国际上风险度量的通用标准。目前,VaR的应用范围涉及到证券公司、投资银行、商业银行、养老基金及金融监管机构等。
VaR的广泛应用也引发人们对它的深入研究,并开始把VaR与其它指标进行比较。Artzner 等[3]提出一致性风险度量理论,他们认为一致性风险度量工具至少应该满足四个公理性条件:单调性;次可加性;正齐次性;平移不变性。Artzner等[4]指出,VaR不满足一致性风险度量理论中的次可加性公理,也就是说,用VaR度量的组合风险不一定小于单个风险的加总,从而破坏投资组合理论中的风险分散化原理;另一方面,许多学者指出,VaR只报告收益(或损失)分布的一个分位数,并不关心分位数后部的风险分布情况。基于VaR的不足,Rockafellar和Uryasev[5-6]提出CVaR的概念,并证明了CVaR的一致性。CVaR度量的是损失超过VaR水平的条件期望值。CVaR保留了VaR的优点,还弥补了VaR不满足次可加性、没有考虑尾部风险等缺陷,它的计算问题方便处理,是理论界公认的一种比VaR更为合理有效的风险度量工具[7]。然而,刘俊山[8]比较VaR和CVaR的优劣,指出CVaR在性质上要优于VaR,但在椭球分布假定下,VaR依然保持次可加性和二阶随机占优的一致性。由于椭圆分布包含诸如t分布以及帕累托分布等能够反映厚尾特征的分布,因此VaR依然可以刻画金融时间序列数据的尾部特征。同时他指出CVaR在风险管理和监管实践中遇到诸多的问题,例如CVaR模型的事后检验不易实施,所以,VaR和CVaR在度量金融风险上孰优孰劣没有定论。时至今日,VaR和CVaR都被写进巴塞尔协议III作为监管部门的风险度量工具。
VaR和CVaR概念提出之后,如何对它们进行估计成为学者和企业界共同关注的热点问题,其间诞生了一系列的估计方法,Engle和Manganelli[9]将这些估计方法分为三大类:第一类是参数方法,主要包括GARCH族模型和Copula函数法;第二类是半参数方法,主要包括极值理论;第三类是非参数方法。主要包括经验分布函数法和核估计方法。相对于参数半参数方法,非参数方法的优点是不需要事先对分布函数形式做任何的模型设定,避免人为的模型设定风险和参数估计偏差,能够给出较为准确的风险估计。而且非参数核估计方法可以允许金融时间序列数据之间相互依赖[10-11]。
因为上述几方面的优点,近年来非参数核估计方法在VaR和CVaR估计上的应用发展非常迅速。Gourieroux等[12]首次给出了VaR的核估计量但并没有研究该估计量的统计性质。Chen Songxi和Tang Chengyong[11]在较弱的条件下证明了VaR核估计量的一致性和渐进正态性,并且他们发现,与基于经验分布的次序统计量相比,该核估计量具有更小的方差和均方误差。Scaillet[13]首次给出了期望损失(Expected Shortfall, 缩写为ES,在分布函数满足连续性条件下,ES与CVaR相同)的两步核估计公式,并研究了ES的敏感性及其核估计量的大样本性质。Chen Songxi[14]比较了CVaR的非参数核估计量和基于经验分布的次序统计量之间的差别,得出二者在估计的方差和均方误差方面并无明显的差异。国内方面,刘静和杨善朝[7]、赵晓玲等[10]、刘小茂和李楚霖[15]、刘静等[16]以及刘晓倩和周勇[17]从不同角度研究了ES核估计量的统计性质。
虽然金融风险的非参数核估计方法近年来得到较快发展,受到越来越多学者的关注,但学者大多研究VaR和CVaR核估计量的统计性质。少有学者结合投资组合理论来研究VaR和CVaR核估计量的性质,而这对于实践中的风险管理和资产配置至关重要。为此,本文结合核估计方法和投资组合理论研究VaR和CVaR的敏感性和凸性。
2 VaR与CVaR的核估计
2.1 非参数核估计
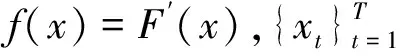
(1)
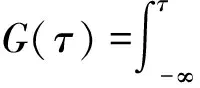
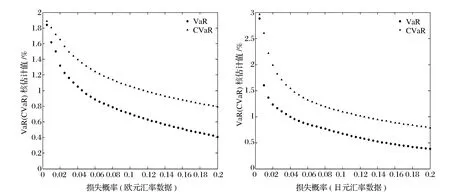
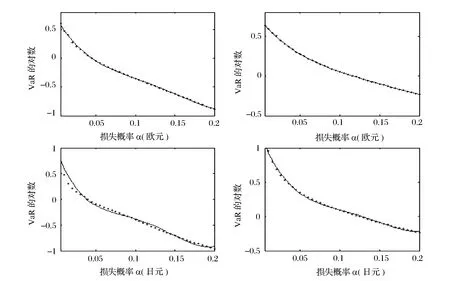
(i)0 (ii)g(-z)=g(z); (2) (3) g1(·),h1为变量Y对应的核函数和窗宽,选取方式同g(·),h。 Y关于X的条件分布的非参数核估计为[18]: (4) 设连续型随机变量ξ是某资产的随机收益率,它的密度函数和分布函数分别为f(·)和F(·),假设F(·)是连续且可导的,记损失概率α下的VaR为v(ξ,α),则根据Jorion[1]的定义,VaR的数学表达式可写为: v(ξ,α):=-inf{z:F(z)≥α}⟹F(-v(ξ,α))=α (5) 记损失概率α下的CVaR为u(ξ,α),根据Rockafellar和Uryasev[5]对CVaR概念的界定,CVaR的数学表达式可写为: (6) (7) (8) (9) 定理1:如果核函数g(·)满足(2)式的条件且α∈(0,1),则方程式(8)有且仅有一个解。 投资组合VaR和CVaR对组合头寸的敏感性和凸性对于风险管理和组合选择至关重要,敏感性是投资组合的风险值对头寸的敏感程度,度量VaR和CVaR随头寸变动的风险,而是否满足凸性关系到能否找到全局最小风险的投资组合问题。本节介绍投资组合VaR和CVaR对头寸的敏感性及其核估计量,下节讨论投资组合VaR与CVaR的凸性。 假设市场上存在n(n>1)种风险资产,第i种资产的收益率为ξi,则ξ=(ξ1,ξ2,…,ξn)′为n种风险资产收益率的随机向量。设w=(w1,w2,…,wn)为投资者所持有的投资组合头寸,则组合的收益率ξw=wξ。记投资组合w在损失概率α下的VaR和CVaR分别为v(w,α)和u(w,α)。则投资组合的VaR数学表达式为: v(w,α):=-inf{z:Fξw(z)≥α}⟹Fξw(-v(w,α))=α 式中,Fξw(·)为ξw的分布函数,假设其连续可导。投资组合的CVaR数学表达式为: 式中,fξw(·)为ξw的密度函数。 (10) (11) 其中,hw为窗宽,可采取前面介绍的拇指法则进行选取。 VaR与CVaR的敏感性被定义为投资组合VaR与CVaR对组合头寸的一阶导数;也有学者称它们为边际VaR(Marginal VaR,记为MVaR)和边际CVaR(Marginal CVaR,记为MCVaR)。用数学符号可表示为: Δwv(w,α)=∂v(w,α)/∂w′;Δwu(w,α)=∂u(w,α)/∂w′ 引理1:投资组合VaR与CVaR对组合头寸的一阶导数分别为[12-13]: Δwv(w,α)=-E[ξ|ξw=-v(w,α)];Δwu(w,α)=E[-ξ|-ξw>v(w,α)] (12) 由于VaR和CVaR都满足正奇次性[4-5],所以对于任意投资组合w,成分VaR之和等于投资组合的VaR;成分CVaR之和等于投资组合的CVaR。即: wΔwv(w,α)=v(w,α);wΔwu(w,α)=u(w,α) 由(12)式可知,MVaR的解析式为条件期望的形式,可利用公式(4)得到其核估计式为: (13) 根据CVaR与MCVaR的关系,MCVaR的核估计量可通过(11)式得到[13]: (14) 在理论上,Artzne等[4]证明VaR不是一致性风险度量,而Rockafellar和Uryasev[5]证明CVaR是一致性风险度量,从而也是凸风险度量。但VaR和CVaR的估计量是否满足凸性并没有学者深入讨论,为此本节进一步讨论投资组合VaR与CVaR的核估计量对组合头寸的凸性,即组合的VaR与CVaR的核估计量是否是组合头寸的凸函数。通常情况下函数凸性与函数的二阶导数矩阵的半正定性是等价的;所以,以下将用投资组合的VaR与CVaR对组合头寸的二阶导数矩阵的性质来讨论凸性问题。 引理2:投资组合VaR对组合头寸的二阶导数矩阵可表示为[12]: (15) 投资组合CVaR对组合头寸的二阶导数矩阵为[15]: (16) 式中p(·)和P(·)分别为-ξw-v(w,α)的密度函数和分布函数,V[·]为方差算子。 由公式(1)可得,投资组合w的密度函数fξw(z)的核估计为: (17) 又因为V[ξ|ξw=z]=E[ξξ′|ξw=z]-E[ξ|ξw=z]E[ξ′|ξw=z] 上式右边是条件期望的形式,所以它们的核估计可通过(4)式得到: (18) p(·)和P(·)分别为-ξw-v(w,α)的密度函数和分布函数,所以根据公式(1)可得: (19) (20) 定理2 投资组合VaR对组合头寸的二阶导数矩阵的核估计式为: (21) 投资组合CVaR对组合头寸的二阶导数矩阵的核估计式为: (22) 证明:当ξ=(ξ1,ξ2,…,ξn)′服从参数为μ和Ω的一般n维椭球分布时,根据Landsman和Valdez[19]的研究,组合收益率ξw的VaR可以表达成:v(w,α)=cα(wΩw′)0.5-wμ,cα>0,简单推导可得: (23) 容易证明上式右边是半正定矩阵。所以多维椭球分布下,v(w,α)是组合头寸的凸函数。 (24) 利用前文的理论分析框架,本节估计我国外汇市场上单项外汇资产和外汇资产组合的汇率风险,并基于外汇组合VaR和CVaR对组合头寸的敏感性和凸性,讨论如何寻找外汇资产的最小风险组合及其对应的最小风险。我们选取欧元和日元汇率的日对数收益率,数据窗口从2011年1月4日至2013年7月6日,共有755个样本,数据来自CCER经济金融数据库,样本数据的描述性统计如表1: 从欧元和日元汇率的标准差来看,欧元汇率的波动更大、风险更大。欧元汇率的偏度系数大于零,说明其分布存在“右偏”;日元汇率的偏度系数小于零,说明其分布存在“左偏”,从而二者分布都不具有对称性;从偏度系数大小来看,日元的非对称性程度更严重。欧元和日元汇率的峰度系数大于3,说明二者的分布比正态分布陡峭,尾部比正态分布厚,存在“尖峰厚尾”现象。JB统计量的值拒绝二者服从正态分布的假设。 把样本数据代入公式(1),核函数选择二阶Gauss核,窗宽采用拇指方法选择,可得到非参数核估计方法下的样本分布,把样本均值和样本方差代入正态分布密度函数公式可得正态分布设定下的样本分布。图1直观地显示,基于非参数核估计方法得到的样本分布比同均值同方差下的正态分布更加陡峭,具有更高的峰和更厚的尾。这也说明正态分布设定会低估尾部风险。 我们把区间(0, 0.2)进行40等分,α取等分点处的值,把样本数据代入(8)和(9)式,取核函数为二阶Gauss核,窗宽依拇指法则选择,这样可以测算不同损失概率下欧元汇率和日元汇率的风险值,结果见图2。由图2可知:(1)随着损失概率的增加,VaR和CVaR的核估计值在减小;(2)CVaR的核估计值大于VaR的核估计值;这两点符合理论预期。(3)随着损失概率的增加,VaR与CVaR减小的速度在下降,即图2中点所形成的曲线变得更加平缓。另外,图2中的曲线与指数函数图像十分相似,这促使我们设想利用一个指数函数来拟合图2中的点。利用图2中的样本点,对VaR和CVaR核估计值取自然对数,利用线性回归得到如下结果: 表1 欧元和日元汇率日对数收益率的描述性统计 图1 欧元和日元汇率日对数收益率的样本分布 图2 欧元和日元汇率的风险测算(核估计方法) (25) (26) (27) (28) 接下来,考虑欧元和日元外汇资产组合的风险估计,并寻找二者的最小风险组合及其对应的最小风险。假设投资者的财富被标准化为1,只在欧元和日元之间进行投资。将区间(0,1)分成100等分,把等分点作为欧元头寸,日元头寸就等于1减去欧元头寸,这样就构成了欧元与日元的100个投资组合,取α=5%,利用公式(10)和(13)可以估计每个投资组合的VaR和MVaR,利用公式(11)和(14)可以估计每个投资组合的CVaR和MCVaR,计算结果见表2。 从表2的结果来看,随着欧元头寸的增加,组合的风险值(VaR或CVaR)先下降后上升,所以存在最小风险组合。若用VaR来度量风险,则欧元和日元的最小风险组合为(0.47, 0.53);若用CVaR来度量风险,则欧元和日元的最小风险组合为(0.51, 0.49)。在最小VaR组合处,欧元和日元MVaR近似相等,同样在最小CVaR组合处,欧元和日元的MCVaR近似相等(见图4)。从图4中还可以看到,组合VaR (CVaR)对欧元头寸的导数随欧元头寸的增加而上升,即欧元头寸越大,组合的风险对其越敏感。相反组合VaR (CVaR)对日元头寸的导数随欧元头寸的增加而呈下降趋势。 图3 VaR (CVaR)核估计值与损失概率关系拟合 表2 组合的VaR (MVaR)和CVaR (MCVaR)估计结果(α=5%) 图4 欧元与日元组合的VaR (CVaR)核估计值图 图5 组合VaR (左)与CVaR (右)的凸性 为了检验欧元和日元组合的风险是否具有凸性,即组合的VaR和CVaR是否是组合头寸的凸函数,我们把区间(-1, 1)进行40等分,把等分点作为欧元头寸和日元头寸的取值,这样就构成了1600个组合,利用公式(10)和(11),可以估计每个组合处的VaR和CVaR,限于篇幅计算结果不再列出,仅把结果绘成图5,从图形上来看,欧元和日元组合的VaR和CVaR是组合头寸的凸函数,这一性质就意味着我们可以在凸可行集约束下找到全局最小风险组合及其对应的最小风险,这为进一步的风险优化和组合选择问题提供了方便。 本文给出VaR与CVaR的核估计量,讨论了投资组合VaR与CVaR对组合头寸的敏感性和凸性,并利用核估计方法对投资组合VaR与CVaR一阶导数向量和二阶导数矩阵进行估计。中国外汇市场数据的实证结果显示:核估计方法能够抓住我国外汇市场汇率波动存在的“尖峰厚尾”、“左偏”等特征,并能得出外汇组合的敏感性和凸性特征。本文的研究对于风险管理和投资组合选择具有重要意义,下步研究可把本文得到的组合VaR与CVaR的核估计量、一阶导数向量和二阶导数矩阵的核估计量嵌入风险最小化模型和均值-风险优化模型,实现风险估计与风险管理、组合选择问题同步进行。避免事前的分布假设,减小或消除模型设定风险。 参考文献: [1] Jorion P.Value at Risk[M].2nd New York:McGraw-Hill, 2001. [2] 姚京,袁子甲,李仲飞.基于相对 VaR 的资产配置和资本资产定价模型[J].数量经济技术经济研究, 2005, 12:133-142. [3] Artzner P, Delbaen F, Eber J M, et al.Thinking coherently[J].Risk, 1997, 10: 68-71. [4] Artzner P, Delbaen F, Eber J M, et al.Coherent measures of risk[J].Mathematical Finance, 1999, 9(3):203-228. [5] Rockafellar R T, Uryasev S.Optimization of conditional value-at-risk[J].The Journal of Risk, 2000, 2(3):21-41. [6] Rockafellar R T, Uryasev S.Conditional value-at-risk for general loss distributions[J].Journal of Banking and Finance, 2002, 26(7): 1443-1471. [7] 刘静,杨善朝.风险度量ES的非参数估计[J].工程数学学报,2009,26(4):577-585. [8] 刘俊山.基于风险测度理论的VaR与CVaR的比较研究[J].数量经济技术经济研究, 2007,3:125-133. [9] Engle R F, Manganelli S.CAViaR: Conditional autoregressive value at risk by regression quantiles[J].Journal of Business & Economics Statistics, 2004,(22): 367-381. [10] 赵晓玲,陈雪蓉,周勇.金融风暴中基于非参估计VaR和ES方法的风险度量[J].数理统计与管理, 2012,31(3):381-383. [11] Chen Songxi, Tang Chengyong.Nonparametric inference of value-at risk for dependent financial returns[J].Journal of Financial Econometrics, 2005, 3(2):227-255. [12] Gourieroux C, Laurent J P, Scaillet O.Sensitivity analysis of values at risk[J].Journal of Empirical Finance, 2000,7(3):225-245. [13] Scaillet O.Nonparametric estimation and sensitivity analysis of expected shortfall[J].Mathematical Finance, 2004, 14(1):115-129. [14] Chen Songxi.Nonparametric estimation of expected shortfall[J].Journal of Financial Econometrics, 2008, 6(1):87-107. [15] 刘小茂, 李楚霖.资产组合的CVaR风险的敏感度分析 [J].数学物理学报, 2004, 24A(4): 442-448. [16] 刘静,杨善朝,姚永源.α-混合序列下期望损失ES的两步核估计[J].应用概率统计,2010,26(5):485-500. [17] 刘晓倩,周勇.金融风险管理中ES度量的非参数方法的比较及其应用[J].系统工程理论与实践, 2011,31(4):631-642. [18] Li Qi, Racine J S.Nonparametric Econometrics: Theory and Practice[M].New Jersy:Princeton University Press, 2007. [19] Landsman Z M, Valdez E A.Tail conditional expectations for elliptical distributions[J].North American Actuarial Journal, 2003, 7(4): 55-71.



2.2 VaR与CVaR的核估计
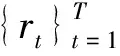
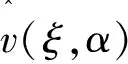



3 VaR与CVaR对头寸的敏感性
3.1 投资组合的VaR与CVaR

3.2 VaR与CVaR的敏感性
4 VaR与CVaR的凸性



5 实证分析





6 结语

