一种运动学控制律的无人地面车辆轨迹跟踪方法

王 恒， 胡军中， 闫永宝， 张舒阳

(1. 装甲兵工程学院控制工程系，北京100072； 2. 浙江美科斯叉车有限公司，浙江 杭州 311407)

由于无人地面车辆(Unmanned Ground Vehicle，UGV)具备遥控和自主驾驶能力，并能对信息进行采集和处理，因而在炸药引爆、场地勘探、安全巡逻、战场营救等领域发挥着重要作用，而且随着技术研究的深入，其应用范围得到不断拓展[1-3]。

轨迹跟踪是UGV运动控制问题的研究重点，也是实现许多其他功能的前提。在给定参考轨迹的情况下，通过对车辆位姿信息的采集和处理，经控制算法运算，将得出的控制量赋予车辆执行机构，能够实现对给定轨迹的跟踪。而轨迹跟踪的关键是控制算法的制定，基于不同的思想，为改进控制算法，提高跟踪效果，许多学者进行了深入研究[4-8]。在运动学控制算法中，如何调整车的行驶方向是一个重要的问题，其直接影响到跟踪误差收敛的速度。文献[9]给出了一种始终保持车体朝向参考点位置坐标的算法，虽简单易行，但跟踪效果不是总能达到要求[10]。也有学者提出使用2个模糊控制器分别控制线速度与角速度，进而得到调整车体朝向角的策略[11]，虽有一定效果，但控制规则的制定需大量经验基础，实现和优化起来比较困难。

为此，笔者基于优化车体方向角调整策略的思想，提出了一种运动学控制算法，并与文献[12]给出的基于反步法的控制律进行了仿真跟踪对比，证明了该算法的有效性。

1 运动学模型及跟踪控制问题描述

为便于分析，运动学建模过程中假定UGV同侧车轮转速保持一致，车体为刚性框架，车轮为刚性轮，重心与几何中心重合，且与地面间为纯滚动，忽略滑转与滑移。跟踪位姿状态如图1所示，在全局坐标系XOY中，UGV当前位姿坐标为(Xc,Yc,θc),参考点位姿坐标为(Xr,Yr,θr)；在局部坐标系xoy中，当前位姿和参考点位姿坐标分别为(xc,yc,θc)和(xr,yr,θr)。

图1 跟踪位姿状态

令(Xe,Ye,θe)和(xe,ye,θe)分别为全局坐标系和局部坐标系下的位姿误差,由图1可得

令车体的线速度为v，角速度为w，则速度与位姿坐标之间存在如下关系[13]：

进而得到

(1)

2 控制律设计及稳定性分析

2.1 跟踪控制律设计

定义辅助变量如下：

(2)

(3)

式中:L为当前位置与参考点之间的距离；φ为L与车体当前朝向到参考点转过的角度。极坐标系下的误差可用L、φ和θe表示，即

(4)

结合式(1)、(4)，可以得到[12]

(5)

在轨迹跟踪问题中，首要考虑的是当前点与参考点之间的距离，即L的大小。为使L趋近于0，可将UGV的线速度视作2个方向速度的合成，即

ν=f(νl,νr)，

式中：|νl|=KνL，νl的方向是从当前点指向参考点，起到逐步减小L的作用，Kν为一个恒大于0的参数；νr为参考点的线速度，作用是确保跟踪上参考轨迹。如图1所示，定义辅助变量ν′,其大小及与X轴方向的夹角分别为

(6)

(7)

控制量ν的大小取为νl和νr在车体纵向速度方向上的投影之和，即

ν=νlcosφ+νrcosθe，

(8)

将|νl|=KνL代入式(8)，得到线速度的控制律为

ν=KνLcosφ+νrcosθe。

(9)

由图1可见：要使车辆沿ν′方向行驶，须通过给定合适的控制量ω来调整车体方向角与θ′重合。给出角速度的控制律如下：

(10)

式中：Kω为一个恒大于0的参数。

由式(7)可得

(11)

(12)

式中：

(13)

(14)

由vl=KvL和式(5)可得

(15)

综合式(10)-(15)，得到角速度的控制律如下：

ω= [β2+v′(Kω(vlsinφ+vrsinθe)+

Lsinφ)]/(1-β1)。

(16)

2.2 稳定性分析

为证明式(9)、(16)所给出控制律的稳定性，定义李雅普诺夫函数如下：

V=L2/2+1-cos(θ′-θc)。

(17)

由式(17)可见：V≥0，当且仅当qe=0时，V=0。对V求导，可得

(yeω-ν+νrcosθe)xe+(-xeω+νrsinθe)ye+

Lcosφ(νrcosθe-ν)+Lνrsinφsinθe+

[((β1-1)ω+β2)(vrsinθe+vlsinφ)]/v′。

(18)

将νl、ν和ω的表达式代入式(18)，可得

Lvrsinφsinθe+Kω(vlsinφ+vrsinθe)+

Lsinφ(KvLsinφ+vrsinθe)=KνL2-

Kω(KνLsinφ+vrsinθe)2，

(19)

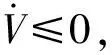
3 算法仿真

笔者运用Matlab/Simulink对本文提出的算法和Kanayama算法[12]进行了圆形轨迹仿真跟踪对比，以验证本文算法的跟踪效果。

参考曲线参数为：νr=1 m/s,ωr=0.1 rad/s，(Xr(0),Yr(0),θr(0))=(30,0,π/2)； UGV初始点位姿为(25,0,0)；试验中控制参数取为Kv=0.8，Kω=2。跟踪仿真效果如图2-8所示。

从仿真结果可以看出：本文提出的跟踪算法能有效跟踪圆形轨迹，与Kanayama算法相比，误差收敛速度更快，且所需速度与角速度分配也更加合理。

图2 跟踪圆形轨迹结果

图3 距离误差变化曲线

图4 X方向误差变化曲线

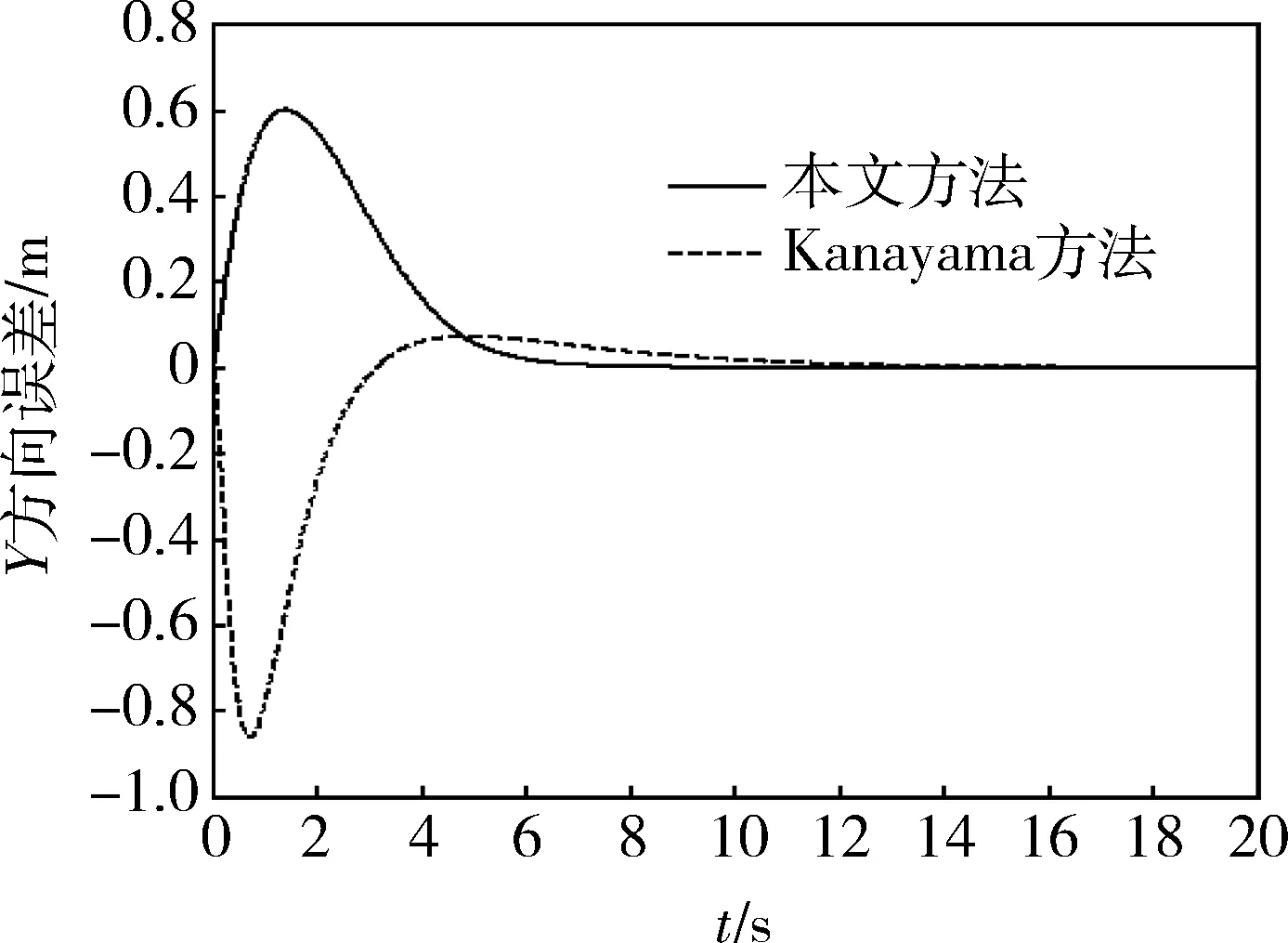
图5 Y方向误差变化曲线

图6 方向角误差变化曲线

图7 角速度变化曲线

图8 线速度变化曲线

4 结论

针对UGV轨迹跟踪问题,本文提出了一种基于极坐标运动学的控制算法。该算法的核心思想是通过对车体方向角调整算法的优化，使UGV时刻沿着更为合适的方向前进，进而达到提高跟踪效果之目的。由于控制算法中只需调节2个参数，因而与模糊控制等需要大量经验基础的算法相比，实现和优化的过程更加简单。从仿真结果来看：该算法能够有效实现UGV的轨迹跟踪，误差收敛速度较快。

参考文献：

[1] 岳松堂，张志杰.外军无人地面车辆发展分析[J].现代军事，2007(11)：53-56.

[2] 刘向平，薛杰.无人地面车辆：地面战争的新利器[J].国外坦克，2013(3)：45-52.

[3] 满益明，陈慧岩，胡玉文，等.无人地面平台研究概况及其关键技术[C]∥中国汽车工程学会越野车技术分会.2008年学术年会论文集.北京：北京理工大学出版社，2008：55-64.

[4] Moon H C, Lee J C，Kim J A, et al. Development of Unmanned Ground Vehicles Available of Urban Drive[C]∥Proceedings of International Conference on Advanced Intelligent Mechatronics. Singapore: Institute of Electrical and Electronics Engineers Inc,2009: 14-17.

[5] Woo H J, Yoon B J, Cho B G, et al. Research into Navigation Algorithm for Unmanned Ground Vehicle Using Real Time Kinematic (RTK)-GPS [C]∥Proceedings of ICROS-SICE International Joint Conference. Japan:Society of Instrument and Control Engineers, 2009:18-21.

[6] Filipescu A, Minzu V, Dumitrascu B, et al. Trajectory-tracking and Discret-time Sliding-mode Control of Wheeled Mobile Robots [C]∥Proceedings of IEEE International Conference on Information and Automation. Piscataway, USA: IEEE Computer Society Press,2011:27-32.

[7] Kao Y F, Chien Y H, Li I H, et al. Design and Implementation of Adaptive Dynamic Controllers for Wheeled Mobile Robots[C]∥Proceedings of ICSSE 2013 IEEE International Conference on System Science and Engineering. Oxford,United Kingdom: Elsevier Ltd, 2013: 195-199.

[8] Al-Araji A S, Abbod M F,Al-Raweshidy H S,et al. Design of an Adaptive Nonlinear PID Controller for Nonholonomic Mobile Robot Based on Posture Identifier[C]∥Proceedings of IEEE International Conference on Control System, Computing and Engineering. Piscataway, USA: IEEE Computer Society Press,2011: 337-342.

[9] Chwa D. Tracking Control of Differential-drive Wheeled Mobile Robots Using a Backstepping-like Feedback Linearization[J].IEEE Transactions on Systems, Man, and Cybernetics,2010,40(6): 1285-1295.

[10] Amoozgar M H, Zhang Y M. Trajectory Tracking of Wheeled Mobile Robots: A Kinematical Approach[C]∥Proceedings of 2012 8th IEEE/ASME International Conference on Mechatronic and Embedded Systems and Applications.Washington,DC,USA: IEEE Computer Society Press,2012: 275-280.

[11] Amoozgar M H, Sadati S H, Alipour K. Trajectory Tracking of Wheeled Mobile Robots Using a Kinematical Fuzzy Controller[J].International Journal of Robotics and Automation,2012, 27(1): 49-56.

[12] Kanayama Y, Kimura Y, Miyazaki F. A Stable Tracking Control Method for Autonomous Mobile Robot [C]∥Proceedings of 1990 IEEE International Conference on Robotics and Automation. Cincinnati, USA:IEEE Computer Society Press,1990: 384-389.

[13] 徐俊艳, 张培仁. 非完整轮式移动机器人轨迹跟踪控制研究[J].中国科学技术大学学报，2004，34(3)：376-380.