基于环境感知的无人车避障系统建模与仿真

毕书浩，李守成

(南京理工大学 机械工程学院，江苏 南京 210094)

0 引言

随着汽车行业的不断发展，汽车在人类生活中越来越普及，随之而来的是交通事故的频繁发生。汽车追尾碰撞是交通事故的主要原因，因此行驶车辆之间保持可靠的安全距离极其重要。无人车以车载计算机为核心，利用车载传感器来感知周围环境，获取道路前方区域内信息，自动控制车辆的速度和方向，使其能够在道路上安全行驶。不仅可以大大减少交通事故，提高汽车主动安全性，同时也减轻驾驶员负担，提高了乘坐舒适性［1］。

现有的无人车避障系统中存在很多问题，一方面大都采用固定安全车距或根据经验公式的安全距离计算模型，这大大降低了道路的通行能力和车辆的行驶安全性;另一方面当系统判定平台需要减速时，没有考虑两车间的距离和相对速度就采取完全制动，则会对平台行驶平稳性产生影响。针对现有避障系统的不足，系统采用了动态安全距离模型，基于模糊控制与最优控制理论设计了避障控制器，对典型工况进行了仿真验证。

1 安全距离模型的建立

动态安全距离数学模型以前车B的运行状态作为参考，把前车B分为静止、匀速或加速运动、减速或减速停止等三种状态［2］，安全距离计算公式一般为:

式中SA为自车A制动距离;SB为前车B制动距离。文中自车A指无人平台，前车B指无人平台前方同一车道内的运动车辆。ΔS的选取对系统安全性及虚警率有一定的影响，为保证充分的安全距离，在本文中取ΔS=5m［3］。根据《汽车理论》制动距离分析过程［4］及式(1)，可推导出动态安全距离数学模型为:

式中υa0为自车A制动前的初速度，单位为m/s;υb0为前车B制动前的初速度，单位为m/s;τ1为制动器传递延迟时间，单位为s。

2 模糊最优控制器设计

2.1 LQR最优控制

自车A在行驶过程中控制器一直起作用，要在尽可能小的加速度波动情况下跟踪前车B行驶，需要设计合适的状态反馈控制规律控制加速度的输出u(t)［5］。定义控制误差为安全距离D与相对距离的差值，即:

根据二次型性能泛函的一般形式采用的指标函数表达式为:

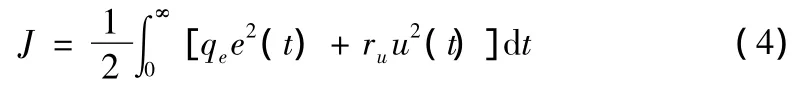
式中qe、ru分别为控制误差和控制量的加权值。

为使J取最小值，根据最优跟踪问题的求解方法，可转化为:

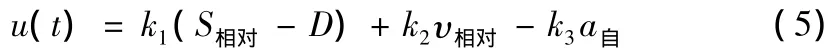
2.2 模糊变量的选取及规则库的建立

最优控制理论基于推导的数学模型，建立的数学模型忽略了模型未知因素，因此在最优控制理论的基础上结合模糊控制理论，可使系统达到较好的控制性能。本文设计的模糊控制器是一个双输入、单输出的模型［6］，以相对距离与安全距离的差值Ds和相对速度Vr作为输入变量，以自车A的加速度a作为输出变量［7］。相对车速的模糊论域范围取［－0.8，0.8］，实际车距与相对距离差值的模糊论域取［－2，4］，输出加速度模糊论域取［－8，8］。

根据驾驶员的实际驾驶经验，并通过反复试验调试，建立的避障模糊规则如表1所示。

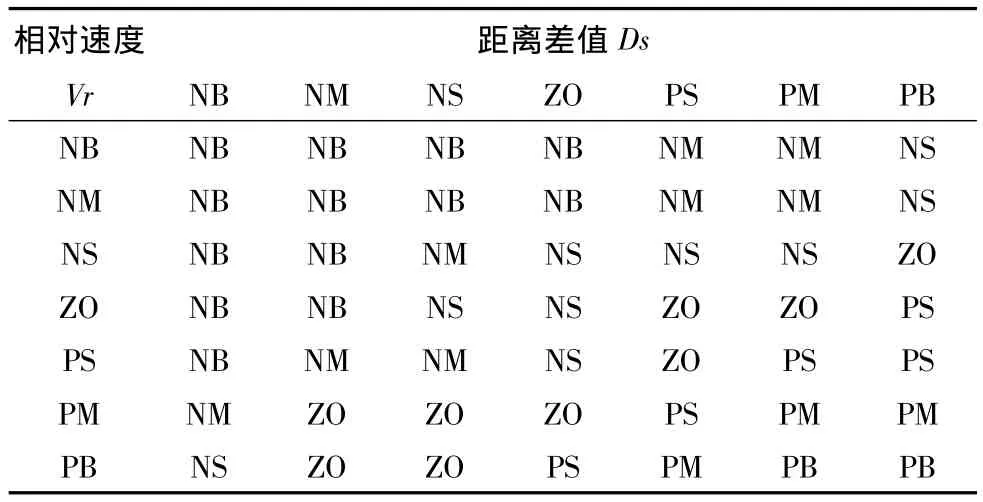
表1 避障系统模糊控制规则

3 安全距离模型仿真及结果分析

根据推导出的动态安全距离模型，在MATLAB/Simulink仿真环境下建立模糊最优避障系统仿真模型，并对前车B不同的运行状态下进行仿真研究，以验证所提算法的准确性。

(1)假设前车B静止，自车A以较低车速12m/s行驶，在某一时刻两车相距30m。自车A完全停止时停止仿真，其仿真运动过程如图1所示。

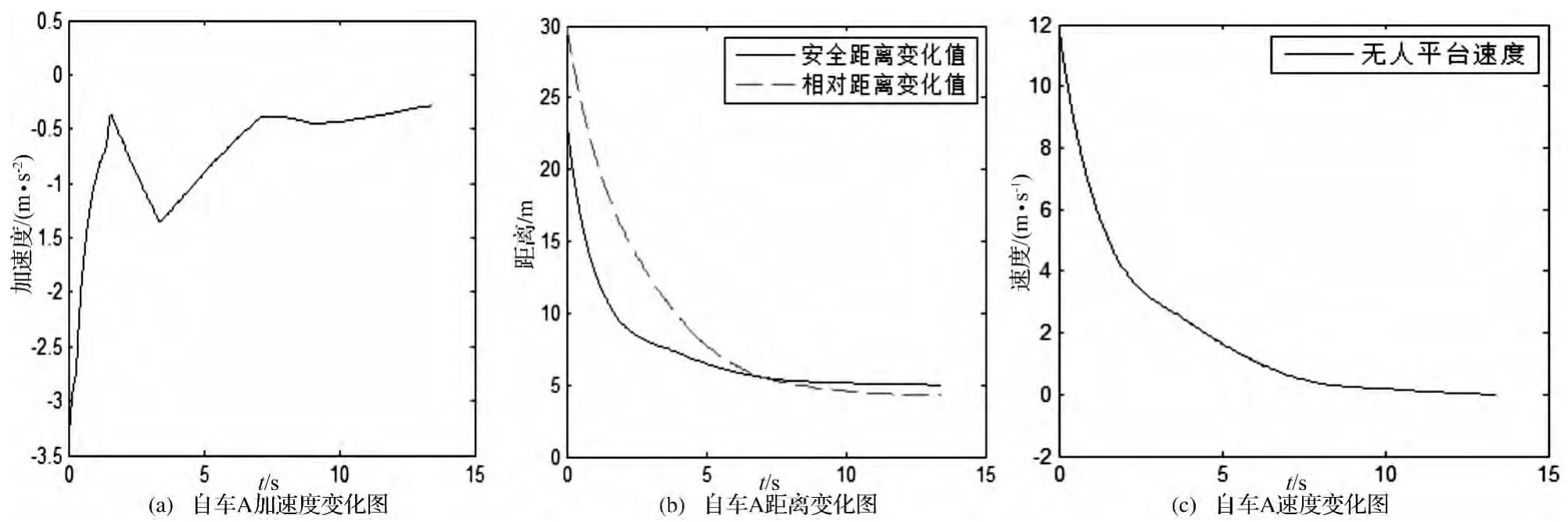
图1 工况(1)仿真结果

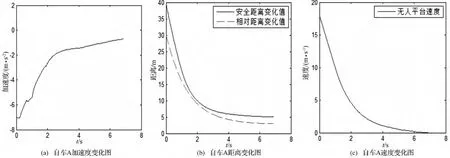
图2 工况(2)仿真结果

从图1可以看出，在初始时刻，两车相对距离略大于自车A行驶的安全距离，自车A采取了适度的制动措施，随着相对距离与安全距离差值的渐渐增大，自车A制动减速度逐渐减小，直至自车A完全停止，此时距离前车B5m左右。

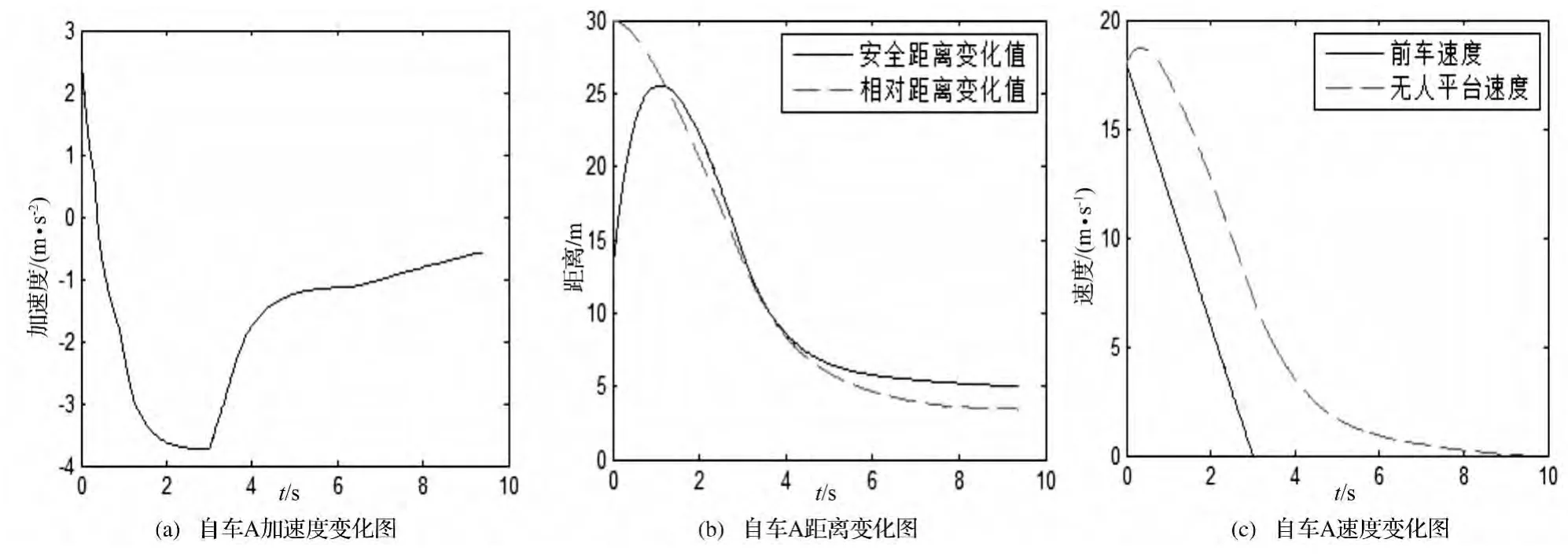
图3 工况(3)仿真结果

(2)假设前车B静止，自车A以较高车速18m/s行驶，在某一时刻两车相距30m。自车A完全停止停止仿真，其仿真运动过程如图2所示。

从图2可知，在初始阶段，自车A速度较大时，安全距离大于相对距离，自车A采取了较大的制动措施，随着速度的降低，相对距离与安全距离的差值也越来越小，自车A的制动减速度逐渐减小，直至停止行驶，此时距离前车B2m左右。

(3)假设前车A突然以6m/s2的减速度紧急制动时，两车行驶初速度均为18m/s，两车相距30m，仿真时间10 s，在自车A完全停止时停止仿真，其仿真运动过程如图3所示。

从图3可知，在初始阶段，相对距离大于安全距离，自车A采取了相应的加速运动，安全距离随之增大。随着两车相对距离的减少，制动减速度逐渐增大;在3 s前车停止时刻，相对速度达到最大值，自车A继续减速直至制动停止，此时距离前车B4 m左右。

4 结束语

本文建立的动态安全距离模型能动态反应车辆行驶的一般驾驶规律，并把最优控制技术运用到模糊控制理论中，保证了车辆道路行驶的通过能力和主动安全性，得出以下结论:

(1)动态安全距离模型考虑了前后两车的行驶状态，前车B处于不同的状态时，安全距离模型不同。

(2)结合模糊控制理论技术，提出的控制策略符合驾驶员驾驶一般规律，两车相对距离较大时，自车A进行了加速运动;相对距离较小时，采取了制动减速措施。

(3)本文在环境感知技术基础上搭建的最优模糊控制系统仿真环境对典型工况下的安全距离模型进行了仿真分析，结果表明在两车完全停止时，两车相对距离仍在2m～5m范围内，安全距离模型较准确，系统可靠性好。

［1］ 吴翠娟，章磊，费树岷.基于图像处理的高速公路汽车防追尾系统研究［J］.电气自动化，2011，33(6):61.

［2］ 许颖.基于模糊理论的车辆防碰撞预警系统研究［D］.湖南:湖南农业大学，2010.

［3］ 旷彪.汽车追尾防碰撞控制系统的研究与仿真［D］.湖南:长沙理工大学，2011.

［4］ 余志生.汽车理论［M］.北京:北京机械工业出版社，2006:97－100.

［5］ 李朋，魏民祥，侯晓利.自适应巡航控制系统的建模与联合仿真［J］.汽车工程，2012，34(7):624 －625.

［6］ 石辛民，郝整清.模糊控制及其MATLAB仿真［M］.北京:清华大学出版社;北京交通大学出版社，2008.

［7］ 王熔熔，李朋.基于模糊控制的汽车避障系统建模与研究［J］.公路与汽车，2012，28(2):12－13.