车轮踏面外形测量的数值处理
(同济大学铁道与城市轨道交通研究院,201804,上海∥第一作者,硕士研究生)
车轮踏面外形测量的数值处理
陈国锋 王 捷 钟晓波 沈 钢
(同济大学铁道与城市轨道交通研究院,201804,上海∥第一作者,硕士研究生)
针对轨道交通车轮踏面外形设计的需要,在给定的误差范围内,提出了将离散数据拟合成圆弧与直线的算法,并研制了相应的计算机程序。通过实例验证了该拟合方法的简便性、可行性与实用性。拟合后的圆弧直线能方便工程应用,适用于数控机床的数据输入和规范化管理。
踏面;外形测量;数值处理
First-author's address Urban Mass Transit Railway Research Institute,Tongji University,201804,Shanghai,China
踏面外形的离散化设计已成为一种趋势[1]。这样可以最大限度地获得最优化的外形,也与现有的算法兼容。但轮轨外形的表达通常要求是圆曲线和直线段的组合,并且圆曲线在交点处一阶导数连续。这种要求的合理性不仅出于传统的习惯,也与不落轮数控机床的应用有关。对于成百上千的离散数据,如在加工过程中将一个个数据输入到机床中,不仅效率低、不易检查错误,而且极易导致输入错误数据。若能符合传统的习惯,又能在给定的精度范围内拟合出与离散点曲线接近的圆弧和直线组合曲线,则可以使新的设计方法工程化。
将离散数据拟合成曲线是数值计算中的通常问题,已有很多算法[2-9],如基于最小二乘法数据拟合、小波函数的数据拟合、多项式数据拟合和整体最优双圆弧最优方法拟合等。用最小二乘法和多项式拟合而成的高次分段函数虽然能保证较高精度,但由于得出曲线较复杂,与实际要求不符。应用小波函数的数据拟合同样有拟合得到函数较复杂的问题,也不适合于工程应用。最优双圆弧最优法拟合的目标也是将离散数据拟合成圆弧,虽然精度较高,但该方法较复杂,拟合段数很多,应用效果不好。针对轨道交通轮轨型面曲线的特殊要求,目前仍没有合适的算法,本文提出一种简单的将离散数据拟合成直线或圆弧的新算法,能保证精度,且拟合段数少。
1 数据拟合计算方法
数据拟合的重点,在于如何获得明确的曲线拟合数据,且能保证拟合精度。本文提出的数据拟合计算方法步骤如下:
(1)确定第一次拟合的切线斜率。可通过最小二乘法获得,其公式为:
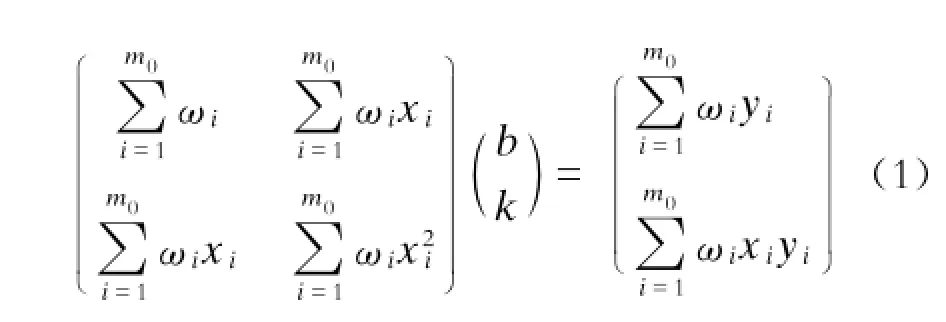
式中:
(xi,yi)---待拟合的离散数据的坐标;
m0---确定切线的离散数据的点数,m0不宜取太多和太少,可根据离散数据的间隔大小来选取;
ωi---点xi处的权,一般取1。
(2)确定第一次拟合初始点。将离散数据第一点投影到由步骤(1)得到的切线上,根据式(2)、(3)得到第一次拟合初始点(x0,y0)。
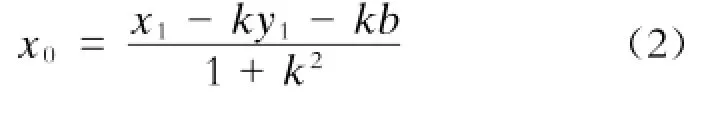

(3)确定圆心所在位置。如图1所示,取一定点数(m)的离散数据进行拟合,由第一点与最后一点确定直线:
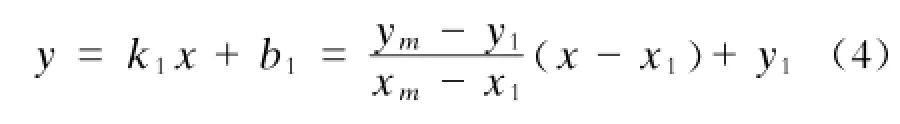
求这m点数据到该直线的距离和:

根据以下原则判断圆心的位置:
S>0且k1>0或S<0且k1<0,圆心在直线靠近x轴的正无穷大方向的那一侧;
S<0且k1>0或S>0且k1<0,圆心在直线靠近x轴的负无穷大方向的那一侧。
(4)进行半径搜索,取初始值。该值为步骤(3)已选择进行拟合离散数据的最后一点到圆心所在直线的距离。

圆心(xc,yc)可由r0、圆心所在的直线和圆心方位确定。
求各离散数据与拟合圆弧的法向误差和:
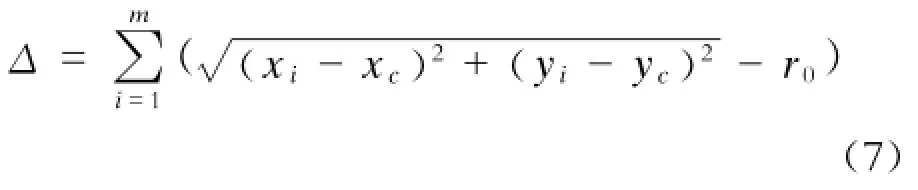
增大半径r1=r0+Δr(Δr为搜索步长,初始值可取一个较大的数),重新计算新半径下的法向误差和Δ′,若Δ′与Δ异号,则半径变为r2=r1-Δr/2;若同号,则半径继续增加,变为r2=r1+Δr。按该方法不断进行搜索,直到法向误差和的异号次数达到n次或法向误差和为0,则终止循环,得到该点数下拟合的最优半径r。
(5)根据步骤(4)得到的半径r,计算此时的法向误差的标准差。若该值小于或等于由外部输入的标准差值,则增加离散数据的点数,m′=m+p,按步骤(4)重新搜索最优半径;反之,则减少离散数据的点数,m′=m-p,重新搜索最优半径。不断进行该循环,p步长由大逐渐减少到1进行计算,直到找到符合输入标准差值的最佳离散点数。
(6)确定用圆弧或直线拟合。判断圆弧半径r是否大于2 000 mm(也可选其他较大值),若r大于2 000 mm,则选择用直线拟合。直线拟合思路与圆弧类似,这里不再赘述。
(7)为保证下段待拟合离散数据能拟合成功,应控制拟合后曲线的切线与待拟合数据的夹角大小。可根据夹角公式获得。
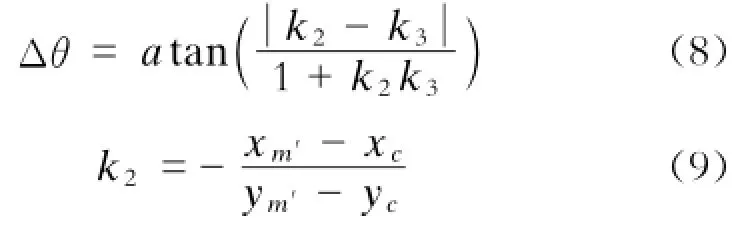
m′为由步骤(5)得到的最佳离散点数。k3的计算方法与步骤(1)中的k相同。若Δθ大于角度差,则减少拟合的离散点数m′重新计算k2、k3和Δθ,直到满足角度差要求。第一次拟合结束。
(8)进行第二次拟合。第二次拟合应保证与前一段曲线相切(如图2),故应保证第二次拟合初始点与前一段最后一点相同(A点)及切线斜率相等。此后的计算方法同步骤(3)~(7),不再赘述。
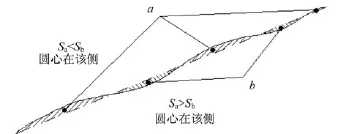
图1 圆心位置判断示意图

图2 相邻曲线相切
2 计算方法的程序编制
基于以上算法,用Matlab编制了拟合离散数据程序。其中,当拟合圆弧半径大于2 000 mm时,改用直线拟合,拟合结束后生成一个result.txt曲线信息和normal_err.txt法向误差文件,以便进行下一步。程序流程如图3所示。程序拟合界面和拟合图形如图4所示。
3 拟合实例
3.1 任意曲线的拟合
为验证算法的通用性,对图5所示的正弦离散数据曲线进行拟合计算分析。正弦函数含有10 001个离散点,设定控制标准偏差在0.01 mm,角度偏差为0.04 rad。拟合结果见图5(截取原始数据第一个周期),拟合后的段数为128段。
将含有401个离散数据的2段相切圆弧导入该软件,设定控制标准偏差为0.01 mm,角度差为0.04 rad。拟合情况如图6所示,拟合后段数只有4段。
3.2 踏面外形的拟合
将含有2 094个离散点的踏面外形x,y坐标导入该软件,设定控制标准偏差为0.1 mm,角度偏差为0.04 rad。踏面拟合情况见图7,拟合后的段数只有12段。
4 拟合结果分析
将轮轨踏面的拟合结果与拟合之前的数据进行轮径差曲线与接触关系对比,如图8与图9所示。
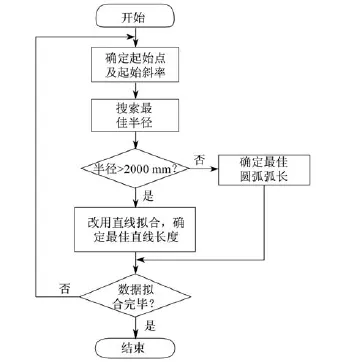
图3 程序流程图
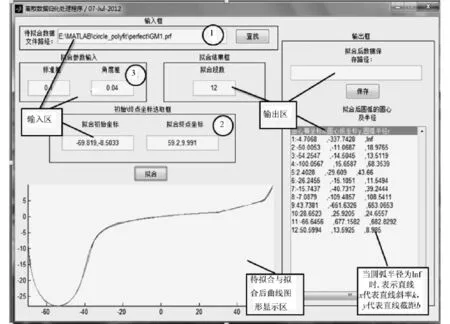
图4 软件外观(图中序号代表输入顺序)
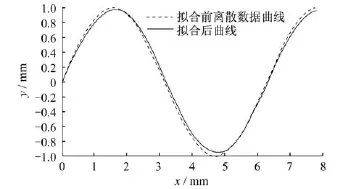
图5 正弦函数拟合情况
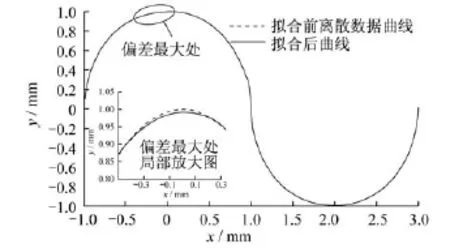
图6 两段相切圆弧拟合情况
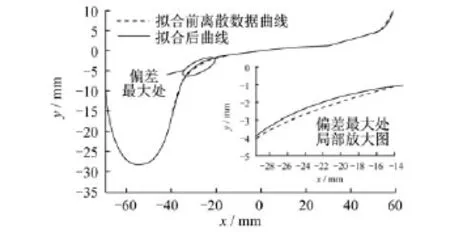
图7 踏面数据的拟合情况
从图8及图9可以看出,由于存在拟合误差,两曲线存在一定的区别,但误差不是很大。为了进一步提高相似度,保证动力学性能,可选择中间的轮轨踏面区域进行拟合。本软件含有拟合区域选择功能。
选择拟合区域,同时减小标准差与角度差的值后进行拟合,结果如图10。将图10与图7进行对比,可明显看出此拟合效果更好,与原离散数据得到的动力学效果更加相近。

图8 轮径差曲线对比
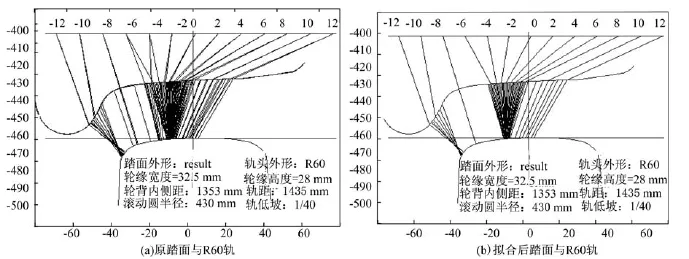
图9 轮轨接触关系对比
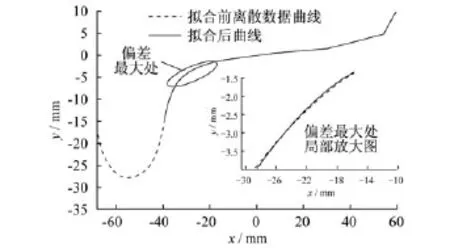
图10 选择拟合区域拟合结果
图11为选择拟合区域前后误差对比,可以看到,选择有特殊精度要求的踏面区域进行拟合,其法向误差显著降低。
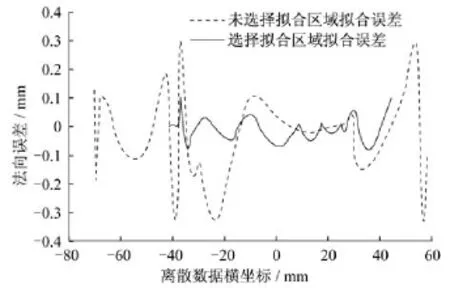
图11 选择拟合区域前后曲线的法向偏差
5 结语
本文提出了用于轨道交通车辆踏面外形的离散点圆弧曲线和直线综合拟合方法,并基于该方法研制了拟合程序。其能通过给定两个精度控制参数,保证拟合精度和拟合后的段数。该方法的实现对于以离散点表达的设计方法的实际工程化应用具有重要意义,方便了不落轮车床的数据输入,也方便了外形的分析研究和规格化表达。
本软件基于MATLAB平台编写,能快速得出拟合结果,给出拟合曲线和曲线参数,包括圆心坐标及交点等信息,并含轮轨接触计算功能,即时分析对比拟合前后的轮轨几何匹配结果,以便最终控制轮轨的外形设计。
[1] 钟晓波,沈钢.高速列车车轮踏面外形优化设计[J].同济大学学报:自然科学版,2011,39(5):710.
[2] 张建霞,苏建辉.多项式数据拟合在La b VIEW中的应用[J].大观周刊,2011(46):37.
[3] 李丽丹.基于MATLAB的离散数据最小二乘拟合[J].辽宁工程技术大学学报,2011,30(z1):202.
[4] 李根强.基于三次样条插值的采样数据光滑曲线形成法[J].计算技术与自动化,2001,20(1):59.
[5] 梁锡坤.基于小波函数的数据拟合方法[J].计算机应用与软件,2003,20(4):3.
[6] 张晓芳.基于有理函数的数据拟合方法[J].电脑与信息技术,2005,13(3):8.
[7] 习胜丰.数据拟合程序的研究与应用[J].浙江工业大学学报,2003,31(5):586.
[8] 虞铭财,杨勋年,汪国昭.整体最优双圆弧拟合[J].高校应用数学学报:A辑,2004,19(2):225.
[9] 梁立,肖飞,郜松.最佳模型拟合的并行算法[J].计算机科学,2007,34(6):294.
Data Processing for Wheel/Rail Profile Measurement
Chen Guofeng,Wang Jie,Zhong Xiaobo,Shen Gang
For the design of the treadin a given error range,the analgorithm is proposed,which fits the discrete data to arc and line,then a computer programis developed,by which the fitting arc and line can be easily used in practical engineering.Several examples verify the simplicity,feasibility and practicability of the fitting method,it is suitable for data entry and standardized management in CNC machine tools.
vehide tread fitting;profile measurement;data processing
U 260.331+.1
2012-09-04)

