CSRT与CST气动外形参数化方法对比

关晓辉，宋笔锋，李占科

（西北工业大学 航空学院，西安 710072）

0 引 言

外形参数化是气动外形设计和优化的第一步，并且对优化过程有着十分重要的影响。由于搜索设计空间的计算量随着设计参数的增加而呈指数增长，参数化过程应使用尽可能少的设计参数来表示几何外形，以降低优化过程的计算量［1－3］。

Kufan和Bussoletti提出用类别形状函数变换（Class Shape Transformation，CST）来表示飞行器的几何外形。这种参数化表示方法使用一个类别函数（Class Function）和一个形状函数（Shape Function）表示飞行器的几何外形，具有参数少和精度高的优点，并且在处理一些重要的设计参数（如翼型前缘半径、尾锥角和后缘厚度等）时十分直观方便［4－6］。但是在对CST参数化方法进行研究的过程中，人们发现这种参数化方法由于使用Bernstein多项式进行形状函数的定义，不具有局部特性，任何一部分局部外形的改变都会造成其它部位的外形变化。另外，表示复杂几何外形时需要使用高阶的Bernstein多项式定义形状函数，但是过高阶的Bernstein多项式会造成CST参数化过程的病态化，从而明显降低表示精度［7］。

Straathof等提出使用具有局部支撑性的B样条基函数对经典的CST参数化方法进行改进，增加了一个由B样条基函数加权和表示的修正函数（Refinement Function），从而得到类别形状修正函数变换法（Class Shape Refinement Transformation，CSRT），并指出这种新型的参数化方法可以用于二级优化过程中。和CST参数化方法相比，CSRT参数化方法具备了几何外形的局部修改能力，但同时也增加了参数数量和相应的计算量［8－9］。

本文对以上两种参数化方法进行对比研究，并使用CSRT方法对超声速机翼进行外形参数化，以此为基础进行以激波阻力最小为目标的有约束二级优化。本文的研究对全面认识CSRT参数化方法和优化超声速客机的外形设计具有一定的参考价值。

1 基本原理

在进行任何气动外形优化计算之前，需要将相关的几何外形使用有限数量的参数表示出来。CSRT参数化方法是由CST参数化方法发展而来的。CST参数化方法使用公式（1）表示后缘封闭的二维翼型：

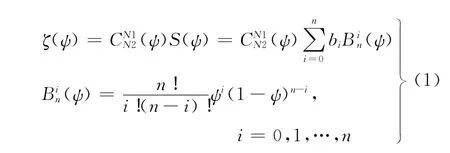
式（1）中，ζ＝z／c，ψ＝x／c，x和z分别为翼型的x轴和z轴的坐标值，c为翼型弦长。（ψ）＝ψN1（1－ψ）N2是类别函数，确定CST参数化方法所表示的几何形状的种类。随着N1和N2的取值不同，类别函数所表示的外形类别是不同的，如N1和N2都为1.0时，类别函数表示双圆弧翼型；当N1＝0.5而N2＝1.0时，类别函数表示类似NACA系列的圆头尖尾翼型；当N1和N2都是0.75时，类别函数表示Sears－Haack旋成体的半径分布。（ψ）是由n阶Bernstein多项式）加权和定义的形状函数，如式（2）所示，它可以将翼型分解为n＋1个分翼型ζi（ψ）加权和的形式。通过调整各个分翼型的权重值bi，可以得到不同的参数向量b，CST参数化方法可以表示不同形状的翼型。如图1所示，定义的圆头尖尾翼型使用3阶Bernstein多项式进行CST参数化分解，可以表示为4个分翼型之和的形式。

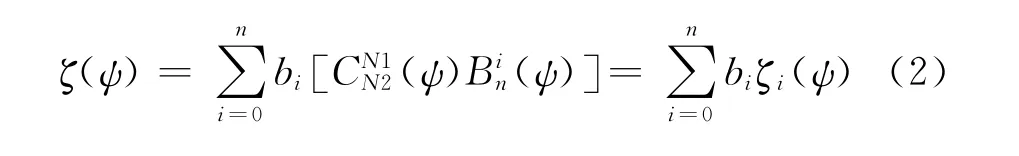
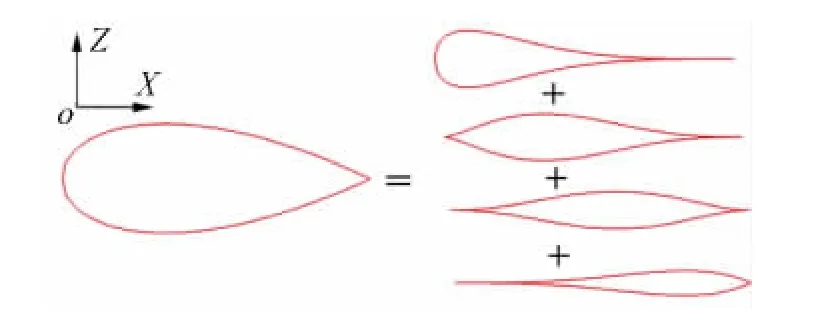
图1 翼型的CST参数化分解Fig.1 CST parametric decomposition of the airfoil

当b＝1时，由Bernstein多项式的性质可以得到S（ψ）＝1，称为单位形状函数，相应的翼型为单位翼型，即类别函数表示的基本翼型。研究表明，由于Bernstein基函数的整体性，如式（1）的这种类似Bezier曲线形式的形状函数定义使得CST参数化方法不具有局部性质，且设计参数的增加必然导致Bernstein多项式阶数的增加，从而导致病态的CST参数化过程，降低表示精度。

CSRT参数化方法利用了B样条基函数局部支撑性的特点，在CST方法的式（1）基础上增加了一个由m＋1个k次B样条基函数加权和定义的修正函数来克服以上缺点［10］。

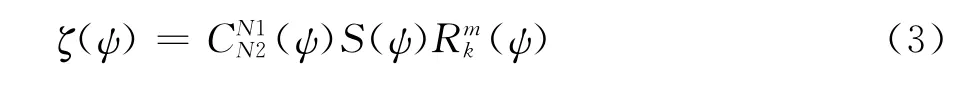
式（3）中修正函数定义为：

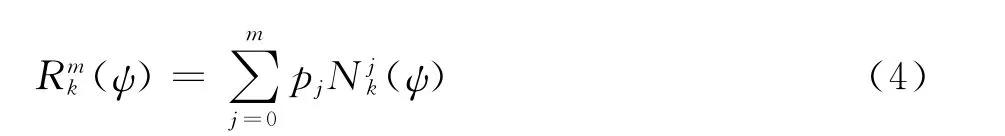
其中，pj（j＝0，1，2，…，m）为引进的修正函数权重因子，组成m＋1阶参数向量p。k次B样条基函数（ψ）是定义在节点向量T＝（t0，t1，…，tm＋k＋1）上的分段多项式，其值可使用de Boor－Cox递推定义公式进行确定［11］：

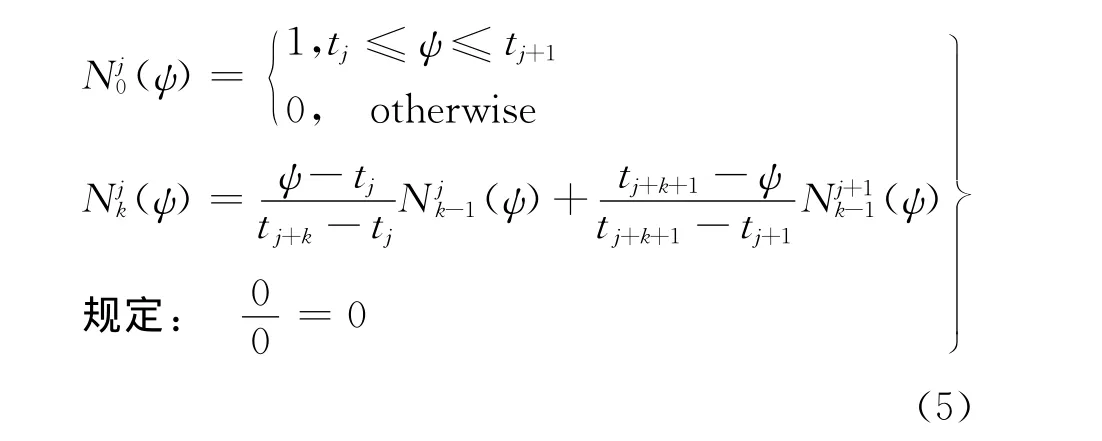
2 表示精度

使用CSRT方法进行几何外形参数化时，需要先确定n＋1个Bernstein多项式的参数向量b，即先进行CST参数化；再确定m＋1个B样条基函数的参数向量p。如图2所示，是使用CSRT方法对RAE2822翼型进行表示的过程中得到的形状对比。

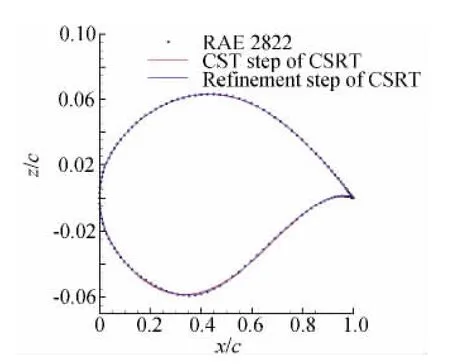
图2 CSRT方法对RAE2822翼型的参数化表示Fig.2 CSRT parametric representation of RAE2822airfoil

图2中的CST参数化使用的Bernstein多项式阶数（Bernstein Polynomial Order，BPO）为3，修正函数为5个2次B样条基函数的加权和R42（ψ）。从图2可以看出，3阶CST方法使用4个参数，对翼型上表面的表示十分精确，但是对更为复杂的下表面曲线有较大的表示误差。修正函数使用5个参数主要对下表面的曲线进行了修形，使其更加接近目标翼型曲线。

如图3所示，是上下表面都使用9个参数的CSRT方法两步计算过程的误差与相同参数数量的8阶CST方法的误差对比。从图中可以看出，CSRT方法通过修正函数获得了局部外形修改能力，但是由于其同时使用了Bernstein多项式和B样条基函数进行参数化计算，有限的参数需要在两步计算过程中进行分配，导致每一步计算未达到其最佳的精度水平。所以在参数数量较少时，CSRT参数化方法的表示精度却不及使用相同参数数量CST方法。

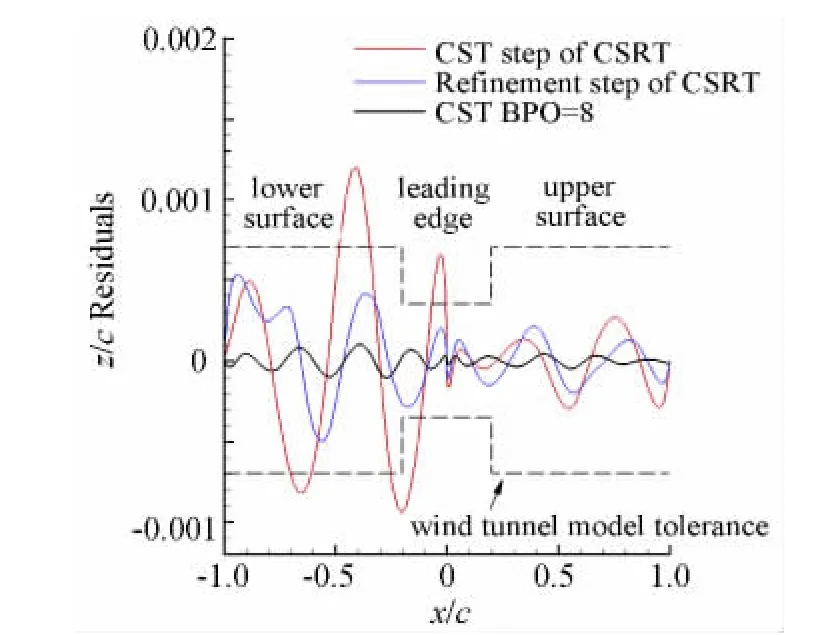
图3 CSRT方法与CST方法的表示误差Fig.3 Residual comparisons of CSRT and CST methods

在参数数量较少时，CSRT方法的表示精度不如CST方法那样高，但是由于其在一定程度上继承了CST方法参数少精度高的特点，所以和其它参数化方法相比，CSRT方法还是有较为明显的精度优势。如图4所示，为保持翼型上下表面都使用9个参数，共18个参数，使用CSRT方法、B样条方法和Hicks－Henne方法对RAE2822翼型进行最小二乘逼近的表示误差对比。在使用B样条方法对翼型进行最小二乘逼近时，计算得到的误差定义为同一参数坐标下原翼型点与样条曲线上点的直线距离，故图4所示的B样条曲线表示误差为非负值。从图4可以看出，在上下表面都使用9个参数的情况下，只有CSRT方法在翼型各个区域的表示精度都能够满足风洞模型的精度要求。B样条方法在其它翼型区域的表示精度很高，但是未能精确表示翼型的前缘形状；Hicks－Henne方法对曲线较为复杂的翼型下表面后缘的表示精度较差。

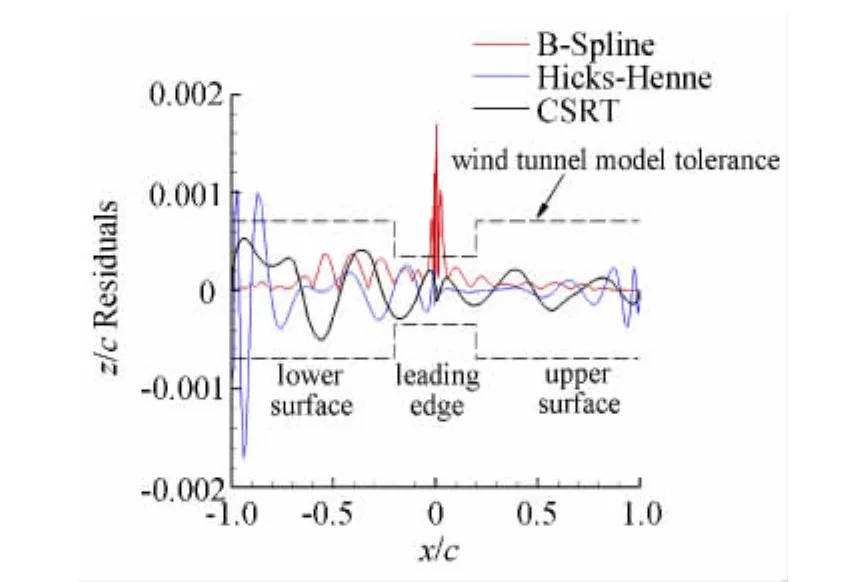
图4 不同参数化方法对RAE2822翼型的表示误差Fig.4 Residual comparisons of different parametric methods

3 单值性

CSRT方法的参数化过程是先确定Bernstein多项式的参数向量b，即进行CST参数化，在此基础上计算B样条基函数的参数向量p。关晓辉等［12］对CST参数化方法的研究表明，过高阶的CST参数化过程系数矩阵是趋于病态的，相应的表示精度也降低了，所以Bernstein多项式应不高于10阶。本文对CSRT参数化方法的单值性研究主要集中在B样条基函数参数向量p的确定过程中。

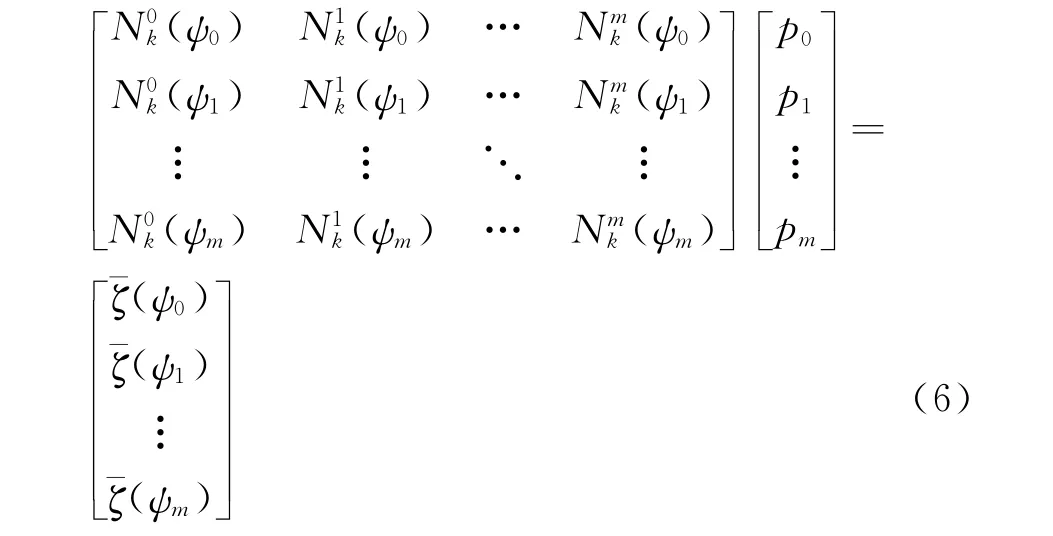
线性系统（6）的系数矩阵记为M，其条件数直接影响线性方程组的性态。取ψj在［0.05，0.95］上平均分布，令N1＝0.5，N2＝1.0，k＝2，如图5所示，为式（6）的系数矩阵M的条件数与CST参数化方法系数矩阵条件数随参数数量增加而变化的对比。从图中可以看出随着参数数量的增加，虽然CSRT方法系数矩阵的谱条件数也在增长，但远小于CST方法系数矩阵的条件数的增长速率。故在一定范围内增加CSRT方法中B样条基函数的参数数量，不仅增强了参数化方法的局部外形修改能力，且不会引起如高阶CST方法那样严重的病态问题。其它ψi分布情况的计算也能得到相同的结论。

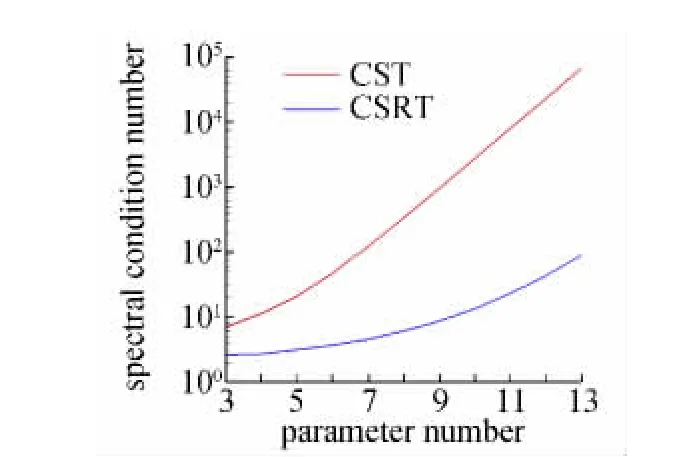
图5 参数化矩阵的条件数Fig.5 Condition number of parameterization matrix

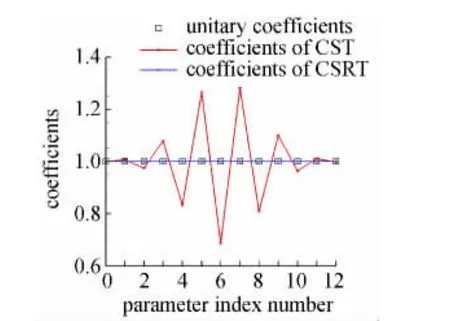
图6 单位翼型的三组参数Fig.6 Three sets of parameters of unit airfoil

从图6中可以看出，由于高阶CST方法的病态化，其单值性变差，计算得到参数向量与单位参数向量差别很大，这就导致两组截然不同的参数确定的几何外形却十分相似（拟合的均方根误差只有6.66×10－5）。在这种情况下任何基于梯度的优化算法性能都会大大降低。CSRT方法得到的B样条基函数参数向量十分接近单位参数向量，没有单值性变差的问题。

由以上结果可以看出，在使用CSRT参数化方法进行参数化表示时，应该合理的分配Bernstein多项式和B样条基函数的参数数量，使参数化过程既具有满意的表示精度，又有灵活的局部外形修改能力。如果要增加参数数量以表示较为复杂的外形，或提高表示精度，在Bernstein多项式的阶数已经较高的情况下，可以适当增加B样条基函数的参数数量，而不必担心参数化过程的病态化。

三维的CSRT和CST参数化方法对几何外形的表示与二维外形的表示过程相似，只是需要增加一个方向上的分解与计算［13］，本文二维的条件下所得到的结论推广到三维的条件下仍然有效。

与CST参数化方法相比，CSRT方法由于增加了额外的修正函数，如果以相同的精度表示几何外形，需要使用更多的参数，这样也增加了设计问题的计算量。但是修正函数使参数化方法具有了处理局部外形的能力，相应的可以在CSRT方法的基础上进行二级外形优化，即第一级整体优化确定Bernstein多项式的参数向量，第二级局部优化确定B样条基函数的参数向量，对整体优化所得到的外形形状进行局部修形［14］。

4 超声速机翼外形二级优化

本文使用CSRT和CST参数化方法对超声速客机机翼进行参数化表示，并使用远场组元激波阻力优化算法对其进行零升激波阻力优化［15－16］。超声速客机翼身组合体平面形状如图7所示。机翼采用中等展弦比的原始机翼与前伸的很小展弦比的边条组合而成的双后掠机翼，这种平面形状的机翼既可能在超声速也在亚声速时获得良好的气动特性［17］。

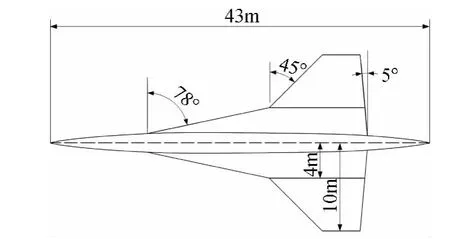
图7 翼身组合体模型平面形状Fig.7 Planform of the supersonic transport wing－body model

机翼零升激波阻力优化过程中，机身形状固定不变，所以机身采用长度43m，最大半径1.3m 的Sears－Haack旋成体，使其激波阻力尽可能的小。

三维CST参数化分解通过将机翼的展向和弦向的外形变量分别表示为ni阶与nj阶Bernstein多项式加权和的方法，把整个机翼分解为若干个分机翼外形的加权和的形式。CST参数化分解形式的机翼表面坐标如式（7）所示：

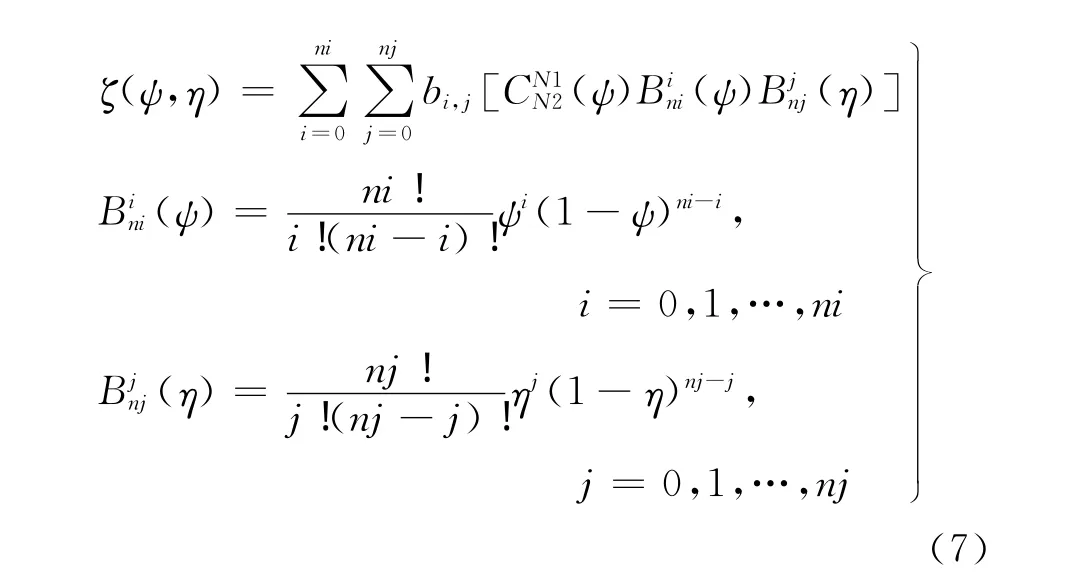
其中η＝2y／b，b为机翼翼展；方括号内表达式为分机翼厚度分布公式；bi，j为弦向第i个Bernstein多项式（ψ）和展向第j个Bernstein多项式（η）所确定的分机翼的权重值。将式（7）中方括号中的分机翼外形表达式单独写出来：

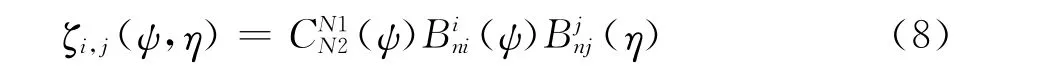
公式（7）可以表示成更加简洁的形式：

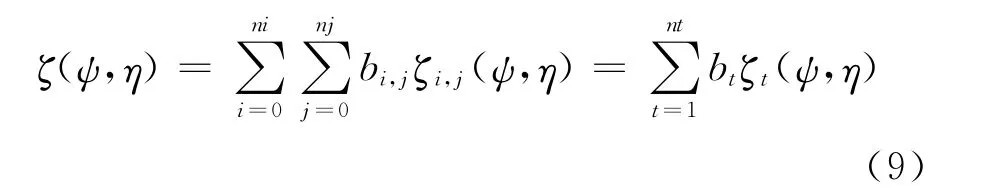
式（9）中，nt为分机翼的总数量，其值为nt＝（ni＋1）（nj＋1）。为方便书写和表示，分机翼的双下标（i，j）可以转换为单下标t，二者之间转换关系为：

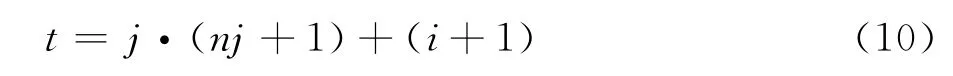
如图8所示，在展向和弦向都使用3阶Bernstein多项式对机翼进行三维CST参数化分解，整个机翼可以表示成16个具有不同厚度分布的分机翼之和的形式。

为了进行第二级优化，还需要使用B样条基函数对机翼进行参数化分解。CSRT对机翼的第二步参数化计算过程与第一步CST参数化类似，所不同的是把Bernstein多项式换成了B样条基函数。

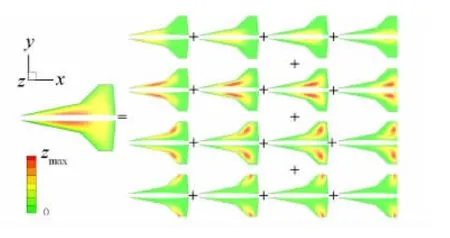
图8 机翼的CST参数化分解Fig.8 CST parametric decomposition of the wing

表1 优化结果Table 1 Optimized results

从表1可以看出，使用36个参数的CST方法结合FCE算法进行的单级整体优化计算可以使超声速翼身组合体零升激波阻力系数从0.00721降低到0.00486，降低32.6%。使用相同参数数量的CSRT方法结合FCE算法进行两级优化计算时，第一级整体优化使翼身组合体的零升激波阻力系数降低到0.00504，在此基础上的第二级局部优化使零升激波阻力系数进一步降低到0.00471，与原外形相比，优化外形零升激波阻力系数共降低34.7%，优化效果略好于使用CST方法的单级整体优化。

基于CSRT方法优化后的机翼各个展向位置上的翼型与原机翼的初始翼型对比如图9所示。

图9 优化翼型与原翼型对比Fig.9 Comparisons of the optimized and the baseline airfoils

机翼的内翼部分（从翼根到机翼转折处），其翼型的厚度增加，展向位置η＝0.1处翼型相对厚度达到了5.7%，并且最大厚度位置从初始翼型的50%弦长处提前到30%弦长附近。内翼翼型的前缘厚度有很大幅度的增加，由于机翼的内翼边条在Ma＝2.0时是亚声速前缘，这种前缘附近厚度的大幅增加不会导致激波阻力的剧增，并且有效的增加了翼根部分的容积，从而补充了超声速前缘部分翼型变薄以后所减少的容积。翼型的后缘附近的厚度和后缘角有一定程度的增加，从而也加大了机翼根部的容积，但也使翼根后缘的膨胀波强度增大。

机翼的外翼部分（从机翼转折处到翼梢）为超声速前缘，从图9中可以看出，外翼优化翼型不仅相对厚度降低，而且翼型的前后缘附近厚度和闭合角也有很大的减小，这样都有利于减小前缘压缩激波和后缘膨胀波的强度和范围。

在FCE激波阻力优化过程中，只使用超声速面积率对翼身组合体的零升激波阻力进行计算［18］，没有考虑升力和升至阻力，所以本文使用计算流体力学（CFD）中求解无粘性欧拉方程的方法对优化前后翼身组合体的升力和阻力变化进行综合对比，同时对基于CSRT方法的FCE算法的优化计算结果进行检验。设定超声速巡航的海拔16km，在Ma＝2.0来流条件下，优化前后翼身组合体极曲线对比如图10所示。其中升力不为零时的阻力为压差阻力，由激波阻力和升至涡阻力构成，没有考虑摩擦阻力。

从图10中优化前后翼身组合体的极曲线对比可以看出，虽然FCE算法只对零升激波阻力进行优化，但是在升力不为零时其优化效果仍然存在，只是随着升力系数增大，阻力的优化效果在逐渐减弱。对比优化前后升力系数可以看出，优化过程对升力影响较小，升力的变化不大。同时可以看出，FCE算法得到的零升激波阻力系数略大于CFD的计算结果，初始构型零升激波阻力系数比CFD的结果大9.8%，优化构型零升激波阻力系数比CFD的结果大5.1%。这样的结果与超声速面积率只使用马赫数进行零升激波阻力系数计算的局限性以及本文进行FCE优化过程中对翼身组合体进行截面分析和数值计算时的误差都有关系。

图10 优化翼身组合体与初始构型的极曲线对比Fig.10 Drag polar comparisons of optimized wingbody and baseline configuration

零升力的情况下，优化翼身组合体与原翼身组合体的表面压强分布对比如图11所示。从图中可以看出，翼身组合体的机翼经过优化后，其前缘激波的强度有了很明显的降低，并且后缘膨胀波的强度和范围也有较大的减小。

图11 优化翼身组合体与初始构型的压强分布对比Fig.11 Pressure comparisons of optimized wingbody and baseline configurations

5 结 论

（1）与CST方法相比，CSRT参数化方法由于增加了修正函数，达到一定的表示精度所需要的参数数量也有所增加。即便如此，和其它的参数化方法，如B样条方法和Hicks－Henne方法相比，仍然具有参数少，精度高的明显优势。

（2）随着参数数量的增加，CSRT方法的病态化程度远低于相同参数数量的CST方法。当CSRT方法第一步中的Bernstein多项式阶数由于病态化问题不能再增加时，可以将更多的参数数量分配给第二步中的B样条基函数，提高表示精度和外形局部处理能力，并且不必担心参数化过程的病态化。

（3）由于使用两步法进行外形表示，CSRT参数化方法可以很方便的进行两级外形优化计算。本文的优化算例中，CSRT参数化方法结合FCE超声速翼身组合体激波阻力优化算法大幅降低了超声速客机翼身组合体的激波阻力，其优化效果优于使用相同参数数量的CST参数化方法进行的单级整体优化。CSRT方法在二级外形优化中的应用并不局限于FCE优化算法，使用其它优化算法结合CSRT参数化方法可以进行相似的二级优化计算。

［1］MOUSAVI A，CASTONGUAY P，NADARAJAH S K.Survey of shape parameterization techniques and its effect on threedimensional aerodynamic shape optimization［R］.AIAA－2007－3837，2007.

［2］SAMAREH J A.Survey of shape parameterization techniques for high－fidelity multidisciplinary shape optimization［J］.AIAA Journal，2001，39（5）：877－884.

［3］SRIPAVADKUL V，PADULO M，GUENOV M.A comparison of airfoil shape parameterization techniques for early design optimization［R］.AIAA－2010－9050，2010.

［4］KULFAN B M，BUSSOLETTI J E.“Fundamental”parametric geometry representations for aircraft component shapes［R］.AIAA－2006－6948，2006.

［5］KULFAN B M.Recent extensions and applications of the“CST”universal parametric geometry representation method［R］.AIAA－2007－7709，2007.

［6］KULFAN B M.A universal parametric geometry representation method－ “CST”［R］.AIAA－2007－62，2007.

［7］CEZE M，HAYASHI M，VOLPE E.A Study of the CST Parameterization Characteristics［R］.AIAA－2009－3767，2009.

［8］STRAATHOF M H，van TOOREN M J L，VOSKUIJL M，et al.Development and implementation of a novel parametrization technique for multidisciplinary design initialization［R］.AIAA－2010－3004，2010.

［9］STRAATHOF M H，van TOOREN M J L.Extension to the class－shape－transformation method based on b－splines［J］.AIAA Journal，2011，49（4）：780－790.

［10］STRAATHOF M H，van TOOREN M J L，VOSKUIJL M，et al.Aerodynamic shape parameterisation and optimisation of novel configurations［C］／／Proceedings of the RAeS Aerodynamic Shape Parameterisation and Optimisation of Novel Configurations Conference.London：Royal Aeronautical Soc.，2008：1－14.

［11］LI Y，ZHANG K F，YU J F.Technology and applications of computer aided geometric design［M］.Xi′an：Northwestern Polytechnical University Press，2007.（in Chinese）李原，张开富，余剑锋.计算机辅助几何设计技术及应用［M］，西安：西北工业大学出版社，2007：30－32.

［12］GUAN X H，LI Z K，SONG BF.A study on CST aerodynamic shape parameterization method［J］.ACTA Aeronautica et As－tronautica Sinica，2012，33（4）：625－633.（in Chinese）关晓辉，李占科，宋笔锋.CST气动外形参数化方法研究［J］.航空学报，2012，33（4）：625－633.

［13］STRAATHOF M H.Shape parameterization in aircraft design：a novel method，based on b－splines［D］.Delft：Faculty of Aerospace Engineering，Delft University of Technology，2012.

［14］STRAATHOF M H，van TOOREN M J L.Adjoint optimization of a wing using the CSRT method［R］.AIAA－2011－3804.

［15］KULFAN B M.New supersonic wing far－field composite－element wave－drag optimization method，“FCE”［R］.AIAA－2008－132，2008.

［16］GUAN X H，LI Z K，SONG B F.Exploring optimization of su－personic wing thickness distribution using FCE （Far－field Composite element）method［J］.Journal of Northwestern Polytechnical University，2012，30（2）：169－174.（in Chinese）关晓辉，李占科，宋笔锋.基于FCE方法的超声速机翼厚度分布优化［J］.西北工业大学学报，2012，30（2）：169－174.

［17］BUSHGENS G S.Aerodynamics，stability and controllability of supersonic aircraft［M］.Guo Z，et al，translated.Shanghai：Shanghai Jiao Tong University Press，2009.（in Chinese）BUSHGENS G S.超声速飞机空气动力学和飞行力学［M］.郭桢，等译.上海：上海交通大学出版社，2009.

［18］JONES R T.Theory of wing－body drag at supersonic speeds［R］.NACA－RM－A53H18A，1953.