低速风洞内部流场数值模拟

代 燚，陈作钢，马 宁，任泽斌

（1.上海交通大学 船舶海洋与建筑工程学院，上海 200240；2.上海交通大学 海洋工程国家重点实验室，上海 200030；3.中国空气动力研究与发展中心，绵阳 621000）

0 引 言

风洞是一种能在管道内产生人工可控气流，利用相似原理进行各种空气动力学实验的设备。低速风洞是指试验段气流速度小于130m／s（马赫数小于0.4）的风洞［1］。从20世纪四十年代开始，国外开始建造低速风洞，迄今低速风洞已经得到了很大的发展。计算机信息技术的迅速发展推动了计算机与风洞的一体化，风洞的试验能力得到了极大提升，获取的信息量增多，试验数据质量明显提高，试验费用下降［2］。技术进步导致试验市场对于风洞性能的要求逐步提高，那些性能差、效率低的风洞必将被逐步淘汰。

风洞的气动设计主要依靠经验公式。随着计算流体力学（Computational Fluid Dynamics，CFD）的快速发展，CFD方法已开始用于风洞试验结果对比及流动机理解释等方面，数值风洞的研究与应用也取得了很大的进展［3－4］，在结构风工程研究中具有战略意义，其长期目标是用计算机部分甚至全部代替风洞。建筑结构三维非定常风荷载数值模拟是数值风洞的主要研究内容之一，基于CFD的风洞气动设计及优化也具有广阔前景。然而，迄今将CFD运用于风洞气动设计的案例还非常少，且仅限于局部辅助设计。在这方面，鲁汶大学的Peter Moonen等［5－6］做出了有益的探索，针对实尺度的Jules Verne全天候风洞，采用一定近似简化后进行了数值模拟，计算结果与试验数据的对比证明了整体模拟具有一定的合理性。

风洞循环水槽作为上海交通大学船舶海洋工程国家实验室（筹）的重要实验设备之一，陈作钢、李金成等［7－9］针对该设备设计上的一些特殊点，采用CFD方法进行了研究，取得了良好效果。其中，多功能风洞是该设施的重要组成部分，针对串列式风洞的大试验段流场品质较差这一问题，通过CFD计算和优化方法进行了辅助设计［7］，研究结果表明优化后的速度均匀性和湍流度指标都得到明显提高。

本文在前期数值研究的基础上，考虑湍流物理模型、网格等影响数值计算的几个关键因素，进一步提高了网格的质量并考虑了阻尼网的整流作用。本文的计算首次全面包含了风洞内部影响流场指标的各要素，如蜂窝器、阻尼网等，因而更加精细地再现了风洞的内部流场。本文的数值模拟预报了各部段的压力损失、流量和风扇功率。数值计算和经验设计法的结果基本一致，计算结果再现了风洞内部的局部流动分离现象，并对地基沉降差造成的风洞同轴度下降引起的流场品质变化进行了定量分析。

1 风洞建模及计算方法

上海交通大学在建的多功能风洞为水平式低速回流型风洞，气动设计布局如图1所示。试验段A（3m×2.5m×16m）最大风速60m／s，试验段B（6m×3.5m×14m）最大风速20m／s。本文采取实尺度的CFD计算模拟风洞内部流场，计算区域如图1所示，包括风扇段（含风扇转子叶片、前支撑、叶轮、止旋片和尾支撑）、各拐角及导流片、试验段、稳定段、扩散段及防分离隔板、收缩段以及蜂窝器、阻尼网、防护网。

采用GAMBIT2.4进行建模和网格生成。对计算域进行分区后生成了混合型网格，为提高计算精度，除一些过渡连接区域外，对包含风扇转子叶片的主体部分绝大部分区域采用结构化网格，网格质量较高，网格单元总数约为550万。为减少网格数量缩短计算时间，将两个稳定段中的蜂窝器的开孔形状由正六边形简化为正方形。

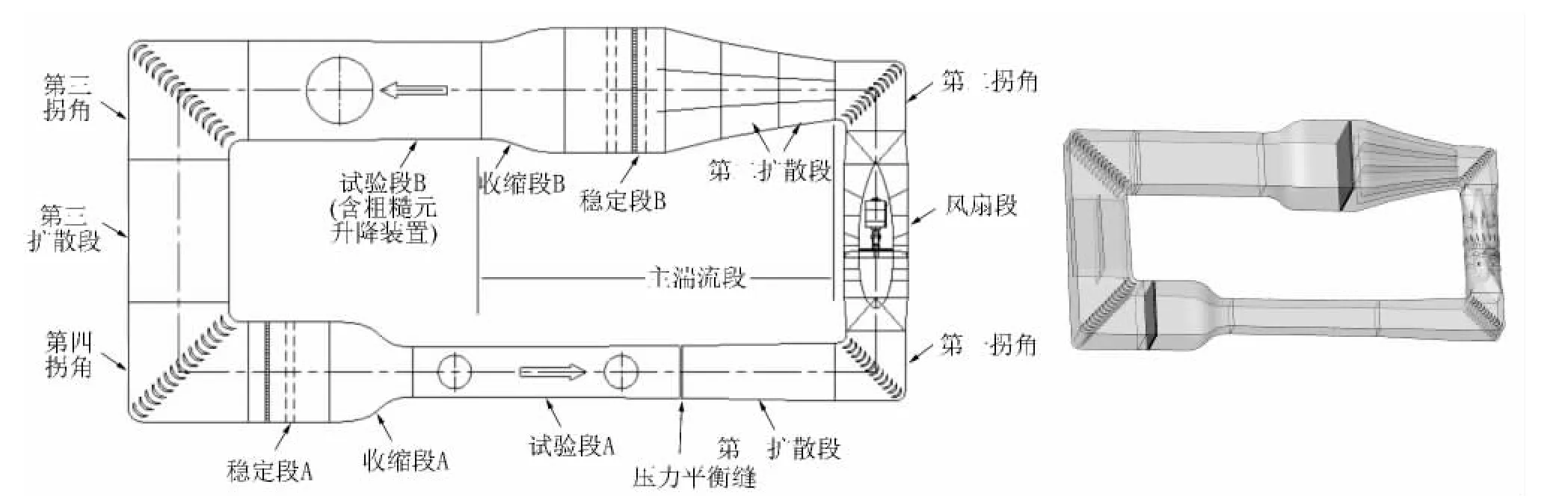
图1 风洞计算模型Fig.1 Diagrammatic sketch of the wind tunnel and computational domain

采用FLUENT6.3进行了流场模拟。用有限体积法求解RANS方程，采用了SST k－ω湍流模式，对近壁流动采用壁函数进行简化，对风扇旋转区域采用MRF（Multiple Reference Frame）方法［10］处理，风扇区域设定旋转速度为600rpm，风扇叶片相对旋转速度为0，风扇段所有壁面采用无滑移壁面。调压缝指定为参考压力，即大气压。SIMPLE法［11］被用于速度与压力之间的耦合，对动量方程采用三阶MUSCL（Monotone Upstream－Centered Schemes for Conservation Laws）［12］格式，对k－ω方程采用二阶上风格式。前期的研究［7－8］中对风扇段进行了数值计算，计算结果和试验数据吻合良好，验证了数值模拟的有效性。

为考察阻尼网对计算结果的影响，本文计算分两种情况：case1不考虑阻尼网与防护网，case2中采用fan边界条件模拟防护网引起的压降，采用porous jump边界条件模拟阻尼网作用。由于空气的动力粘性系数很小，因此porous jump边界条件的压力损失计算不需要考虑Darcy定律。

气流通过阻尼网的压力损失由下式计算：

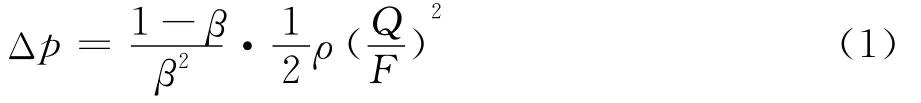
式中，Q为试验段体积流量；F为进入拐角处截面积；β＝（1－d／l）2；d为网丝直径；l为网眼直径。

通过上式计算，稳定段A单层阻尼网的压力损失Δp≈110.49Pa，稳定段B单层阻尼网的压力损失Δp≈31.43Pa。

2 计算结果分析

根据风洞气动设计结果，风扇最大转速600rpm，对应流量为450m3／s，也即试验段A的风速达到最大值60m／s。计算中固定风扇转速为600rpm，得到case1和case2的体积流量分别为447.5m3／s和423.9m3／s，试验段A的风速分别为59.7m／s和56.5m／s，case 2情况比设计值低5.8%。

多目标优化结果［7］表明在第二扩散段宽高方向各加装4块隔板可使试验段B的流场指标接近最优，但考虑到隔板数量的增加显著加大了风洞局部荷重，因此，作为综合考虑后的设计方案，第二扩散段设计成分段扩展，宽高方向各加装2块隔板。case1计算得到的流线如图2所示，第二扩散段和稳定段B中仍存在明显的流动分离，对试验段流场品质产生显著的不利影响。对此，采用在稳定段B中增加阻尼网数量的办法加以解决。图3（a）和（b）分别为case1和case2稳定段B的流线和二者在试验段B转盘中心处的速度分布，该位置距试验段B入口8.5m，为扣除近壁面处边界层的影响，取该截面上宽、高均为70%的矩形区域。图3（a）和图3（b）显示的结果表明流场品质明显提高。case1情况下稳定段的大量逆流影响了试验段的流速均匀性。在case2中采用porous jump边界条件处理方法来实现阻尼网的整流效果，即在动量方程中添加和局部速度平方成正比关系的源项，大幅减小阻尼网所在横截面上的总压变化幅值，使截面上的流速变化幅度得到抑制，从而达到整流的效果。因此case2的计算条件下，尽管在稳定段及其上游仍存在逆流，但经过阻尼网的整流后，试验段B的流场均匀性明显得到提高。

图2 风洞流场流线图Fig.2 Streamlines inside the wind tunnel

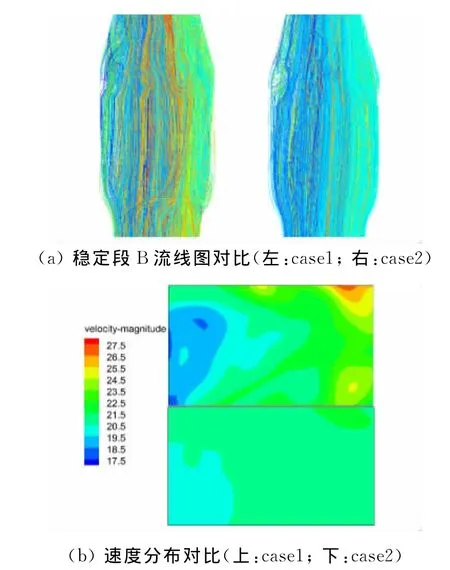
图3 风洞流线及对比Fig.3 Streamlines inside the wind tunnel and comparison

风洞的气动设计必须预测整个风洞消耗的功率，一方面是确定设计的质量，另一方面是选择电机的需要。预测风洞消耗功率的常用方法是：通过理论或者经验公式，计算风洞各段的压力损失，进而得到风洞的总损失。本节将CFD计算得到的风洞各段的压力损失和相关文献［1］给出的经验公式计算结果进行对比，可以发现CFD计算和经验公式各自的长处和不足。

2.1 试验段

试验段的压力损失主要是由壁面摩擦力引起的。根据流体力学公式，由摩擦引起的压力损失为：

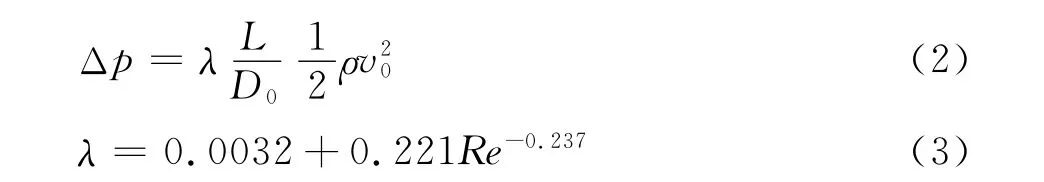
式中，L为试验段长度；D0为试验段水力直径；v0为试验段流速；λ为摩擦损失系数，当1×103＜Re＜1×107时，λ只与Re有关，由式（3）求解。试验段A与B的雷诺数分别约为9.19×106和5.17×106，按式（3）近似求解λ。

CFD计算和经验公式得到的结果对比见表1。除case1中试验段B外，其余结果二者偏差都在3%以下。case1中试验段B与经验公式差距较大的主要原因是试验段B的入口流动不均匀，压力损失增大。

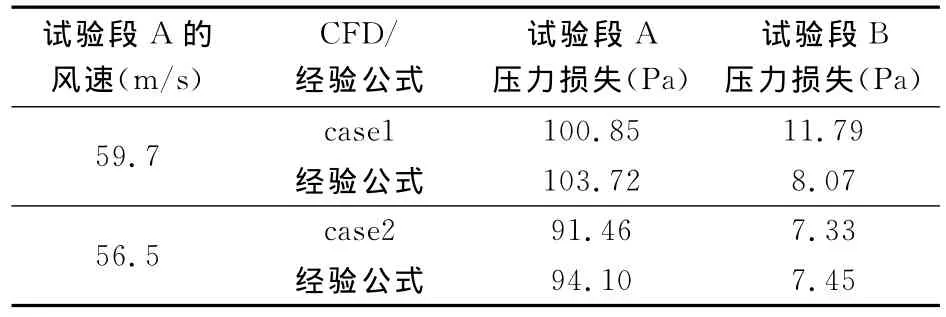
表1 试验段CFD与经验公式压力损失的比较Table 1 Comparison of pressure losses between CFD and empirical formula in the test sections

2.2 扩散段

扩散段在没有流动分离情况下，压力损失可以根据下列经验公式求解：

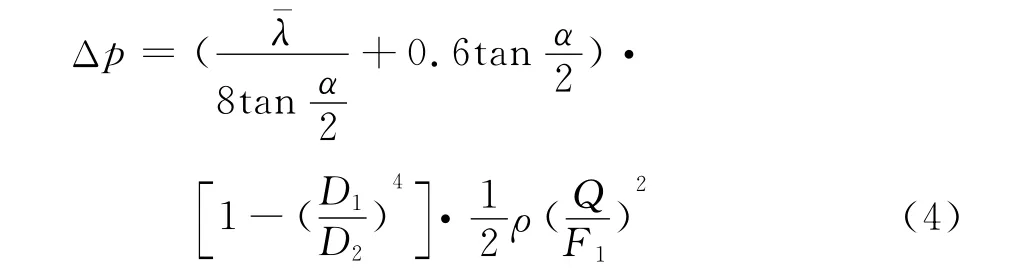
CFD计算结果和经验公式的结果对比如表2所示。二者差距比较大，主要原因在于经验公式是在没有流动分离的条件下推导得到的，然而，如图4所示，计算结果表明在第一扩散段可以观察到明显的流动分离现象，因此该扩散段的压力损失比经验公式的结果高。

通过减少扩散角可抑制第一扩散段的流动分离，但会改变第一拐角的气动轮廓甚至风扇段的直径。考虑到第一扩散段处于试验段A的下游，该段出现流动分离对两个试验段的流场品质都不会出现明显影响，因此没有必有对该处进行大的设计改动。不过，处于试验段B上游的第二扩散段出现的流动分离对试验段B的流场品质会产生较大影响，可考虑在作者前期工作［7］的基础上做进一步气动优化设计。

表2 扩散段CFD与经验公式压力损失的比较Table 2 Comparison of pressure losses between CFD and empirical formula in the divergent section

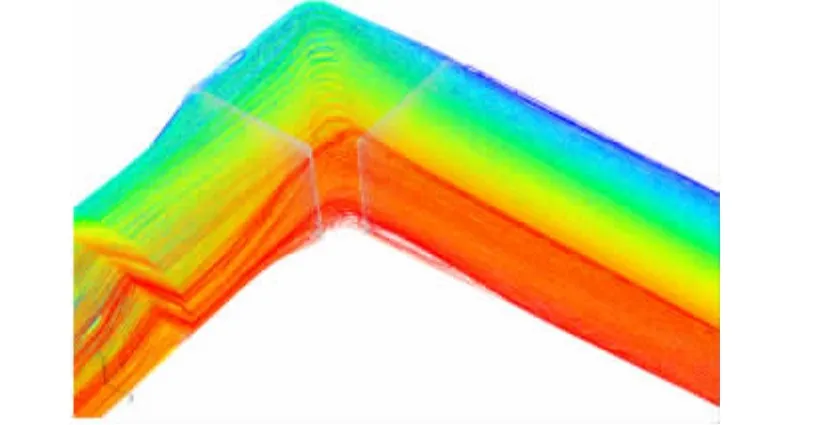
图4 第一扩散段流动分离Fig.4 Flow separation in the NO.1divergent section

2.3 压力损失的整体对比

图2显示了CFD模拟得到的流线，在第二拐角与收缩段B之间存在很多旋涡，这些旋涡跨越各部段，若分别考虑第二拐角、第二扩散段、稳定段B和收缩段B的压力损失将很不准确，因此将他们合并在一起考虑压力损失，称为主湍流段。

将case2中的各段压力损失与试验段A风速同为56.5m／s时的经验设计值［13－14］进行对比，结果列于表3。风洞总损失（除去风扇段）相差216Pa，case2偏小15.3%。差异主要来自第一、三、四拐角和包含第二拐角的主湍流段。对于拐角处的差异一方面可能是由于设计方案的特殊性，各拐角进流与出流截面流动都相对复杂，造成设计中损失估计偏向于保守，此外也必须注意到的是CFD模拟试验段A流速也没有达到60m／s，可以认为偏于保守的估计是合理的。需要指出的是，CFD方法辅助设计还需要进一步与实验进行对比，在今后上海交通大学多功能风洞建成后的流场校测中，将对本文的计算结果进行试验验证，进一步提高CFD模拟精度，探讨与实验相结合的设计方法。

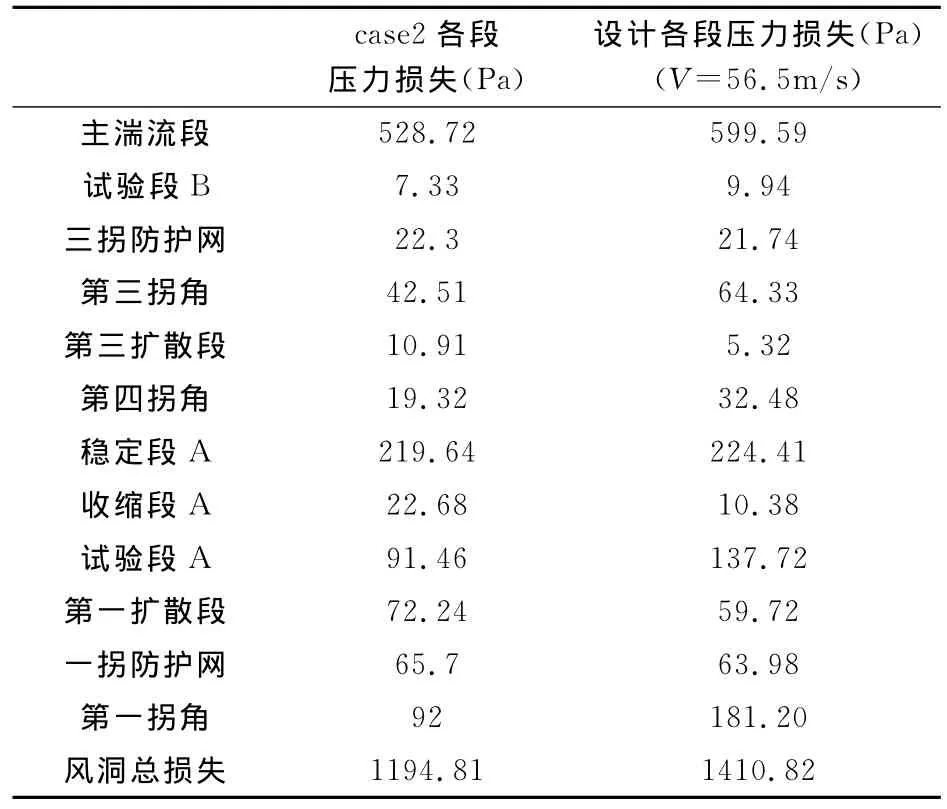
表3 各段压力损失计算结果与经验设计值对比Table 3 Comparison of pressure losses in the sections between CFD and designed values

另外，如图5所示，以压力平衡缝为参考点，二者的总压（静压和动压之和）沿风洞轴线的变化在整体趋势上较为吻合。需要指出的是，经验设计法给出的压力损失是估算的值，跟实际值一定存在一些出入；气动设计时各部段虽然单独设计，但考虑到风洞总体性能，会根据设计经验适当地预留一些余量。

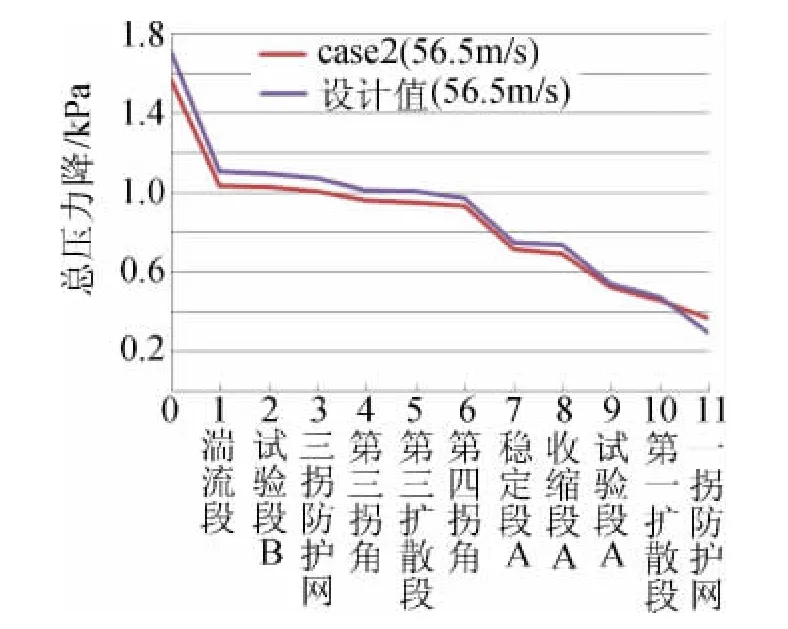
图5 各段压力损失的计算结果与设计值对比Fig.5 Comparison of the pressure losses in the sections between CFD and designed values

表4将case2中的风洞整体、风扇段各项数据与设计值（试验段A风速60m／s）进行对比。CFD计算得到的风扇段总损失较高，导致风扇段效率低于设计的预估值0.75。CFD计算表明在风扇600rpm的转速下，试验段A风速只能达到56.5m／s，设计值风扇扭矩换算为相同风速情况下对比偏差11.5%。风洞实际调试过程中若发现风扇在600rpm时试验段A的风速没有达到60m／s，可以调节风扇叶片的安装角。

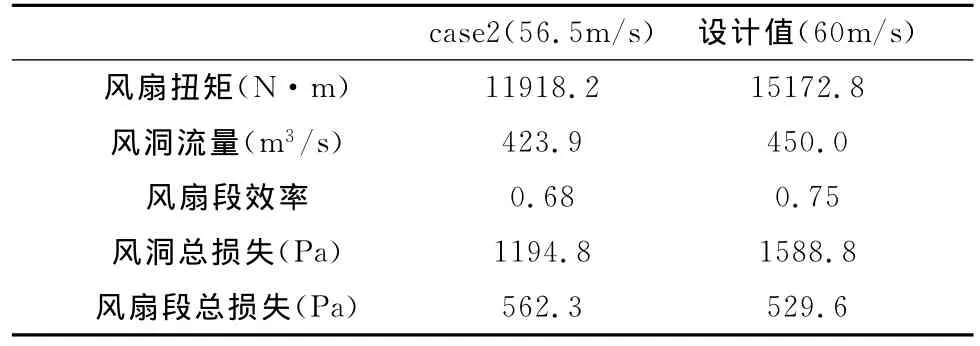
表4 风洞整体参数对比Table 4 Comparison of global parameters in wind tunnel between CFD and designed values

造成CFD计算和设计结果存在一定偏差的原因比较复杂。对经验设计法而言，难以完全预测风洞流场的实际情况，例如流动分离是否发生、风扇段流动的均匀情况等等，而这些状态对风洞的压力损失影响很大；另外，需要特殊设计的部段一般缺乏经验公式或完整理论与之对应，造成预测压力损失比较困难。另一方面，为节省计算时间，本文计算所用网格离壁距离按y＋≈200～300设定，网格单元数控制在550万，流动变化剧烈的地方，如风扇、拐角附近，网格分布密集，而流动变化缓慢的地方，如试验段，则网格分布相对稀疏［15］。按照这一原则，数值再现管道内流动分离具有一定的可信度［16］。不过，由于风洞的尺度较大，结构复杂，在现有的基础上进行加密，计算的精度会有所提高，有可能捕捉到更加细微的流场信息。在计算时间和硬件成本可以接受的条件下，提高网格密度，采用各向异性湍流模式或大涡模拟等方法，将是今后研究值得尝试的方向。

CFD模拟可以揭示风洞内部流场的机理。第一扩散段出现了流动分离现象是设计者难以预知的，在主湍流段，可以清晰地发现流动分离现象相当明显，可以综合考虑气动和结构设计来进行多学科优化，以减小此段的压力损失，提高风洞的性能与运行效率。另外风扇段的压力损失也比较大，设法对其进行改良、降低压力损失也是值得考虑的。

3 同轴度变化对流场指标的影响

保持风洞轴线水平是确保风洞流场指标的要求。然而，同轴度遭到破坏时对流场指标究竟有多大影响却难以通过理论分析或实验方法定量确定。本节采用CFD方法对该问题进行定量分析。

风扇段重量集中，加之动载荷因素，该段基础容易发生较大沉降。为了减少振动传导、防止结构变形，风扇段与其他部段一般采取柔性连接。本节假定风扇段较其他部段的沉降大30mm，如图6所示，在上节的基础上完成建模及CFD计算，表5和表6将计算主要数据结果与case2进行了对比。表5中速度标准差的定义为：

式中，v0是截面平均速度；n为截面中面单元数量。

计算结果显示，风扇段30mm沉降差使风扇段总损失增加3.6%，导致风扇扭矩增大、风扇段效率下降，但是风洞流量并无明显变化。试验段A转盘中心截面速度标准差无变化，图7显示了试验段A的轴向静压梯度，除试验段出入口附近外，该值的绝对值基本小于0.002／m，达到了较高的指标要求。试验段B转盘中心截面速度标准差略有增大，图8将截面速度分布与case2中计算结果进行了对比。结果显示沉降模拟中截面速度最值与case2结果基本相同，但风扇段沉降使截面速度均匀性略有降低。

本节研究表明，若风扇段出现一定程度的沉降差对试验段的流场品质的影响不大。本节提供的方法也可定量分析其他同轴度变化情况对流场的影响。

表5 试验段转盘中心截面速度标准差σ对比Table 5 Comparison of the standard deviation of velocity on the cross section between settlement simulation and case2

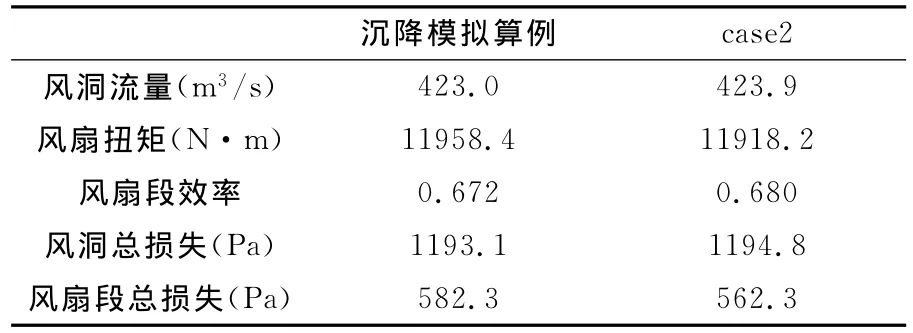
表6 沉降模拟整体参数对比Table 6 Comparison of global parameters between settlement simulation and case2

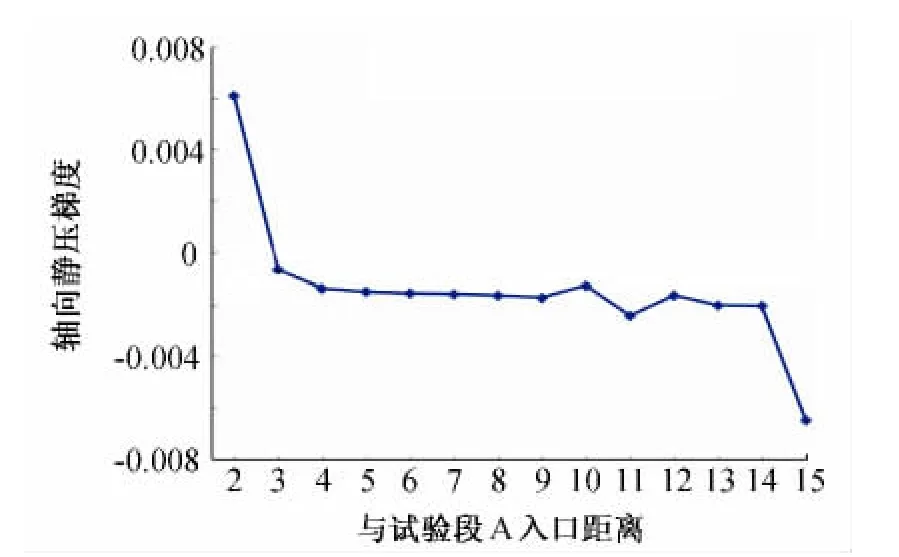
图7 试验段A的轴向静压梯度（m－1）Fig.7 Axial static pressure gradient at the test section（m－1）

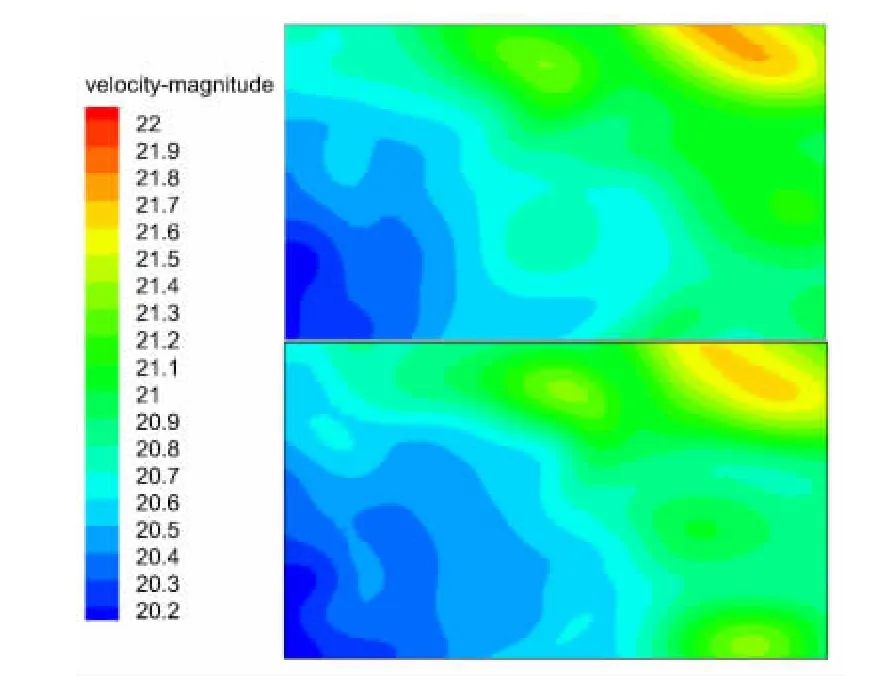
图8 速度分布对比（上：case2；下：沉降模拟）Fig.8 Comparison of the velocity distribution（upper case2；lower：settlement simulation）

4 结论与展望

本文首次完整地实现了对风洞内部流场的数值模拟。通过计算结果对比确认了阻尼网的良好整流效果，体现了在风洞的整体数值模拟中考虑阻尼网的必要性。将数值模拟结果与经验设计法的气动设计结果进行对比发现，数值模拟得到的流量与设计流量差距较小，压力损失在一定程度上较为吻合。数值模拟揭示了风洞内部存在的流动分离现象，为提高风洞的气动性能提供了改进方向。本文对风洞同轴度下降引起的流场品质变化进行了分析，风扇段出现一定程度的沉降差对试验段的流场品质的影响不大。对于风洞的气动设计最为关注的问题，如风洞的主要部段是否发生流动分离、各部段进出口流动是否均匀以及均匀程度等。本文CFD数值模拟能够给出直观的结论。

今后可通过大规模计算，加强与试验相互验证等方法来深化目前的研究，为构建数值风洞奠定基础。

［1］WU R L，WANG Z Y.The principles of wind tunnel design［M］.Beijing：Beijing Publishing House，1985.（in Chinese）伍荣林，王振羽.风洞设计原理［M］.北京：北京出版社，1985.

［2］LI Y R.Research on large low speed wind tunnel about the development，using and testing technology［C］.The Second Modern Experiment Aerodynamics Conference，Harbin，2009.（in Chinese）李友荣.国外大型低速风洞发展、使用及试验技术状况研究［C］.第二届近代实验空气动力学会议论文集，哈尔滨，2009.

［3］ZENG K，WANG C J，HUANG B C，et al.Suggestion and analysis of several key factors in computational wind engineering［J］.ACTA Aerodynamica Sinica，2007，25（4）：504－508.（in Chinese）曾锴，汪从军，黄本才 周大伟.计算风工程中几个关键影响因素的分析与建议［J］.空气动力学学报，2007，25（4）：504－508.

［4］GAO Y，CHOW W K.Numerical studies on air flow around a cube［J］.Journal of Wind Engineering and Industrial Aerodynamics，2005，93：115－135.

［5］MOONEN P，BLOCKEN B，ROELS S，et al.Numerical modeling of the flow conditions in a closed－circuit low－speed wind tunnel［J］.Journal of Wind Engineering and Industrial Aerodynamics，2006，94：699–723.

［6］MOONEN P，BLOCKEN B，CARMELIET J.Indicators for the evaluation of wind tunnel test section flow quality and application to a numerical closed－circuit wind tunnel［J］.Journal of Wind Engineering and Industrial Aerodynamics，2007，95：1289－1314.

［7］CHEN Z G，LI J C，DAI Y，et al.Versatile wind tunnel and CFD－based optimal design［J］.Journal of Experiments in Fluid Mechanics，2012，26（4）：71－76.（in Chinese）陈作钢，李金成，代燚，等.多功能风洞及CFD优化设计［J］.实验流体力学，2012，26（4）：71－76.

［8］LI J C，CHEN Z G，DAI Y.CFD application in design of wind tunnel－circulating water channel［J］.Chinese Journal of Hydrodynamics，2012，27（2）：216－223.（in Chinese）李金成，陈作钢，代燚.CFD在风洞循环水槽中的应用［J］.水动力学研究与进展，2012，27（2）：216－223.

［9］LI J C，CHEN Z G，DAI Y.Design of wind tunnel－circulating water channel assisted with CFD［C］.Proceedings of the 23rdNational Conference on Hydrodynamics and the 10thNational Congress on Hydrodynamics.Xi’an，2011.（in Chinese）李金成，陈作钢，代燚.风洞循环水槽设计的CFD辅助设计［C］.第二十三届全国水动力学研究会暨第十届全国水动力学学术会议文集.西安，2011.

［10］LUO J Y，ISSA R I，GOSMAN A D.Prediction of impeller－induced flows in mixing vessels using multiple frames of reference［C］.IChemE Symposium Series，No.136，Rugby，UK，1994.549－556.

［11］PATANKAR S V.Numerical heat transfer and fluid flow［M］.Washington DC，USA：Hemisphere Publishing Corporation，1980.

［12］Van LEER B.Towards the ultimate conservative difference scheme.V.A second order sequel to Godunov’s method［J］.Comput.Phys.，1979，32（1）：101－136.

［13］HUA S Z，YANG X N.Practical manual of fluid resistance［M］.Beijing：National Defence Industry Press，1985.（in Chinese）华绍曾，杨学宁.实用流体阻力手册［M］.北京：国防工业出版社，1985.

［14］LIU Z C.High and low speed wind tunnel aerodynamic and structural design［M］.Beijing：National Defence Industry Press，2003.（in Chinese）刘政崇.高低速风洞气动与结构设计［M］.北京：国防工业出版社，2003.

［15］LI Q L，YANG Z G.Application of CFD for the design of aeroacoustic wind tunnel［J］.ACTA Aerodynamica Sinica，2009，27（3）：373－377.（in Chinese）李启良，杨志刚.计算流体力学在气动－声学风洞设计中的应用［J］.空气动力学学报，2009，27（3）：373－377.

［16］CHEN Z，KUROKAWA Y，NISHIMOTO H.CFD application on the development of circulating water channel［C］.16th symposium of ISOPE（The International Society of Offshore and Polar Engineers），2006，San Francisco，USA.