水中弹药引信外置涡轮高速旋转两相流动数值仿真

沈德璋，张 合，常自刚，李豪杰，齐献山

（1.中国工程物理研究院 电子工程研究所，绵阳 621900；2.南京理工大学 智能弹药技术国防重点学科实验室，南京 210094；3.海装驻重庆地区军事代表局，重庆 400042）

0 引 言

水中弹药的发射环境同陆上相比有很大差异，引信环境敏感及安全保险控制成为水中弹药引信设计的关键技术。采用头部外置共形涡轮是水下火箭弹引信实现远距离解除保险的一种途径［1］。弹丸水下高速飞行时的涡轮转动情况及流场数据是进行系统参数设计的重要依据。由于模型复杂，且涉及空化等复杂现象，理论分析很难解决此类问题。而试验研究所需周期长，成本高。就水洞模拟试验而言，国内目前仅能达到20m／s以内的流速，水下靶道射击试验则受测量手段局限，能获得的数据十分有限。为预测高速发生空化情况下的涡轮转速，获得涡轮叶片附近压力分布、空化情况、阻力系数等数据，数值仿真是一项经济且实用的方法。随着计算机技术的发展，CFD技术现已成为研究工程流体问题的重要技术手段。

徐长江［2］等提出一种将三维流场数值模拟与电机动力学分析相结合的迭代模拟计算方法，解决了由于引信涡轮电机转速不确定而导致三维流场数值模拟时初始条件无法确定的问题，其针对的是陆上弹药引信用侧进气涡轮，模拟流体为空气的单相流动。关于涡轮机械的仿真研究较多，其中绝大多数为内流问题。王振［3］等应用 S－A、标准k－ε、RNG k－ε、Realizable k－ε以及标准k－ω这五种湍流模型，对涡轮流量传感器内部流场进行了三维数值模拟，其主要针对工业用涡轮流量传感器的工况，不涉及空化情况。黄剑峰［4］等基于欧拉－欧拉方法中均匀多相流假设的混合两相流体无滑移模型，对某混流式水轮机全流道进行了三维定常空化湍流数值模拟。结果表明可以较好地模拟水轮机内真实的有空化发生的多相流动情况。LIU S H、ZHANG L、WU YL［5－6］等研究了采用RNGk－ε湍流模型及Mixure多相流模型模拟混流式水轮机中气液两相湍流流动的方法，认为该方法具有足够的潜力模拟水轮机空化流。SANSONE E［7］等使用非定常的Navier－Stokes方程模拟了横流式水轮机空化及非空化流动，分析了气蚀的动态失速现象及对涡轮性能的影响，认为空化初期出现了叶片失速现象并放大了涡轮脱落涡结构的尺寸。

本文针对弹药在水中高速运行过程，开展涡轮高速旋转且发生空化时的流场两相流动数值仿真研究，模拟不同速度及水深情况下涡轮附近流场的变化，为涡轮优化设计及安全系统参数设计提供支撑。

1 控制方程及计算模型

1.1 控制方程

不可压牛顿流体三维Navier－Stokes控制方程的一般形式：

上述方程对层流和湍流均是适用的。但对于湍流如果直接求解，需要采用对计算机内存和计算速度要求很高的直接模拟方法，目前工程上采用的主要方法是对控制方程做时间平均处理，同时补充反应湍流特性的其他方程，如常用的双方程湍流模型k－ε模型和k－ω 模型。

1.2 旋转坐标系

在旋转坐标系下求解质量守恒以及连续性方程时，动量方程中需要添加流体加速度项。在Fluent中求解旋转坐标系问题时可使用绝对速度或相对速度。两者关系为：

式中：v为绝对速度；vr为相对速度；Ω为旋转角速度；r为旋转坐标系下位置向量。

旋转域中质量守恒方程或者连续性方程可参考下式写成绝对速度或相对速度形式：

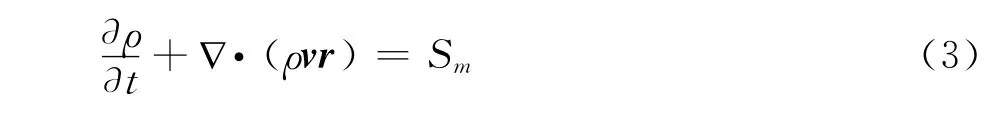
1.3 空化模型

在空化流模拟时，采用Schnerr－Sauer［8］空化模型。Schnerr－Sauer空化模型气相运输控制方程：

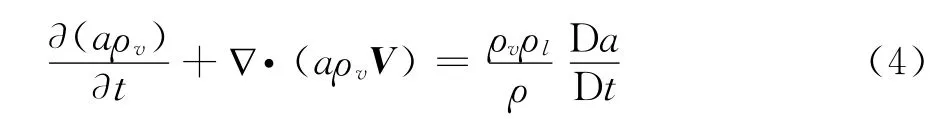
不同于完整空化模型，Schnerr和Sauer推导出了精确的从液体到空泡的净相变率方程：

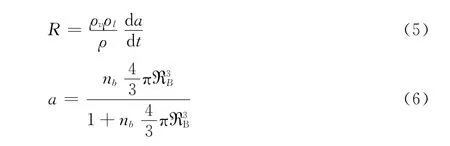
以上两式源于方程：

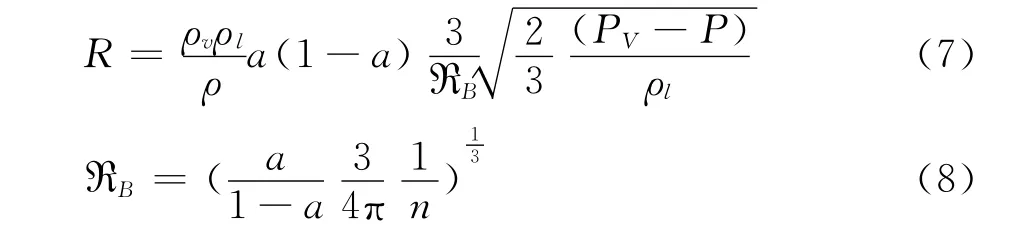
其中，R为质量迁移率，ℜB为气泡半径，v为气相，a为气相体积比，ρv为气相密度，Re和Rc分别为与气泡生长和溃灭相关的质量迁移源项。

2 网格划分及边界条件

2.1 几何模型及网格划分

整个涡轮机构零部件较多，主要包括：小端盖、涡轮、磁体、霍尔器件、连接件、引信体、密封圈、传感器座、紧固圈、轴承等。本文主要分析外部流场的情况，如完全按照某型火箭弹引信原型样机建模，无疑十分复杂，且将对网格划分工作带来极大的困难。因此本文将在计算时对模型做如下简化：

（1）忽略涡轮内部轴承、小磁体、紧固圈等结构，只考虑涡轮外部流场；

（2）原型样机中涡轮与引信体之间的间隙忽略不计；

（3）不考虑涡轮加工工艺中产生的倒角；

（4）忽略涡轮端面用于安装而加工的浅槽。

以涡轮入口叶顶直径φ为参考量，涡轮部分的主要几何参数如表1所示。

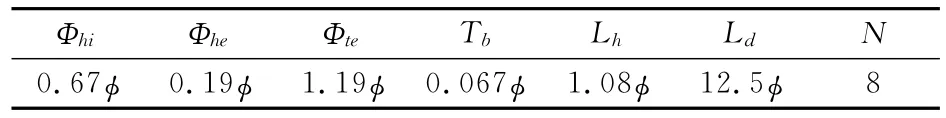
表1 涡轮主要几何参数Table 1 The main geometric parameters of turbine

表中Φhi为入口轮毂直径；Φhe为出口轮毂直径；Φte为出口叶顶直径；Tb为叶片厚度；Lh为轮毂长度；Ld为叶片导程；N为叶片数。

为模拟涡轮旋转，需采用三维数值仿真方法。由于本文涉及的是外部绕流问题，为保证计算结果精度，将涡轮直径φ作为特征尺寸，取整个计算流场长度L＝30φ，直径D＝20φ。

图1 全流场计算区域Fig.1 Flow field computational domain

整个流场主要可分为如图1几个区域，a、d为涡轮前后区，b、c为涡轮区，其中b为旋转区域。整个计算流场体积较大，为控制网格数量，几何模型采用周期性边界，根据涡轮叶片数，取全流场的1／8为计算区域。

计算区域以45°扇形截面沿一定路径进行切割产生，切割路径为叶片前后端连线在扇形角平分线垂直平面内的投影方向。

结构剖分方法如图2所示，图中扇形面SOAB沿上述直线路径平移至面SO′A′B′，该直线投影 OO′与∠AOB平分线OX垂直。

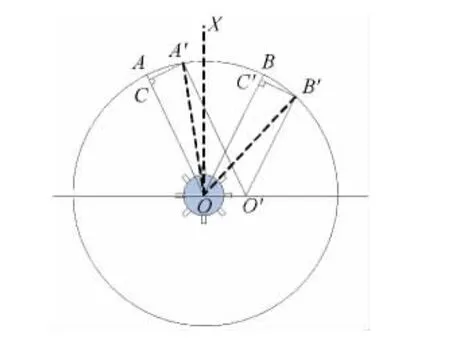
图2 结构剖分方法示意图Fig.2 Schematic diagram of the last division method

平移后边线投影之间的距离A′C＝B′C′，而OA′＝OB′，即有：sin∠AOA′＝sin∠BOB′，∠AOA＝∠BOB′。从而：∠AOB＝∠A′OB′，易得平移后所得圆弧，满足周期性条件。

为划分结构性网格，须保证对边节点数一致的原则。本文涉及的扇形体，对三角形部分Y型剖分，外部圆环部分进行O型剖分，将涡轮部分划分为一个单独的连续体，以便后续使用旋转参考系计算流场旋转的情况。本文对几何模型全部按结构性六面体网格划分，以保证计算精度。为控制计算量，在保证网格质量的同时须控制网格总数。经大量调整，完成网格划分，网格总数约90万。涡轮区域部分网格划分最为复杂，划分完成的涡轮附近部分细节如图3所示。

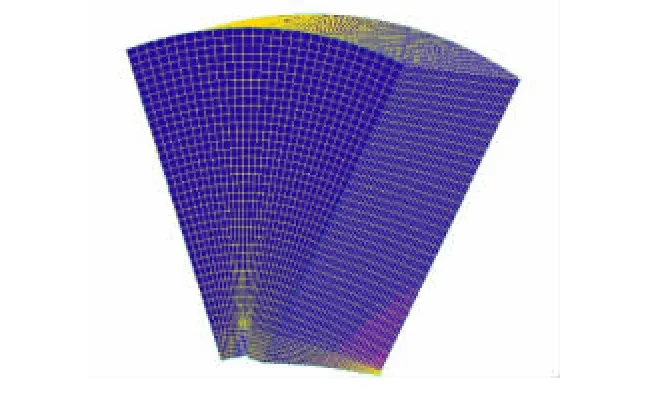
图3 涡轮附近部分细节Fig.3 Details of turbine nearby area

2.2 边界条件及求解算法

采用压力基求解器进行稳态下的定常计算，采用速度入口、压力出口边界，对动区采用旋转坐标系模拟涡轮转动情况。入口速度设置为弹速，出口压力定义为弹丸所处水深位置的压力，假设整个出口压力为恒定值。由于计算前涡轮转速未知，旋转区域转速初始条件确定相对复杂一点。

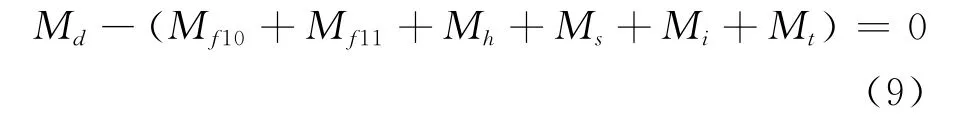
当涡轮在稳定工作状态下时，旋转的角加速度等于0，涡轮力矩平衡方程为：式中Md为水流作用在涡轮叶片上引起的旋转驱动力矩；Mf10和Mf11分别为无负荷时的轴承摩擦力矩和由负荷引起的摩擦力矩。Mh为轮毂端面的粘性摩擦阻力矩；Ms轮毂外表面粘性摩擦阻力矩；Mi为轮毂内表面粘性摩擦阻力矩；Mt为叶片顶端粘性摩擦阻力矩。

其中轴承摩擦力矩采用Palmgren提出轴承摩擦力矩计算公式进行计算［9］，轮毂内表面粘性摩擦阻力矩Mi根据赵学端［10］建立的轮毂内表面粘性摩擦阻力矩公式计算，涡轮驱动力矩、涡轮及叶片表面摩擦力矩均由数值仿真获得。

涡轮转速边界由以下方法确定：（1）根据经验设置初值R0，进行三维数值仿真；（2）根据仿真结果计算驱动力矩及各阻力矩之和，并确定下一次计算的转速值R1；（3）重复步骤（1）～（2），直至上式达到平衡，涡轮叶片力矩之和小于ε，此处取ε＝1×10－6。

湍流模型采用Realizable k－ε模型，近壁处理采用标准壁面函数。多相模拟采用Mmixture多相流模型。压力－速度耦合方程求解算法采用半隐式连接压力方程方法，即SIMPLE算法，该方法是默认算法，稳健性好。单元中心的变量梯度基于单元体的最小二乘法插值（Least Squares Cell Based方法），主要用于多面体网格，与基于节点的格林－高斯格式具有相同的精度和格式。压力插值算法采用PRESTO！格式，该格式主要用于高旋流，压力急剧变化流（如多孔介质、风扇模型等），或剧烈弯曲的区域。对流项的插值采用QUICK格式，此格式适用于四边形／六面体以及混合网格，对旋转流动有用，在均匀网格上能达到三阶精度。

3 计算结果及分析

本文模拟了水深10m、30m及50m条件下，弹速5～100m／s情况下的涡轮高速旋转时的两相流动流场数据。

3.1 空化情况分析

由于外形根据原水下平头弹丸的设计，涡轮表面及叶片部分为弹丸头部最易发生空化的部位。在模拟水深位置为10m情况下，弹速约30m／s时在引信涡轮表面初生空化。不同速度下涡轮部分的空化程度如图4所示。

从图中可以看出，涡轮表面处的空化尺度随弹速增大而增大。弹速30m／s时涡轮表面气相最大体积分数约为34.4%，弹速大于50m／s时涡轮表面部分区域完全空化，气相体积分数最大处接近100%。弹速80m／s时涡轮表面大部分区域发生空化，叶片背面的空化程度比叶片正面更为严重。弹速100m／s的情况下则整个涡轮表面均存在不同程度的空化现象。空化的发生将对涡轮的驱动力矩产生一定影响，进而影响涡轮转动速度。涡轮表面气相体积分数Vp在各区间内的单元数En及所占比例Ep如表2所示。

3.2 压力分布及阻力系数

不同速度下涡轮轮毂表面轴向的表面压力分布曲线如图5所示。

图4 不同弹速下的空化情况Fig.4 The cavitation under different speeds

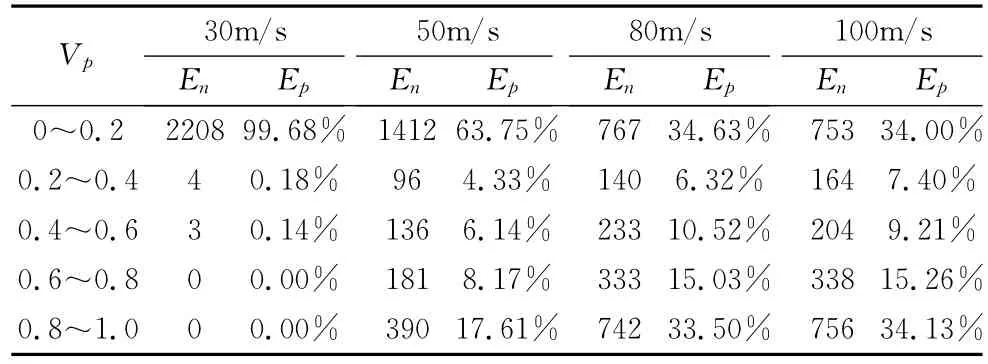
表2 涡轮表面气相体积分数Vp在各区间内的单元数En及所占比例EpTable 2 Unit number En and proportion Ep of turbine surface gas phase volume fraction Vp in each interval

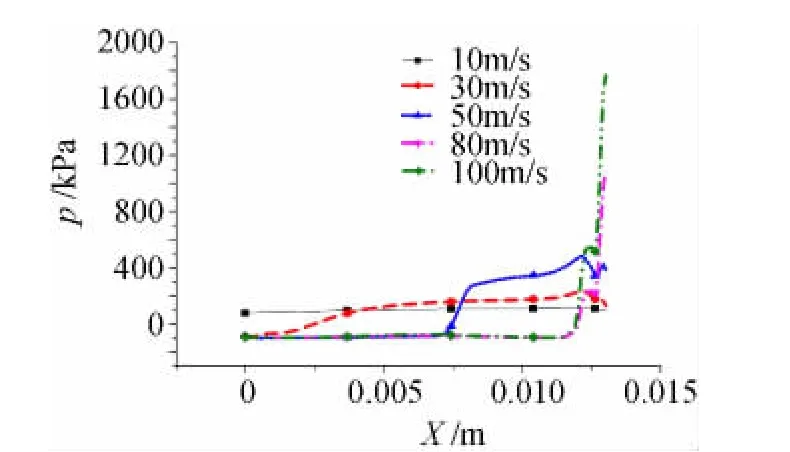
图5 涡轮轮毂表面压力轴向分布Fig.5 Axial pressure distribution of turbine hub surface

涡轮轮毂表面压力在弹速10m／s时变化很小，且均大于0，故不会发生空化。弹速在30m／s以上时，最低压力均为－9.78×104Pa，此即为液态水常温下的饱和蒸汽压。可以看出，随着速度的增大，轮毂表面为最低压力值的轴向距离也在增大，这一趋势正好反映了空化区域尺度的变化，与图4所表达的情况一致。最大压力出现在涡轮后端，随速度增大而增大。

整个弹丸头部轴向阻力系数如表3所示。表中Cpx、Cvx、Ctx分别为头部压力系数、头部粘性阻力系数及头部总阻力系数。

根据表3数据绘制弹丸头部阻力系数曲线如图6所示。

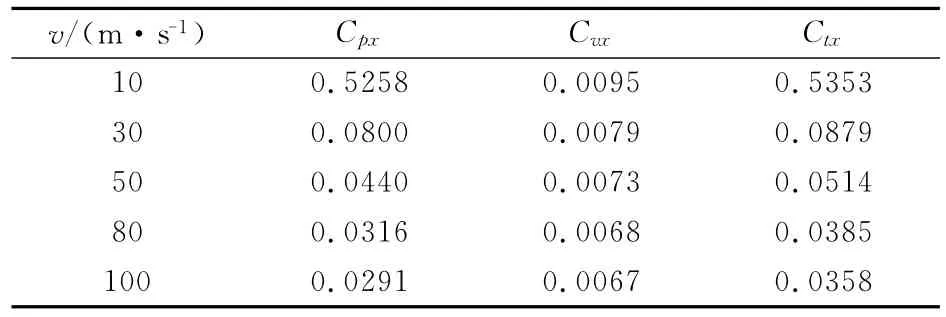
表3 头部轴向阻力系数数据Table 3 Head axial drag coefficients

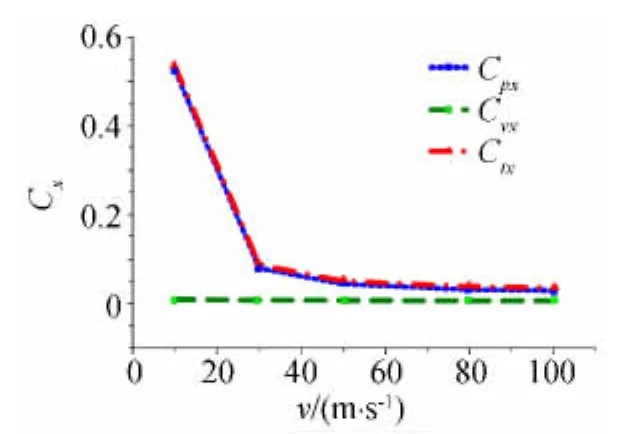
图6 弹丸头部阻力系数曲线Fig.6 Projectile head drag coefficient curve

该弹丸头部装有涡轮，在水下以10m／s速度运动时头部总阻力系数为0.5353，100m／s时的总阻力系数为0.0358，可以看出总阻力系数随速度的增大而减小。10m／s时粘性阻力在总阻力中所占比例为1.8%，随速度增大，粘性阻力的影响逐渐明显，100m／s速度下粘性阻力占总阻力的18.7%。

3.3 涡轮转速计算

通过迭代方法获得了不同水深（10m、30m及50m）及弹速条件下的涡轮转速，部分数据如表4所示。

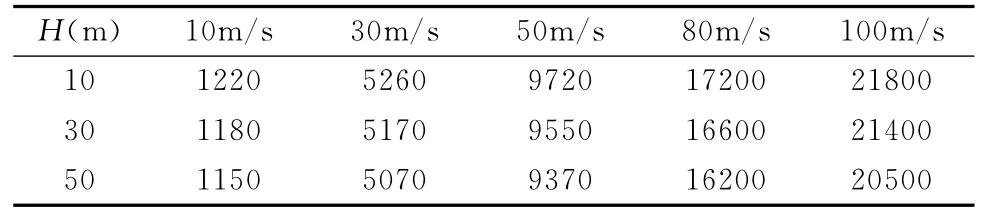
表4 不同水深及速度下的涡轮转速（r／min）Table 4 Turbine rotation speed at different water depths and speeds（unit：r／min）

在10m、30m及50m水深条件下，绘制出涡轮转速与弹速的关系曲线如图7所示。

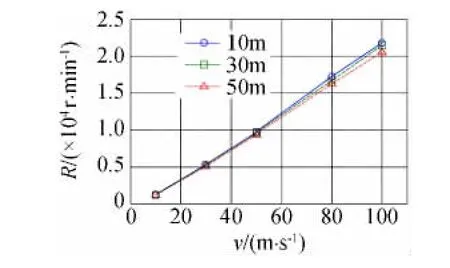
图7 不同水深条件下弹速与涡轮转速关系曲线Fig.7 The relationship curve of projectile speed and turbine rotation speed at different water depths

根据上述曲线可以看出，静压力对涡轮转速存在一定影响。在弹速为100m／s时，50m水深条件下的涡轮转速比10m水深时小约5.96%。

在弹速范围内，涡轮转速与弹速接近为线性关系。对水深10m条件下的弹速与涡轮转速关系曲线采用最小二乘法进行线性拟合，得：y＝230.8x－1454，非线性度γ＝0.998。

4 结 论

由于对高速下涡轮表面的空化情况、弹丸头部阻力系数以及涡轮转速规律没有定量研究结论可供参考，一直以来水中弹药引信涡轮设计及系统参数选取均以经验设计为主。本文通过对某水下火箭弹引信涡轮高速旋转两相流动的三维流场数值仿真，得到以下结论：

（1）引信涡轮表面空化程度随弹速的增加而严重，空化尺度与弹速成正比例关系，弹速30m／s左右时空化初生；

（2）水中弹药的粘性阻力比空气中大很多，弹速100m／s下头部粘性阻力占总阻力的18.7%；

（3）高速下涡轮转速与弹速仍具有较好的线性关系，10m水深条件下的R－v曲线非线性度γ＝0.998；

（4）不同水深条件对涡轮转动有一定影响，文中R－v曲线对于安全系统参数设计、控制解保距离具有一定参考意义。

［1］SHEN D Z，ZHANG H，LI H J.A delay arming technical scheme for underwater rocket fuze based on external conformal turbine［C］.The 2ndInternational Conference on Computer Application and System Modeling，Xiamen，China.2011

［2］XU C J，ZHANG H.Numerical simulation 3－D of flow－field of a turbine alternator with side intake ducts for the fuze coupled［J］.Journal of Projectiles，Rockets，Missiles and Guidance，2006，26（1）：110－113.（in Chinese）徐长江，张合.引信用侧进气涡轮电机三维流场数值模拟［J］.弹箭与制导学报，2006，26（1）：110－113.

［3］WANG Z，ZHANG T，ZHENG D D.Comparison of different turbulence models for numerical simulation of internal flow field of turbine flow sensor［J］.Journal of Tianjin University，2007，40（12）：1447－1451.（in Chinese）王振，张涛，郑丹丹.涡轮流量传感器内部流场数值模拟中湍流模型比较［J］.天津大学学报，2007，40（12）：1447－1451.

［4］HUANG J F，ZHANG L X，YAO J，et al.Numerical simulation of 3D cavitation turbulent flow in francis hydro－turbine passage on mixture modeling technology［J］.Proceedings of the CSEE，2011，31（32）：115－121.（in Chinese）黄剑峰，张立翔，姚激，等.混流式水轮机三维空化湍流场混合数值模拟［J］.中国电机工程学报，2011，31（32）：115－121.

［5］LIU S H，ZHANG L，NISHI M，et al.Cavitating turbulent flow simulation in a francis turbine based on mixture model［J］.Journal of Fluids Engineering，2009，131（5）.

［6］WU Y L，LIU S H，DOU H S，et al.Simulations of unsteady cavitating turbulent flow in a Francis turbine using the RANS method and the improved mixture model of two－phase flows［J］.Engineering with Computers，2011，27（3）：235－250.

［7］SANSONE E，PELLONE C，MAITRE T.Modeling the unsteady cavitating flow in a cross－flow water turbine［J］.Journal of Fluids Engineering，2010，132（7）.

［8］SCHNERR G H，SAUER J.Physical and numerical modeling of unsteady cavitation dynamics［C］.Fourth International Conference on Multiphase Flow，New Orleans.USA，2001.

［9］LIU Z J，HE S Q，LIU H.Antifriction bearing application［M］.Beijing：Mechanic Industry Press，2007，3：650－654.（in Chinese）刘泽九，贺士荃，刘晖.滚动轴承应用［M］.北京：机械工业出版社，2007，3：650－654.

［10］ZHAO X D.Turbine flowmeter mathematical model and optimal design［J］.Academic Journal of Shanghai Mechanic College.1985，（2）：1－15.（in Chinese）赵学端.涡轮流量计数学模型与优化设计［J］.上海机械学院学报，1985，（2）：1－15.

［11］XIA Z F，LUO S，YANG Y.Numerical simulations of propeller slipstream flows using actuator disk theory［J］.ACTA Aerodynamica Sinica，2012，30（2）：219－222.（in Chinese）夏贞锋，罗淞，杨永.基于激励盘理论的螺旋桨滑流数值模拟研究［J］.空气动力学学报，2012，30（2）：219－222.

［12］ZHU M H，YE Z Y，JIN L.Numberical simulation of separation equilibrium of flow around 2D wing configuration at high angle of attack［J］.ACTA Aerodynamica Sinica，2012，30（4）：477－482.（in Chinese）祝明红，叶正寅，金玲.二元翼型大迎角绕流的平衡态（解）的数值研究［J］.空气动力学学报，2012，30（4）：477－482.

［13］WANG Z，ZHANG T，SUN L J.Numerical simulation on turbine flowmeter for measurement of gas－liquid two－phase flow and experiment verification［J］.Journal of Tianjin University，2008，41（11）：1303－1308.（in Chinese）王振，张涛，孙立军.涡轮流量传感器测量气液两相流的数值仿真与实验验证［J］.天津大学学报，2008，41（11）：1303－1308.

［14］WANG Z，ZHANG T，XU Y.Simulation and experiment on tangential type turbine flow sensor for measurement of low flow rate［J］.Journal of Tianjin University，2007，40（9）：1048－1053.（in Chinese）王振，张涛，徐英.测量小流量的切向式涡轮流量传感器的仿真与实验［J］.天津大学学报，2007，40（9）：1048－1053.

［15］WU Y D，OUYANG H，XU K，et al.Numerical investigation on the mechanism of micro tab to the airfoil［J］.ACTA Aerodynamica Sinica，2012，30（6）：786－791.（in Chinese）吴亚东，欧阳华，许坤，等.基于数值方法研究带小插片的翼型的流动机理［J］.空气动力学学报，2012，30（6）：786－791.