亚轨道可重复使用飞行器（SRLV）气动布局优化方法研究

王旭刚，杜 涛，张耐民

（北京宇航系统工程研究所，北京 100076）

0 引 言

亚轨道飞行器（以下简称SRLV）不同于以往的运载火箭、飞船，SRLV一般采用同场或异场返回方式，要具备良好的全速域、宽空域可控飞行能力、大范围机动能力和水平着陆能力，所涉及的气动问题包括了从低速到高超声速空气动力学和稀薄气体动力学的各个领域，SRLV在所有速度范围内都获取优越气动性能的设计难度很大。本文重点开展亚轨道飞行器返场阶段的气动布局优化设计，以优化飞行器总体性能。而机翼无疑是对亚轨道返场气动性能影响最大的部件。但由于机翼设计变量繁多，若采用传统的工程估算方法进行气动性能计算，计算精度难以保证；为保证设计可信度，要求在设计过程中采用高精度模型进行CFD数值计算分析，准确性有保证，但是存在计算量大、耗时长、成本高等问题，难以在工程设计上大规模应用。通过应用代理模型方法，可以结合上述两种方法的优点，解决效率和精确性的统一。

本文针对翼身组合体的SRLV，开展了具有工程实用性的气动布局优化设计技术研究，在既有外形基础上，通过优化实现了气动性能的提升。

1 基于代理模型的SRLV气动布局优化方法

目前国内外基于高保真度CFD计算的气动布局优化技术方面基本还处于理论研究阶段，如基于伴随方法的气动布局优化设计方法［1］。而基于近似模型（代理模型）的优化设计技术日臻成熟，能够满足目前的工程设计条件。其基本思想是用响应面模型来代替目标函数和约束函数进行优化，以降低优化问题规模并缩短优化时间。

本文基于近似模型建立了SRLV气动布局工程优化方法，其优化流程如图1所示。该方法用Kriging响应面模型来近似目标函数和约束函数［2－3］，优化算法采用混合遗传算法，一般遗传算法用于全局搜索，然后再以遗传算法优化结果作为基于梯度的优化算法的起始点进行局部搜索［4］。气动分析采用基于工程估算的变复杂度气动分析方法，变复杂度气动分析模型是对气动工程估算结果与风洞试验或CFD计算结果的插值（或比值）构建响应面模型，以此来提高气动工程估算的保真度。

本文采用代理模型开展了SRLV气动布局工程优化设计，在满足进度要求的条件下，完成了外形的优化，取得了满意的效果。下面首先对设计的主要方法进行介绍。

1.1 代理模型

代理模型是大量的低精度数据，通过响应面等方法，借助少量的高精度数据，来提高模型精度。这一方面的优点是，大幅度降低气动建模的计算量，节省经费和缩短时间，而且模型具有扩展性，可以通过增加高精度数据的数量来提高代理模型的精度，直至与高精度模型一致［4］。代理模型的关键是构造良好修正低精度数据的响应面模型（Response Surface Model）。Kriging模型是一种估计方差最小的无偏估计模型［5］，目前Kriging模型已经成为多学科设计优化中比较有代表性的一种代理模型近似方法。

Kriging模型假设系统的响应值与自变量之间的真实关系可以表示成如下的形式：

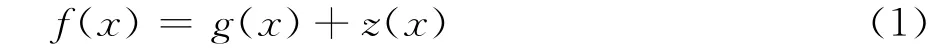
其中g（x）是一个确定性部分，全局地逼近设计空间，称为确定性漂移，一般用多项式表示；z（x）称为涨落，用来产生局部的偏差，进行局部估计。在本文中，将采用基于Kriging模型开发代理模型。

1.2 优化模型

本文涉及计算中采用了遗传算法和序列二次规划法，现分别做简单地介绍。

（a）遗传算法

遗传算法（Genetic Algorithm，简称GA）是模拟生物在自然环境中的遗传和进化过程而形成的一种自适应全局优化概率搜索算法。它起源于20世纪60年代对自然和人工自适应系统的研究，最早由美国密执安大学的Holland教授提出。详细可见参考文献［6］。

遗传算法通过适当的选择机制或采用小生境技术，在一次运行中可以生成大量的非劣解，因此可能搜索到多目标优化问题的Pareto最优解集。

（b）序列二次规划法

二次规划是指目标函数为二次、约束函数为线性的非线性规划，常可利用最优解的K－T条件出发构造有效的解法。将变尺度法用于约束极小化问题，在当前的迭代点xk处，利用目标函数的二次近似和约束函数的一次近似构成一个二次规划，通过求解这一个二次规划获得下一个迭代点xk＋1，这种将求解非线性规划转换为求解一系列二次规划的方法，称为序列二次规划方法。序列二次规划方法（SQP）包括DONLP和NLPQL两种，本文采用的是后者。

1.3 优化流程

优化流程如图1所示。该方法用Kriging响应面模型来近似目标函数和约束函数，优化算法采用混合遗传算法，一般遗传算法用于全局搜索，然后再以遗传算法优化结果作为基于梯度的优化算法的起始点进行局部搜索［6］。气动分析采用基于工程估算的变复杂度气动分析方法，变复杂度气动分析模型是对气动工程估算结果与风洞试验或CFD计算结果的插值（或比值）构建响应面模型，以此来提高气动工程估算的保真度。

图1 SRLV气动布局优化流程Fig.1 Aerodynamic configuration optimization process

2 SRLV气动布局优化设计

2.1 原始布局主要气动参数

为了获得更好的气动性能，需要对原始气动外形开展优化设计，通过调整机翼的安装角、扭转角和后掠角，在不降低升阻比前提下，提高升力系数［7－12］。

图2 原始SRLV气动布局Fig.2 The original SRLV aerodynamic configuration

SRLV机翼安装角为0°，机翼扭转角为0°，后掠角为79.3735°。

计算状态为Ma＝0.8，来流迎角为α＝30°。

依据风洞试验提供的数据，原始外形主要气动特征数据如表1所示。

表1 主要气动特征数据Table 1 The main aerodynamic characteristic data

2.2 气动布局优化问题的定义

优化目标为在保证SRLV基本构型不变的前提下，通过调整机翼的安装角、扭转角和后掠角，在不降低升阻比前提下，提高升力系数。

该问题可以描述为：

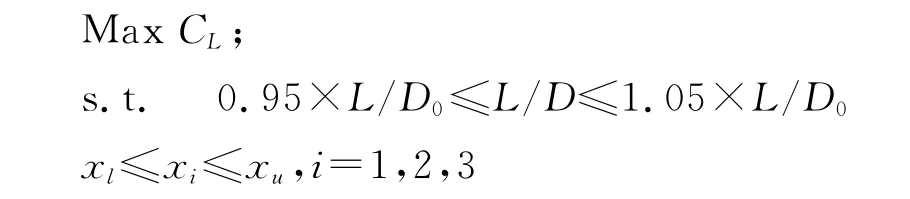
其中CL为升力系数，L／D为升阻比，L／D0为基本型的升阻比，xi为设计变量，xu、xl为设计变量的上下界。

设计变量及其取值范围见表2。

2.3 构造代理模型

（1）试验设计点的产生。对所选的亚轨道飞行器的3个设计变量采用拉丁方试验设计方法来确定外形组合，共30组试验样本点。如表3所示。

表2 亚轨道飞行器气动优化设计变量及取值范围Table 2 The SRLV aerodynamic optimization design variables and the range

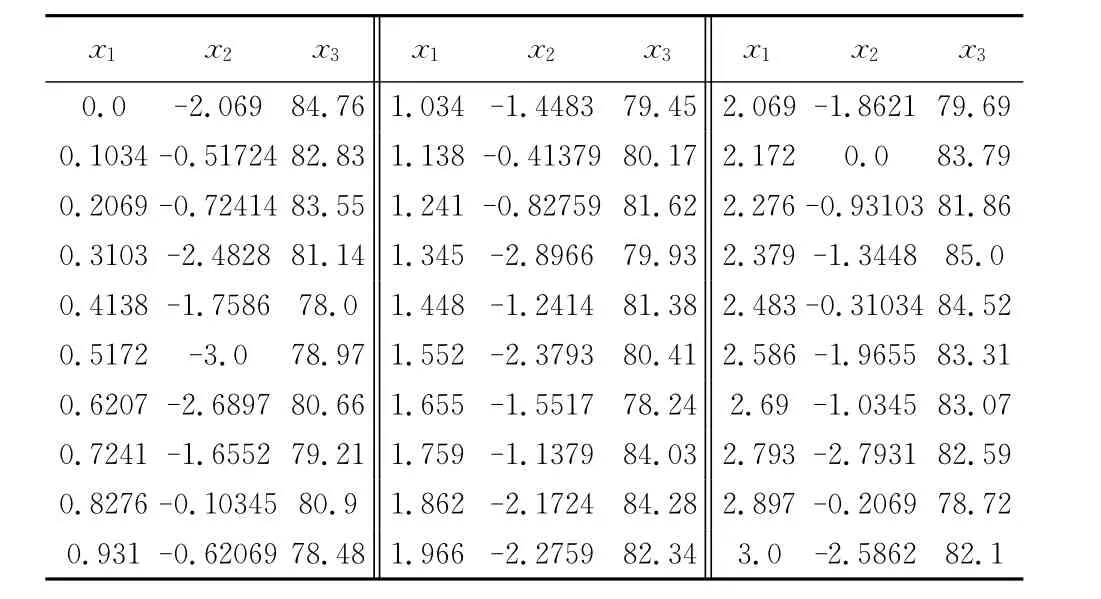
表3 试验设计点Table 3 Design of experiments

（2）建立几何模型。根据拉丁方样本设计方案，建立其对应的几何模型。

（3）气动力系数的计算。快速生成设计方案模型对应的直角网格，进行CFD数值计算，完成流场计算。工程方法估算摩阻和底阻。计算得到L／D和CL。

（4）构建代理模型。应用Kriging方法建立机翼气动分析代理模型，建立设计变量（安装角、扭转角、后掠角）与气动特性（升力系数、升阻比）之间的关系。为了检验代理模型拟合精度，将基本型的CFD计算结果与代理模型拟合结果进行对比，结果如表4。从中可见，代理模型的结果与CFD数值计算结果很接近，表明该代理模型可用。

表4 检验代理模型结果Table 4 The surrogate model test results

2.4 优化结果

为了尽量获得全局最优解，在优化过程采用了无需梯度计算的遗传算法和基于梯度的序列二次规划相结合的策略。即：首先采用遗传算法在整个设计空间内寻找最优解，然后以该最优解为起始点，采用基于梯度的序列二次规划法进一步找到最优解。前者全局寻优能力好，后者局部搜索能力强，二者结合起来使用的效果好。

通过优化搜索得到了优化设计的Pareto解集。同时把选择的优化设计点用CFD方法进行验算，检验代理模型结果的可靠性。如发现精度不够满意，则把最新计算出的结果作为一个新的设计点，一起加入到代理模型中，如此反复，直到结果精度较高。图3给出目标函数空间的Perato解集。本例中，优化四次后得到了比较满意的结果。随后根据设计经验，以及考虑其它专业的非约束性要求，对优化结果进行了合理选择。优化结果及CFD验算结果的比较给出在表5中，从表中可以看到代理模型优化的结果同CFD数值计算得到的结果一致。优化后对应计算流场云图见图4。

图3 目标函数空间的Pareto解集Fig.3 Pareto solution set in objective function space

图4 计算网格和压力分布云图Fig.4 Computational grid and pressure contour

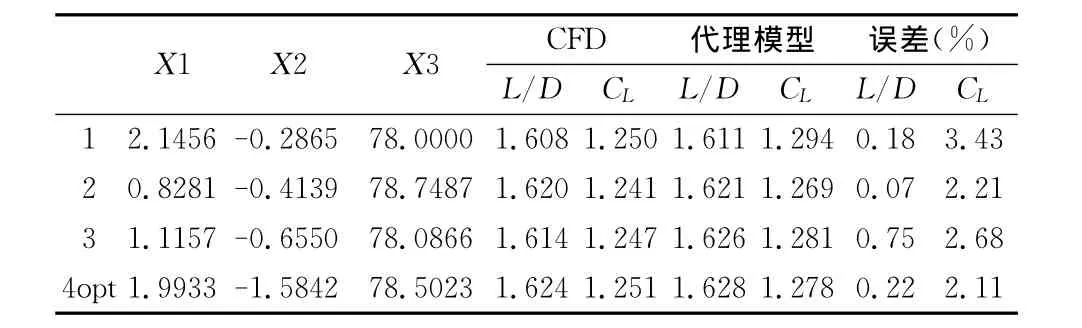
表5 目标函数空间的Pareto解集Table 5 Pareto solution set in objective function space

2.5 试验验证

为验证优化结果的正确性，开展了地面风洞试验对其进行考核，试验模型见图5，试验数据比对见图6和图7。结果对比表明本文采用的优化方法，合理可行，可满足工程设计需求。

图5 风洞试验照片Fig.5 Photo of test in wind tunnel

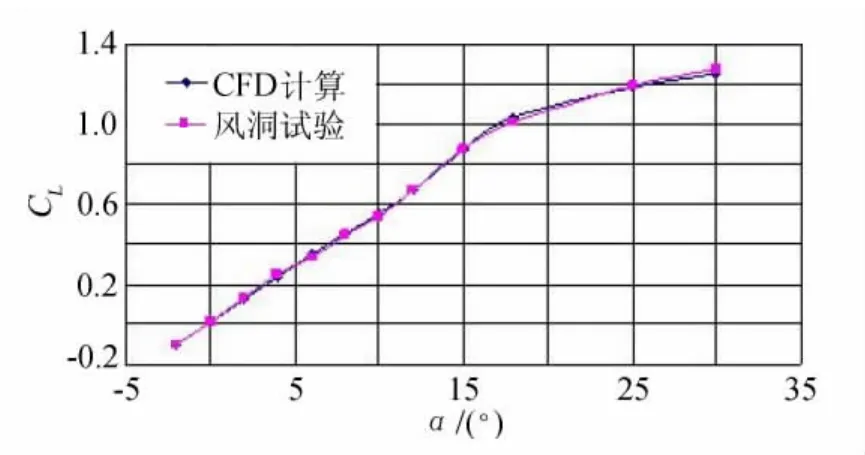
图6 升力系数比较Fig.6 Comparison of lift coefficient

图7 升阻比比较Fig.7 Comparison of lift to drag ratio

3 结 论

本文针对亚轨道可重复使用飞行器（SRLV）气动设计要求高，约束多的特点，优化困难的特点，采用基于Kriging响应面方法的代理模型方法，开展了多约束条件下的亚轨道飞行器的亚声速气动特性优化设计工作，通过数值计算和风洞试验验证了优化结果。结果表明，新方法具有高效、高精度和实用性的优点，能够应用于气动布局的工程设计工作。

［1］熊俊涛，乔志德，杨旭东，等.基于黏性伴随方法的跨声速机翼气动优化设计［J］.航空学报，2007，28（2）：281－285.

［2］何开锋，钱炜祺，陈坚强，等.基于流体力学和电磁学方程数值求解的飞行器气动隐身一体化设计［J］.空气动力学学报，2009，27（2）：180－185.

［3］何开锋，钱炜祺，刘刚，等.飞行器气动隐身一体化设计方法研究［J］.空气动力学学报，2006，24（2）：169－174.

［4］张德虎，高正红，李焦赞，等.代理模型选样准则研究［J］.空气动力学学报，2011，29（6）：719－722.

［5］SIMPSON T W，et al.Kriging models for global approxi－mation in simulation－based multidisciplinary design optimization［J］.AIAA Journal，2001，39（12）：2233－2241.

［6］何开锋，钱炜祺，陈坚强，等.基于流体力学和电磁学方程数值求解的飞行器气动隐身一体化设计［J］.空气动力学报，2009，27（2）：180－185.

［7］叶友达.近空间高速飞行器气动特性研究与布局设计优化［J］.力学进展，2009，06：39（6）：683－694.

［8］PIRONNEAU O.On optimum profiles in stokes flow［J］.J Fluid Mech，1973，59（1）：117－128.

［9］BURGREEN G W，BAYSAL O.Aerodynamic shape optimization using preconditioned conjugate gradient methods［R］.AIAA Paper 93－3322，1993.

［10］BURGREEN G W，BAYSAL O.Three－dimensional aerodynamic shape optimization of wings using using sensitivity analysis［R］.AIAA Paper 94－0094，1994.

［11］FELKER F F.Calculation of optimum airfoils using direct solutions of the N－S equations［R］.AIAA Paper 93－3323－CP，1993.

［12］王振国.飞行器多学科设计优化理论与应用研究［M］.北京：国防工业出版社.2006.