基于正四棱锥形六元声阵列被动定位的研究*

刘泳锐,刘文怡,甄成方

(中北大学电子测试技术国家重点实验室,太原 030051)

作为物联网的重要领域,在无线传感器网络研究中,被动声定位是一种利用声音目标信号来实现定位的无源探测技术,由于其采用被动探测方式,不辐射电磁波,因此具有很强的隐蔽性。被测目标即使利用隐身和干扰的手段来隐蔽自己,但也会有发出大量的噪声,由于声波的主要能量集中在次声频段,因而绕射能力强、衰减慢,声音目标被动探测技术正是利用目标声源的这一特性实现目标的自动检测、识别、定位和跟踪[1-2]。

对于声音无线传感器网络定位系统,声音采集阵列设计是被动声定位中的一项关键技术。声音采集阵列一般可分为线性阵列、平面阵列和立体阵列等[3-4]。线性阵列是对以阵列所在直线为界的半个平面进行定位。四元平面阵列是对整个平面进行目标定位,同时也可对平面阵列的平面为界所划分的半个空间进行定位,但它不能实现对运动目标全空间定位的要求,而且其方位角、俯仰角以及测量距离很大程度上受各阵元位置和有效声速的影响。立体阵列可以对整个空间进行定位,五元阵列虽然可以对全空间定位,但相对于四元平面阵列不能有效的提高定位精度。本文提出了一种六元正四棱锥形数学模型,并进行了误差分析。仿真结果表明,该模型可以对目标声源进行有效定位,并且定位误差小。

1　六元正四棱锥形数学模型的建立

对于六元正四棱锥形声音阵列建立如图1所示的笛卡尔坐标系,其中六个阵元M0、M1、M2、M3、M4、M5的坐标分别为(0,0,0)、(d/2,0,0)、(0,d/2,0)、(-d/2,0,0)、(0,-d/2,0)、(0,0,d/2)。设声音目标S为点声源,坐标为(x,y,z),俯仰角为θ,方位角为φ,S到六个点的距离分别为r0、r1、r2、r3、r4、r5。S到达M0的时间为t0;Mi相对于Mj的时延为τij,即S相对M0到达M1的时延为τ10,所以S到M2、M3、M4、M5的时延为τ20、τ30、τ40、τ50。设声速均匀为c。

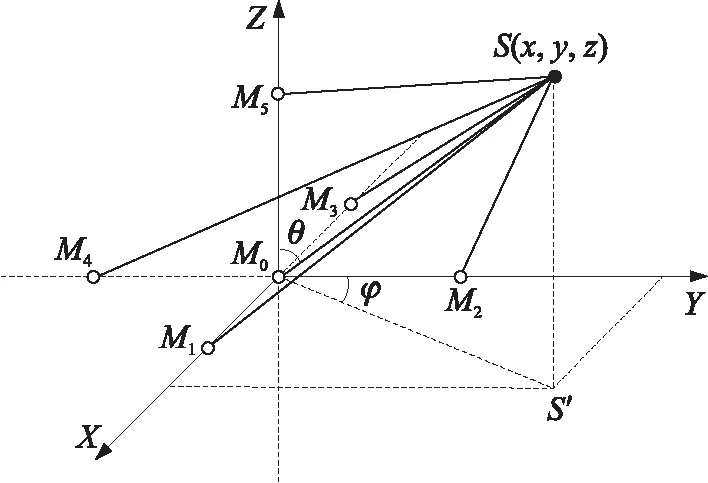
图1　六元正四棱锥形声音阵列原理图

根据相应的几何关系可得:

(1)

(2)

由式(1)得,

(3)

将式(2)代入式(3)得,

(t0+τ10)2+(t0+τ30)2=(t0+τ20)2+(t0+τ40)2

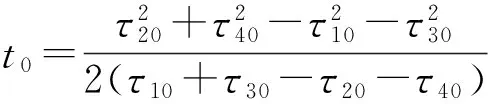
从而由式(1)得,

(4)

其中:r0=ct0,r1=c(t0+τ10),r2=c(t0+τ20),r5=c(t0+τ50)。

由几何关系得,

所以得到球面坐标为:

(5)

其中x、y、t0已由式(5)给出。

由上述可见,通过该模型可以通过测量τ10、τ20、τ30、τ40、τ50,并结合声速c确定目标S的空间位置,完成对声音目标的定位。

2　延时估计

由式(4)和式(5)可知,对声音运动目标的测量依赖于时延,时延估计TDE(Time Delay Estimation)是声音定位领域的一项关键技术,它是指传感器阵列中不同传感器接收到的同源信号之间由于传输距离不同而引起的时间差。基于TDE的声源定位就要先估计出信号在不同阵元处的到达时间差TDOA(Time Delay Of Arrival)[5-6]。一般地,时延估计的算法包括广义相互函数法[7]、互功率谱相位法、自适应滤波法和参量模型法等[8-9]。互功率谱相位法由于目标信号的频率较低、实时性要求高,最小二乘拟合次数不能太高,所以常常用在估计精度不高的场合。自适应滤波法运算速度快,但在点声源的干扰下对其估计精度影响较大。广义互相关法具有较好的综合性能,因此应用较为广泛[10-12]。

利用互相关算法可以非常方便的求出两路信号的时延D从而计算出节点间的距离。设x1(t)、x2(t)分别为两个声传感器接收到的声音信号,S(t)为目标声源信号,D为声阵列中两阵元间的信号传播时延,n1(t)、n2(t)分别为两阵元传感器的加性噪声。并且假设声源信号和噪声信号均符合均值为0、方差为1的正态平稳随机过程,且三者之间互不相关。则x1(t)、x2(t)表示为:

为计算方便,我们假设α=1。

利用广义互相关算法可以得到x1(t)、x2(t)的互相关函数为:

Rx1x2(τ)=E[x1(t)·x2(t+τ)]

(6)

对式(6)展开整理可以得到:

Rx1x2(τ)=E[(s(t)+n1(t))(s(t-D+τ)+n2(t+τ))]

=E[s(t)·s(t-D+τ)]=RSS(τ-D)

由上式可知,当x1(t)、x2(t)互相关函数取得最大值时,RSS(τ-D)也同时取得最大值,又因为RSS(τ-D)≤RSS(0),所以取得最大值的时候τ=D,即求出τ就可以得到时延D。

对于时延D,需要对信号x1(t)和x2(t)进行预处理,然后再送入相关器求互相关函数,这种方法称之为广义互相关法。

广义互相关时延估计方法模型是由滤波器H、乘法器、积分器、平方器和峰值检测器组成。如图2所示。

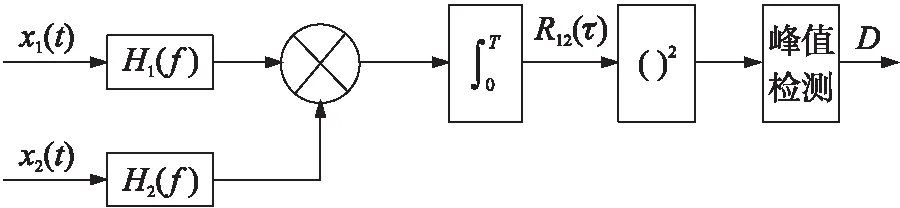
图2　广义互相关时延估计方法模型

信号x1(t)和x2(t)经过加窗滤波后,得到互功率谱函数:

由于互相关函数与互功率谱函数之间是一对傅立叶变换的关系,因此相关函数为:

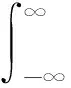
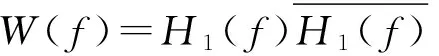
由上式可知,当权函数W(f)=1时,即为一般的互相关法。

3　误差分析

3.1　方位角、俯仰角误差分析

3.1.1俯仰角误差分析

通过式(1)和式(2)得到:

(7)

由于时延的统计误差特性相同,故假设时延估计的标准差为:δτ10=δτ20=δτ30=δτ40=δτ50=δτ且相互独立。

因此俯仰角误差估计为:

(8)

对式(7)中θ分别求偏导数得:

(9)

将式(9)代入式(8)得到:

(10)

由式(7)和式(10)变形化简得到:

(11)

由式(11)可知:俯仰角估计的精度受时延估计误差、声音传感器阵列的尺寸和声源俯仰角的影响。

3.1.2方位角误差分析

方位角误差估计为:

(12)

对式(7)中φ分别求偏导数得:

(13)

将式(13)代入式(12)得到:

(14)

由式(7)和式(14)变形化简得到:

(15)

由式(15)可知:方位角估计的精度受时延估计误差、声音传感器阵列的尺寸和声源俯仰角的影响。

3.2　距离误差分析

由式(1)和式(2)得到如下表达式:

(16)

距离误差估计为:

(17)

通过计算得到时延τi0为:

(18)

用泰勒公式展开,同时忽略高阶无穷小,可以得到:

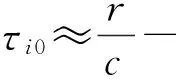
(19)

化简得:

(20)

对式(20)两边同时求和得:

(21)

代入下式:

(22)

可以得出:

(23)

因为

(24)

上式两边分别对τi0(i=1,2,3,4)求偏导数并化简得:

(25)

将式(23)代入式(25)可得

(26)

将式(26)代入式(17)得到:

(27)

由式(27)可知:距离误差估计的精度受时延估计精度、声音传感器阵列的尺寸和声源俯仰角的影响,与方位角没有关系。

4　实验结果

为验证模型设计的正确性,使用MATLAB R2010a软件编写算法,进行仿真计算。仿真声源的位置为S1(50,40,60),S2(-120,80,70),表1为使用MATLAB求出的数学模型理论值与模型误差。实际使用时将正四棱锥的底面贴近地平面安装,就可以对地平面上方的全空间进行定位。如果需要对地下目标进行定位,可以将正四棱锥底面安装在高处,将阵元M5点安放在下方即可。

表1　数学模型理论值与模型误差

5　结论

文中提出了一种正四棱锥形六元声音被动定位模型。在理论上进行了推导,并给出了计算公式。最后使用MATLAB软件进行模型仿真计算,给出了理论值和模型误差。

参考文献:

[1]王巍,薛安克,林岳松等.无源单传感器声目标纯方位定位改进算法[J].杭州电子科技大学学报,2005,25(3):71-73.

[2]周红波,邢昌风,耿伯英等.无线传感器网络分布式多目标跟踪算法研究[J].传感技术学报,2011,24(2):287-293.

[3]吴晓,靳世久,李一博等.基于麦克风阵列声音信号定位方法的研究[J].传感技术学报,2010,23(5):682-688.

[4]陈华伟,赵俊渭,蔡宗义等.两种声学阵列的定向精度分析与仿真[J].声学与电子工程,2001,(3):6-11.

[5]程萍,陈建峰,马驰等.十字阵短时段宽带声源实时定向算法[J].应用声学.2012,31(2):123-129.

[6]叶摇永,陈建峰,程摇萍等.用于麦克风阵列的阵元筛选方法研究[J].传感技术学报,2012,25(11):1507-1510.

[7]Ruiy,Florencio D.Time delay estimation in the presence of correlated noise and reverberation[J].IEEE International Conference on Acoustics,Speech,and Signal Processing,2004,2(2):133-136.

[8]韩霜,罗海勇,陈颖等.基于TDOA的超声波室内定位系统的设计与实现[J].传感技术学报,2010,23(3):347-353.

[9]崔玮玮,曹志刚,魏建强.声源定位中的时延估计技术[J].数据采集与处理,2007,22(1):90-99.

[10]孙韶杰,孙绍俊,李国辉等.一种改进的声测定位时延估计算法[J].计算机应用,2006,26(11):2696-2697,2723.

[11]徐耀松,付摇华,王丹丹,基于广义加权的AMDF 时延估计方法研究[J],传感技术学报,2013,26(3):421-424.

[12]林晓东,吴松林,张川.六元探测基阵被动声定位算法及其性能研究[J].声学技术,2008,27(2):192-196.

刘泳锐(1988-),男,现为中北大学在读硕士研究生,研究方向为测试计量技术及仪器,lyr403@163.com;

刘文怡(1970-),男,现为中北大学博士生导师,研究方向为航天智能测量系统。