基于BIC准则模型选择的光纤光栅波长温度拟合研究*

贾桂文,张景川,陈德旺*,王丽娟

(1.北京交通大学轨道交通控制与安全国家重点实验室,北京 100044;2.北京卫星环境工程研究所,北京 100094)

光纤光栅因其易于光纤连接、低损耗、光谱特性好、可靠性高等特点,以及其制作技术的不断成熟和应用研究的不断深入,近年来得到广泛关注。同时,作为传感元件,它有其他传感器无可比拟的优点,即感应的信息采用波长编码,而波长这一参量不受光源功率的波动和连接损耗或耦合损耗的影响。国内外从事光纤光栅相关研究的学者,分别在光纤光栅的理论、形成机理、写入技术、封装结构、不同物理量传感器设计、传感网络调制解调及工程应用等方面做了大量研究[1-2]。

外界温度的改变使得光纤光栅中心波长发生漂移,即温度的变化量会体现在波长的变化上,当材料确定后,光纤光栅对温度的灵敏度系数是与材料系数相关的常数,这就从理论上保证了以光纤光栅作为温度传感器可以得到很好地线性输出。正是这一特性,近几年,光纤光栅在工程测温上得到广泛应用。

本文研究的重点是传感网络的温度解调部分。对此,聂俊提出根据光纤布里渊频移和温度、应变之间的关系,确定光纤各小区段上能量转移达到最大时的频率差,进而得到温度和应变的信息,实现分布式测量的探讨,但其测量结构比较复杂的物体时,需要布置更多的光纤传感器[3]。此外,常用的解调方法还有匹配光纤光栅可调滤波检测法[4]、非平衡M-Z干涉仪法[5]、可调光纤F-P滤波检测法[6]、可调窄带光源检测法[7]等,上述这些解调方法大多基于硬件解调。同时,还有相关学者尝试从解调算法上进行研究,如2006年比利时C.Caucheteur等提出将Nelder-Mead单纯形算法引入到对保偏光纤光栅传感器的检测中[8],该算法比较简单,但收敛速度较慢,适合变元数不是很多的方程求极值,丁晖将粒子群优化算法应用到光纤光栅传感器波长解调中[9]。以上硬件方法灵活性比较差,而提出的几种解调算法,不易实现,实时性不好,同时,现有研究多针对波长解调[10-11],为此,基于温度解调,本文提出将多项式拟合与BIC模型选择应用到光纤光栅解调系统。

1　数据采集与分析

我们从现场光纤光栅解调系统的历史数据中获取波长和温度信息,分别为{λ(1),λ(2),…,λ(n)},{T(1),T(2),…,T(n)},共6 766组数据,其中,温度数据为标定值。数据分布如图1,从图中可以看出,波长和温度近似服从线性分布,进而我们采用多项式拟合的方法逼近光纤光栅波长温度曲线。

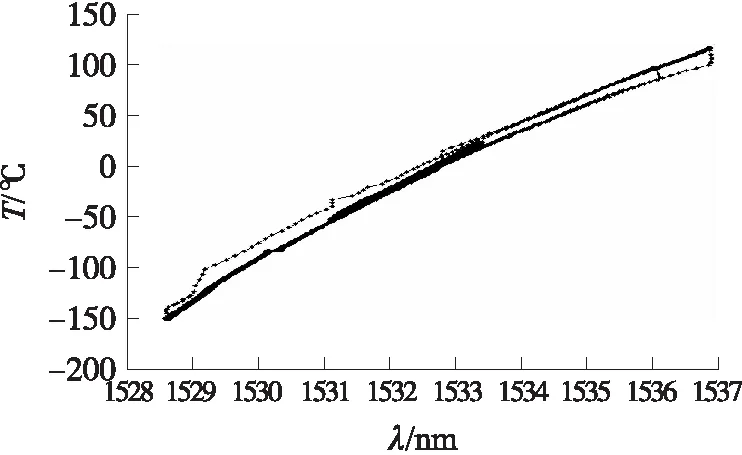
图1　波长和温度原始数据

2　算法原理

2.1　多项式拟合

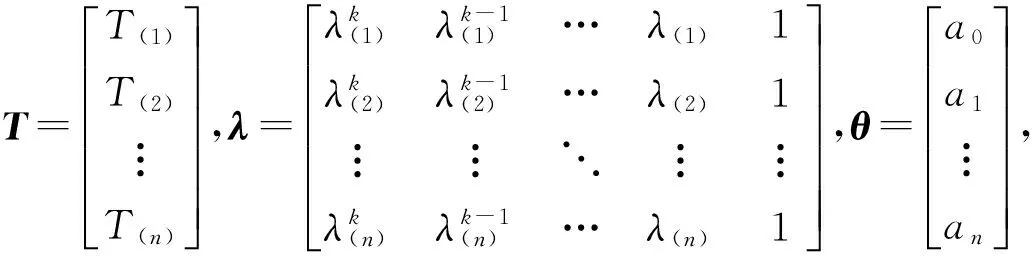
假设拟合得到的多项式为

(1)

2.2　AIC信息准则

1971年,日本统计学家H.Akaike在研究信息论特别是在解决时间序列定阶问题中提出了赤池信息准则(Akaike’s Information Criterion,AIC)[12]。其定义如下,

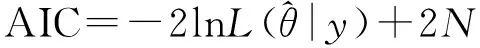
(2)

2.3　BIC准则

但是本文讨论的问题是大样本情况,AIC信息准则有其缺陷。当样本很大时,AIC信息准则中左一项很大,使得模型参数个数对AIC的贡献很小,进而对于大样本情况,AIC失效。为此,Schwarz提出BIC准则[13-14],其公式如下,

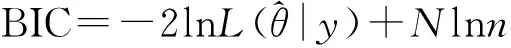
(3)

BIC=nln(Re/n)+Nlnn

(4)

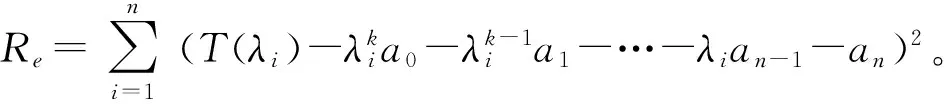
3　计算结果与分析

多项式拟合时,阶数越高,参数越多,均方根误差越小,通常我们会选择均方根误差较小的模型,然而,这里存在过拟合现象。均方根误差定义如下,

(5)

图2　均方根误差曲线

我们得到1到20阶的均方根误差曲线,如图2所示。从图2可以看出,随着阶次的增大,均方根误差的值在逐渐减小。从图3可以看出当阶次为6时,BIC的值最小为BICmin=9.182×103,此时AIC也取得最小值,ERMS(6)=1.962 0,只是AIC准则在阶次大于6时变化不明显,这是因为阶次大于6时模型参数的个数对AIC的贡献不大。可见,并不是均方根误差越小,模型越好。通过计算BIC,我们得到,当阶次为6时,BIC最小,即此时模型在误差和模型参数的要求达到最佳,模型最好。

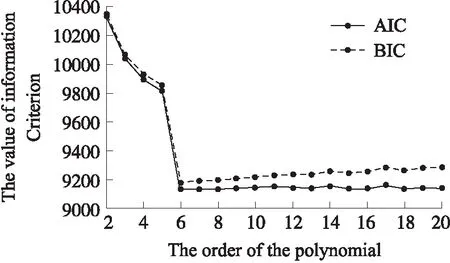
图3　阶次与模型评价准则的关系

为评价六阶多项式模型和原解调系统的解调精度,我们定义绝对平均误差ACE如下,

(6)

其中,ei同式(5),六阶多项式模型和原解调系统的误差分析如表1所示。

表1　六阶多项式与原解调系统比较

从表1中可以看出,六阶多项式模型比原解调系统的ERMS和ACE分别提高16.5%和22.9%。同时,六阶多项式模型的运行时间为0.235 s,具有较好的实时性。

当多项式阶次为6时,模型参数个数为7,分别为a0=5.788×10-6,a1=-0.035 79,a2=70.285,a3=-7 039.463,a4=-1.489×108,a5=1.876×1011,a6=-7.251×1013,得到的多项式拟合曲线如图4所示。尽管当阶次为19时,均方根误差取得最小值,此时的均方根误差值为,ERMS(19)=1.958 3,但由BIC准

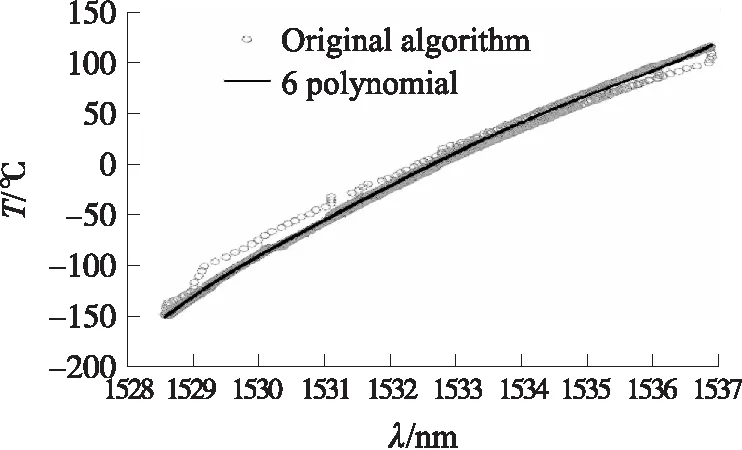
图4　六阶多项式拟合曲线

则可知,当阶次为19时,虽然模型误差较小,但模型参数过多,并不是最佳模型。

5　结论

本文提出将BIC模型选择准则和多项式拟合应用于光纤光栅温度解调中,得到阶次为6时BIC值最小,而此时的均方根误差值也适中,满足现场温控系统中温度监测的系统测试要求。该方法具有实时性好,便于工程实现等特点,其同样适用于应变解调及其他光纤光栅传感器,此时的均方根误差同时为后续研究提供参考。

参考文献:

[1]龚剑,刘颖浩,袁勇.大面积高强混凝土早期温度、应变测试与分析[J].结构工程师,2012,28(1):111-116.

[2]余乐文,张达,余斌,等.基于FBG的矿山安全监测传感器特性研究[J].矿冶,2011,20(4):5-8.

[3]聂俊,李瑞有,梁俊.基于BOTDA的温度和应变测试探讨[J].长江科学院院报,2011,28(4):67-70.

[4]刘云启,刘志国,郭转运,等.光纤光栅传感器的调谐滤波检测技术[J].光学学报,2001,21(1):88-92.

[5]Weis R S,Kersey A D,Berkoff T A.A Four-Element Fiber Grating Sensor Array with Phase-Sensitive Detection[J].IEEE Photonics Technology Lett,1994,6(12):1469-1472.

[6]余有龙,潭华耀,锤永康.基于可调F-P滤波器的光纤光栅传感器阵列查询技术[J].中国激光,2000,27(12):1103-1106.

[7]张昕明,余有龙,朱勇.光纤光栅传感系统信号解调技术[J].光电子技术与信息,2002,15(4):17-20.

[8]Caucheteur C,Lhomme F,Chah K,et al.Simutaneous Strain and Temperature Sensor Based on the Numerical Reconstruction of Polarization Maintaining Fiber Bragg Gratings[J].Opt Laser in Eng,2006,44:411-422.

[9]丁晖,吴相楠,梁建奇,等.粒子群优化算法在光纤光栅传感器波长解调中的应用[J].光谱学与光谱分析,2010,30(2):563-566.

[10]丁锋,王粉艳,王云建,等.一种光纤光栅振动与温度同时区分测量的解调方法[J].传感技术学报,2012,25(4):510-514.

[11]李立新,吴飞,蔡璐璐,等.利用扭转高双折射光纤实现波长解调的方法[J].传感技术学报,2006,19(4):1212-1214,1218.

[12]秦宣云.基于AIC准则的最近邻聚类模型的优化算法[J].系统工程与电子技术,2005,27(2):257-259.

[13]郑元兵,陈伟根,李剑,等.基于BIC与SVRM的变压器油中气体预测模型[J].电力自动化设备,2011,31(9):46-49.

[14]刘伟峰,杨爱兰.基于BIC准则和Gibbs采样的有限混合模型无监督学习算法[J].电子学报,2011,29(03):134-139.

贾桂文(1987-)男,北京交通大学控制工程专业研究生,研究方向为光纤传感技术,10125057@bjtu.edu.cn;

陈德旺(1976-)男,北京交通大学电子信息工程学院教授,博士生导师,主要研究领域为交通信息工程与控制;软计算、智能计算、最优化、机器学习在交通系统中的应用,光纤传感技术等,dwchen@bjtu.edu.cn。