基于分数阶小波变换的心电信号去噪处理研究

尚 宇，刘素勤

（西安工业大学 电子信息工程学院，西安710021）

心电信号（Electrocardiosignal，ECG）是非平稳的微弱信号，经常会受到噪声的污染而影响临床诊断和分析的准确度，为了给医生提供清晰的心电图型，以提高分析和诊断的精确度，就必须对ECG进行一定的分析处理，使其数据曲线平滑，特征点突出.目前，国内外有很多学者对它进行研究，有的用经典的小波变换（Wavelet Transform，WT），有的用傅里叶变换，有的用低通滤波器，这些方法对心电信号的去噪计算量小，速度快；但是他们都仅局限于在全局分析，有时会忽略信号的细节、突变等部分细小的重要成分，造成重构后信号部分位移等出现，给医生诊断病人心电图带来不便.而分数阶 傅 里 叶 变 换 （Fractional Fourier Transform，FRFT）主要对信号进行局部分析.本文采用分数阶小波变换（Fractional Wavelet Transform，FRWT）将FRFT变换和WT变换相结合，利用 WT变换中的多分辨分析理论和FRFT的时频聚焦性相结合对含噪的ECG进行去噪，克服了单一变换的不足，从而保证时域分辨率的一致性和有效性.实验表明，该方法能够得到很好的处理效果.

1 心电信号

ECG信号的幅度在10μv～4μv，一般正常的心电信号频率为0.01～100Hz，90%的频率能量集中在0.25～40Hz之间，ECG从0.05Hz处开始有一个峰值，在1.1Hz附近处出现最大峰值，以后峰值的总体趋势逐渐下降，到35Hz处峰值下降为0.05Hz处峰值的1／26，下降到最大峰值处的1／33.故可认为ECG信号频率主要分布在0.25～40Hz［1］.在采集、放大及传输ECG信号的过程中，由于受人体、采集仪器、电磁环境、操作水平等的影响，不可避免会有许多干扰耦合到ECG信号.因此采集的信号主要干扰有：①由于电磁场作用于心电图的导联与人体之间的环形电路所致的50Hz的工频干扰，表现为ECG信号上有明显的正弦波或正弦波的叠加信号；②由于人体活动，肌肉紧张所引起的肌电干扰，表现为不规则的快速变化波形，幅度为毫伏级；③由于人体呼吸运动、电极接触不良等因素所导致的基线漂移，表现为心电信号上叠加缓慢变化的信号.

2 小波变换

在信号分析过程中，为了使时频分辨率能够根据信号的特点自动地调节，J.Morlet于1984年提出了WT变换，德尔概念，并将其用于分析地震波的局部特征.信号f（t）∈L2（R）的 WT 变换［2］定义为

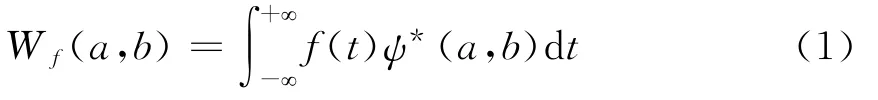
其中，a∈R＋和b∈R分别表示尺度因子和识别因子，且小波基函数ψa，b（t）为

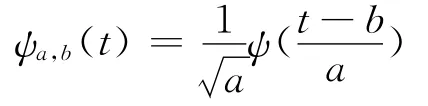
其中，ψ（t）称为母小波函数.先对式（1）右边变量b作傅里叶变换，然后再作傅里叶变换的逆变换，可得WT变换的频域表达形式为

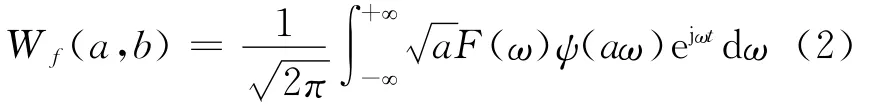
WT变换不但有时间和频率的定位功能，且有自动调节时间和频率分辨率的能力.由于 WT变换只局限在时频域内分析信号，由式（2）可看出WT变换可看成是一组频域带通滤波器组.

ECG信号滤波的首要问题是小波基函数的选取.采用不同的小波基函数对同一个信号，会得到不同结果，但是小波基的选取要遵守以下原则：①正交性，可以使分析简单，有利于信号的精确重构；②对称性，对称性的小波基函数使得小波滤波呈现线性相位，信号不会失真；③紧支性，紧支集长度决定着信号局部特征的好坏，紧支集越短的小波函数局部时频特性就越好；④正则性，正则性决定着信号的重构效果，继而影响频域的分辨率.以下是对MIT-BIH中的含噪信号进行WT变换处理，对含噪信号采用db1小波函数进行阈值处理，计算输入信噪比为－6.131 9dB，去噪后信噪比达到6.252 8dB，如图1所示含噪信号和去噪后的信号及如图2所示两个信号的对比可看到，对于频域能量聚集的信号，WT变换就能够取得最优结果，而对于那些频域能量非聚集的信号，其结果将不是最优的.

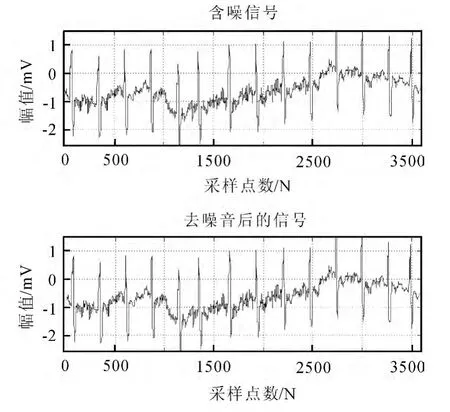
图1 含噪信号和去噪后的信号Fig.1 Noisy signal and denoised signal

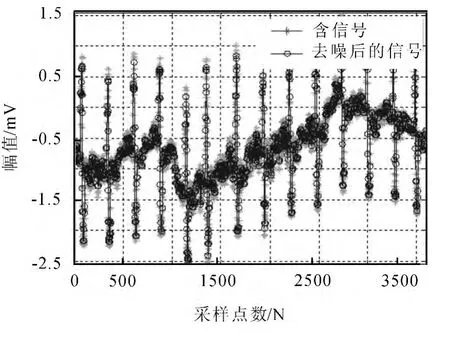
图2 信号去噪前后的对比Fig.2 Comprison between the singals before and after being denoised

3 分数阶小波变换

FRWT变换的概念最早出现于1997年，目前FRWT变换理论的定义主要有以下三种类型［3］.

1）将WT变换和FRFT变换相结合形成的FRWT换.早在1997年，Mendlovic和Zalevsky就首次给出了FRWT变换的定义、分解形式和重构公式［4］，1998年 Huang Ying给出了分数阶小波包变（Fractimal Warelet Packet Transform，FRWPT）的定义并证明了该变换满足能量守恒定律［5］，这两种定义是FRFT变换和WT变换发展起来的，都是全新的定义形式.

2）通过寻找分数阶函数构造小波基形成的FRWT变换.这种FRWT变换的定义与第一种完全不同.他是通过构造分数阶小波基函数来获得，最为常见的就是样条 WT变换，文献［6-8］研究了分数B样条小波，给出了具体的表达式，并推导出了基于离散Fourier变换的分数B样条小波分解和重构公式，为FRWT变换研究奠定了基础，例如，文献［9］定义的正交分数阶样条小波滤波器，使用快速Fourier算法，对于这种分数阶样条小波滤波器快速Fourier算法实现速度较快.

3）WT变换和FRFT变换相融合的方法.文献［9］扩展了文献［10］的研究，将正交小波和多分辨率分析引入FRFT变换的核函数，用L2（R）的其他正交基来代替Hermite–Gaussian函数，新的正交基间接从多分辨分析和正交的小波中获得.

针对心电信号属于非平稳信号，文中采用第一种定义.利用FRWT对含噪心电信号进行去噪处理，为了得到精确的最佳变换域采用二重搜索［11］的方法，其主要步骤是：首先对信号进行Fourier变换，在（α，μ）平面上进行峰值点的二维搜索，得到α0，μ0的粗略估计值，然后以这估计值为初始值，利用拟Newtou法进行迭代搜索，得到参数的精确估计，其迭代过程为

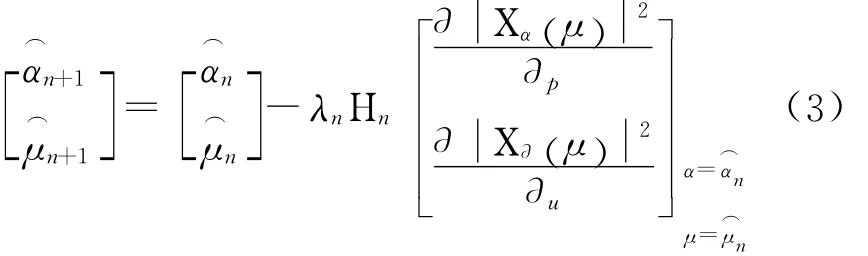
文中基于FRWT变换的思想是即先对信号进行FRWT变换，在此基础上采用二维搜索和拟牛顿法相结合的方式搜索最佳变换阶数p，然后对信号进行p阶FRFT变换，再对变换后的信后进行WT变换处理，最后进行－p阶的FRFT变换.具体流程图如图3所示.

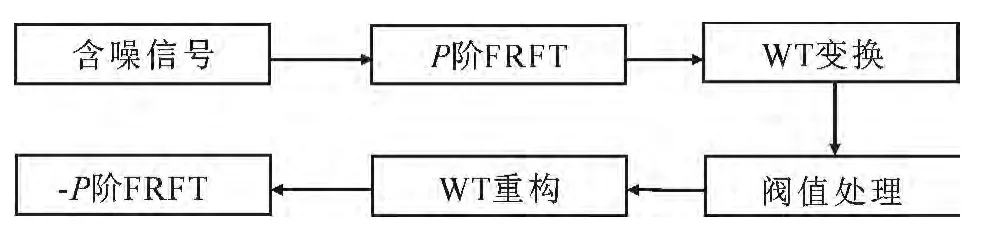
图3 FRWT去噪过程Fig.3 Denoising process

可概括FRWT变换对ECG信号去噪的步骤为

1）将含噪信号输入，由于0～2阶和2～4是对称的，因此只需求输入信号的0～2阶的FRFT.

2）在0～2阶域FRFT变换中运用二维搜索和拟牛顿法相结合迭代搜索最佳变换阶数p.

3）做信号最优p阶FRFT变换.

4）在p阶域FRFT内对信号做WT变换.

5）对变换后的信号做－p阶FRFT变换得到时域输出信号.

4 仿真实验

4.1 心电信号读入Mmatlab

文中所用的仿真心电数据来自MIT－BIH中的 “Arrhythmia Database”和 “Noise stress Test Database数据库.该数据库中的数据采样率为360 Hz，数模转换（Analog－to－Didital Conventer，ADC）分辨率为11位，记录时间为0：00：000～30：05：556，按采样率来计算得出采样点数为649 080个点，由此可知，采样点数非常庞大，在实际处理时，只需采用其中具有代表性的部分点数作为研究对象，现以“Arrhythmia Database”数据库中第118号心电数据为例，ECG信号的周期约为1s.为了能够切实地分析问题，又不会增加计算量，现选取粘脂贮积病II（Mucolipidosis II，MLII）导联方式下的信号，存储格式为212，截取3 600个点进行仿真分析.

4.2 仿真实验

在该实验中，首先将信号读入到Matlab中，计算输入信号的信噪比为－6.131 7dB.对含噪信号做FRFT，在（α，u）平面上进行二维搜索，得到α0＝45.045 3，μ0＝1 801的粗略估计值，然后以这估计值为初始值，利用拟Newtou法中进行搜索步长为0.001，迭代次数为100次的搜索，得到最佳变换阶数p＝1.01.在此阶数上对含噪信号进行FRFT，在FRFT域内对变换的信号进行db1小波去噪，对滤波后的信号进行－1.01阶的FRFT，仿真结果如图4所示.

对“Noise stress Test Databases”数 据 库 中118，119号信号进行测试，仿真结果见表1.

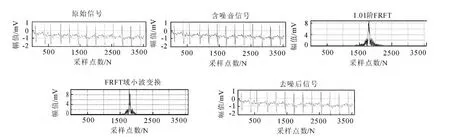
图4 FRWT变换Fig.4 Fractional wavelet transform

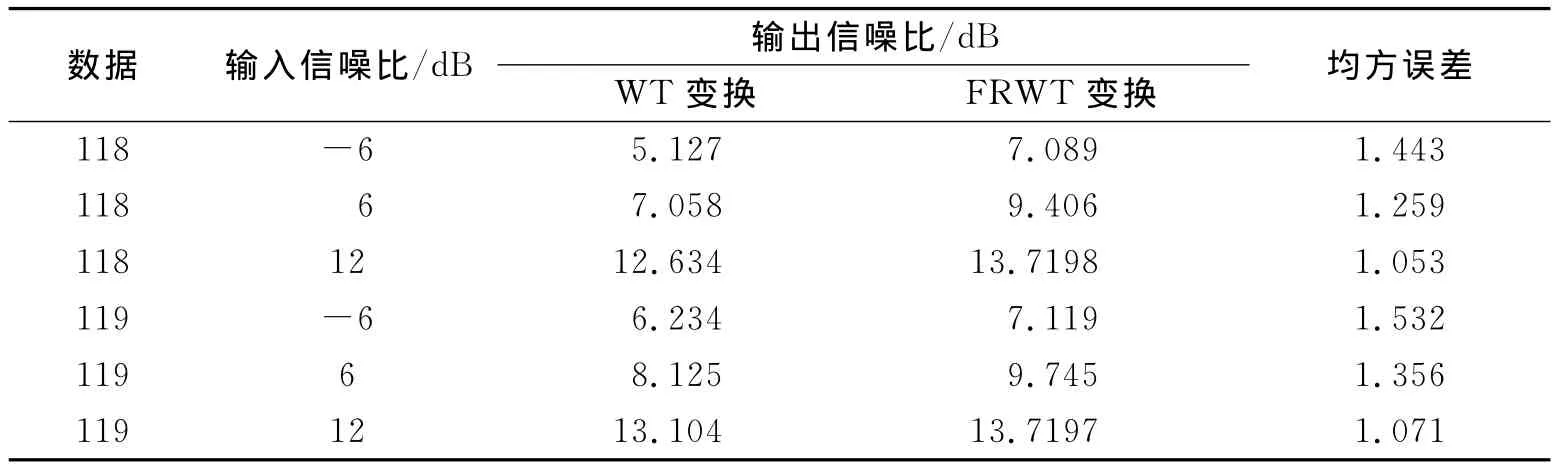
表1 不同输入信噪比下的滤波效果Tab.1 Filtering effects of different input SNR

5 结 论

文中通过对ECG信号特点的研究以及现有的一些方法讨论，在FTFT变换和WT变换的基础上，运用FRWT变换，对ECG信号进行去噪处理，通过试验，可以看出，在搜索到的最佳变换域内，运用FRWT变换比运用WT变换对ECG信号去噪上的效果更好，运用FRWT变换对ECG信号处理，计算量少，算法简单，具有很广泛的使用价值.

［1］ 尚宇，徐婷.分数阶Fourier在心电信号处理中的应用研究［J］.西安工业大学学报，2012，32（10）：857.SHANG Yu，XU Ting.The applications Research of the Fractional Fourier Transform in the ECG Processing［J］.Journal of Xi’an Technological University，2012，32（10）：857.（in Chinese）

［2］ MALLAT S.A Wavelet Tour of Signal Processing：the Sparse Way，3rd Edition，Boca Raton［M］.Acadomic Press：CRC Press，2008.

［3］ 路倩倩，王友仁，罗 慧.二维分数阶小波变换滤除混合图像噪声研究［J］.佳木斯大学学报，2012，30（02）：218.LU Qian-qian，WANG You－ren，LUO Hui.Mixed Image Noise Study Two －dimensional Fractional Wavelet Transform Filter［J］.Journal of Jiamusi University，2012，30（02）：218.（in Chinese）

［4］ MENDLOVIC D，ZZLEVSKY Z，MAS D，et al.Fractional Wavelet Transform［J］.Applied Optics，1997，36（20）：4801.

［5］ HUANG Y.The Fractional Wave Packet Transform［J］.Multidimensional Systems and Signal Processing，1998，4（9）：399.

［6］ UNSER M，BLU T.Construction of Fractional Spline Wavelet Bases［M］.Bellingham：SPIE-INT SocOptical Engineering，1999.

［7］ UNSER M，BLU T.Fractional Splines and Wavelets［J］.SIAM Review，2000，42（1）：43.

［8］ LUT T，UNSER M.The Fractional Spline Wavelet Transform：Definition end Implementation［C］／／IEEE International Conference on Acoustics，Speech，and Signal Processing，Istanbul，Turkey，2000，6：512.

［9］ YUAN L.Wavelet－fractional Fourier transforms［J］.Institute of Physics Publishing，2008，17（1）：170.

［10］ ALPANA B，NAVEEN K，NISHCAHI A，et al.Extended Fractional Vavelet Joint Transform Correlator［J］.Optics Communications，2008，281（1）：44.

［11］ 齐林，陶然，周思永，等.基于分数阶Fourier变换的多分量LMF信号的检测和参数估计［J］，中国科学，2003，33（8）：749.QI Lin，TAO Ran，ZHOU Si－yong，et al.Detection and Parameter Estimation Based on Fractional Fourier Transform of the Multi－component Signals LMF［J］.Science in China，2003，33（8）：749.（in Chinese）