重复观测生存数据的AR(1)随机效应建模和估计*

王宁宁 徐淑一 方积乾

在生物科学中，经常遇到同一个体的多次观测，比如同一个病人手术后疾病经常反复发作，一个文献中经常被引用并研究的数据是慢性肉芽肿病(chronic granulomatous disease，CGD)数据。Yau和McGILCHRIST (1998)[1]对这种数据建立AR(1)结构的Frailty模型，进行了ML估计和REML估计，他们的估计相当于利用调整的集中化扩展似然函数分别对方差和相关系数进行估计，没有考虑二者的联合信息。

由Lee和Nelder(1996)[2]提出的带随机效应的广义线性模型的等级似然(hierarchicacl likelihood)估计方法，允许随机效应因子是任何分布，等级似然方法近年来开始应用于生存数据的混合模型估计，展现了良好的应用前景。LI.DO.HA等(2001)[3]将等级似然估计方法用于脆弱模型的估计，估计了随机效应(脆弱性因子)呈正态分布和γ分布的情形，并证明了在给定随机效应分布参数的情况下，最大化边际似然得到的协变量系数估计和最大化等级似然得到的协变量系数估计是一致的。LI.DO.HA等(2002)[4]将等级似然估计应用于存在删失数据的混合线性模型，假设随机效应呈正态分布。LI.DO.HA等(2005)[5]将其应用于多重混合线性模型的估计。王宁宁等(2009)[6]将其应用于脆弱性模型的检验。徐淑一和王宁宁(2007，2009，2011)[7-10]将其应用于竞争风险模型的估计与应用研究中。王宁宁等(2011)[11]使用这种方法对威布尔形式的脆弱性模型进行估计和应用。近年来，文献上关于等级似然估计方法在生存分析数据中的研究逐渐增多，基于篇幅，不再一一列举。

本文针对个体重复观测的生存数据，采用AR(1)形式的frailty结构，建立比例危险模型。本文采用等级似然估计方法估计协变量参数并预测随机效应的实现值，采用MAPHL方法估计随机效应分布的参数，并且将ML、REML方法和MAPHL方法比较，并证实了REML估计等价于调整的轮廓等级似然关于θ和ψ的一阶导数等于零的迭代公式。

模型设计和参数估计过程

假设在给定的可观测的协变量X以及不可观测的异质性因子U的条件下，建立比例危险模型如下：λ(t|u)=λ0(t)exp(Xβ)u,记v=log(u)，考虑有q个病人(q个组)，第i个病人重复观测次数为ni，则第i个病人的第j次生存时间的危险率模型为：

λ(tij|u)=λ0(tij)exp(ηij)

(1)

(2)

其中，

(3)

在给定(X,V)条件下，Tij的条件生存函数是：

S(t|X,V)=exp(-Λ(s)exp(ηij))

(4)

那么Tij的条件密度是：

f(t|X,V)=h(s|X,V)exp(-Λ(s)exp(ηij))

(5)

于是，等级似然函数可以写成：

(6)

l1ij=δij{logλ0(yij)+ηij}-{Λ0(yij)exp(ηij)}

(7)

(8)

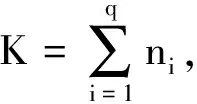
(9)

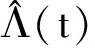
(10)

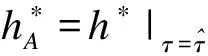
下面详细讨论模型参数的估计步骤。我们设第i组的随机效应的方差阵为：

(11)

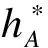
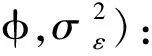
(12)

重复这一步直到收敛。

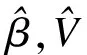
(13)

重复这一步直到收敛。其中，

(14)

随机效应分布参数的MAPHL估计与REML以及ML估计的比较

Yau和McGILCHRIST (1998)推导了随机效应分布参数的REML估计和ML估计。我们采用Lee 和Nelder(1996)的MAPHL估计方法，和REML及ML方法比较，经过推导，得到以下结论：

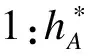
证明：

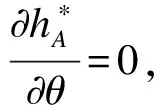
(15)

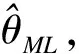
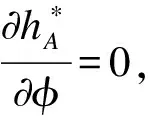
证明：

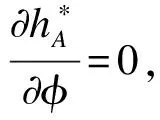
(16)

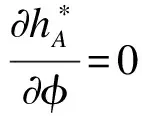
(17)

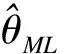
上述REML或者ML估计都相当于调整的等级似然对θ与φ单独求导令其为零得到，这么做显然没有考虑θ与φ的联合信息，因此我们认为联合估计θ与φ更加合理。本文采用SAS的IML语言分别编写了MAPHAL估计和REML以及ML估计的程序，完整的实现了前述估计过程。

应用实例

这一部分对本文开始提到的CGD数据做应用研究，总共128个病人，来自14个不同的医疗机构，主要考察γ干扰素对慢性肉芽肿病的治疗效果，一部分病人采取了γ干扰素措施，其余的病人采用安慰剂作对比。变量rIFN-g=0表示安慰剂，rIFN-g=1表示采用该疗法。为了充分考虑患者个体的不同状况以及尽量控制其他因素的影响，模型还包括了病人身体特征的协变量：病人进入研究时的年龄(Age)、性别(Sex)、身高(Height)以及体重(Weight)；病人的遗传模式(Pattern of Inheritance)，用Inheritance表示；病人在进入研究时是否使用皮质类固醇(Corticosteroids)；病人在进入研究时是否采用了预防性的抗生素(prophylactic antibiotics)。除此之外，模型还考虑了不同的医疗中心的因素，将14个医疗中心分为两类，一类来自于美国，一类来自于欧洲的医疗中心，用Institution category表示。由于很多病人都有重复观测，多的达到7次，需要考虑个体的异质性影响，我们估计九个协变量的AR(1)结构的随机效应模型，结果列在表1中(括号内表示估计的标准差)。

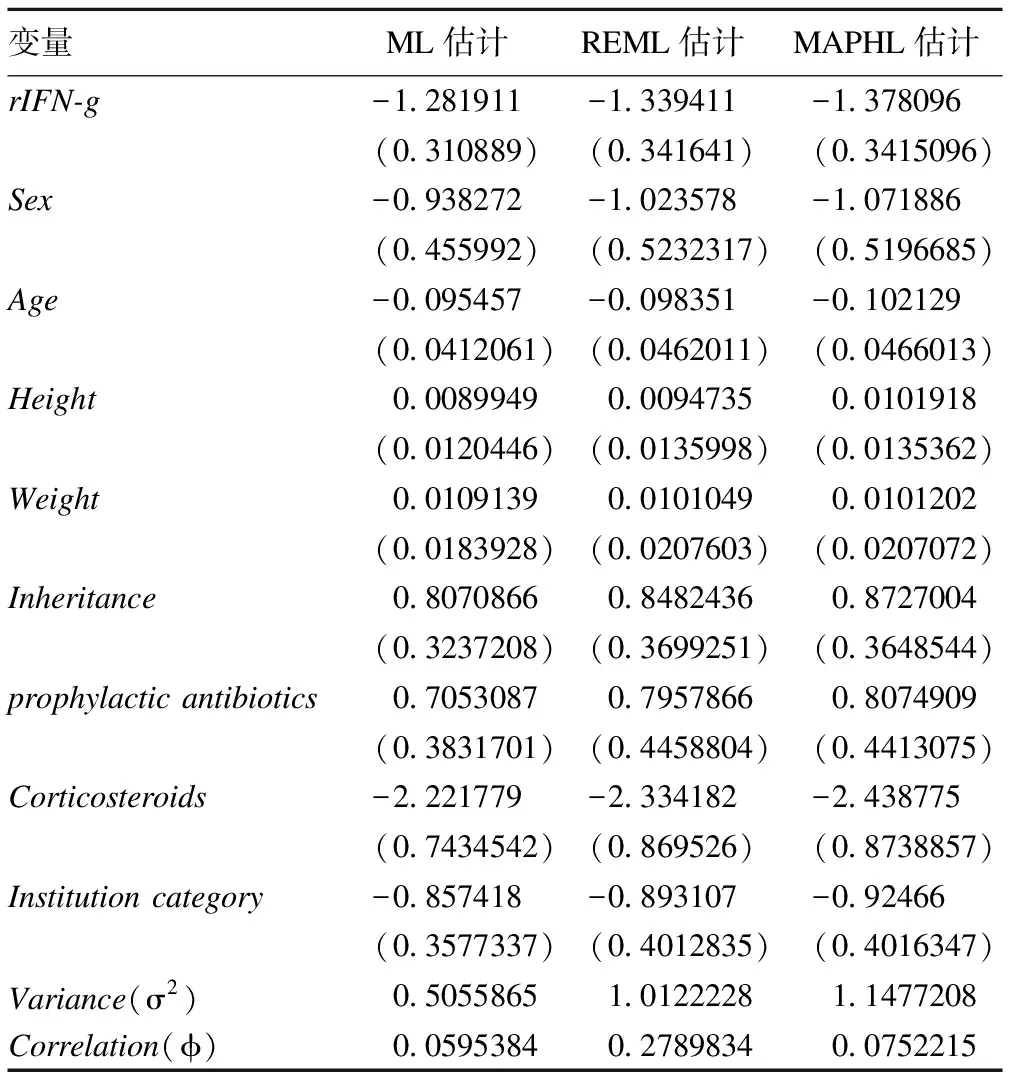
表1 CGD数据的AR(1)随机效应模型的估计结果

我们发现各种估计方法的结果是接近的，而且，协变量参数REML估计和MAPHL估计结果很接近，总的说来，三种方法差别不大，各个变量的显著性很接近。随机效应因子方差的REML和MAPHL估计结果很接近,然而φ的ML和MAPHL估计比较接近，而且非常小，接近于零。不同病人的异质性影响我们认为是存在的，但是φ的估计结果却值得怀疑。我们的估计结果和Yau和McGILCHRIST (1998)的回归系数估计结果比较接近，但是θ和φ的估计差别比较大，原因还有待于进一步研究。

结论和进一步的研究方向

本文针对包含右删失的重复观测的纵列生存数据，考虑到同一个体的重复观测的生存时间问题，在Cox比例危险模型的基础上，建立了AR(1)结构的随机效应模型，推导了等级似然函数，并且和REML、ML方法进行了比较，证明了θ和φ的REML的迭代公式正是调整的集中化等级轮廓似然对θ和φ的一阶导数为零形成的迭代公式。本文进一步的研究工作是将本文提出的针对AR(1)随机效应的比例危险模型进行模拟研究，并探讨检验随机效应是否存在AR(1)结构的合适的方法。

参 考 文 献

1.Yau K,McGilchrist C.ML and REML estimation in survival analysis with time dependent correlated frailty.Statistics in Medicine，1998，17(11):1201-1213.

2.Lee Y,Nelder JA.Hierarchical generalized linear models.Journal of the Royal Statistical Society.Series B (Methodological)，1996:619-678.

3.Ha I D,Lee Y,Song JK.Hierarchical likelihood approach for frailty models.Biometrika，2001，88(1):233-233.

4.Ha I D,Lee Y,Song JK.Hierarchical-likelihood approach for mixed linear models with censored data.Life time data analysis，2002，8(2):163-176.

5.Ha I D,Lee Y.Multilevel mixed linear models for survival data.Lifetime Data Analysis，2005，11(1):131-142.

6.王宁宁,徐淑一,方积乾.脆弱性模型的随机效应检验和推广的拟合检验.中国卫生统计，2009，26(1):2-6,10.

7.徐淑一,王宁宁.竞争风险下纵列数据的随机效应建模和估计.中山大学学报(自然科学版)，2007，46(1):7-10.

8.徐淑一,王宁宁.竞争风险下我国住房抵押贷款风险的实证研究.统计研究，2011，28(2):45-52.

9.徐淑一,王宁宁,王美今.竞争风险下纵列持续数据随机效应模型的估计与模拟研究.数理统计与管理，2009，28(6):1013-1023.

10.徐淑一,王宁宁,王美今.基于持续期数据的我国住房抵押贷款违约和提前还款风险分析.南方经济，2009(6):34-43.

11.Wang N,Xu S,Fang J.Hierarchical likelihood approach for the Weibull frailty model.Journal of Statistical Computation and Simulation，2011，81(3):343-356.

12.Breslow N.Covariance analysis of censored survival data.Biometrics，1974:89-99.