需求随机依赖库存环境下的订货仿真优化模型

欧 剑，闵 杰

OU Jian,MIN Jie

安徽建筑大学 数理系，合肥 230601

Department of Mathematics&Physics,Anhui Jianzhu University,Hefei 230601,China

1 引言

库存控制是供应链管理的一个关键因素，库存控制策略的优化可以极大地优化整个供应链的成本和利润水平。现实环境中需求通常不是确定和静态的，而是具有随机性和动态性。目前关于随机需求库存模型的研究方法按照优化目标形式和求解方式总体上分为三类。第一类是在需求服从某种随机分布的假设下，推导出赢利或成本的数学期望的函数表达式，然后利用解析的方式求出极值点，亦即最优订货策略。这类方法在对订货周期内受随机需求影响的库存成本和缺货成本建模计算时通常采用两种方法：（1）用某一时间点（期初或期末）的库存量或者某几个时间点库存量的函数来近似整个周期的平均库存量[1-2]，这类方法简单易行但误差较大。（2）应用微元法精确计算实时的库存和缺货成本[3]，这类方法结果精确但优化目标函数形式复杂、求解困难。第二类研究方法针对解析推导的目标函数难以求解的问题，应用进化计算、模拟退火等智能算法对目标函数进行寻优[3]。这两类研究方法都是用数学方法推导出目标函数的解析表达式。但是，一旦随机需求量服从的分布稍加改变，原有的解析模型就不再适用，而且，考虑更多复杂因素的订货模型往往难以推导出显式的目标函数。因此，前两类解析方法在求解效果和效率上往往不是十分令人满意，在实际的供应链决策中应用起来具有较大的缺陷。

为了解决上述问题，很多研究者提出了通过系统仿真评价订货模型、采用智能算法优化订货策略的第三类方法，如胡幼华、潘荫荣等[4]建立了随机性的批量制造库存系统的仿真模型，Burcu B.Keskin和Sharif H.Melouk[5]设计了随机库存系统的基于分散搜索的启发式优化方法，阴艳超、郭成[6]提出了一种启发式动态响应算法实现对随机需求提前期环境下的库存系统的优化，Ming-Feng Yang，Yi Lin[7]提出用非线性粒子群优化算法求解多级库存系统的最优库存策略。

但是，在目前关于随机库存的研究文献中，均没有考虑需求随库存水平动态变化这一客观现象。自从20世纪70年代以来，许多供应链管理学家都发现，在超市之类的零售系统中库存商品展示得越多，顾客的购买欲望就越强，需求量就越大。这种商品库存促进销售的模式称之为“需求依赖于库存”。关于需求受库存水平影响的形式主要有两大类。第一类是将需求率看成初始库存水平的函数，Gupta和Vrat[8]首次在库存模型中考虑并用需求函数反映了这一规律。第二类是将需求看成是当前库存水平的函数。Mandal[9]首次将需求率假设为库存水平的线性函数，而Baker和Urban[10]提出了需求率是库存水平的多项式函数，该模型能够较准确地表现需求与库存的关系，因此在其后被其他模型广泛采用。Karabi等人[11]又假设了需求率是分阶段的，开始时的需求率是当时库存水平的多项式函数，当库存水平下降到一定值时需求率就变成常数。闵杰等人[12]研究了需求依赖库存和通货膨胀环境下考虑不同缺货策略的库存模型，但是以上这些模型都没有考虑到随机需求的情形。

本文建立了需求随机依赖库存的订货模型并通过基于仿真的进化算法进行求解。首先，假设需求是当前库存水平的单调非减函数，即库存水平越高，需求率相应越高。然后，用计算机仿真的方法观察库存模型的平均赢利水平，评价订货策略。最后，由于仿真方法不存在显式的目标函数，因此将其与进化计算相结合，对订货策略进行优化。

2 需求随机依赖库存的（Q，T）型订货模型

2.1 模型假设与符号

（1）补货是瞬时完成的；

（2）最大库存水平为Q，订货周期为T；

（3）t时刻的库存水平记为I（t），需求率记为D（t）；

（4）单位购买成本为c，销售价格为p，单位时间（一天）单位物品的存储成本为h，一次订货固定成本为A；

（5）允许缺货，单位时间（一天）单位物品的缺货成本为d；

（6）第t0天库存降为零。

2.2 允许短缺的随机（Q，T）订货策略

（Q，T）库存控制策略是一种定期订货策略，即每隔T时刻订货一次，将库存瞬时补充到最大库存水平Q。如果存在缺货销售，则还需将累积的短缺需求补足。如果需求量是随机的，则库存水平的下降速度是动态随机变化的。一个订货周期结束时的库存可能存在三种情况：（1）库存为零，即库存Q在一个周期内恰好销售完；（2）库存大于零，即存在剩余库存；（3）库存为负，即存在由缺货销售累积的短缺需求。整个系统的库存水平变化过程如图1所示。

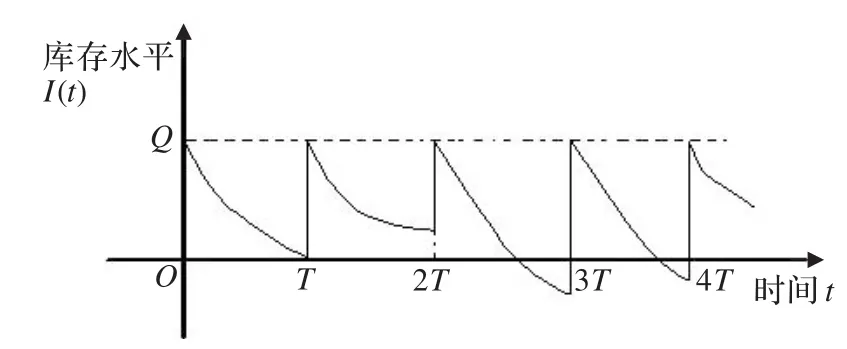
图1 瞬时补货的库存水平随机变化示意图

2.3 需求是库存函数的订货模型及改进

传统的随机库存模型假设需求是随机变量，而其所服从的分布在整个订货周期是固定不变的。但在实际环境中，某一时刻的需求率通常是受到当时库存水平的影响，库存越多，需求越大。1988年，Baker和Urban[10]在库存模型中重新考虑了库存水平对需求的影响方式，修正了之前需求是库存的线性函数的简单假设，而是假定需求率是瞬时库存水平的多项式函数。这类多项式需求函数的形式为：

其中，α＞0，称为规模参数；0＜β＜1，称为形状参数。式（1）表明，随着库存水平的降低，需求率加速减小；当库存水平降至零库存，需求率趋于零，即没有需求。

但是，由于允许短缺，即在缺货的情况下仍然可以销售，因此可以假设零库存时的需求率为D0＞0。显然，库存水平大于0时的需求率应大于D0，因此，可将需求函数修改为如下形式：

2.4 需求依赖库存的随机（Q，T）模型

假设需求是随机的，且依赖库存水平，即库存水平越高，需求率总体上就越大，则式（2）修改为 D(t)=αI(t)β+D0+ε，其中ε为随机波动。

因此，随机需求的数学期望值随着库存水平的增高而变大。不妨假设单位时间（一天）的随机需求量服从参数为λ的泊松分布，因为泊松分布的期望即为参数λ，所以有如下规律：

其中，λ(t)表示第t天的需求量D(t)所服从的Poisson分布的参数，λ0表示零库存时一天的随机需求量D0所服从的Poisson分布的参数。式（3）表明随着销售的进行，库存I不断降低，随机需求量的均值λ随着库存I的降低而减小，直至库存降为零后，在缺货期间随机需求的均值恒定为λ0。不妨假设第t0天库存降为零。

在上述假设下，（Q，T）型订货模型的单位时间（一天）内平均利润的数学期望ATP具有如下计算形式：

本文的目标是确定最优的订货周期T和最大库存水平Q，使该系统单位时间（一天）内的平均利润的数学期望达到最大。

3 离散事件系统仿真

3.1 计算机仿真

近年来，人们所研究的系统越来越复杂，系统构成因素复杂且相互关联，因此很难对系统建立解析模型，即使建立了数学模型也难以求解。而计算机仿真的方法由于不需要进行数学解析，可以考虑各种复杂因素，随意地调整系统结构和参数的随机分布，从而能更贴切地、动态地反映出系统运行的实际特征。因此，通过计算机仿真结合统计的方法可以对系统性能进行有效的评价。

在本文研究的订货模型中，由于随机需求D(t)依赖库存水平 I(t)，而I(t)=I(t-1)-D(t-1)，即t时刻之前的需求影响到t时刻的库存和需求，因此随机变量D(t)和I(t)(t=1，2，…，T)相互不独立，所以订货模型的平均利润的期望式（4）很难以解析形式表示出来。因此，用计算机仿真的方法对（Q，T）型订货策略下的平均利润水平进行评价是一种合适的手段。

3.2 订货模型的离散事件系统仿真

很多实际的库存系统中，需求量是离散的随机变量，库存水平不是连续变化的，而是在离散时间点上改变的。因此可用离散事件系统仿真的方法模拟随机库存系统的运行。离散事件系统仿真有事件步长法和时间步长法两种仿真策略[13]。时间步长法就是按照时间流逝的顺序，一步一步地对系统的活动进行仿真，在整个仿真过程中时间步长保持不变。仿真时钟每步进一次，就对系统中所有的实体、属性和活动进行一次全面的扫描，按照预定的目标记录、计算系统状态的变化，直至仿真时钟结束为止。

本文研究的（Q，T）订货模型假设需求是离散型随机变量，且订货周期是固定的，因此可以建立时间步长法的离散系统仿真模型，以一天为时间步长进行仿真。首先检查当天是否为订货日期，如果是则将库存量刷新为最大库存Q，累计上一次订货费；如果不是，则库存量不变。接着按照式（3）确定随机需求量服从的随机分布的参数，产生当天的需求值，计算当天的收益。若库存量大于需求量，则将库存量减去需求量，计算当天的存贮费用；反之，则累加上缺货量，计算当天的缺货费用。当仿真完成N（充分大）个周期后，用累计的收益减去累计的订货费、存贮费、缺货费，得到净利润，然后除以仿真天数得到平均利润的仿真值。这一仿真过程的流程如图2所示。

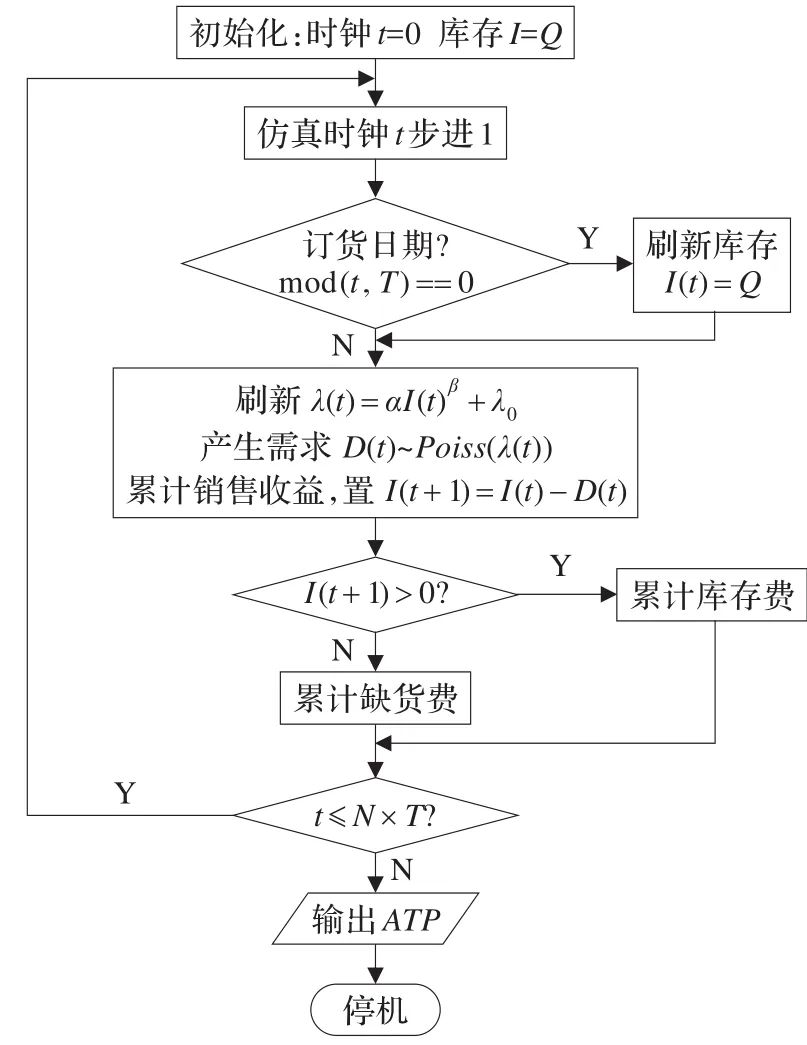
图2 （Q，T）订货模型的仿真流程框图

4 基于仿真的进化计算

4.1 进化计算

进化计算[14]（Evolutionary Algorithm，EA）是一种模仿生物进化机制的智能优化算法，它模拟生物群体的自然选择、杂交、突变等进化形式，采用选择（select）、交叉（crossover）、变异（mutation）三种遗传算子，对编码的解群体进行进化操作，指导种群向最优解方向搜索。进化算法具有并行计算、自组织、自适应、自学习等良好的特性，更重要的是，进化计算不会受到搜索空间限制性条件（如连续、可导、单峰）的约束，不需要其他辅助信息（如梯度、海塞矩阵）。因此，进化计算不仅寻优效率较高，而且相较传统优化算法更加简单、易行、通用。

本文所研究的需求依赖库存的（Q，T）订货模型，其目标函数是平均利润的数学期望，由于期望的解析式难以显式表达，因此采用时间步长法的离散事件系统仿真得到在某一具体的（Q，T）参数下平均利润期望的近似值。所以，既然没有显式的目标函数表达式，那么，传统的依赖梯度的优化方法就不再适用，而基于仿真的进化计算[15]则不会受到目标函数的局限，可以很好地解决该模型的优化问题。

4.2 编码和适应度函数

需求随机依赖库存的（Q，T）订货模型的决策变量是最大库存Q和订货周期T。在进化计算中采用实数编码方案，取控制变量（Q，T）作为进化个体的编码。

适用度函数表明解个体的优劣性，一般是由目标函数转化而成。因为（Q，T）订货模型优化的目标是平均利润的期望最大化，所以，将个体（Q，T）作为系统仿真控制参数，运行离散事件系统仿真模型得到平均利润期望的仿真值，以该仿真值直接作为个体（Q，T）的适用度。

4.3 选择算子

选择操作的目的是从当前群体中以较大概率选出适用度较高的优良个体，进行交叉、变异产生新个体，个体的适用度越高，选择概率就应越大。轮盘赌选择法是一种常见的选择算法，但是当种群中个体适应度（仿真结果）差不多时，不同个体的选择概率相差不大，此时轮盘赌选择就近似于随机选择，起不到优胜劣汰的效果。因此，本文采用Michalewicz的线性排序的选择概率计算公式：

其中i表示个体按适应度从大到小排序的序号。这种选择概率计算公式使得个体之间无论适应度多么接近，都会按优劣顺序拉开被选中概率的差距。q越大，不同个体的选择概率差距就越大，排名靠前的个体被选中的概率就越大，因此，q不应过大，以免较优的少数个体充斥整个种群，造成“早熟”。

4.4 交叉算子与变异算子

交叉操作采用中间重组法，子个体按照如下公式产生：

当s∈(0，1)时，子个体是一对父体的凸组合。如果父代种群是凸集，那么通过交叉产生的子代个体都是这个凸集的内点。

变异操作采用高斯变异算子，变异公式为：

σ2为高斯分布方差，σ2越大，则变异幅度越大。当进化出现“早熟”，种群陷入局部最优解，可通过加大变异幅度使个体跳出局部最优解。

4.5 基于仿真的进化计算结构

进化计算的种群可分为重叠和非重叠两种组织形式，遗传算子可分为重叠和非重叠两种执行方式。本文针对（Q，T）订货模型的特性，设计种群重叠、遗传操作非重叠的进化计算结构如下：

5 基于仿真的模拟退火与粒子群优化

与基于仿真的进化算法类似，基于仿真的模拟退火（Simulated Annealing，SA）和粒子群优化（Particle Swarm Optimization，PSO）等其他基于仿真的优化算法（Simulation Based Optimization，SBO）也可用于随机（Q，T）订货模型的优化。

基于仿真的SA算法如下：

步骤1设定一个初始状态 X=(Q，T)，较高的起始温度t。

步骤2以（Q，T）作为控制参数运行离散事件系统仿真模型，得到平均利润期望的仿真值，取其负值作为X的能量E。

步骤3根据式（7）得到新状态Xnew，并计算ΔE=E(Xnew)-E(X)。

步骤4如果ΔE＜0，则置 X=Xnew；否则，以概率exp(-ΔE/t)置 X=Xnew 。

步骤5 降低温度，t=η×t，0＜η＜1。

步骤6若达到最大迭代次数，则停止，输出X；否则转步骤3。

基于仿真的PSO算法如下：

步骤1初始化N个粒子，每个粒子位置即为一个库存控制变量 X=(Q，T)，在可行域内随机设定初始值和初始速度，k=1，2，…，N 。

步骤2将种群中每个粒子的位置（Q，T）输入离散事件系统仿真模型，得到平均利润期望的仿真值作为粒子的当前评价值。

步骤3更新粒子的当前最好位置Pk和全局最好位置Gbest。

步骤4根据式（8）和式（9）改变粒子的速度和位置。

步骤5如果达到最大迭代次数，则停止，输出Gbest；否则转到步骤2。

6 仿真实例及其分析

6.1 进化计算的实例分析

假设单位货物售价 p=10，购买成本c=5，单位货物单位时间存贮成本h=0.6，缺货成本d=0.7，一次订货成本 A=80，规模参数 α=1.5，形状参数 β=0.4，单位时间需求量 D～Poisson(λ)，缺货时的需求率λ0=20。

设置仿真长度=100个周期，选择概率系数q=0.1，交叉概率=0.5，变异概率=0.1，交叉点s=0.618，高斯变异标准差σ=1，种群规模N=20，进化代数=20，得到库存控制策略的进化曲线如图3所示。由图3易见，从第1代到第3代种群的整体适应度迅速提升，说明进化算法在进化初期的收敛速度很快，种群迅速向最优个体集中。当进化到第14代，最优适应度不再提高，种群整体适应度则始终缓慢提升。

图3 进化过程中适应度曲线图

进化完成后得到平均利润最优的5个订货策略如表1所示。从表1中可以看到，如果要提高服务水平，降低缺货率，则必须提高最大库存Q值，或缩短订货周期T，从而导致平均利润降低。因此，在实际的需求随机依赖库存的（Q，T）订货模型中要综合考虑盈利水平和服务水平，作出最佳的订货策略。

为考察模型参数对最优解的影响，通过分别改变参数λ0、α、β的数值来进行模型灵敏度分析，结果列于表2。

表1 仿真结果（每天平均利润）

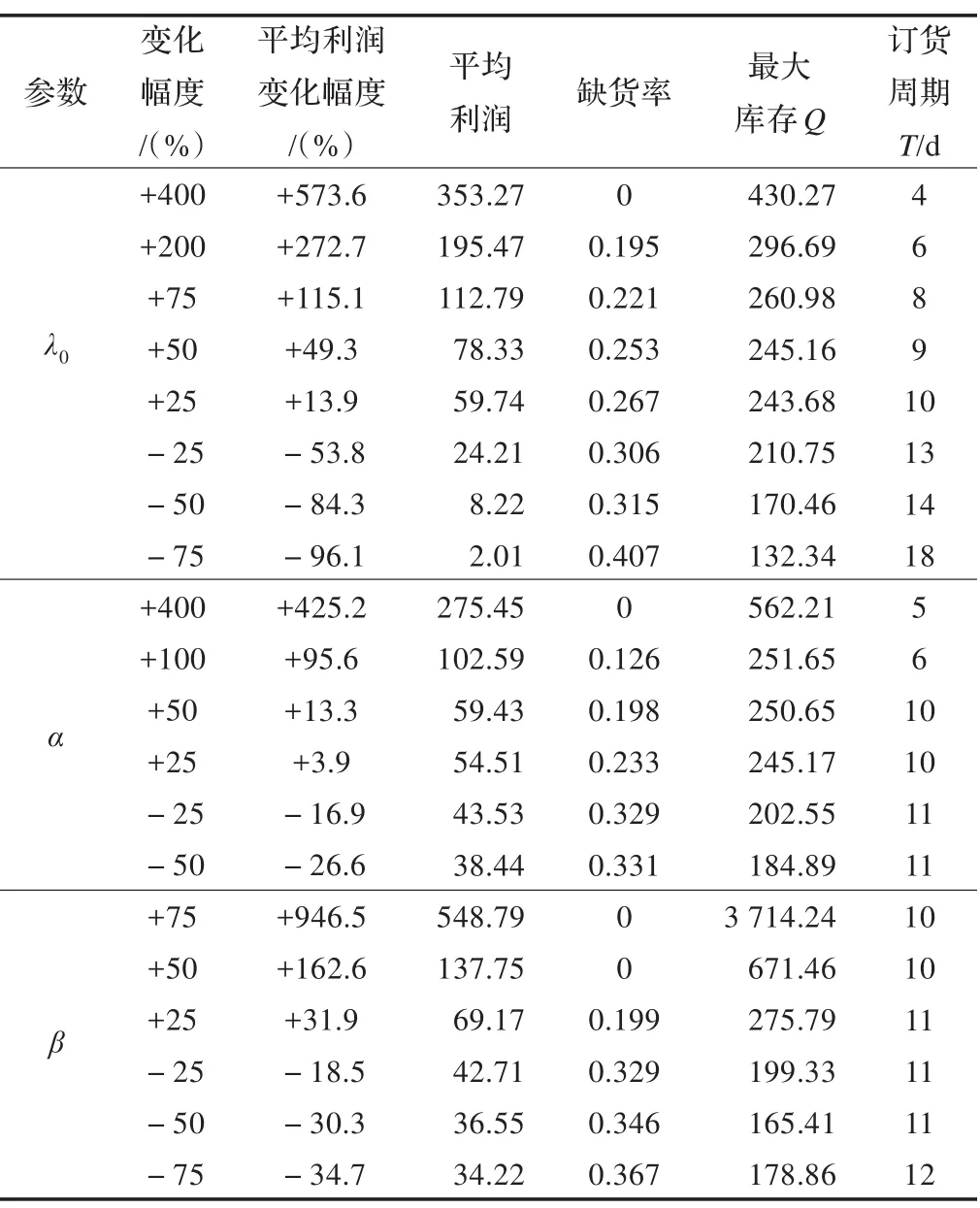
表2 模型的灵敏度分析

由表2易得如下结论：（1）缺货期平均需求率λ0、规模参数α和形状参数β越大，则最优的平均利润水平越高，最优的最大库存水平Q越大，最优的订货周期T越小，缺货率越低，这说明需求率越高或需求依赖库存效应越明显时，利润水平越高，最优订货策略越倾向于高库存、短周期、现货销售。（2）最优订货周期T对α和 β的改变不是非常敏感，对λ0较敏感。（3）最大库存水平Q对 β的改变较λ0和α更敏感。

6.2 不同SBO算法对比分析

用模拟退火算法优化该实例，取初始退火温度为1000，冷却系数η=0.95，得到能量下降曲线如图4所示。退火算法在迭代到495次时收敛到最小值－52.8592。

用粒子群算法优化该实例，设置粒子群规模N=20，最大迭代次数=20，惯性权重w=0.3，学习因子c1=2，c2=1.5。当迭代到11次时平均利润收敛到50.95。

图4 模拟退火的能量下降曲线

由于SBO算法的计算量主要是仿真的计算量，所以可用仿真的次数来度量算法的计算量。因为EA、PSO和SA算法在每次产生新解时进行一次仿真评价，所以算法的计算量为种群规模和迭代次数的乘积。三种算法的性能对比如表3所示。由表3可见，EA和PSO算法的收敛速度较快，而SA算法为了避免陷入局部最优则需迭代较多次数。因此，针对本文的随机库存优化模型，基于仿真的EA和PSO算法均为效率较高的优化方法。

表3 三种算法的计算量对比表

7 结束语

本文建立的需求随机依赖库存的订货模型反映了实际库存系统中需求的随机性和动态性。由于该模型中平均利润的数学期望难以解析表示，所以无法通过传统的优化方法求得最优订货策略，而基于离散事件系统仿真的进化算法则可以较好地解决这一优化问题，该算法不仅具有较高的运算效率和灵活性、通用性，而且可以获得多个候选策略以供决策者综合权衡选择。但本文的进化计算仅将单位时间的平均利润最大化作为进化目标，即只把平均利润作为适应度函数，而实际决策时不仅要考虑利润最大化，还要考虑服务质量，即缺货率尽可能低，因此如何设计高利润和低缺货率的多目标优化算法是下一步的研究目标。

[1]Feng Cheng，Sethi S P.A periodic review inventory model with demand influenced by promotion decisions[J].Management Science，1999，45（11）：1510-1523.

[2]Bookbinder J H，Cakanyildirim M.Random lead times and expedited orders in（Q，r）inventory systems[J].European Journal of Operational Research，1999，115（2）：300-313.

[3]纪鹏程，宋士吉，吴澄.随机需求和提前期环境下的精确库存成本建模[J].计算机集成制造系统，2008，14（11）：2129-2133.

[4]胡幼华，潘荫荣，房爱莲.随机性的批量制造库存系统的仿真模型[J].计算机工程，2003，29（8）：70-71.

[5]Keskin B B，Melouk S H，Meye I L.A simulation-optimization approach for integrated sourcing and inventory decisions[J].Computers&Operations Research，2010，37（9）：1648-1661.

[6]阴艳超，郭成.不确定环境下的一种动态响应库存优化方法[J].计算机工程与应用，2012，48（17）：238-242.

[7]Yang Mingfeng，Lin Yi.Applying the linear particle swarm optimization to a serial multi-echelon inventory model[J].Expert Systems with Applications，2010，37（3）：2599-2608.

[8]Gupta R，Vrat P.Inventory model for stock-dependent consumption rate[J].Opsearch，1986，23（1）：19-24.

[9]Mandal B N，Phaujdar S.An inventory model for deteriorating item and stock-dependent consumption rate[J].Journal of the Operational Research Society，1989，40（5）：483-488.

[10]Baker R C，Urban T L.A deterministic inventory system with an inventory-level-dependent demand rate[J].Journal of the Operational Research Society，1988，39（9）：823-831.

[11]Karabi P，Datta T K，Chaudhuri K S，et al.An inventory model with two-component demand rate and shortages[J].Journal of the Operational Research Society，1996，47：1020-1036.

[12]闵杰，欧剑，周永务.通货膨胀环境下需求依赖库存的经济订货批量模型[J].计算机集成制造系统，2010，16（2）：299-309.

[13]肖田元，张燕云，陈加栋.系统仿真导论[M].北京：清华大学出版社，2000.

[14]Jones M T.Artificial intelligence[M].北京：电子工业出版社，2009：116-117.

[15]李东，汪定伟.基于仿真的优化方法综述[J].控制工程，2008，15（6）：674-677.