基于滚动规划的泊位和岸桥分配集成模型研究
白治江,黄 卿
BAI Zhijiang,HUANG Qing
上海海事大学 信息工程学院,上海 201306
Information Engineering College,Shanghai Maritime University,Shanghai 201306,China
1 引言
集装箱码头的生产效率是由相互影响的若干处理过程决定的,对于岸边的处理包括泊位分配、岸桥分配以及岸桥调度问题,其他重要的处理过程包括堆场规划,积载规划和人力规划等。Stahlbock和Vop综述了集装箱码头的所有操作过程[1],Bierwirth和Meisel专门论述了泊位分配和岸桥调度问题[2]。Lai和Shih按照先到先服务的原则提出了一个泊位分配的启发式算法[3]。若两艘货轮竞争同一泊位时,就必须在平衡成本的前提下考虑它们的优先权。影响优先权的因素有很多方面,如操作的便利性,盈利效益,负载量大小,紧急情况,海浪情况,集装箱的转运情况等。Legato和Mazza指出了货轮接受服务的优先权问题[4],其解决方案是为重要货轮预留专用泊位,但这种方法不仅增加了调度的复杂性,也无法有效提高码头的总体服务水平。合理的方案应该是让优先权高的货轮尽可能地靠近其首选泊位即可。Imai提出通过附加权重实现优先权的方案[5],比如某货轮因紧急情况需要尽快处理,则只须在模型求解时增大其权重值,则规划方案就能实现高优先权。Lokuge和Alahakoon的方案是让高优先权的货轮等待时间为0,确保它们能够随到随服务[6]。除了优先权对货轮处理时间的重要影响外,货轮的泊位和配置的岸桥数也是影响处理时间的重要因素。Moorthy和Teo提出了处理首选泊位问题的框架结构[7],并阐述了首选泊位对堆场存储规划,人员和设备调度等的重要影响。Park和Kim的整数规划模型同时考虑了货轮优先权和首选泊位问题[8],优先权通过在目标函数中施加延误惩罚值的办法实现。模型用两阶段法求解,第一阶段确定每个时段内货轮的泊位以及配置给每个货轮的岸桥数,第二阶段实现每个岸桥的任务规划(该阶段实际上是操作层面的决策问题,所以本文只考虑第一阶段的问题)。Liu等在先行优化BA方案的基础上再求解QCA问题[9]。QCA确定了配置于货轮的岸桥数量,因而也决定着货轮的处理时间以及总的泊位占用时间,而处理时间和泊位占用时间又是BA问题的关键输入,所以将BA和QCA集成优化能够体现总体优化效果。
本文对码头作业的基本假设如下:
(1)岸边看作一个连续的线段,采用连续泊位建模规则。
(2)岸桥可以在泊位之间自由移动。
(3)每一个岸桥一旦准备就绪立即开始作业。
(4)货轮负载量是其装卸集装箱的总量。
(5)处理时间是装卸的总时间(包括延误在内)。
(6)货轮一旦锚定,则服务期间不再移动,但岸桥可以移动。
2 BA和QCA的集成模型
本章建立了一个BA和QCA的集成模型,目标是使所有集装箱货轮的调度费用最小,模型中同时考虑了优先权,首选泊位,岸桥移动等生产中的实际特征。货轮最好的停泊位置(即首选位置)就是距离装卸集装箱的存放位置最近的泊位,如果停泊位置距离首选泊位太远将增大集卡运送距离,所以实际泊位与首选泊位距离应最小化。
为了将本规划问题建成混合整数模型,把时间轴离散化为等距离的时段,岸桥的配置和变动均以时段为单位进行。正如本文实验中将要说明的一样,时段的具体长度由用户根据实际情况确定。
2.1 滚动规划结构
滚动规划结构是实现规划的策略。当某特定时刻(例如早上6点)求解模型时,须限定规划的时间跨度(如24 h或48 h),该时间跨度简称规划期,规划期被离散化为相等的若干时段(如2 h为一个时段)。求解模型获取当前规划期中第一个时段(如6点至8点)的执行方案。在第一时段末(8点),利用已经更新的数据(如参数arr(i),mst(i),epd(i),ddl(i)的值会相应递减)将同一模型又重新求解一次,从而在时段数相同的新规划期内生成第一时段(此时的第一时段是8点至10点)的执行方案,即每运行一次模型相当于规划期向前滚动一个时段。
滚动规划结构会增加模型实现的复杂度。首先,在做新规划时,有些货轮的服务已经开始,所以它们的停泊位置不允许改变,但这些货轮在下一时段的岸桥数仍可改变。从模型的角度而言,这些货轮的相关参数busyi1,pli,dli,dri已经固定不变,但负载wl(i)却必须更新。其次,对那些最后离港期限或最早离港时间超出规划期范围的货轮,要在模型的约束条件中做特别的规定。上述这些情况在下文解释模型时将做具体说明。
2.2 模型建立
模型中所使用参数记号如表1所示(凡涉及时间的,均以时段为度量单位)。
决策变量如表2所示。
基于滚动规划结构的混合整数线性规划模型如下所示。目标函数一共由4项组成,其中前三项分别对应着处理时间延误代价,泊位偏差代价和移动岸桥的代价;第4项是与滚动规划有关的修正值。下面分别进行详细说明:目标函数第一项是货轮处理时间延误的惩罚项。当货轮靠泊并立即以最大岸桥数开始服务,则各个连续时段起始点的负载余量称为理想负载余量irw(i,t),最小服务时间mst(i)就是当irw(i,t)降为0时所需的时段数。显然,各个后续时段的实际负载余量大于或等于irw(i,t)。在时段 epd(i)=arr(i)+mst(i)上,理想负载余量已经降为0,但由于泊位和岸桥条件的限制,实际负载余量一般并不为0,这表示货轮服务已经延误。目标是要使延误最小化,也就是使从时段epd(i)开始往后各个时段的负载余量总和最小化,并且与理想负载余量偏差越大,接受的惩罚也越大,因此再给延误总量乘以优先处理系数α(i),于是当两个货轮同一时刻竞争岸桥时,优先权能保证更重要(或延误更多)的货轮获得相对多数的岸桥以便尽早完成处理。目标函数第二项是货轮停泊位置偏离首选位置的惩罚项,dli和dri分别表示与首选泊位的左偏差和右偏差,该偏差先与货轮相应负载量wl(i)相乘,以表示内卡装卸每个集装箱时都要运行这段额外的偏差距离。此项再进一步乘以位置优先系数β(i),用以反映货轮的首选泊位相对于处理时间(目标函数的第一项)的重要性。
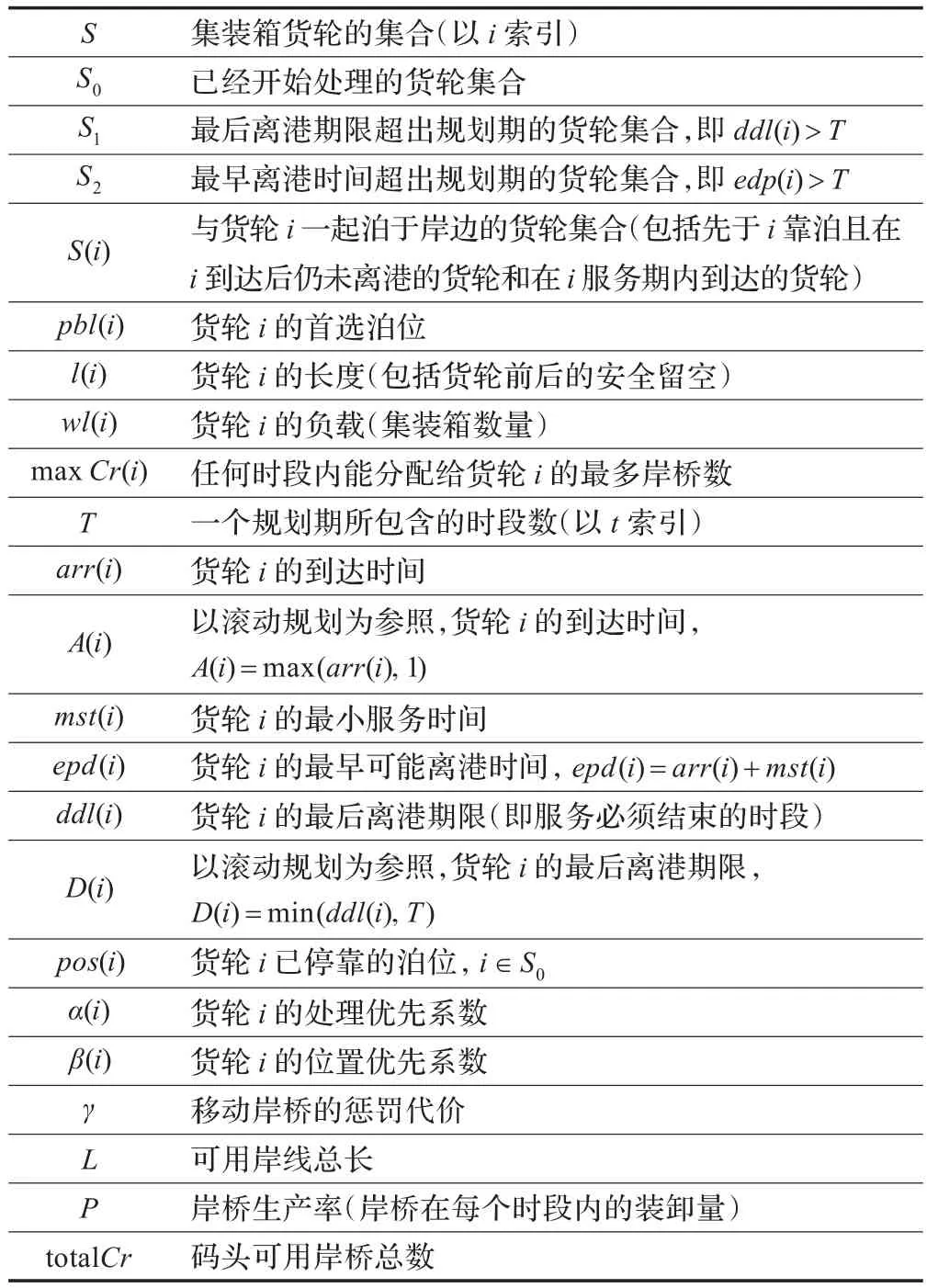
表1 模型中所使用参数记号

表2 决策变量
目标函数的第三项是货轮服务期间岸桥配置数量变化的惩罚项,反映了岸桥移动的机会成本。规定只有当货轮的岸桥数增加时才计算此惩罚项,因为当岸桥减少时,要么是货轮服务结束(当然不能罚),要么岸桥移到另一个货轮(惩罚值在接受岸桥的货轮上计算)。目标函数第四项是与滚动规划有关的修正项。对于那些最早离港时间超出T的货轮其延误惩罚并未包含在目标函数的第一项中,这意味着模型可以把此类货轮的服务延迟到T之后而无须承担任何代价,其好处是能为优化其他货轮的调度提供更大余地。但如果在当前规划期内完全不考虑epd(i)超出T的货轮,则可能在后继的规划中付出更大的代价。所以在目标函数中增加修正项rwiT作为对这些货轮延误的惩罚,从而使它们也参与到当前规划期的调度当中。
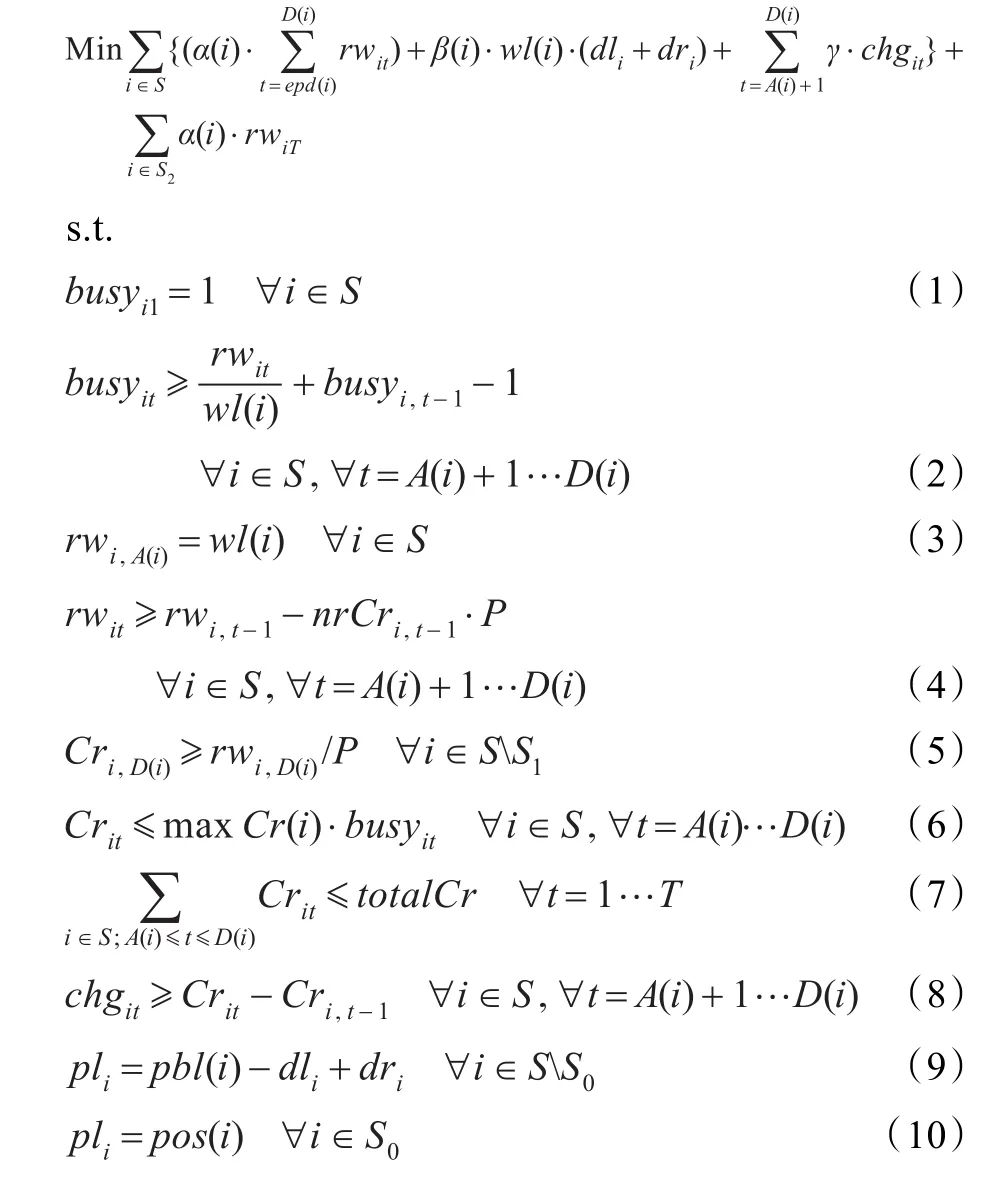
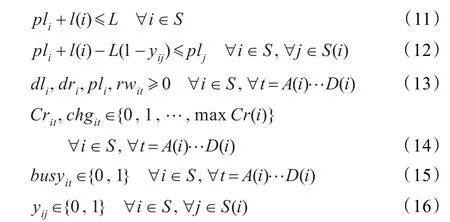
约束条件式(1)表示货轮i正在接受服务;式(2)将二值变量busyit与rwit联系起来,一旦开始,只要负载余量不为0,处理就一直继续;式(3)定义货轮的初始负载;式(4)货轮i在下一个时段的负载余量等于前一时段之负载余量减去该货轮岸桥数乘以岸桥生产率,不等式确保rwit非负;式(5)规定货轮处理的最后期限(ddl(i)>T的货轮除外);式(6)任何时刻实际配置于货轮的岸桥数不能超过所允许的最大值;式(7)任何时段,岸边布局的岸桥数小于等于岸桥总数,式(8)定义变量chgit为货轮i从某时段到下一个时段岸桥的增加数。若岸桥数不变或减少时,chgit=0;式(9)货轮实际泊位由相对于首选泊位的左右偏差确定;式(10)处于服务中的货轮泊位固定不变;式(11)所有货轮泊位须在可用岸线长度范围内;式(12)保证不能在相同位置同时服务两个货轮;式(13)规定决策变量非负属性;式(14)定义整型变量;式(15)和式(16)定义二值变量。
2.3 示范例子
本示范例子用以说明模型的工作原理,所使用的相应数据如表3所示。设有5个货轮,岸线长1 200 m,15个岸桥,生产率为30箱/h,时段长为1 h,γ设为150。
本示范例的解决方案如图1所示,其中三类惩罚值均有发生(如表4),货轮2和3在第7和第8时段未分配到最大岸桥数因而产生延误罚值,服务结束时间延误一个时段,例如对货轮2,本来在第10时段理想负载余量为150,在第11时段(即最早离港时段)为0,由于在第7和第8时段只配置了3个岸桥,则货轮2的服务迟滞了120个集装箱,使得在第10和第11时段的实际负载余量分别为270箱和120箱,引起的延误罚值为9×120=1 080,货轮5的延误惩罚值是因为开始服务时间延迟(必须等货轮4离开)。
第二类惩罚值是偏离首选泊位引起的,只有货轮1和4在首选泊位,剩余的货轮只有等别的货轮离开后才有可能得到首选泊位,但这将导致非常高的延误罚值。模型在不同代价之间寻找最优平衡的结果是:虽然达不到首选泊位,但尽快靠泊是代价较小的选择。
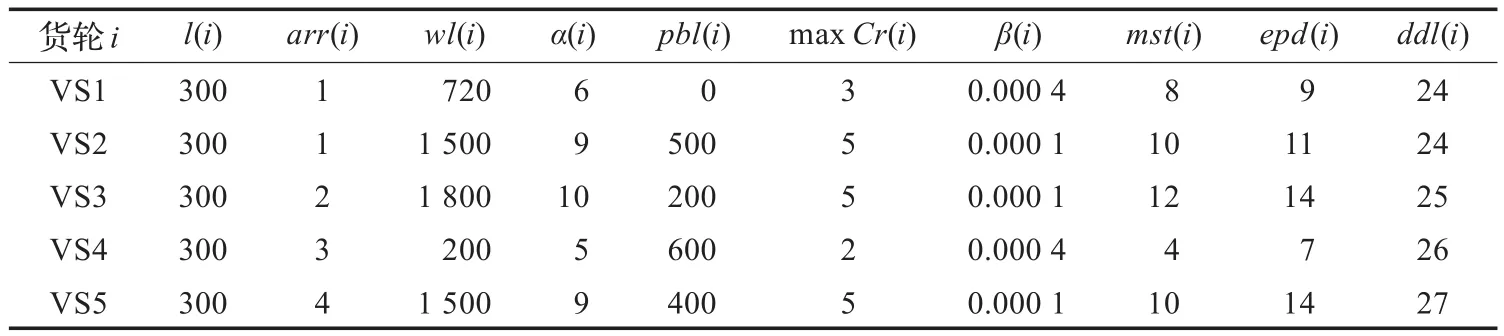
表3 示例中的船数据
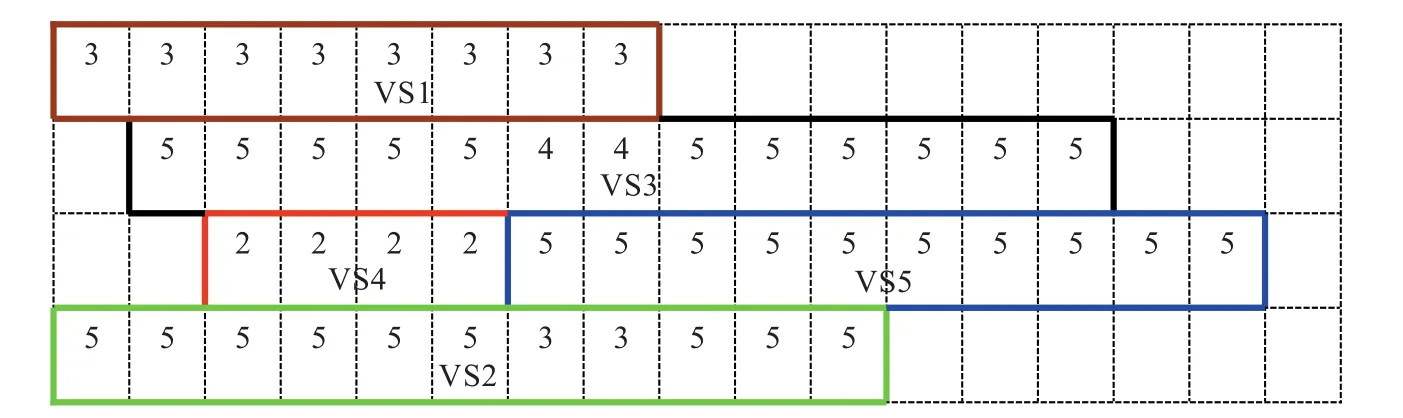
图1 示例的解
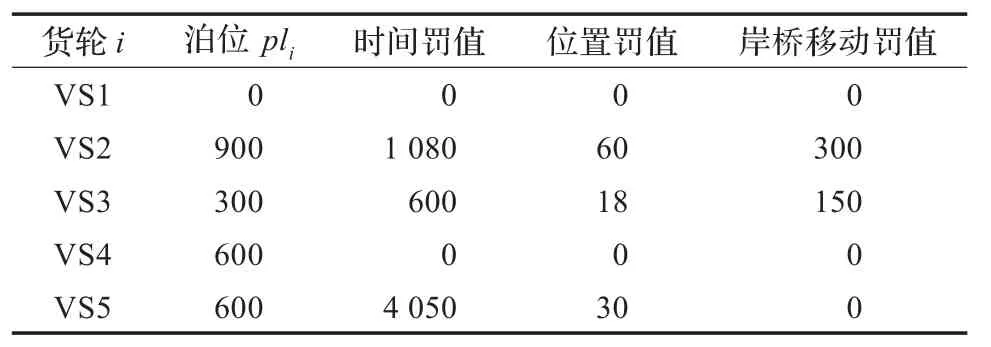
表4 示例中的惩罚值
为了限制服务期间货轮的岸桥数量变化,增加岸桥将导致惩罚值,所以货轮2和3在第9时段有岸桥增加的罚值。
3 实验结果
为了验证模型及滚动规划结构的有效性,采集到上海港某码头一个季度的运行数据集,如表5所示。码头的岸线长度近似为2 000 m,岸桥数为18台。负载即为所有待装/卸集装箱总量,货轮数量为782,总负载量为669 503。

表5 实验数据
实验中将岸桥生产率设为35箱/h,虽然实际生产率高于这个值,但考虑到岸桥移动所造成耽误的事实,特意将其降为35。货轮的位置优先系数β(i)取为0.000 1,这个微小取值能保证目标函数中对位置偏差的惩罚相对于延误惩罚仍然很小。
模型用C++(使用ILOG Concert Technology技术)编码实现,用Cplex 12求解。
3.1 基本情况分析
首先通过实验确定适合该数据集的时段长度和规划期长度,所以在数据集上以不同的时段(2,4和8 h)与不同的规划期(24,48和72 h)来运行模型。
表6最后两行列出了不同组合下模型每次迭代的CPU平均值和最大值,正如所料,在小时段且大规划期组合的情况下运算复杂度增加。从CPU的值得到的重要结论是,即使对最复杂的72 h规划期与2 h时段组合的平均计算时间也非常有限(说明:在运算期间需要通过逐渐增加MIP的相对允许偏差(relative MIP gap tolerance)来限制单次运行的计算时间,例如,运行1 min后cplex相对偏差由默认的0.01%增至0.05%,2 min和3 min后相对偏差分别增大至0.1%和1%。本实验中最大的MIP偏差仅为0.4%,最长运行时间仅为3 min)。由于运行时间如此之短,模型可用于信息更新快并且需要进行频繁重新规划的环境中。
表6剩余部分列出不同组合下的目标函数代价,对比结果发现,在时段长度相同的情况下,24 h规划期的惩罚值一般较大,而48和72 h的惩罚值几乎相同。原因是对当前时段到达的货轮进行规划时,将后续时段到达的货轮考虑进来是有意义的,但显然向前看2天已经足够了,向前看得更远(如3天)计算复杂度增加但解的质量并无提高,所以本文实验中只考虑48 h的规划期。
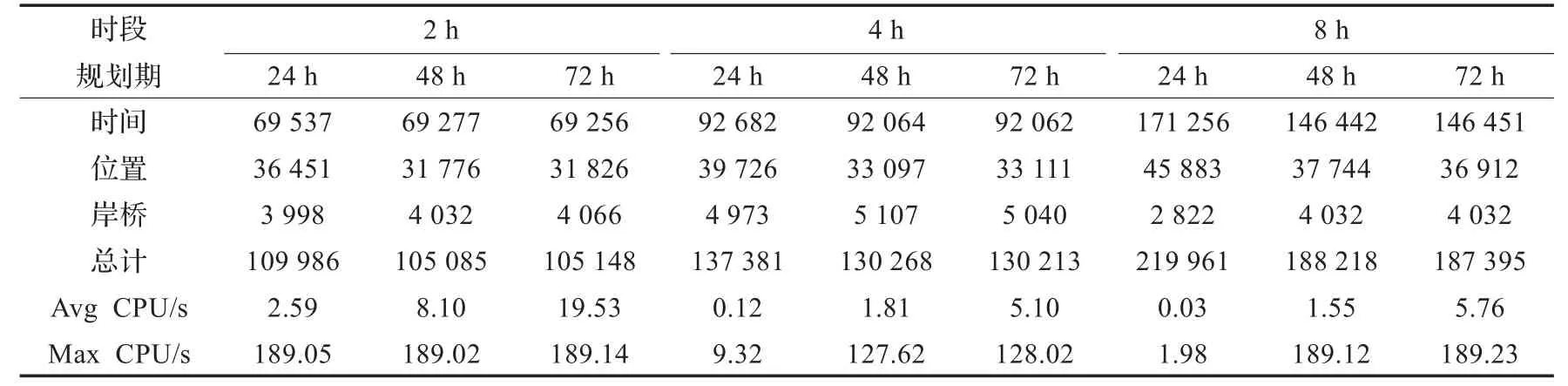
表6 目标函数各组成部分的值和模型的时间复杂度

图2 一个规划的解
当时段长度不同时,规划总代价差距很大,然而解的实际结构(即泊位分配和岸桥配置)却几乎相同。时段长度对总代价影响的原因如下:因为泊位是以时段为基本单位分配的,所以即使完成服务的货轮在某时段内已经离开,但该空闲泊位其他货轮仍不可用。例如假设一个货轮需要6 h服务,若使用2 h时段的话,则3个时段后该位置即为可用。若使用4 h时段,虽然该货轮只需1.5个时段即可完成服务,但必须给其分配2个连续时段,此时在剩余的0.5时段内,该泊位虽然已经空闲但仍不能被其他货轮使用,从而迫使这些货轮或者等待或者停靠不甚理想的泊位,导致时间和距离的相关代价上升。基于实验结果的分析,该码头生成泊位分配和岸桥配置的最合适组合是2 h时段且48 h规划期。
图2是该组合下一次规划的结果,其中V表示货轮,相应的数字表示服务期间每个时段内的岸桥数,水平轴表示当前规划期内的时段,纵轴表示岸线的长度。
3.2 敏感性分析
为了更进一步验证模型的有效性并展示其决策支持的潜力,对可用岸桥数的变化,可用岸线长的变化以及位置惩罚参数β(i)的变化做了敏感性分析,得出如下结论:(1)当岸桥数量增加时,能显著降低总代价,这是因为额外的岸桥能使货轮更快完成服务(避免了时间延误惩罚),从而尽快释放泊位使其他货轮能更靠近首选泊位(减少了位置罚值),岸桥不再为紧缺资源(避免了岸桥移动的惩罚值),减少岸桥数将导致更多拥堵并增加总的调度成本。无论是增加还是减少岸桥数,模型都会在三类成本之间进行寻求优化平衡。(2)当可用岸线长度减少时,会同时增加位置偏差罚值和时间延误罚值,因为岸线长度减少意味着在繁忙时段没有足够空间服务所有的货轮,首选泊位更加没有可能。(3)权重系数β(i)实际上是具有管理意义的参数,因为它决定了如何平衡时间偏差(影响货轮方收益)和位置偏差(影响码头方收益)之间的关系。若β(i)值上升,则货轮首选泊位平均偏差减少,但延误会增加。模型将会在两种代价之间寻找最优平衡。
4 结论
本文介绍了一个泊位分配和岸桥配置的集成模型,包含了优先权,首选泊位和处理时间几个实际生产的特征。该模型能在信息更新的前提下滚动做出优化决策,可用作现代化码头的决策支持工具,从而使规划管理者有更多时间应对意外情况下的调度问题。模型成功地在实际数据上得到了有效性验证,计算结果表明该模型能在合理的时间内给出高质量的规划方案。此外对岸桥数,岸线长度和管理参数的敏感性分析结果表明,模型能有效地对各个代价组成部分进行最优的折中平衡,表现了支持管理决策的能力。模型能在短时间内求解实际案例的规划问题,进一步测试评估将在具有高度拥堵特征的仿真数据上进行,以便检验在极端情况下模型的鲁棒性和灵活性以及是否需要采用启发式方法。
[1]Stahlbock R,Vop S.Operations research at container terminals:a literature update[J].OR Spectrum,2008,30:1-52.
[2]Bierwirth C,Meisel F.A survey of berth allocation and quay crane scheduling problems in container terminals[J].European Journal of Operational Research,2009,202:615-627.
[3]Lai K K,Shih K.A study of container berth allocation[J].Journal of Advanced Transportation,1992,26:45-60.
[4]Legato P,Mazza R M.Berth planning and resources optimization at a container terminal via discrete event simulation[J].European Journal of Operational Research,2001,133:537-547.
[5]Imai A,Nishimura E,Papadimitriou S.Berth allocation with service priority[J].Transportation Research Part B,2003,37:437-457.
[6]Lokuge P,Alahakoon D.Improving the adaptability in automated vessel scheduling in container ports using intelligent software agents[J].European Journal of Operational Research,2007,177:1985-2015.
[7]Moorthy R,Teo C.Berth management in container terminal:the template design problem[J].OR Spectrum,2006,28:495-518.
[8]Park Y M,Kim K H.A scheduling method for berth and quay cranes[J].OR Spectrum,2003,25:1-23.
[9]Liu J,Wan Y W,Wang L.Quay crane scheduling at container terminals to minimize the maximum relative tardiness of vessel departures[J].Naval Research Logistics,2006,53:60-74.
[10]de Oliveira R M.Clustering search for the berth allocation problem[J].Expert Systems with Applications,2012,39:5499-5505.
[11]Buhrkal K,Zuglian S,Ropke S,et al.Models for the discrete berth allocation problem:a computational comparison[J].Transportation Research Part E:Logistics and Transportation Review,2011,47:461-473.
[12]Chaves A A,Lorena L A N.Clustering search algorithm for the capacitated centred clustering problem[J].Computers&Operations Research,2010,37:552-558.
[13]Cheong C Y,Tan K C,Liu D K,et al.Multi-objective and prioritized berth allocation in container ports[J].Annals of Operations Research,2010,180:63-103.
[14]Cordeau J F,Laporte G.Models and tabu search heuristics for the berth allocation problem[J].Transportation Science,2005,39:525-538.
[15]Giallombardo G,Moccia L,Salani M,et al.Modeling and solving the tactical berth allocation problem[J].Transportation Research Part B,2010,44:232-245.

