基于时延控制的伪码多普勒补偿算法

高述涛

GAO Shutao

湖南外贸职业学院 服务外包学院，长沙 410014

School of Service Outsourcing,Hunan International Business Vocational College,Changsha 410014,China

近年来，随着军民用航空的飞速发展，卫星和用户之间的相对运动、接收机晶振的老化等都会使得接收到的信号含有多普勒，包括载波多普勒和码多普勒[1]。一般情况下，常规的接收机捕获时通常是不考虑信号的码多普勒带来的影响[2-3]。但是对于高灵敏度接收机，就不得不考虑码多普勒的影响，由于码多普勒的存在，高灵敏度接收机本地码和接收信号之间会出现严重的不匹配。在极端的情况下，当伪码多普勒频移所造成的码片之间的不匹配超过半个码片时，增长相干积累时间不仅不会提高增益，反而会降低整个信号的捕获性能。因此，需要对码多普勒进行补偿。

通过消除接收机和卫星的码速率之间的不一致，来补偿码多普勒的影响。根据载波和伪码的比例关系，利用载波辅助伪码，改变载波多普勒搜索步进的同时也实时改变本地伪码生成速率，当载波多普勒完成搜索时，伪码多普勒也实现了补偿。然而，对于在GNSS信号快速捕获中广泛应用的基于快速傅里叶变换（FFT）的信号捕获结构[2]，这种码多普勒补偿方法将使得其实现难度加大。因为改变本地生成码的生成频率就意味着本地码作FFT变换的点数一直在变。同样，这种补偿方法也不适用于基于匹配滤波器的并行捕获结构[4]，这是因为本地码生成频率的持续变化致使匹配滤波器的系数需要不断刷新，这将导致实现结构的复杂以及处理时间的增加。本文提出一种基于时延控制的码多普勒补偿方法，通过延迟滤波器的设计完成码多普勒的补偿，可以不需要改变本地码的生成频率。采用处理损耗评估补偿前后码多普勒对信号捕获的影响。同时，本文也给出了该方法的实现结构，并进行了相应的仿真分析。

1 常规导航信号捕获

导航接收机常规的捕获结构如图1所示[1]，经过ADC采样后的中频信号可以表示为：

其中A表示信号的幅度，D(n)表示导航电文数据，C(n)表示扩频码，fIF表示中频频率，fD表示多普勒频率，w(n)为噪声项，其方差为。

图1 常规导航信号的捕获结构

在不计噪声的情况下，经过中频积累非相关后积累输出的检测量值为：

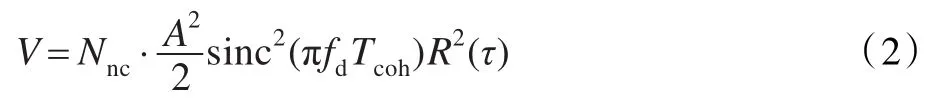
其中，Nnc表示后积累次数，fd表示残留多普勒频率，Tcoh表示相干积累时长，τ表示以码片宽度Tc为单位的码相位延迟，R(·)表示码的自相关函数。可以看出，捕获性能与载波多普勒以及伪码相位误差有关。

相干积分后的积累值I(n)与Q(n)中的噪声均服从正态分布[1]，则式（2）给出的非相干积分后的检测量V服从自由度为2Nnc的卡方分布。

设给定的信号捕获虚警率为PFA，则相应的捕获门限值可以由下式确定：

则对应的检测概率为：

2 基于时延控制的伪码多普勒补偿算法

2.1 伪码多普勒捕获性能分析

接收机的信号捕获过程一般是通过对某颗卫星信号的载波频率和码相位这二维进行扫描式搜索来完成的。通常并没有考虑码多普勒的影响，这在常规情况下是可以容忍的，因为一般情况下码多普勒比较小，而且中频积累时间较短，码多普勒引起的码相位的误差不是很大，对式（2）中的统计检测量的影响较小。但是如果接收信号比较弱，导致需要较长的中频积累时间，这时候码多普勒的影响就不能忽略。为了直观评价码多普勒对捕获性能的影响，参考文献[5]，分析不同中频积累时间下伪码峰值损耗，峰值损耗定义为：

其中，R(τ)为存在码多普勒条件下的相关峰值，R0(τ)为无码多普勒条件下的相关峰值。

存在码多普勒条件下的捕获性能同样可由式（3）及式（4）确定，不同的是其中的非中心参量为：

2.2 算法实现

为了充分讨论码多普勒的补偿方法，这里假设经过下变频及载波剥离后的接收信号没有残余的载波多普勒，功率也进行归一化，在GNSS接收机中，通过伪码数控振荡器（NCO）生成的本地伪码信号可以表示如下：

其中，Tc表示生成伪码信号的周期，Ts表示采样周期，p(t)表示对应卫星的码片波形，xn为对应卫星伪码序列的第n个元素，fd表示码多普勒。

由于多普勒的影响，接收到的信号会出现信号周期的伸张压缩，即接收信号的周期会变大或变小。当相干积累时间一长，本来对齐的伪码相位就会变得不再对齐，这样就会影响相干积累的积累增益。特别是当本地伪码和接收信号的伪码滑动超过半个伪码周期时，继续增加相干积累时间将无益于捕获性能的提升，反而会降低捕获性能。这是因为伪码相位误差超过半个码片后积累的信号功率没有积累的噪声功率强。因此，接收机的采样周期和本地伪码的生成信号的周期需要满足下式：

为了保证本地伪码频率的恒定，根据式（8），接收机的采样频率需要随着多普勒的调整而调整才能满足上式。然而，接收机的A/D转换器通常没有能力实时改变信号的采样率，即所接收的信号的采样率是恒定的。因此，改变采样频率的方法也不可取，通过数字滤波器完成多普勒补偿的方法，不需要改变采样频率。根据式（7），所接收的信号也可以表示为：

本文基于上述原理，提出了一种基于数字时延控制的码多普勒补偿方法，并给出了包括码多普勒补偿在内的新的GNSS信号捕获结构如图2所示。新的GNSS信号捕获结构包括三个部分，即载体剥离，伪码多普勒补偿和相干积累。其中载体剥离和相干积累等操作和传统的捕获结构实现方法相同。码多普勒补偿是通过时延控制实现，包括整数采样点的延迟和分数阶延迟。整数采样点延迟采用先入先出（FIFO）结构的存储器即可实现，而分数阶延迟采用FARROW结构的分数阶延迟滤波器实现。可变分数阶延迟滤波器的设计实现可以参考文献[6-9]中提出的方法，下节将设计所需的可变分数阶延迟滤波器。

图2 具有码多普勒补偿模块的GNSS信号捕获结构

基于时延控制的码多普勒补偿方法需要实时获取时延补偿值，用于补偿不匹配的整数采样点延迟和小数采样点延迟。提出利用NCO的方式获取采样点间的不匹配延迟，其实现结构和常规NCO一致，具体实现可以参考文献[1]，这里不再赘述，仅给出其设计指标。由图2可以看出，NCO输入的累加控制字为2N·fd/fs，累加的溢出值用于控制整数采样点延迟，未溢出累加值用于控制小数采样点延迟。其中，码多普勒的值根据载波和伪码的比例关系来确定，延迟补偿的分辨率为Ts/2N。

2.3 可变分数阶延迟滤波器的设计

文献[6-9]给出了可变分数阶延迟滤波器的设计实现方法，一般流程是根据给出的幅频以及相频特性指标求解滤波器系数以及阶数，是一个非线性的优化问题，求解难度较大。下面先介绍FARROW结构延迟滤波器的基本实现结构，然后给出一种简单可行的设计方案。

FARROW结构的可变延迟滤波器基本原理是采用多项式拟合滤波器系数，设滤波器系数可以表示为下式：

那么滤波器传输函数如下：

其中，子滤波器的阶数为N，多项式阶数为P，该结构示意图如图3所示，可以看出该结构只需要更新时延值就可以实现可变时延的控制。

图3 基于FARROW结构的可变分数阶延迟滤波器的实现结构

3 仿真实验及性能分析

为了评估本文提出的码多普勒补偿方法，对GPS信号进行了仿真验证，其信号捕获的实现结构如图2所示。分别对高动态和弱信号两种条件下的伪码多普勒补偿性能进行仿真验证。采用GPS C/A码进行仿真验证，其码率为2.048 Mc/s，采样速率为10 MHz。

3.1 高动态条件下的损耗分析

下面对存在码多普勒补偿和无码多普勒补偿两种情况下的捕获性能进行了仿真验证，其中相干积累时间为20 ms，仿真结果如图4和图5所示。这里采用伪码峰值损耗以及恒虚警概率下的检测概率来评估码多普勒对捕获性能的影响。

图4 采用可变分数阶延迟滤波器进行码多普勒补偿后的伪码峰值损耗

图5 不同载噪比条件下的检测性能

从图4及图5可以看出，本文提出的基于时延控制的码多普勒补偿方法是一种有效减轻码多普勒影响的解决方案。采用常数插值滤波的方式，即文献[10]给出的码多普勒补偿方式，峰值损耗可以降低至0.7 dB以下，捕获性能有了明显改善。并且，可以看出随着滤波器阶数的增大，由码多普勒造成的峰值损耗就越小，捕获性能改善得越明显。当采用三阶FARROW结构分数阶延迟滤波器时，峰值损耗可降低至0.3 dB以下。如果再提高滤波器阶数，峰值损耗降低就很小了。所以，在实际应用中取3阶延迟滤波器是比较好的一个选择。

3.2 弱信号条件下的损耗分析

和高动态条件下一样，下面对弱信号条件下存在码多普勒补偿和无码多普勒补偿两种情况下的捕获性能进行了仿真验证。

图6给出了进行码多普勒补偿后的伪码峰值损耗随中频积累时间的关系图，可以很明显地看出，本文提出的基于时延控制的码多普勒补偿方法是一种有效减轻弱信号条件下码多普勒影响的解决方案。采用常数插值滤波的方式峰值损耗和高动态条件下一样可以降低至0.7 dB以下。并且，随着滤波器阶数的增大，由码多普勒造成的峰值损耗就越小，当采用三阶FARROW结构分数阶延迟滤波器时，峰值损耗同样可降低至0.3 dB以下。同时图7给出了中频积累时间为100 ms时进行码多普勒补偿后的捕获性能，可以看出，进行伪码多普勒补偿后，检测性能得到了比较明显的提升。

图6 采用可变分数阶延迟滤波器进行码多普勒补偿后的伪码峰值损耗

图7 不同载噪比条件下的检测性能

4 结束语

本文提出了一种基于时延控制的伪码多普勒补偿方法，并给出了包括码多普勒补偿在内的新的GNSS信号捕获结构。通过延迟滤波器调整由本地PN码和接收信号之间的不匹配所造成的时延值实现码多普勒的补偿。对延迟滤波器的设计提出了一种简单可行的方案。最后，对提出的码多普勒补偿方法的性能进行了仿真验证。本文提出的码多普勒补偿方法实现简单，而且不影响传统导航信号的捕获结构，为高动态和高灵敏度接收条件下的码多普勒补偿提供了一个有效的解决方案。

[1]Heque J，Erturk M C，Arslan H.Aeronautical ICI analysis and Doppler estimation[J].IEEE Communication Letters，2011，15（9）：906-908.

[2]Kaplan E D，Hegarty C J.Understanding GPS：principles and applications[M].2nd ed.Boston：Artech House Inc.，2006：58-61.

[3]Bao-Yen Tsui J.Fundamentals of global positioning system receivers：a software approach[M].New York：John Wiley&Sons，Inc.，2000：137-138.

[4]Akopain D.Fast FFT based GPS satellite acquisition method[J].IEE Proc Radar Sonar Navigation，2005，154：277-286.

[5]黄仰博.高性能导航接收机基带处理算法与实现技术研究[D].长沙：国防科学技术大学，2011.

[6]李春霞.高动态条件下伪码相关特性及其应用研究[D].长沙：国防科学技术大学，2005.

[7]Laakso T I，Välimäki V，Karjalainen M，et al.Splitting the unit delay—tools for fractional delay filter design[J].IEEE Signal Processing Mag，1996，13（1）：30-60.

[8]Shyu J J，Pei S C.A generalized approach to the design of variable fractional delay FIR digital filters[J].Signal Process，2008，88：1428-1435.

[9]Vesma J，Saramäki T.Optimization and efficient implementation of FIR filters with adjustable fractional delay[C]//Proc IEEE Int Symp Circuits Systems，Hong Kong，1997，4：2256-2259.

[10]Dafesh P A，Holmes J K.Practical and theoretical tradeoffs of active parallel correlator and passive matched filter acquisition implementations[C]//Proc IAIN World Congress，ION 56th Annual Meeting，San Diego，USA，2000：352-362.

[11]Tseng C C，Lee S L.Design of fractional delay filter using weighted Hermite interpolation method[J].IEEE Trans on Circuits Syst I：Reg Papers，2012，59：1458-1471.