大数据下不完备信息系统近似空间的并行算法

姜 麟，米允龙，王 添

JIANG Lin,MI Yunlong,WANG Tian

昆明理工大学 理学院，昆明 650500

Faculty of Science,Kunming University of Science and Technology,Kunming 650500,China

1 引言

随着大数据时代的来临，对海量数据进行挖掘已成为研究的热点。而大数据不只是海量的数据，拥有了海量数据后，并且有能力进行处理和分析，挖掘出数据的价值才可以获取数据的价值，从中获取真知[1]。面对如何挖掘出海量数据的价值，Google公司提出了分布式文件系统GFS（Google File System）[2]和MapReduce并行编程模式[3]，这为数据挖掘提供了一个很好的平台。在此基础上，已有不少学者致力于相关研究，并取得了一定的效果。例如，文献[4]提出的基于MapReduce的Web日志挖掘，文献[5]对在MapReduce框架下的分布式近邻传播聚类算法的研究等。

对于海量数据，传统的精确处理不再适用[1]，更多的是近似性处理。粗糙集理论是一种新的处理模糊和不确定性知识的数学工具，目前成功应用于机器学习、决策分析、模式认别和数据挖掘等领域[6]。基于粗糙集理论，目前已提出许多处理海量数据的算法。如文献[7]对海量数据的粗糙集近似空间并行算法的研究，文献[8-11]提出的各种处理海量数据的并行知识约简算法。然而，以上都是基于未带缺失信息的海量数据，在实际应用中，很多数据是带有缺失信息的[12-13]。对于不完备的信息系统或带缺失信息的海量数据，往往可以采用集值信息系统来处理[13]。同时，传统的算法是假设所有数据一次性装入到内存中去，但这并不适用于海量数据。因此，对带缺失信息的海量数据进行研究是十分必要的。探讨如何基于MapReduce并行编程框架，实现对不完备信息系统的上、下近似的并行算法研究，对带缺失信息的海量数据进一步挖掘具有重要的促进作用。

通过深度分析不完备信息系统的特征，本文在第二部分结合MapReduce并行编程的特点，给出了对原有集值信息系统进行扩展的相关理论。在第三部分提出了一种基于MapReduce框架下不完备信息系统近似空间的并行算法。第四部分通过实验结果表明，该并行算法对处理带缺失信息的海量数据是可行的，高效的。

2 相关理论

在这一部分，将介绍一下MapReduce相关技术[2-3]、不完备信息系统[6-7，12，14-16]及其扩展相关理论。

2.1 MapReduce并行编程模型

MapReduce模型是Dean和Ghemawat于2008年提出的并行编程模式，描述如下[3]：

首先，接收输入key-value对集合；再而，通过执行Map和Reduce两个函数；最后，输出相应的key-value对集合。因此，只需要设计出相应的Map和Reduce函数，就能将任务进行并行计算，其形式如下：

Map函数接收一组输入键值对(k1，v1)，键值对(k1，v1)经过Map函数处理后，并按k1进行排序；combiner类把相同键k1关联的值v1进行本地聚类，产生中间键值对(k2，v2)；在Reduce阶段，键k2相同数据的将会被送到同一个Reducer任务中，Reduce再把相同键k2的数据整合在一起，进行处理。

2.2 粗糙集相关概念

信息系统 S=(U，AT，V，f)，U=(x1，x2，…，xn)是对象的非空有限集合，称为论域；AT是属性的非空有限集合；特别的，如果AT=U∪D，C为条件属性的非空有限集，D为决策属性的非空有限集，且C∩D=∅，则称S为决策信息系统。其中V=∪a∈ATVa，Va是a属性的值域；f:U×AT→V是一个信息函数，它为每一个对象的每个属性赋予一个信息值，即∀a∈AT，x∈U，则有f(x，a)∈Va。

定义1[12]对于信息系统S=(U，AT，V，f)，若至少有一个属性a∈AT使得Va中含有缺省值（记作*），则称S是一个不完备信息系统，记为IS。若AT=C∪D，且有C∩D=∅，则不完信息系统IS称为不完备决策系统（或不完备决策表），记为DS。

定义2[14-15]设 IS=(U，AT，V，f)是一个不完备信息系统，如果 ∀a∈AT，x∈U，若有 f(x，a)=*，令 f(x，a)=Va，则称这是一个不完备信息系统向集值系统的一种转换，为了简便起见，称转换后的信息系统仍为集值信息系统，记为SIS。SIS是集值信息系统，若AT=C∪D，且有C∩D=∅，则称集值信息系统为集值决策表，记为DIS。

定义3[16]设 DIS=(U，C，D，V，f)是集值决策表，对∀a∈A，x∈U，f(x，a)取值从语义方面被析取地解释。例如：a表示属性“语言能力”，则 f(x，a)={德语，法语，汉语}也可以解释对象x会说德语，法语和汉语其中的一种语言。

定义4[14-15]设 DIS=(U，C，D，V，f)是集值决策表，任意属性子集B⊆C，定义二元系：

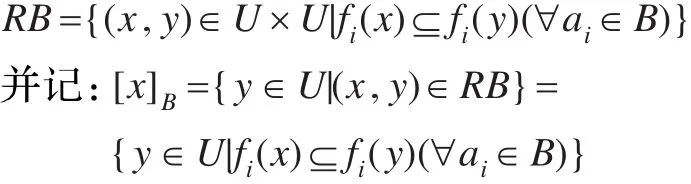
显然，RB是自反和传递的，未必是等价关系。

定义5[15]设 DIS=(U，C，D，V，f)是集值决策表，对于任意 X⊆U，记：

定义6 设 DIS=(U，C，D，V，f)是集值决策表，若对∀x∈U，∀a∈C ，若有 f(x，a)=Va，则取 f(x，a)=ai，其中ai∈Va，i表示Va中属性值的取值数，其中，x=x[1]∪x[2]∪…∪x[i]。则称为集值决策表 DIS的一个扩展，其中Uˉ=U∪x[i]。

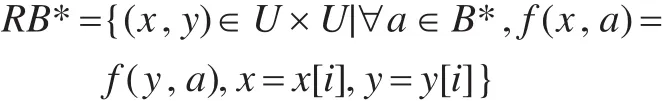
其中，[x]B*={y∈U|(x，y)∈RB*}。对于任意 X⊆U ，U/RB*={E1，E2，…，Em}，为了简便，记：U/B* 。

则定义相应的上近似和下近似如下：

例1表1为一个不完备决策信息系统，表中“*”表示缺省值。根据定义2和定义3，对不完备信息系统进行转换。如 f(x3，a1)=*，由定义2、定义3可得，f(x3，a1)={1，2}。其余进行同样的转换，则可得集值决策信息系统表2。

由定义4和定义5得到(B=C={a1，a2，a3，a4})：[x1]B={x1}，[x2]B={x2}，[x3]B={x3}，[x4]B={x3，x4}，[x5]B={x3，x5}，[x6]B={x6}。取 X={x1，x2，x3}，则实际上，x5，x6很可能被分在同一类，而在此却没有。可以看出，下近似比较宽松，而上近似比较严格。为了解决这种情况和大数据的计算要求，对集值信息系统按定义6进行扩展，如表3。

表1 一个不完备决策信息系统

表2 一个集值决策信息系统

表3 决策信息系统

表3 决策信息系统

x1 x2 x3[1]x3[2]x3[3]x3[4]x4[1]x4[2]x5[1]x5[2]x6[1]x6[2]a1111122111222 a2121212121112 a3211111111111 a4221111111112 D112222111122

由定义7可得（其中 B*=C={a1，a2，a3，a4}）：[x1]B*={x1}，[x2]B*={x2}，[x3]B*={x3，x4，x5，x6}，[x4]B*={x3，x4，x5}，[x5]B*={x3，x4，x5，x6}，[x6]B*={x3，x5，x6}。取 X={x1，x2，x3}，则有上、下近似为：x4，x5，x6} 。

3 基于MapReduce的不完备信息系统近似空间的计算

在这部分，将根据第二部分的相关理论，研究在MapReduce框架下不完备信息系统近似空间的并行算法。

3.1 MapReduce框架下近似空间算法的并行性研究

于是，关于B*的二元关系定义如下：

则关于 B* 的划分 U/B*={E1，E2，…，Em}，对任意E∈U/B*={E1，E2，…，Em}可以定义如下：

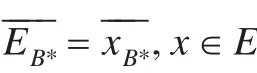
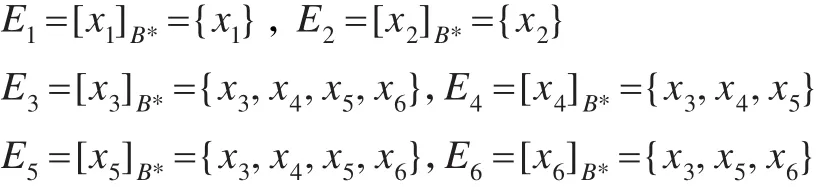
对于信息集合E1，有如下：

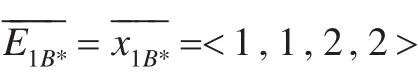
例3 D为决策属性，根据定义8、9可得，U/D={D1，D2}，其中 D1={x1，x2，x4，x5}，D2={x3，x6}。则有：

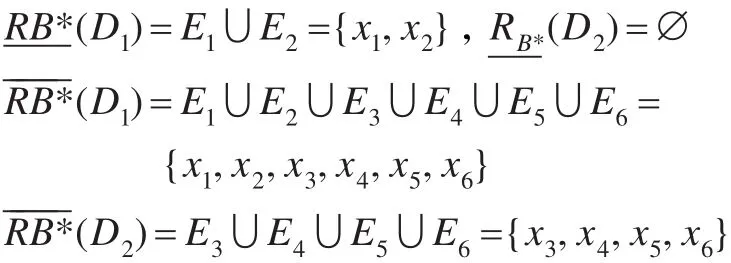
根据定义10可得，不完备信息系统经过转换成集值信息系统，并进行扩展后，可以将其划分成n个子集值决策信息系统。这说明并行编程的可行性。

3.2 基于MapReduce框架下的并行算法

3.2.1 基于MapReduce下不完备信息系统的二元关系B*的划分类U/B*计算

算法1 Map（）与Reduce（）函数

算法1是在MapReduce框架下把不完备信息系统转化成集值信息系统，并求出相应二元关系划分类。此算法除Map（）和Rduce（）函数外，还有对不完备信息进行集值化的splitMap（）递归函数。

3.2.2 基于MapReduce下不完备决策信息系统决策类的计算

算法2 Map（）与Reduce（）函数

算法2是根据决策属性来划分决策关系类，把决策属性相同的对象划分到同一类中。

3.2.3 不完备信息系统近似空间的并行计算

算法3 上近似Map（）与Reduce（）函数

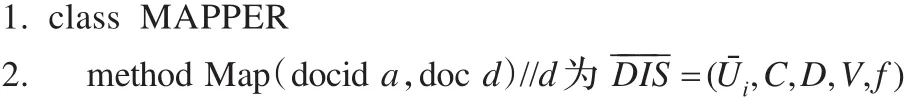
算法3是处理上近似并行算法，此处存储的是上近似的索引值，以防止内存溢出。下面算法4关于下近似并行算法存储的也是索引值。

算法4 下近似Map（）与Reduce（）函数

4 实验结果及分析

4.1 数据集及实验环境描述

在这部分，将选用UCI机器学习数据库（http：//archive.ics.uci.edu/ml/datasets.html）中带缺失信息的两个数据集Mammographic Mass Data Set和Breast Cancer Wisconsin Data Set；为了简便，分别记为：MMDS、BCDS。现在，将MMDS分别复制800次和8 000次，得到新的数据集记为：MMDS1、MMDS2；将BCDS分别复制8 000次和80 000次，得到新的数据集记为：BCDS1、BCDS2。具体数据集描述如表4所示。

表4 数据集的描述

本实验环境采用Hadoop集群（http：//hadoop.apache.org/），该集群由1台主控制节点和8个计算节点构成。每个节点配置为Intel®Pentium®D CPU 2.80 GHz，2 GB内存和150 GB硬盘。操作系统为Linux Centos 6.3，JDK为Java 1.7.0_17，Eclipse采用32位的Linux版本eclipse-3.3.2。MapReduce框架基于Hadoop平台0.20.2，其他采用系统默认设置。

4.2 算法效果及验证

此节，将主要从加速比（speedup）、可扩展性（scaleup）[17]和运行时间3个方面对并行算法进行评价及验证。

（1）运行时间

数据集 MMDS1，BCDS1，MMDS2，BCDS2分别在1～8个计算节点运行，运行结果如表5所示。

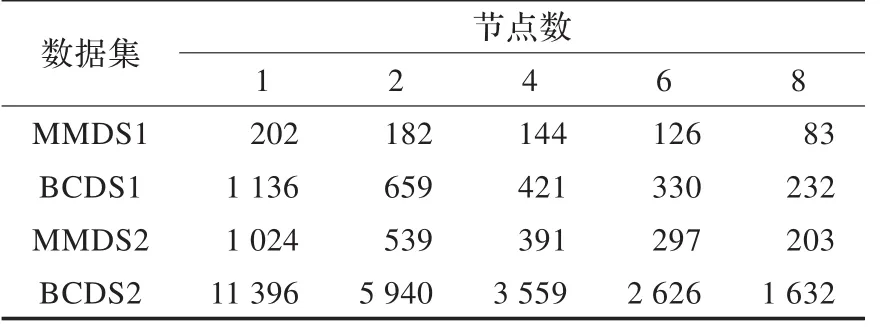
表5 并行算法的运行时间 s

如表5所示，同一数据集随节点数增加而运行时间不断减少。并且，数据量越大，递减的效果越好。这表明，对于大数据，基于MapReduce并行编程取得很好效果。表5还显示出，虽然数据集BCDS1记录数比数据集MMDS2少，但是其属性项数比数据集MMDS2多，导致其运行时间比数据集MMDS2长。易得出，属性集在上、下近似算法是至关重要的。

以下给出与计算节点数成比例增长的数据集的运行时间。为了计算方便，取记录数为100 000的数据集MMDS1于一个计算节点上运行，仍记为：MMDS1。同样，BCDS1，MMDS2，BCDS2在一个计算节点上运行的数据量分别为：700 000，1 000 000，7 000 000。

具体如对于数据集BCDS1来讲，用700 000记录数在一个计算节点上运行，则用700 000×2记录数在两个计算节点上运行，并依次下去，可得运行时间如表6所示。

（2）加速比（speedup）

为了测试加速比，固定数据集规模，不断增加数据的计算节点数。通常，线性加速比是十分理想的；但是，由于节点数增加，集群之间的通信时间会不断增加。因此，一般很难达到理想的线性加速比。公式如下[17]：

表6 并行算法可扩展性的运行时间 s

其中，T1是固定规模数据集在一个节点上运行时间，Tm是同样固定规模数据集在m个节点运行时间。

根据表5提供的并行算法运行时间，运用加速比公式（1），可得图1。

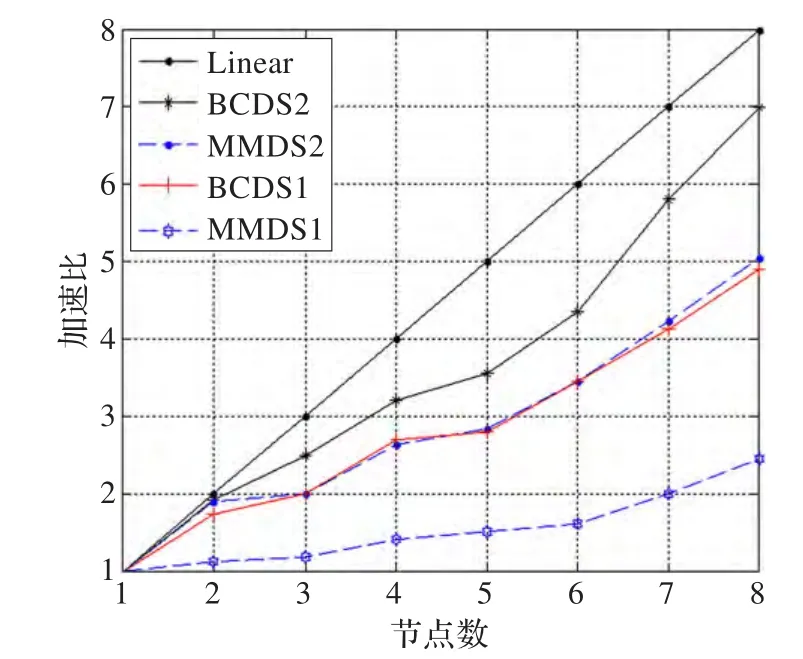
图1 加速比

如图1所示，不同数据集随着计算节点数增加的加速比趋势。从图可以看出，数据集的记录数越多加速比越好，如数据集BCDS2与数据集MMDS1相比，其加速比要好。因此，对于带缺失信息的海量数据集，基于MapReuce编程模型的并行算法有效性得到证实。

（3）可扩展性（scaleup）

可扩展性指的是同计算节点数成比例增长的数据集的性能比，公式如下[17]：

其中，TDB1是数据集DB在一个计算节点上运行时间，TDBm是数据集m×DB在m个计算节点上运行时间。根据表6提供的并行算法可扩展性的运行时间，运用可扩展性公式（2），可得图2。

如图2所示，各数据集随着计算节点数增加的可扩展性趋势。从图2可以看出，各数据集都有较好的可扩展性。同时，图2还显示出，数据集规模越大，可扩展性越好，越趋于稳定。

5 结束语

图2 可扩展性

随着数据的重要性和不确定性增加，粗糙集已经成为数据挖掘的一种有效工具。运用粗糙集进行数据处理时，上、下近似是其必要的步骤。然而，传统的上、下近似算法不适合处理海量数据，更不适合对带缺失信息的海量数据进行挖掘。为了促进对带缺失信息的海量数据研究，提出了MapReduce框架下不完备信息系统的一种近似空间并行算法。通过对并行算法的时间、加速性和可扩展性的实验，表明对缺失信息不是很多的情况下，该算法是高效的，能够处理带缺失信息的大规模数据集。这对进一步研究带缺失信息的海量数据具有重要的参考价值。

[1]怀进鹏.大数据及大数据的科学与技术问题[C/OL]//第五届中国云计算大会，北京，2013.http：//www.ciecloud.org/2013/index.html.

[2]Ghemawat S，Gobioff H，Leung S T.The google file system[C]//SOSP’03，2003：29-43.

[3]Dean J，Ghemawat S.MapReduce：simplified data processing on large clusters[J].Communications of the ACM，2008，51（1）：107-113.

[4]李彬，刘莉莉.基于MapReduce的Web日志挖掘[J].计算机工程与应用，2012，48（22）：95-98.

[5]鲁伟明，杜晨阳，魏宝刚，等.基于MapReduce的分布式近邻传播聚类算法[J].计算机研究与发展，2012，49（8）：1762-1772.

[6]张文修，吴伟志，梁吉业，等.粗糙集理论与方法[M].北京：科学出版社，2001.

[7]Zhang Junbo，Li Tianrui.A parallel method for computing rough set approximations[J].Information Sciences，2012，194（1）：209-223.

[8]Yang Y，Chen Z，Liang Z，et al.Attribute reduction for massive data based on rough set theory and MapReduce[C]//Yu J.The Fifth International Conference on Rough Set and Knowledge Technology.Berlin Heidelberg：Springer-Verlag，2010：672-678.

[9]钱进，苗夺谦，张泽华.云计算环境下知识约简算法[J].计算机学报，2011，34（12）：2332-2343.

[10]钱进，苗夺谦，张泽华.云计算环境下差别矩阵知识约简算法研究[J].计算机科学，2011，38（8）：193-196.

[11]钱进，苗夺谦，张泽华，等.MapReduce框架下并行知识约简算法模型研究[J].计算机科学与探索，2013，7（1）：35-45.

[12]Kryszkiewicz M.Rough set approach to incomplete information systems[J].Information Sciences，1998，112（1）：39-49.

[13]张文修，梁怡，吴伟志.信息系统与知识发现[M].北京：科学出版社，2003.

[14]宋笑雪，李鸿儒，张文修.集值决策信息系统的知识约简与属性特征[J].计算机科学，2006，33（7）：179-181.

[15]宋笑雪，李鸿儒，张文修.集值信息系统的知识约简与属性特征[J].计算机工程，2006，32（22）：26-36.

[16]Qian Y，Dang C，Liang J，et al.Set-valued ordered information systems[J].Information Sciences，2009，179（16）：2809-2832.

[17]Xu Xiaowei，Jager J，Kriegel H P.A fast parallel clustering algorithm for large spatial databases[J].Data Mining and Knowledge Discovery，1999，3（3）：263-290.