利用分布式狼群算法进行三维传感器优化布置的方法研究

伊廷华， 王传伟， 李宏男

(大连理工大学建设工程学部土木工程学院， 辽宁 大连 116023)

引 言

交通运输关系国计民生和经济命脉，而大跨桥梁则是公路和铁路连接的关键结点。为了确保大跨桥梁的服役安全，对其在施工及服役期间进行健康监测与安全性评估是十分必要的。为了实现该目的，首先需要获取结构的重要响应，而这些响应数据需要由合理布设在结构上的传感器来测得，考虑传感器本身需要一定的成本，与其配套使用的数据采集和处理设备的造价也都较高，从经济方面考虑，希望采用尽可能少的传感器来达到监测的目的，因此传感器位置和数量优化的问题应运而生。一种好的传感器布设方案应满足[1]：1) 在含噪音的环境中，能够利用尽可能少的传感器获取全面而精确的结构响应信息；2) 测得的结构响应信息应能够与数值分析的结果相对应；3) 对感兴趣的振动响应数据能够进行重点采集；4) 监测结果具有良好的可视性和鲁棒性；5) 监测系统的设备投入、数据传输和结果处理的费用能够最少。

传感器优化布置属于组合优化问题，同时也是多维优化问题。以往算法只能针对结构的某一方向进行传感器的优化布置，如果将多维传感器布置在这些测点上，会造成传感器在优化的结构振动方向最优，而在其余方向不是最优。针对此问题，各国学者已开展了一些初步的研究，如Kammer和Tinker在有效独立法的基础上[2]，提出了一种将三维加速度传感器作为独立单位进行优化布置的方法，并以X-33航天器为例，与其他方法进行对比验证；江祥林和程高以有效独立法为准则[3]，开发了三维加速度传感器优化布置MATLAB工具箱，并计算给出了九江长江大桥的三维传感器优化布置方案，模态试验结果验证了该布置方案的合理性。采用传统的传感器布置方法有其简单、实用的优点，但这些方法得到的结果却往往是次优的，即通过此类方法所得到的传感器布置位置无法保证理论与实测信息之间的误差最小。近些年，一些新型智能优化算法如粒子群算法、遗传算法、蚁群算法和猴群算法等的出现，因其具有较好的寻优能力而取得了较快的发展。一些研究已表明，将智能算法与优化准则相结合，可取得更好的优化效果。He等提出了一种Moran′s I法[4]，解决了多维传感器布置信息冗余问题，以黄河上游的拉西瓦拱坝为例，通过改进的粒子群算法对其进行优化计算，验证了该方法的有效性和算法的高效性；刘宇等给出了基于遗传算法的加速度传感器布置的实施过程[5]，并以润杨大桥斜拉桥为例，对比分析了多目标函数优化布置方法与单目标函数方法相比的优越性；Fidanova等提出无线传感器网络布置问题[6]，以传感器数量为目标函数，利用蚁群算法进行优化布置，结果表明：蚁群算法的搜索结果优于进化算法。伊廷华等提出改进猴群算法的传感器优化布置方法[7]，以大连世贸大厦为例，证明了该算法较经典序列法有较大的优越性。

本文建立了一种传感器的三维模态置信准则，基于新型智能算法——狼群算法(Wolf algorithm，简称WA)[8]，提出了一种分布式狼群算法(Distributed wolf algorithm，简称DWA)，通过在狼群中引入分组的策略，大幅提高了算法的并行搜索效率，文末通过一个基准模型验证了该方法的可行性和有效性。

1 三维优化准则的建立

1.1 理论基础

众所周知，Fisher信息阵(Fisher information matrix，简称FIM)等价于待估参数估计误差的最小协方差矩阵，其能够度量测试响应中所包含信息的多少，表达式为

F=ΦTΦ

(1)

式中F为Fisher信息阵；Φ为模态振型矩阵；ΦT为Φ的转置。

根据文献[2]，F可以表示为各个自由度贡献之和，即

(2)

式中F为全部自由度的FIM；Fk为第k个自由度的FIM；φk,*为Φ的第k行；nc为结构的自由度个数。

结构的每个节点包括三个平动和三个转动自由度，由于转动自由度在实际测试中较难直接测到，因此这里只考虑三个平动自由度的优化布置。将节点在x,y,z三个方向上的模态向量作为一个单元，此时FIM可表示为

(3)

式中F为全部节点的FIM；F3k为第k个节点的FIM；φ3k,*为Φ中第k个节点的三个平动自由度所对应的模态向量组成的矩阵；n为节点数目。

模态置信准则(Modal assurance criterion，简称MAC)是判断结构的实测模态向量间是否相互线性独立的基本要求[9]，其表达式为

(4)

式中φ*,i和φ*,j分别为振型矩阵Φ中的第i列和第j列。

1.2 三维优化准则

借鉴式(3)以节点为单位的方法，可得到待布置传感器的Fisher信息阵Q

(5)

式中Q3k为第k个三维传感器位置所对应节点的FIM；φ3k,*为Φ中第k个节点的三个平动自由度所对应的模态向量组成的矩阵；nsp为待布置的三维传感器数量。

因此，可以借鉴MAC的方法来衡量Q的优劣，进而建立起三维模态置信准则(Triaxial modal assurance criterion，简称TMAC)，即

(6)

式中Qi,j为待布置传感器的FIM的第i行第j列元素；TMACi,j为TMAC中第i行第j列元素，且TMACi,j∈[0,1]。

TMAC矩阵非对角元的值越小，各阶测试节点振型的独立性越好，线性相关性越小，传感器的布设效果也就越好；反之，传感器布设效果越差。因此，可以以TMAC非对角元元素的最大值的最小化为三维传感器的优化目标，即本文提出的三维优化准则可写为

min(f)

(7)

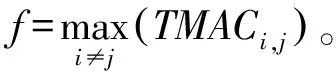
2 基于分布式狼群算法的三维传感器优化布置方法

WA由鄢小虎和柳长安于2010年提出的一种模拟狼群捕食的群智能优化算法[8]，主要用于解决带有连续变量的全局优化问题，其基本思想是模拟狼群捕食的三个过程，即游猎、围攻和食物分配。其中：游猎过程主要是狼个体依据自身的力量搜索当前所在位置附近的局部最优值；围攻过程是狼群利用群体中最优狼个体的信息搜索全局最优值；食物分配过程通过随机产生新个体取代目标函数值差的狼个体，以避免算法陷入局部最优。与传统优化算法相比，WA的优点主要包括：1) 不要求目标函数连续或可微，对于线性或非线性的问题均可求解；2) 算法的实现过程较为简单，且能够以较快速度搜索到高维数优化问题的最优解或次优解。由于WA只适用于连续变量问题的求解，若将其用于传感器优化布置，需要对其编码方式进行改进。此外，通过计算可以发现狼群在围攻的过程中，由于狼群中的每只狼个体都向猎物逼近，这会极大地降低狼群的多样性，使得算法在迭代过程中易陷入局部最优。为此，本文建立了一种分布式狼群算法，将狼群分为多个组，通过限制组内参与围攻的狼个体数量，仅采用组内最差个体向最优个体逼近的搜索机制，既避免了狼群多样性的降低，又使得组内的信息能够充分共享，大幅提高算法的求解效率。

2.1 狼群的编码及其初始化

对欲布置传感器的结构建立有限元模型，通过模态分析，获取结构的振型矩阵，并对传感器的候选布置位置进行编号。所有节点位置即为传感器的候选优化位置。考虑传感器优化布置的特点，这里引入双重编码方式进行解的表达[10]，即利用有序对(x,s)来表示狼群的个体，来对应传感器布置问题的可行解。其中，x为位置向量，即在搜索过程中是以此向量进行迭代搜索的；s为二进制向量，即表示传感器的布置位置。狼群编码及初始化的步骤如下：

步骤 1：假设所有节点的数目为n，对其进行编号，即1～n。

步骤 2：以狼群中第i只狼个体为例(i=1,2,…,P，P为狼群个体数目)，其相应的解可表示为：pi=(xi,si)={(xi,1,si,1),(xi,2,si,2),…,(xi,n,si,n)}。位置向量xi为从区间[xdown,xup]之间随机产生的实数数组，其各维分量可按下式产生

xi,j=rand×(xup-xdown)+xdown

(8)

式中rand为[0,1]内的随机数。

si,j为xi,j通过下式中的函数转换而得到二进制编码向量

(9)

采用式(9)时，需要首先设定一个判断阈值ε和区间[xdown,xup]，若sig(xi,j)>ε，则该分量si,j取1，即表示在该节点的位置处布置传感器；若sig(xi,j)≤ε，则该分量取0，即代表在该节点位置上不布置传感器。通过试算可以发现，当xi,j在[-5,5]之间取值时，0.006 7≤sig(xi,j)≤0.993 3，可见取值是合理的，因此本文取xdown=-5，xup=5。

对于初始化产生的解，si中传感器的布置数目可能会出现不等于nsp的情况，即不满足编码要求，则此时应重新进行初始化，重复步骤2直到初始化的解满足编码的要求为止，本文后面的各个过程遇到类似情况均做同样处理。

因为狼个体的初始化是随机的，而产生的有效狼个体需要满足编码要求，这就意味着产生的狼个体并不都是有效的。为了提高有效狼个体的产生效率，这里提出一种基于概率法判定阈值ε的方法。以狼个体pi的第j维分量pi,j为例，使si,j取值为1的概率为nsp/n，而si,j取值为0的概率为1-nsp/n，这样即可保证产生的狼个体在统计上能够满足编码要求。若xi,j∈[xdown,-xseta]，则si,j=0，对应si,j取值为0的概率为1-nsp/n；若xi,j∈(-xseta,xup]，则si,j=1，对应si,j取值为1的概率为nsp/n。因此，xseta的取值为

xseta=(nsp/n)×(|xdown|+|xup|)-|xup|

(10)

即区间[xdown,xup]以-xseta为界进行分割，因此ε的适宜取值为1/(1+exseta)。ε的这种取值方式不但能够加快有效初始狼群的产生速度，而且能够保证狼群个体各维分量的均匀性。

2.2 狼群分组

原WA仅通过单个狼群进行搜索，这对于解决多自由度优化的问题时，全局搜索能力不强，耗费时间也较长。基于此，本文提出通过设定多个狼群进行同步并行搜索的方法，即将初始化狼群个体以一定的方式将其分配到多个组内，然后进行同步并行迭代计算，较好地解决了这一问题。

设初始产生的狼群的个体数为P，将其分为M个组，每个组内有N只狼个体。这里将每个组内目标函数值最优的狼个体记为头狼。狼群分组的步骤如下：

步骤1：狼群中狼个体目标函数的求解。设第i只狼个体位置向量为xi，利用其相应的二进制向量si，得到布置传感器的节点编号，代入式(5)计算Q，然后把Q代入式(6)计算TMAC，最后把TMAC代入目标函数，即得到其值f(pi)。

步骤 2：将狼群中狼个体按目标函数值由差到优进行排序，然后把第1只狼个体放入第1组，第2只狼个体放入第2组，…，第N只狼个体放入第N组，第N+1只狼个体放入第1组，第N+2只狼个体放入第2组，依次重复直到P只狼个体分配完毕。

2.3 游猎行为

分组后每个组内的狼个体都参与游猎找寻猎物。狼个体在每走一步之前，先计算向周围h个方向前进一步的位置，然后找到h个位置中的最优位置da，若da比当前位置优，则该狼个体向前移动到位置da,并以da为当前位置继续向前搜索；若找不到更优的位置，则该狼个体的游猎行为结束。狼个体的游猎方程可表示为

yc,j=xi,j+(2×rand-1)×stepa

(11)

式中rand为[0,1]内的随机数；stepa为搜索步长；xi,j为第i只狼个体的第j维分量(j=1,2,…,n)，yc,j为xi,j周围第c(c=1,2,…,h)个位置的第j维分量。

设狼群经上述分组后，以第m(m=1,2,…,M)个组第l只狼个体位置向量xe为例，游猎步骤如下：

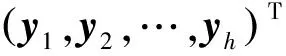
步骤2：计算各个yc的目标函数值，若这h个新位置中最优的位置比之前的位置优，则将狼个体的位置向量变为此向量；反之，狼个体位置保持不动。

步骤3：重复步骤1和步骤2直到设定的搜索次数Nh。

2.4 围攻行为

Δx(w,j)d=rand×stepb×(x(best,j)d-x(worst,j)d)，

(Δxmin≤Δx(w,j)d≤Δxmax)

(12)

式中stepb为狼个体围攻猎物的步长；x(best,j)d为第d次迭代中头狼第j维分量(j=1,2,…,n)，x(worst,j)d为第d次迭代中目标函数值最差的狼个体第j维分量。Δx(w,j)d为第d次迭代中目标函数值最差的狼个体第j维分量的围攻距离，为防止狼群在围攻过程中因围攻距离过大而容易错过全局最优值，采用阈值Δxmin和Δxmax来限制狼个体的围攻距离，即若Δx(w,j)d>Δxmax，取Δx(w,j)d=Δxmax；若Δx(w,j)d<Δxmin，取Δx(w,j)d=Δxmin。

x(worst,j)d+1=x(worst,j)d+Δx(w,j)d

(13)

式中x(worst,j)d和x(worst,j)d+1为围攻前和围攻后的组内最差狼个体的第j维分量。

围攻步骤如下：

步骤 1：游猎完成后，对狼群重新分组。通过分组可保证狼群组内的头狼位置的优越性。

步骤 2：以第m个组为例，通过组内目标函数值最差的狼个体xworst和组内目标函数值最优的狼个体xbest，利用式(12)和(13)更新最差狼个体的位置，得到更新后的狼个体。

2.5 食物分配原则

狼群的食物分配原则为先强后弱，即狼群捕捉到的大部分猎物会被强壮的狼占有，弱小的狼分配到的食物很少，尽管这种方式可能会饿死一些弱小的狼，但能保证强壮的狼在下次能更好地扑捉到猎物，不至于使整个狼群饿死，提高了狼群的生存能力。

本文模拟狼群的这种食物分配行为，去除每组中较差的t只狼个体，同时随机产生t只新狼个体，这能够显著增加狼群的多样性。狼群的食物分配原则步骤为：

半个多世纪以来，科学大洋钻探已经证明了板块构造理论的正确，开创了古海洋学，并通过揭示深海生物圈中种类繁多、数量庞大的生命，重新定义了我们对地球生命的看法，而且还有更多的东西需要学习和探索。

步骤1：按照狼群分组的步骤将围攻行为完成后的狼群重新进行分组，使得淘汰的狼个体为群体内的最差的个体。

步骤 2：利用狼群数据初始化的步骤每组产生t只新的狼个体，并用这t只狼个体取代组内目标函数值最差的t只原有的狼个体。

关于狼群分组的说明：本文方法在狼群游猎、围攻和食物分配过程前均进行狼群分组，即多次采用分组的方式。这是由于狼群经过某一步搜索过程后，各个组会得到不同的结果，分组可将这些结果进行比较，然后分配到新的组内，保证每个组内个体的均衡性。这种方式大大增强了不同组内狼个体的信息交流，提高算法的寻找最优值的效率。

2.6 算法终止条件

狼群算法的运行需要一定的循环次数Nc，当达到循环次数时优化布置过程终止，整个计算过程可通过科学计算软件MATLAB实现。

3 工程算例

3.1 计算模型简介

为了评价结构健康监测中各种算法的优劣，美国中佛罗里达大学开发了一个桥梁基准模型(图1)，本文即采用这一基准模型进行传感器位置的优化研究。该模型共两跨，总长5.486 4 m，宽1.828 8 m。桥梁沿纵向的主梁将荷载转移到支撑上，侧向稳定性由横向每隔0.914 4 m的次梁提供。基准模型梁截面都相同，均采用S3×5.7型钢。采用SAP2000进行建模[11]，有限元模型的数据被导到MATLAB中，以供使用者运行分析。模型共有177个节点，182个单元，每个节点包含3个自由度，分别对应x,y,z三个方向的信息。提取模型的刚度矩阵和质量矩阵，通过模态分析可得到结构的前10阶模态振型矩阵Φ。

图1 基准模型实物图

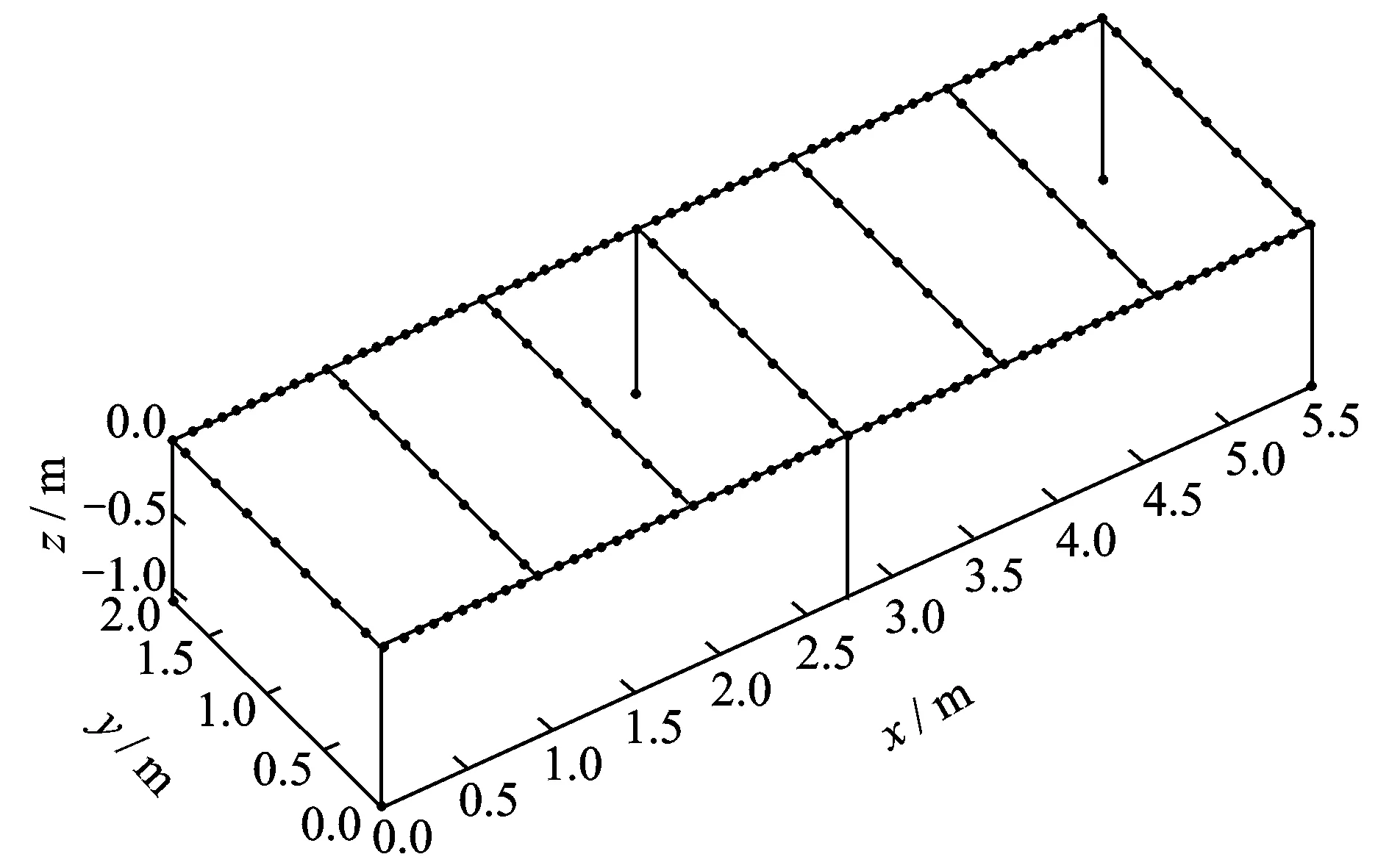
图2 基准模型的有限元模型

3.2 传感器优化布置

如图2所示，有限元模型的节点数为177，除去桥墩与地面接触部位没有平动自由度的6个节点，因此结构要考虑的节点数n=171。设需要布设的传感器数目nsp=20，传感器类型为三维加速度传感器。为了说明本文提出的DWA的优越性，同时采用另外两种方法进行对比研究，即：

工况1：原狼群算法，即WA；

工况2：分布式狼群算法，即DWA；

工况3：全节点三维传感器布置。

(1) 参数敏感性

优化算法中的参数取值会直接影响到算法的收敛性，因此在进行传感器优化布置之前，应对DWA进行参数敏感性分析，以便为选取合理的参数作参考。设狼群个体数目P=50，共分为M=5个组，这样每组内有N=10只狼个体，搜索区间上下限分别为xdown=-5和xup=5，围攻距离Δx的限定范围Δxmin=-0.5和Δxmax=0.5，算法的迭代次数Nc=200。这里选取影响DWA性能的4个重要参数进行分析：游猎搜索次数h×Nh，搜索步长stepa，围攻步长stepb，每组淘汰个数t。通过正交试验设计构成正交试验表L9(34)，分别表示：试验1～9号；4个因素t，stepa，stepb，h×Nh；每个因素有1，2，3三个水平，每个水平的取值如表1括号内的数值。每组试验独立运行5次，取其计算值的最优值，如表1所示。

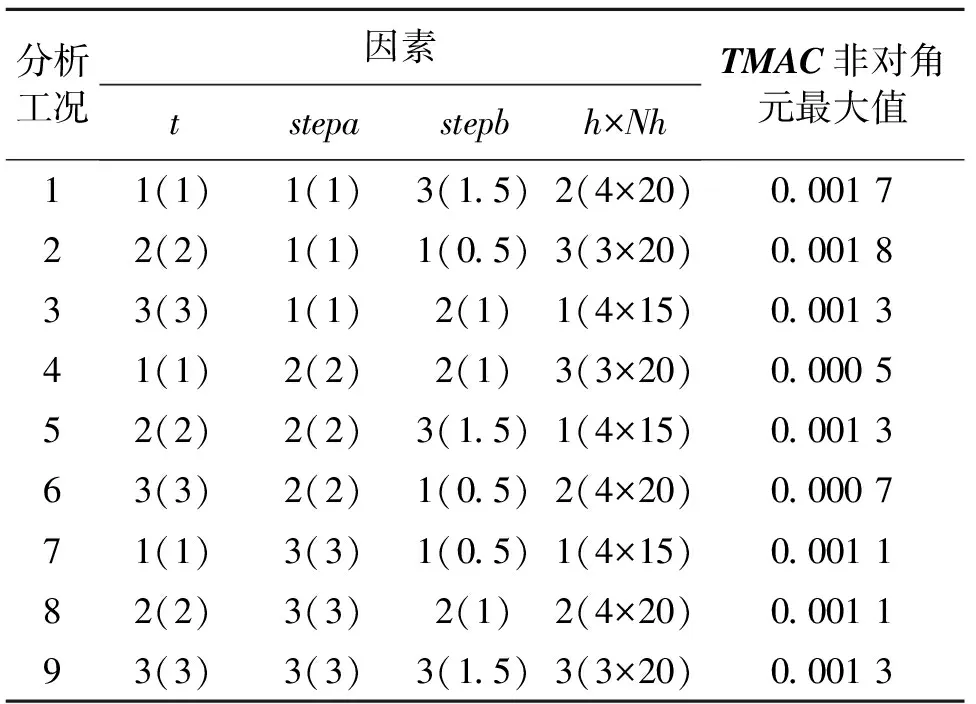
表1 正交试验表及试验结果

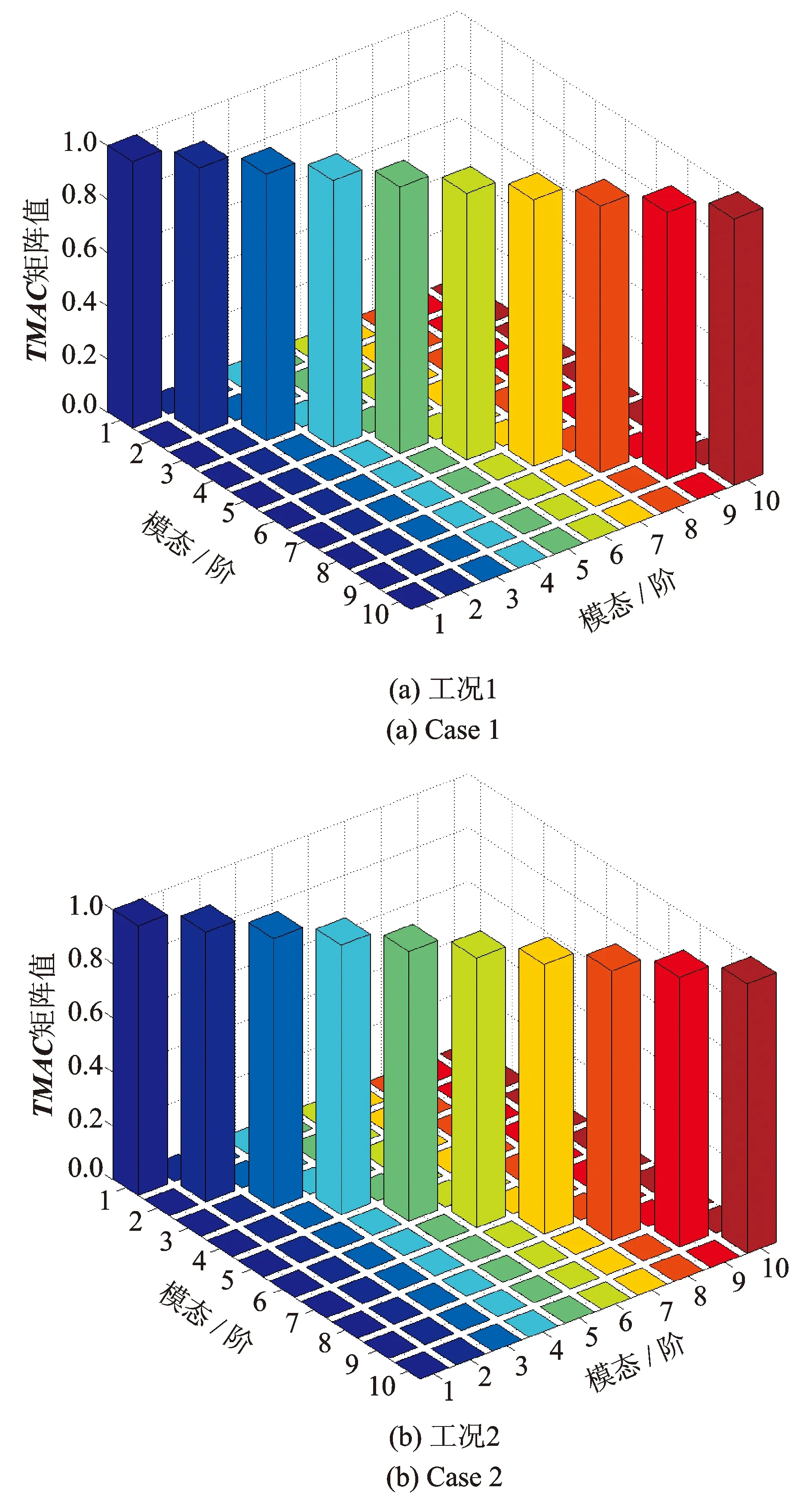
图3 由工况1和工况2得到的TMAC柱状图

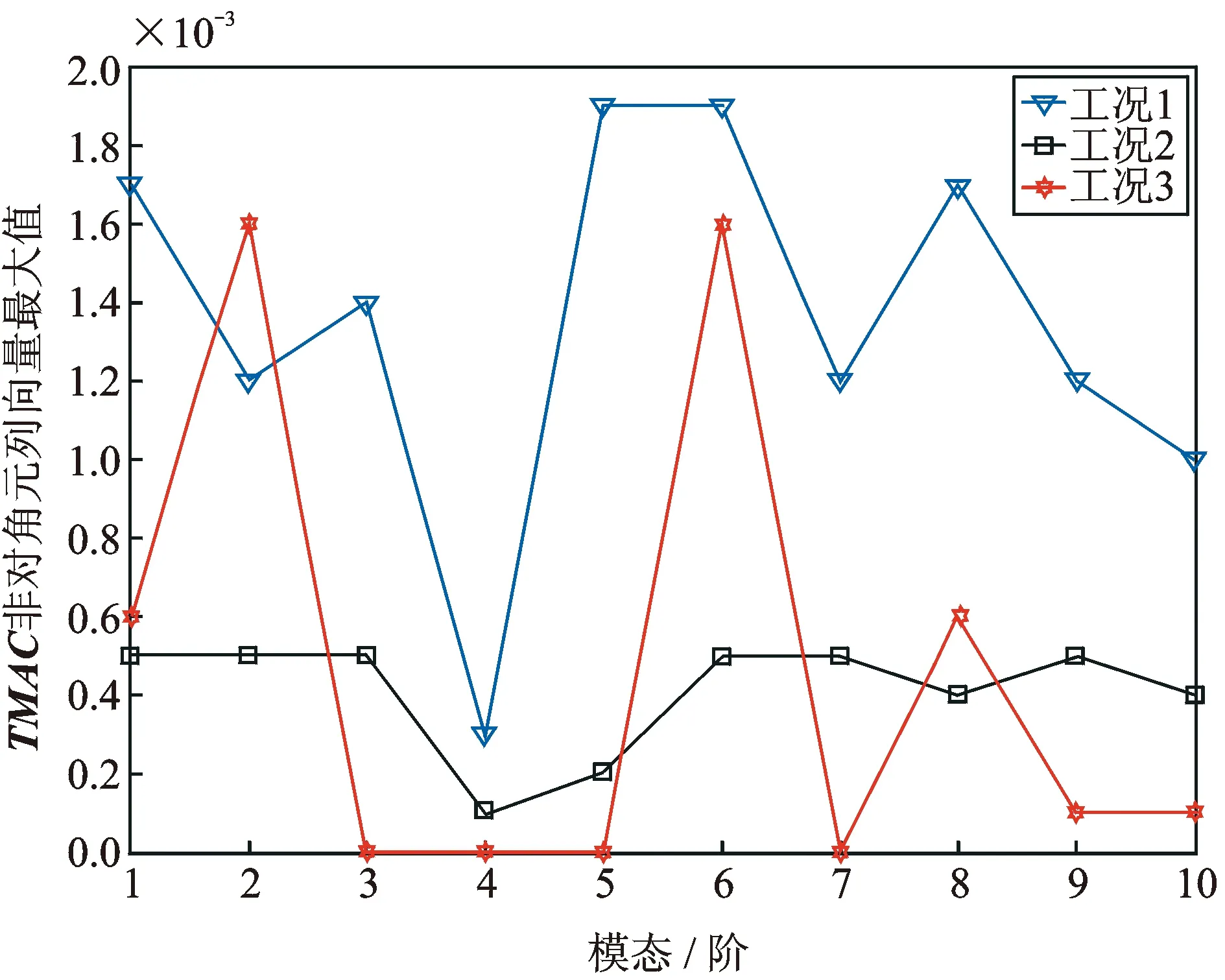
图4 TMAC非对角元列向量最大值

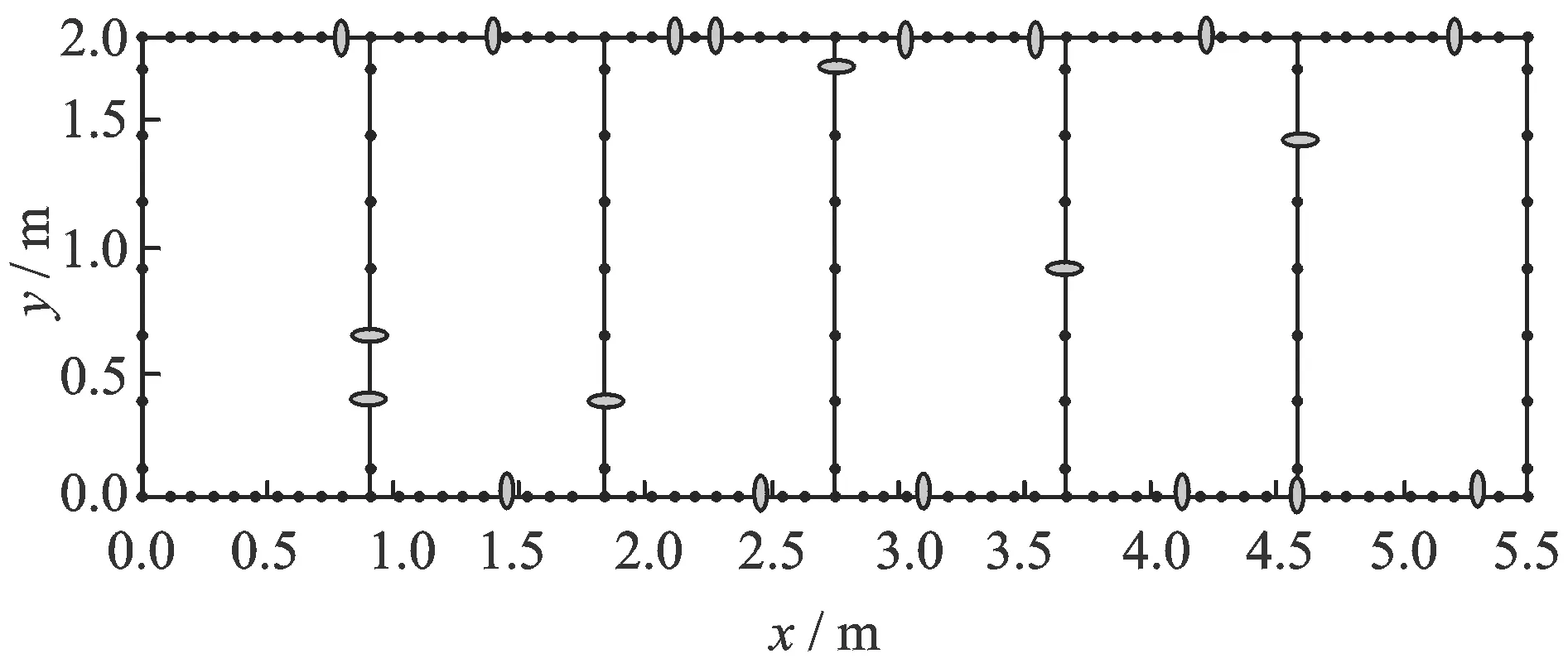
图5 基准模型基于原狼群算法的三维传感器布置

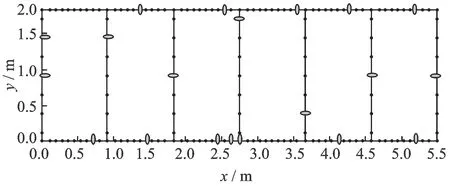
图6 基准模型基于分布式狼群算法的三维传感器布置

从表1中可以看出：1) 对于参数t，取值偏小较好，若t取值较大，计算得到的目标函数值比较差，即会影响狼群搜索能力，这里建议t取值为1；2) 搜索步长stepa，对狼群的局部搜索能力有很大的影响，若取值较小，搜索效果不好；若取值过大，则容易错过全局最优值，对搜索结果不利。stepa取值为2比较合适；3) 围攻步长stepb，若取值较小，导致算法的全局搜索能力降低；若取值较大，会因错过全局最优值而使得搜索结果较差。当其值为1时能够搜索到较优的极值，建议stepb取值1；4) 游猎搜索次数h×Nh，可以得出增多搜索次数可以提高整体的寻优能力，但提高的幅度有限，因此，建议Nh取值20，h取值为3。为便于与工况2进行对比，工况1中的数据采用上述分析建议的取值。

(2) 优化布置结果分析

表2给出了各种工况传感器布置方案的TMAC非对角元最大值。图3(a)给出了工况1布置20个传感器时的TMAC矩阵柱状图，此时TMAC非对角元最大值为0.001 9；图3(b)给出了工况2布置20个传感器时的TMAC矩阵柱状图，此时TMAC非对角元最大值为0.000 5，优化效果增幅73.68%，效果明显。但由于0.000 5和0.001 9远小于1，表现为在图(3)中TMAC柱状图的非对角元都非常小，很难对两种工况加以直观对比。为了更好地体现出本文所提出算法的有效性，图4给出了TMAC非对角元列向量最大值的比较。从图4可以看到，工况2的每阶模态列向量非对角元最大值都小于工况1，说明了DWA算法要优于WA。从表2中TMAC非对角元的最大值可以发现，工况2为0.000 5，而工况3为0.001 6，这说明对于结构所有的节点都布置传感器并不合理，不一定能得到最优布置效果，分析其原因是：模态置信准则的目的是实现各阶模态向量之间的可区分，即各阶模态向量之间的夹角最大化，但其权重矩阵用单位矩阵代替质量矩阵，使得各阶模态向量之间无正交性关系，因此会造成结构所有的节点都布置传感器并不合理的状况。图5和6给出了基准模型基于WA和DWA的三维传感器布置方案。

表2 不同传感器布置方案的TMAC非对角元最大值

4 结 论

本文建立了一种新的三维传感器优化布置准则，提出基于DWA的传感器优化布置的方法，并以基准模型为例进行验证，得到以下结论：

(1)针对MAC只能对结构的某一方向进行传感器优化布置研究，而不能确保在三个方向同时实现优化的问题，本文提出了TMAC，解决了三维传感器优化布置目标函数的问题。

(2)采用双重编码方式，有效地克服了原WA只能解决连续变量优化的问题；提出一种基于概率法判定阈值ε的方法，采用概率法初始化狼群个体，不仅加快了有效初始狼群的产生速度，而且保证了狼群个体各维分量的均匀性。

(3)引进了分组搜索的策略，狼群以组为单位并行搜索目标函数最优值，算例结果表明，分组并行搜索极大地加强了找寻大规模的目标最优值的能力。

(4)参数敏感性分析表明，狼群算法中的参数对算法的寻优效果影响较大，搜索步长和围攻步长如果偏小，则会降低算法的计算效率；如果偏大，则可能跳过全局最优解。每组中的狼个体淘汰数目不宜过多，否则会对算法的搜索能力和收敛速度不利；游猎搜索次数过多，对寻优能力的改善并不明显，还会增加算法的运行时间，应适当取值。

参考文献:

[1] 伊廷华,李宏男,顾明.结构健康监测中基于多重优化策略的传感器布置方法[J].建筑结构学报,2011,32(12):217—223.YI Tinghua, LI Hongnan, Gu Ming. Multiple optimization strategies based sensor placement method for structural health monitoring[J]. Journal of Building Structures,2011,32(12):217—223.

[2] Daniel C Kammer, Michael L Tinker. Optimal placement of triaxial accelerometers for modal vibration tests[J]. Mechanical Systems and Signal Processing, 2004,18(1):29—41.

[3] 江祥林,程高.基于EfI法的桥梁模态测试中传感器优化布置[J].桥梁建设,2012,42(2):59—65.JIANG XIANG-lin, CHENG Gao. Optimal sensor placement for bridge modal testing based on EfI method[J]. Bridge Construction,2012,42(2):59—65.

[4] He L J, Lian J J, Ma B, et al.Optional multiaxial sensor placement for modal identification of large structures[J]. Structural Control and Health Monitoring, 2013, DOI: 10.1002/stc.1550.

[5] 刘宇,毕丹,李兆霞.大跨斜拉桥基于遗传算法的传感器优化布置方法[J].东南大学学报,2009,39(4):825—829.Liu Yu, Bi Dan, Li Zhaoxia. Optimal placement of accelerometers in long cable-stayed bridges based on genetic algorithm[J]. Journal of Southeast University, 2009,39(4):825—829.

[6] Fidanova S, Marinov P, Alba E. Ant Algorithm for Optimal Sensor Deployment[M]. Computational Intelligence, Springer Berlin Heidelberg, 2012:21—29.

[7] 伊廷华,张旭东,李宏男.基于改进猴群算法的传感器优化布置方法研究[J].计算力学学报,2013,30(2):218—223.YI Ting-hua, ZHANG Xu-dong, LI Hong-nan. Research on optimal sensor placement based on improved monkey algorithm[J]. Chinese Journal of Computational Mechanics,2013,30(2):218—223.

[8] 鄢小虎,柳长安.基于生物智能的移动机器人路径规划研究[D].保定:华北电力大学,2010.YAN Xiao-hu, LIU Chang-an. Research on path planning for mobile robot based on the biological intelligence[D]. Baoding: North China Electric University, 2010.

[9] Carne T G, Dohmann C R. A modal test design strategy for modal correlation[A]. Proceedings of the 13th International Modal Analysis Conference,Schenectady[C]. New York,USA,February,1995.

[10] Yi T H, Li H N, Zhang X D. Sensor placement on Canton Tower for health monitoring using asynchronous-climb monkey algorithm[J]. Smart Materials and Structure,2012,21(12):1—12.

[11] Catbas F N, Caicedo J M, Dyke S J. Development of a benchmark problem for bridge health monitoring[A]. Proceedings of the International Conference on Bridge Maintenance, Safety and Management, IABMAS[C]． Porto, Portugal, July, 16-19, 2006.