高速磁悬浮电机转子低频振动干扰观测与抑制研究

刘 健， 郑世强， 房建成

(1.北京航空航天大学惯性技术重点实验室， 北京 100191； 2.新型惯性仪表与导航系统技术国防重点学科实验室， 北京 100191)

引 言

由于主动磁轴承(Active Magnetic Bearing)具有无机械磨损、无需润滑、可主动振动控制等优点[1]，得到了越来越多的研究和应用，随着磁悬浮技术的日益成熟，磁悬浮电机被广泛应用到诸如磁悬浮鼓风机、磁悬浮压缩机等高速旋转机械装备领域。相比传统的旋转机械装备，磁悬浮电机通常需要运行在高转速下才能提升整机系统的节能效率等性能指标。随着转速的提高，磁悬浮电机转子在高速时的失稳问题也逐渐凸显，提高磁悬浮转子在高速时的稳定性，保证磁悬浮电机在高速时的稳定运转是磁悬浮电机要解决的一个重要问题。磁悬浮电机转子在高速时失稳，其主要表征就是转速同频分量的增大和低频振动的增加，前者可以利用动平衡技术来解决。在保证磁悬浮转子具有较好的动平衡即在高速时具有较小的转速同频分量的情况下[2,3]，低频振动成为影响其高速稳定性的一个至关重要的因素，抑制磁悬浮转子在高速时的低频振动，可以有效提高其在高速时的稳定性。

对于大惯量扁平转子因陀螺效应引起的低频振动，相关领域的研究者进行了相关方面的研究[4,5]，也提出了有效的解决方法；而对于磁悬浮电机转子在高速时的低频振动，研究相对较少。现在大多数研究者选用先进控制算法来提高磁悬浮转子高速时的稳定性[6,7]，抑制低频振动，但很多先进控制算法运算复杂，再加上现用控制器在运算位数、处理速度等方面的限制，此方法不但不能有效抑制其低频振动，还会给系统带来更大的相位滞后，加剧其在高速时的不稳定。Jugo等利用频域模型对磁悬浮转子高速稳定性进行了研究[8,9]，分析指出磁悬浮转子在高速时低频振动的增大，造成了系统的失稳。但该文章仅限于理论分析，没有提出有效的解决方案。

本文利用改进型干扰观测器(Improved Disturbance Observer, IDOB)对磁悬浮电机转子在高速时的低频振动进行观测[10]，并在控制器中对其进行抑制。对100 kW磁悬浮电机运行在24 000 r/min转速时进行了实验验证。实验表明，该方法有效地克服了磁悬浮电机转子高速时形变的影响，对低频振动有很好的观测抑制作用，极大提高了磁悬浮电机转子高速时的稳定性。

1 IDOB原理分析

IDOB的实质为改进型干扰观测器，传统的干扰观测器需要实际系统的逆模型，逆模型的精度影响了整个观测器的精度，且需要一个高阶的低通滤波器来提高观测精度，低通滤波器的阶次越高，观测精度越高，但系统的鲁棒稳定性越低，工程应用越难实现[11，12]，两者之间的矛盾难以调和，对磁悬浮电机转子系统而言，低速时的模型和高速时模型之间存在一定的差异，其标称模型和逆模型很难精确获得，这使得传统干扰观测器不适用于磁悬浮转子系统高速时的低频振动观测抑制。为此，需对传统的干扰观测器进行优化，使其适合磁悬浮高速电机转子系统。

将磁悬浮电机高速时的低频振动等效为一种低频干扰，设其可由下式进行估计

(1)

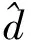
对于被控系统而言，设其传递函数为

(2)

将式(3)带入式(1)可得

(4)

由于磁悬浮电机转子高速时的模型误差,bm与λm，βn与an之间必然存在误差，设bm-λm=Δbm，βn-an=Δan，则式(4)的频域形式可表示为

(5)

磁悬浮电机转子在高速时的振动具有低频性，ω很小，s可以忽略，针对此特性，式(5)可以进一步简化为

(6)

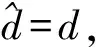
针对现用磁悬浮电机转子的现状，实验中，对式(1)的m和n都选取为1，对低频振动进行观测，式(1)可化为

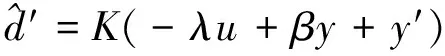
(7)

对式(7)进行拉普拉斯变换，可得

(8)

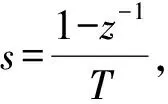
(9)

式中y(t)为当前时刻AD采样值，y(t-1)为上一时刻AD采样值，u(t)为当前时刻PID运算输出值。由此可见，此改进型干扰观测器相对于传统的干扰观测器，不仅更适于低频量的观测，而且更易于工程实现应用，具有很强的实用价值。

2 系统仿真分析

为了验证带有IDOB的主动磁轴承系统对低频振动的抑制效果，以原离散PID磁轴承控制系统为参考，将带有IDOB的主动磁轴承控制系统对低频振动的抑制效果与未加IDOB的原离散PID控制系统的抑制效果作对比。带有IDOB的整个主动磁轴承控制系统的仿真原理框图如图1所示。

图1中，实线框中的部分就是在未加IDOB时，主动磁轴承控制系统的仿真原理框图。首先对未加IDOB的主动磁轴承控制系统进行分析。

从转频输入端到位移输出端的系统传递函数为

(10)

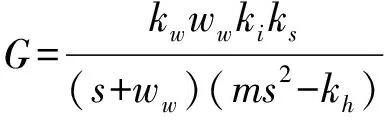
IDOB部分为图1中双点画线框内的部分，加入该部分后，图1整个框图是带有IDOB的主动磁轴承控制系统仿真原理框图，对整个原理框图的分析如下。带有IDOB的主动磁轴承控制系统，其从转频输入端到位移输出端的系统传递函数为

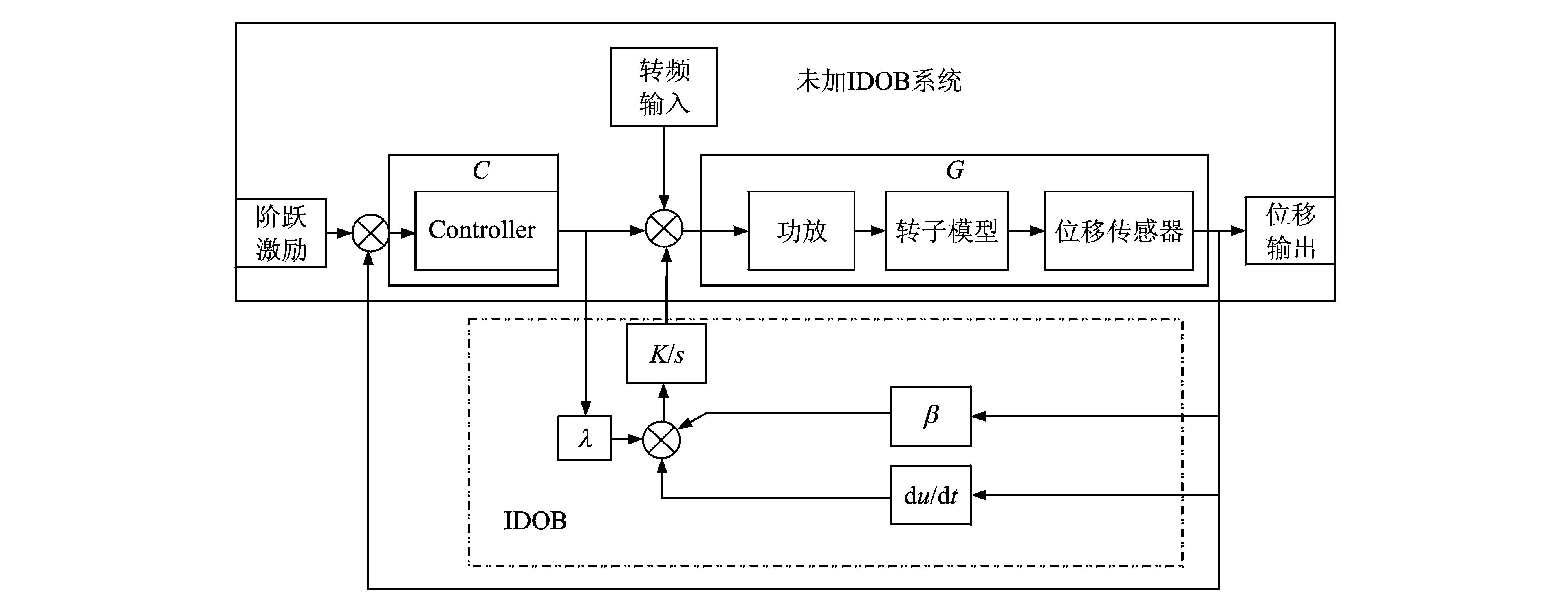
图1 加IDOB的主动磁轴承控制系统仿真框图

(11)

式中G和C与式(10)相同，K，β和λ为IDOB中的3个控制参数。

根据式(10)和(11)的传递函数，利用表1所示的仿真参数，可以得到未加IDOB的主动磁轴承系统与加IDOB的主动磁轴承系统在低频段(2～100 Hz)的幅频特性。

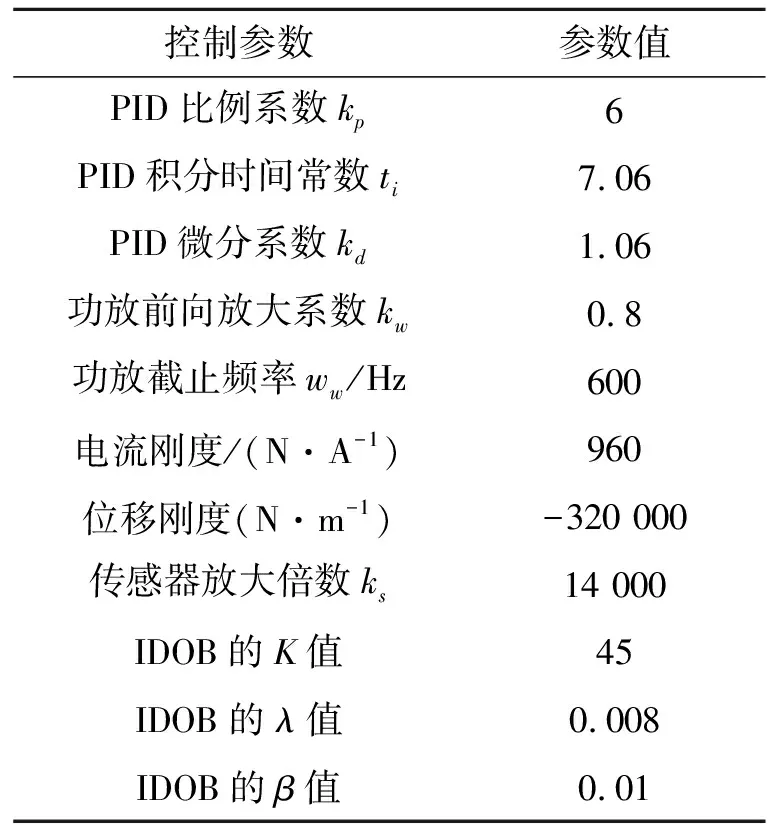
表1 Simulink仿真参数

未加IDOB的主动磁轴承系统与加IDOB的主动磁轴承系统低频段的幅频特性对比如图2所示。

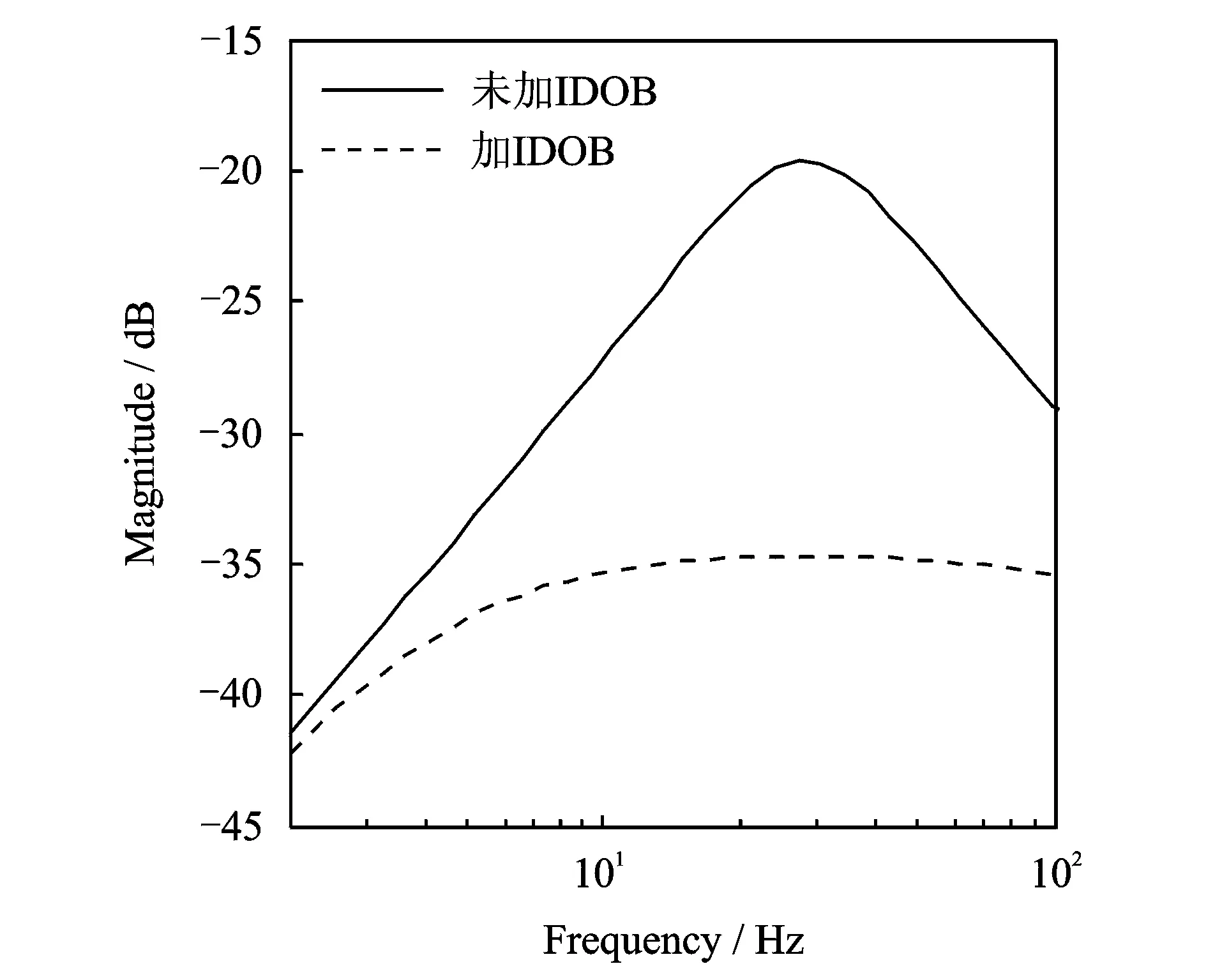
图2 未加IDOB系统与加IDOB系统低频段幅频特性对比图

从图2的幅频特性对比可以看出，加IDOB的主动磁轴承控制系统较未加IDOB的主动磁轴承控制系统，在2～100 Hz的低频频段范围内，对低频振动的幅值有更有效的衰减作用。

仿真系统中，阶跃信号初始值为0，在仿真时刻为1时，阶跃信号变为1，在系统外部输入一个幅值为0.5，频率为600 Hz的正弦信号作为主动磁轴承转子的转频量，未加IDOB的主动磁轴承控制系统转子位移与加IDOB的主动磁轴承控制系统转子位移仿真对比图如图3所示。

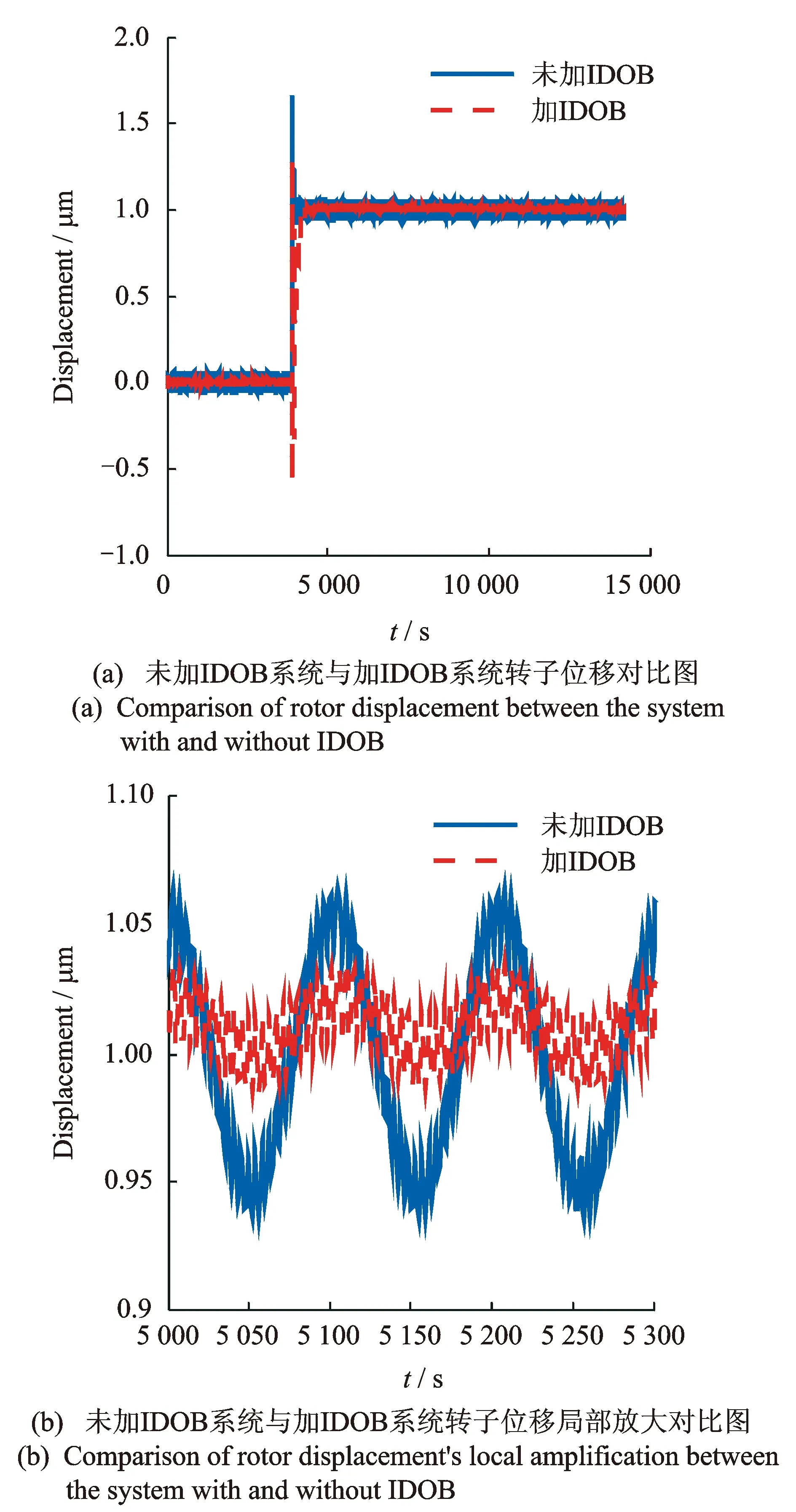
图3 未加IDOB系统与加IDOB系统转子位移对比图

由图3(a)可以看出，加IDOB的主动磁轴承控制系统相对于未加IDOB的主动磁轴承控制系统，对低频振动有更好的抑制效果。

图3(b)是主动磁轴承转子达到1的稳态时，取[5 000,5 300]时间段内波形的局部放大图。由图3(b)的稳态局部放大图可以得出，加IDOB的主动磁轴承转子低频振动量约为0.06，未加IDOB主动磁轴承转子低频振动量约为0.18，相对于原系统，加入IDOB的主动磁轴承系统，转子低频振动量减小了0.12，减小为原系统的33.3%，可见，加入IDOB的系统对于主动磁轴承转子的低频振动具有更好的抑制效果。

3 稳定性分析

加入IDOB的主动磁轴承转子系统，其稳定性受K，λ和β三个参数的影响，随着K的增大，式(11)传递函数的零极点分布趋势变化如图4所示。

由图4可以看出，随着K值的增大，系统出现了右半平面的极点，系统不再稳定，其临界稳定K值为57。

随着λ的增大，式(11)传递函数的零极点分布趋势变化如图5所示。

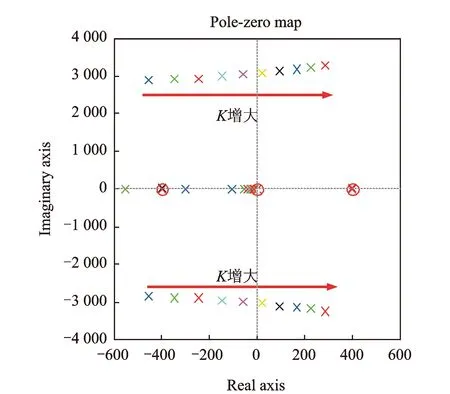
图4 K增大系统零极点分布趋势变化图

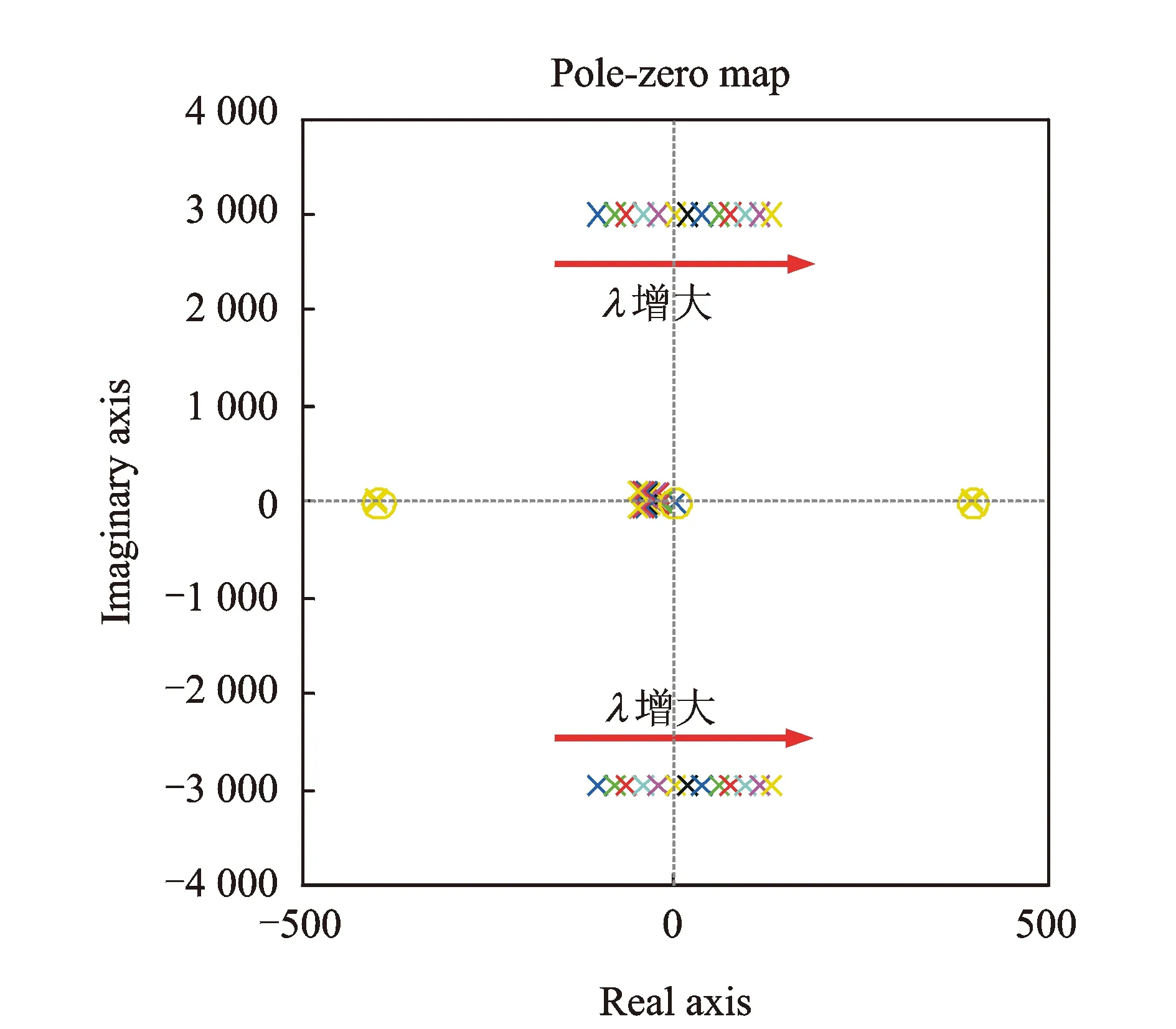
图5 λ增大系统零极点分布趋势变化图

由图5可以看出，随着λ的增大，系统出现了右半平面的极点，系统不稳定，其临界稳定的λ值是5.1。

随着β增大，式(11)传递函数的零极点分布趋势变化如图6所示。

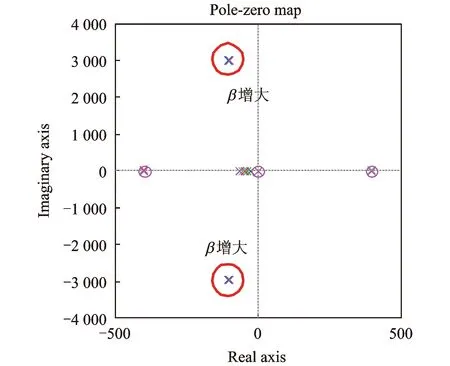
图6 β增大系统零极点分布趋势变化图

由图6可以看出，β的变化不影响主动磁轴承转子系统零极点分布，也不影响系统的稳定性。

综上所述，加入IDOB后主动磁轴承转子系统的稳定性随着K和λ的增大而降低，K的取值在[0,57]之间，λ的取值在[0,5.1]之间时，系统是稳定的，β值的变化基本不影响系统稳定性。

4 实验验证

为了验证IDOB的低频振动抑制效果，以100 kW电机为实验平台，在24 000 r/min转速时，做了对比实验验证。

实验中使用的100 kW电机是无刷直流电机，该电机是4极电机，采用4极分布式绕组，永磁体表贴的结构形式，电机控制采用的是两相导通，三相六状态的控制方式；该电机的磁轴承是纯电磁磁轴承，有两个径向磁轴承，分别位于电机的两端，一个轴向磁轴承位于电机的末端，磁轴承控制采用的是五自由度全悬浮的方式，两个径向磁轴承负责四个径向自由度的悬浮，一个轴向磁轴承负责一个轴向自由度的悬浮。实验中使用的100 kW磁悬浮电机的主动磁轴承系统的设计参数如表2所示。

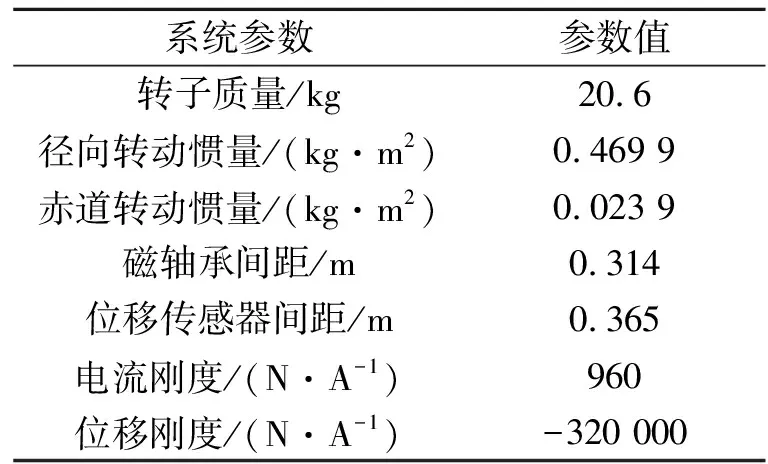
表2 100 kW磁悬浮电机主动磁轴承系统参数

实验中使用的100 kW磁悬浮电机磁轴承系统的径向控制参数如表3所示。

在选取上述IDOB参数的情况下，主动磁轴承转子闭环系统的零极点分布如图7所示。

由图7可以看出，在选取上述IDOB参数的情况下，主动磁轴承转子闭环系统是稳定的，在此基础上，进行升速实验，实验系统实物图如图8所示。

在24 000 r/min转速时，加入IDOB的主动磁轴承系统与未加IDOB的主动磁轴承系统的位移波形对比如图9所示。

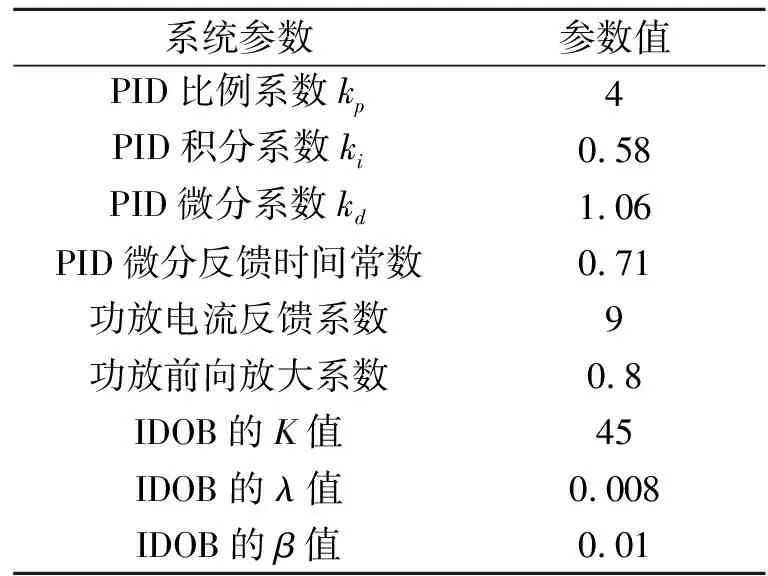
表3 100 kW磁悬浮电机磁轴承系统的径向控制参数

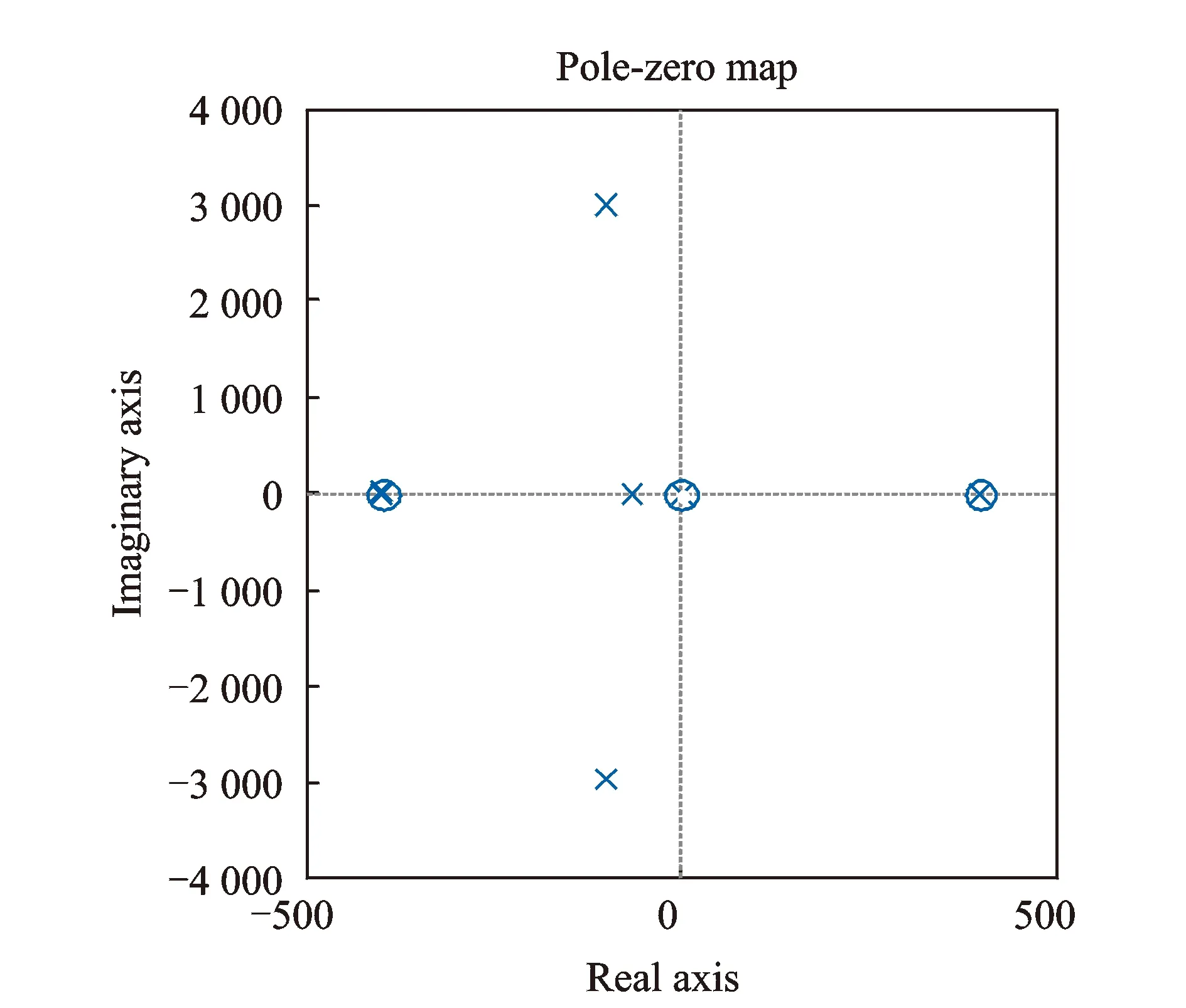
图7 主动磁轴承转子闭环系统零极点分布图

图8 100 kW磁悬浮电机实验平台

由图9可以看出，原系统未加IDOB，主动磁轴承转子在24 000 r/min转速时低频增益为-30 dB，径向BY通道位移跳动量为57.6 μm，加IDOB的主动磁轴承系统在24 000 r/min转速时低频增益为-50 dB，径向BY通道位移跳动量为20.8 μm，相比于原系统，加入IDOB的主动磁轴承系统低频增益减小20 dB，位移跳动量减小36.8 μm，控制精度提高了63.89%。实验结果表明，离散PID控制器加IDOB能很好地抑制主动磁轴承转子在高速时的低频振动，提高主动磁轴承转子系统的稳定性。

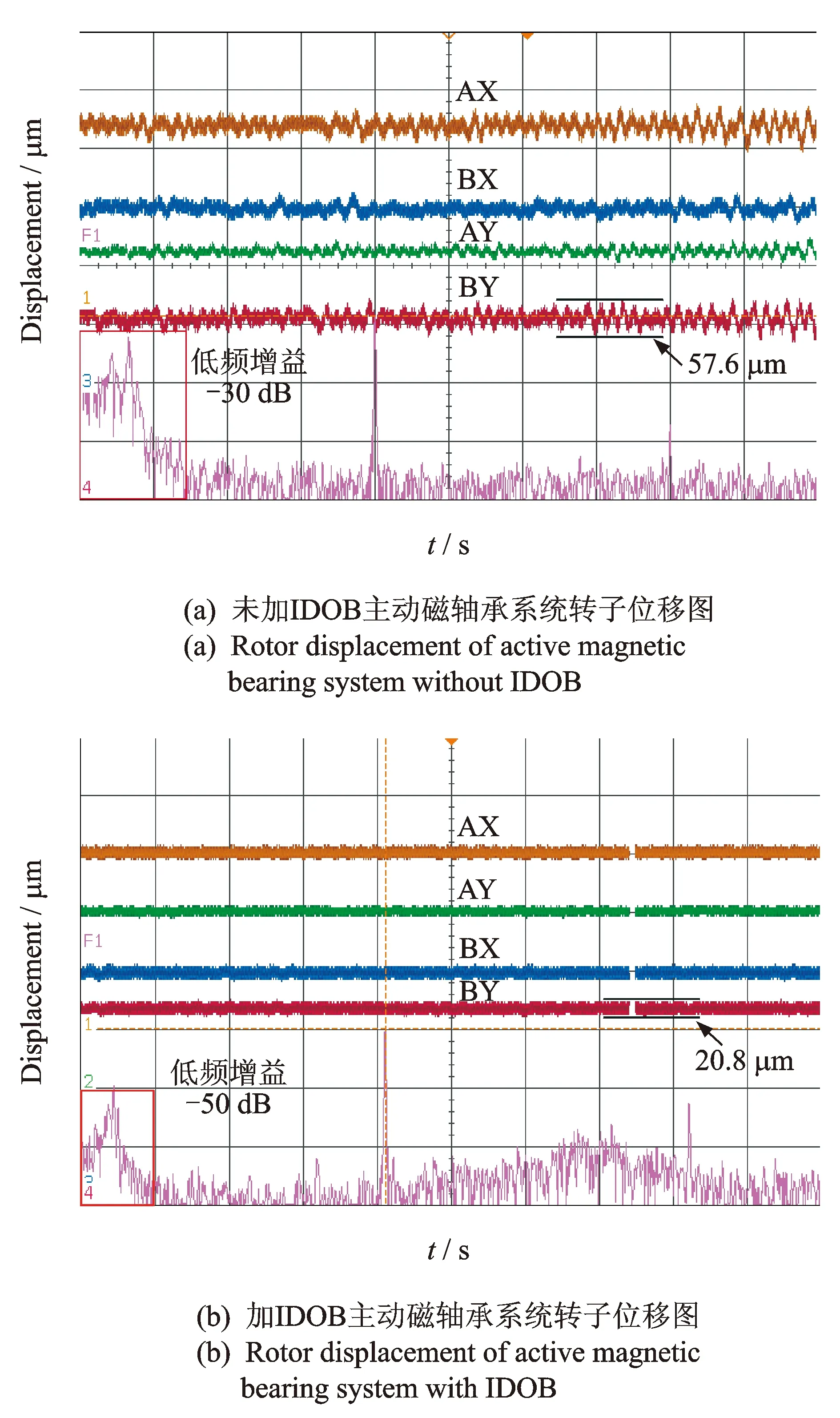
图9 主动磁轴承转子升速位移对比图

5 结 论

本文针对磁悬浮电机转子高速时低频振动加剧，稳定性变差的问题，提出利用改进型干扰观测器——IDOB对低频振动进行观测，并在控制器中进行消除的方法，用来抑制磁悬浮电机转子在高速时的低频振动，提高磁悬浮电机转子高速时的稳定性。升速实验结果表明，加入IDOB后的主动磁轴承系统相较于原系统，在24 000 r/min转速时低频增益减小20 dB，转子跳动量减小36.8 μm，控制精度提高了63.89%，由此说明，IDOB的加入能很好抑制磁悬浮电机转子高速时的低频振动，改善其高频特性，提高高速时的稳定性。

参考文献：

[1] 施韦策 G,布鲁勒 H,特拉克斯勒 A.主动磁轴承基础、性能及应用[M].虞烈，袁崇军，译．谢友柏，校．北京:新时代出版社,1997.Schweitzer G, Bleuler H, Traxler A. Basics, Properties and Applications of Active Magnetic Bearings[M]. Beijing: New Times Press, 1997.

[2] 谢振宇,牟伟兴,周红凯,等.基于转速的磁悬浮轴承转子系统变参数控制[J]. 振动工程学报,2012,25(6):739—744.XIE Zhenyu, MOU Weixing, ZHOU Hongkai, et al. Varying parameter control of active magnetic bearing rotor system based on rotation speed[J]. Journal of Vibration Engineering, 2012,25(6):739—744.

[3] 章琦,祝长生.电磁悬浮飞轮转子系统的模态解耦控制[J]．振动工程学报,2012,25(3):302—310.ZHANG Qi, ZHU Changsheng. Modal decoupling control for active magnetic bearing-supported flywheel[J]. Journal of Vibration Engineering, 2012,25(3):302—310.

[4] 郑世强,房建成.MSCMG磁轴承μ综合控制方法与实验研究[J].仪器仪表学报,2010,31(6):1 375—1 380.Zheng Shiqiang, Fang Jiancheng. Experimental study on μ synthesis control for magnetic bearings of MSCMG[J]. Chinese Journal of Scientific Instrument, 2010,31(6):1 375—1 380.

[5] Fang Jiancheng, Zheng Shiqiang. AMB vibration control for structural resonance of double-gimbal control moment gyro with high-speed magnetically suspended rotor[J]. IEEE Asme Transactions on Mechatronics, 2013,18(1):32—43.

[6] 赵雪山.永磁偏置径向轴向磁轴承H∞控制系统的研究[D].南京:南京航空航天大学,2004.Zhao Xueshan. Research on the H∞control system in the radial-axial magnetic bearing biased with permanent magnets[D]. Nanjing: Nanjing University of Aeronautics and Astronautics, 2004.

[7] Alexander Smirnov, Rafal P Jastrzebski, Katja M Hynunen. Gain-scheduled and linear parameter-varying approaches in control of active magnetic bearings[A]. Proceedings of the 12thInternational Symposium on Magnetic Bearings[C]. Wuhan, China, 2010:350—360.

[8] Jugo J, Lizarrage I, Arredondo I. Nonlinear modeling and analysis of active magnetic bearing systems in the harmonic domain: a case study[J]. IET Control Theory Appl, 2008,2(1):61—71.

[9] Jugo J, Lizarrage I, Arredondo I. Nonlinear analysis of an AMB system using harmonic domain LTV models[A]. IEEE Int. Conf. Control Applications[C]. Munich, Germany, October 2006, 271—276.

[10] 王英,熊振华,丁汉.直线电机运动控制中的干扰观测器的研究[J].中国机械工程,2004,15(17):1 549—1 552.WANG Ying, XIONG Zhenhua, DING Han. Research on disturbance observer for linear motion control[J]. China Mechanical Engineering, 2004,15(17):1 549—1 552.

[11] Umeno Takaji, Hori Yoichi. Robust speed control of dc servomotors using modern two degrees-of-freedom controller design[J]. IEEE Transactions on In-dustrial Electronics, 1991,38(5):363—368．

[12] Chen W H. Disturbance observer based control for nonlinear systems[J]. IEEE Trans. Mechatronics, 2004,9(4):706—710.