SVD分量包络检测方法及其在滚动轴承早期故障诊断中的研究

冷永刚， 郑安总, 范胜波

(1.天津大学机械工程学院， 天津 300072；2.天津大学机构理论与装备设计教育部重点实验室， 天津 300072)

引 言

滚动轴承是旋转机械中最常用的关键部件之一。滚动轴承运行正常与否直接关系到整个旋转机械的运行状态。因此,滚动轴承故障的检测和诊断技术一直是研究的重点和热点。当滚动轴承出现局部损伤后,其元部件之间的相对周期性运动会使得损伤部位产生周期性冲击,从而使得轴承在较宽频率范围内被激励并产生冲击衰减响应。在滚动轴承故障的早期阶段,由故障所引起的冲击成分能量在整个轴承系统振动总能量中所占的比例较小,且分布在较宽广的频率范围内。同时,大量的机械设备中其他运动部件和结构的信息以及环境的干扰也会被引入到轴承系统形成背景噪声,从而使得滚动轴承的早期故障难以检测和诊断。

频谱分析是一种经典的信号分析。傅立叶变换在频域上是完全局部化的,但由于其基函数在时域上的全局性,使得傅立叶变换没有任何的时间分辨率,因此傅立叶变换只适合于处理平稳信号。而滚动轴承振动信号中的冲击信号是非平稳信号。因此傅立叶变换很难适应滚动轴承故障信号的分析。包络解调分析在滚动轴承故障中广泛应用[1～3],但在早期故障情形下,背景噪声很强以至于不能准确获取有效的包络信号使得该方法也不能很好应用。

奇异值分解(Singular Value Decomposition, SVD)是一种非线性滤波方法,广泛应用于信号的消噪和检测工作中[4～6]。常规的基于奇异值分解降噪的方法要求特征信号在信号中占主要成分,这样经奇异值分解得到的前几阶较突出的奇异值对应了信号空间，而其余较小的奇异值对应了噪声空间,只要保留前几阶较突出的奇异值所对应的降维矩阵,就可以很好地得到降噪后的信号。然而当背景噪声很强时,特征信号完全被噪声淹没，此时经奇异值分解后不能得到突出的奇异值，因而无法用奇异熵方法确定信号奇异谱降噪阶次[7]，也无法用奇异谱差分谱方法确定有用分量信号的个数[8,9]，因此也就不能提取到特征信号。为了克服这一问题，本文提出了SVD分量包络检测方法检测滚动轴承早期故障。该方法先进行SVD，寻找到隐藏故障信号的子空间,然后逆变换子空间得到分量信号。将得到的分量信号再经过包络分析即可得到分量信号对应的包络信号，在该包络信号中可找到轴承早期故障的特征状态,从而实现滚动轴承早期故障的准确诊断。

1 奇异值分解与重构原理[5]

SVD从矩阵的角度出发,将包含信号信息的矩阵分解到一系列奇异值和奇异值矢量对应的子空间中。

对m×n的实矩阵A(不妨假设m>n),其奇异值分解可表示为

A=UΣVT

(1)

式中U为m×m阶正交矩阵且满足UUT=I；V为n×n阶正交矩阵且满足VVT=I；Σ=diag(σ1，σ2，…，σn)是按降序排列的对角矩阵,其对角元素为矩阵A的奇异值。

对实际采样得到的一维时间序列X=(x(1)，x(2)，…，x(N)),为了能用SVD方法处理,构造它的Hankel矩阵如下

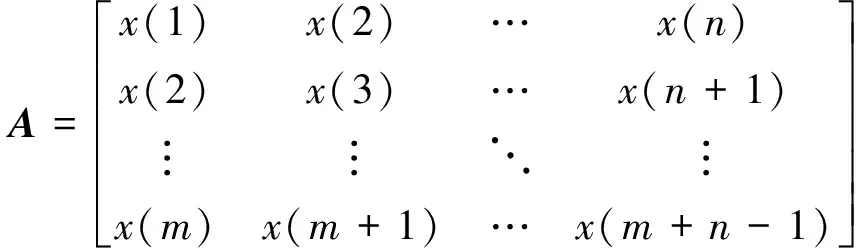
其中N=m+n-1。

根据SVD分解的特点,将矩阵A改写成用向量ui和vi及奇异值σi相乘的形式

(2)

因此矩阵A经过SVD分解后等于一系列与奇异值σi相对应的子矩阵Ai相加之和。根据Hankel矩阵的结构形式,子矩阵Ai可以表示如下

根据上述一维时间序列到Hankel矩阵的变换形式,对子矩阵进行逆变换求得分量信号Pi。即取子矩阵Ai的第一行和最后一列的元素(最后一列除去第一个元素)构成分量Pi信号。按照此变换构成的所有分量信号Pi就形成了对原始采样信号的分解。已证明这样获得的n个分量信号线性叠加的结果就是原始采样信号,即

X=P1+P2+…+Pn

(3)

2 包络分析

包络分析通过对调幅信号进行解调分析,去除掉高频载波信号获取低频包络信号。包络分析的核心是Hilbert变换。设时间信号x(t),其Hilbert变换为

(4)

构造解析信号

Z(t)=x(t)+jH[x(t)]=a(t)ejΦ(t)

(5)

于是得到幅值函数

(6)

幅值函数a(t)即为原时间信号x(t)的包络信号。

3 SVD分量包络方法分析过程

为了在滚动轴承系统复杂的调幅振动下检测出早期故障特征,本文提出了SVD分量包络检测方法来检测滚动轴承早期故障特征,其具体过程如下:

(1)对一维采样时间序列X构造Hankel矩阵,将信号延拓到n维空间A；

(2)对矩阵A进行SVD分解后再逆变换得到n个分量信号Pi(i=1，2，…，n);

(3)对每个分量信号Pi进行Hilbert变换,求得解析信号Zi(t),然后求出相对应的幅值函数ai(t)；

(4)对包络信号ai(t)进行FFT变换得到该包络信号的频谱。在得到的n个包络信号频谱中可提取到一组清晰的故障特征。

上述过程实际上是将一维采样时间序列X中丰富的振动信息延拓到高维空间A中,并将隐藏的振动信息在高维空间中展开,之后再经SVD处理可提高隐藏特征信息的信噪比。随后经Hilbert变换可得到对应故障的特征。

4 滚动轴承早期故障的仿真分析

为了便于分析,将实际滚动轴承系统简化为仅有单模态的阻尼系统。根据文献[10]建立滚动轴承出现单点局部损伤时传感器所采集到的信号模型:

(7)

m(t)=A[1+Bcos(2πf1t)]

(8)

式中m(t)为脉冲幅值调制函数,f1为第一调制频率,是轴的转频或滚动体的公转频率。外圈故障信号不受转频的调制,所以令m(t)=A=0．000 000 04。故障特征周期T=1/30 s,即第二调制频率1/T=30 Hz,并取轴承系统模态频率f2=3 000 Hz。U(t)为单位阶跃函数,n(t)为噪声。取轴承系统阻尼比ζ=0.1,计算得冲击信号衰减指数c=2πζf2=1 885 s-1。图1(a)给出了脉冲衰减响应的仿真图。将轴承系统中存在的背景噪声n(t)简化为高斯白噪声下轴承系统的响应

(9)

式中ωn=2πf2,高斯白噪声w(t)满足E[w(t)]=0，E[w(t)w(t-τ)]=2Dδ(τ),其强度为D=6。高斯白噪声下的系统响应用四阶Runge-Kutta算法求解得到。 图1(b)给出了脉冲衰减信号和系统噪声线性叠加后得到滚动轴承早期故障的仿真信号,图1(c)给出了其频谱。

图1(d)给出了仿真信号的包络谱,从图1仿真信号的时域图(b)、频谱(c)以及和包络谱(d)中均看不到周期性的脉冲故障特征频率,即故障特征信号被强噪声所淹没。FFT方法和包络分析方法均无法提取故障特征。下面应用本文提出的方法分析

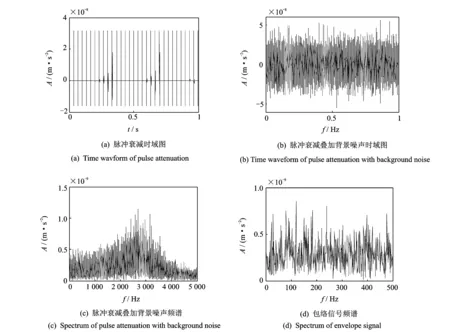
图1 滚动轴承系统仿真信号分析

仿真信号。

考虑实际轴承的故障形式并经大量测试分析能够确定针对该轴承故障信号，SVD重构空间维数n=3时有较好结果，仿真时同样取重构空间维数n=3。图2给出了轴承仿真信号经奇异值分解和包络分析后得到的3个分量信号的时域图和包络谱。在图2的分量信号P1和P2分析图中,既无法从时域图中看到冲击故障信号,也无法从包络谱中找到故障特征频率。这是因为此时分解出来的分量信号P1和P2中主要包含轴承系统的共振信息,而故障信息含量很少。由于分量信号P1和P2提取了大部分的高频振动信号,同时剩下了较多故障信息。正因为如此,在P3的包络谱中观察到了非常明显的故障特征频率谱峰及其倍频谱峰。

5 工程实验验证

滚动轴承早期故障模拟实验在滚动轴承试验台上进行。所用滚动轴承型号为N205EM,滚动轴承故障类型为外圈损伤,即在外圈表面线切割一宽0.2 mm,深0.1 mm的沟槽来模拟早期轻微故障。实验过程中采样频率是10 kHz，分析点数是10 000点，轴承各项参数如表1所示。

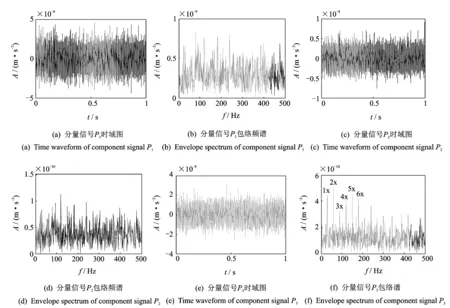
图2 仿真故障信号的分量信号及其包络分析

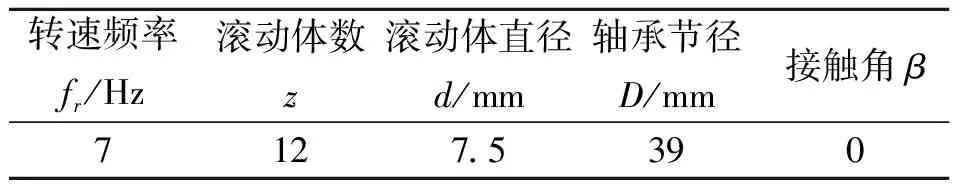
表1 实验轴承各项参数

滚动轴承出现外圈损伤的特征频率计算式为[11]

(10)

由式(10)和表1参数计算得到故障特征频率f0=33．92 Hz。

图3(a)和(b)分别给出了滚动轴承早期故障模拟实验得到的原始采集信号时域图及其频谱。由于滚动轴承故障早期阶段损伤很小,冲击信号被背景噪声所淹没,因此在时域图中很难观察到冲击信号,而从其频谱图中只能看出轴承系统的宽频激励响应,其振动能量主要集中在系统的模态频率处。图3(c)和(d)分别给出了原始采集信号的包络信号时域及其包络谱图,可以看到轴承系统振动中包含丰富的振动信息,但轴承的早期故障特征却很难观察到。

针对图3原始采集信号,采用本文提出的方法分析。取空间重构维数n=3。按照前面提到的SVD分量包络方法分析过程对原始采集信号进行处理。图4给出了分量信号P1到分量信号P3的时域波形和包络谱。

从图4(a)的SVD分量信号P1时域波形中完全看不到冲击现象,该分量谱能量主要集中在轴承系统高频区域。这是因为SVD首先提取信号中最主要的高频共振振动能量成分。图4(b)给出了分量信号P1的包络谱,可以看出在包络谱里存在很多干扰信号,无法反映并检测到低频的轴承故障特征信息。

对于SVD第二个分量信号P2的时域波形图4(c)及其包络谱图4(d),可以看到不太明显的周期性冲击与不太清晰的故障特征频率谱峰,这是因为经奇异值分解得到的分量信号P2,除了继续提取系统剩余高频共振振动能量信息外,同时P2还提取了宽带范围内的振动能量信息。由于轴承的故障信息

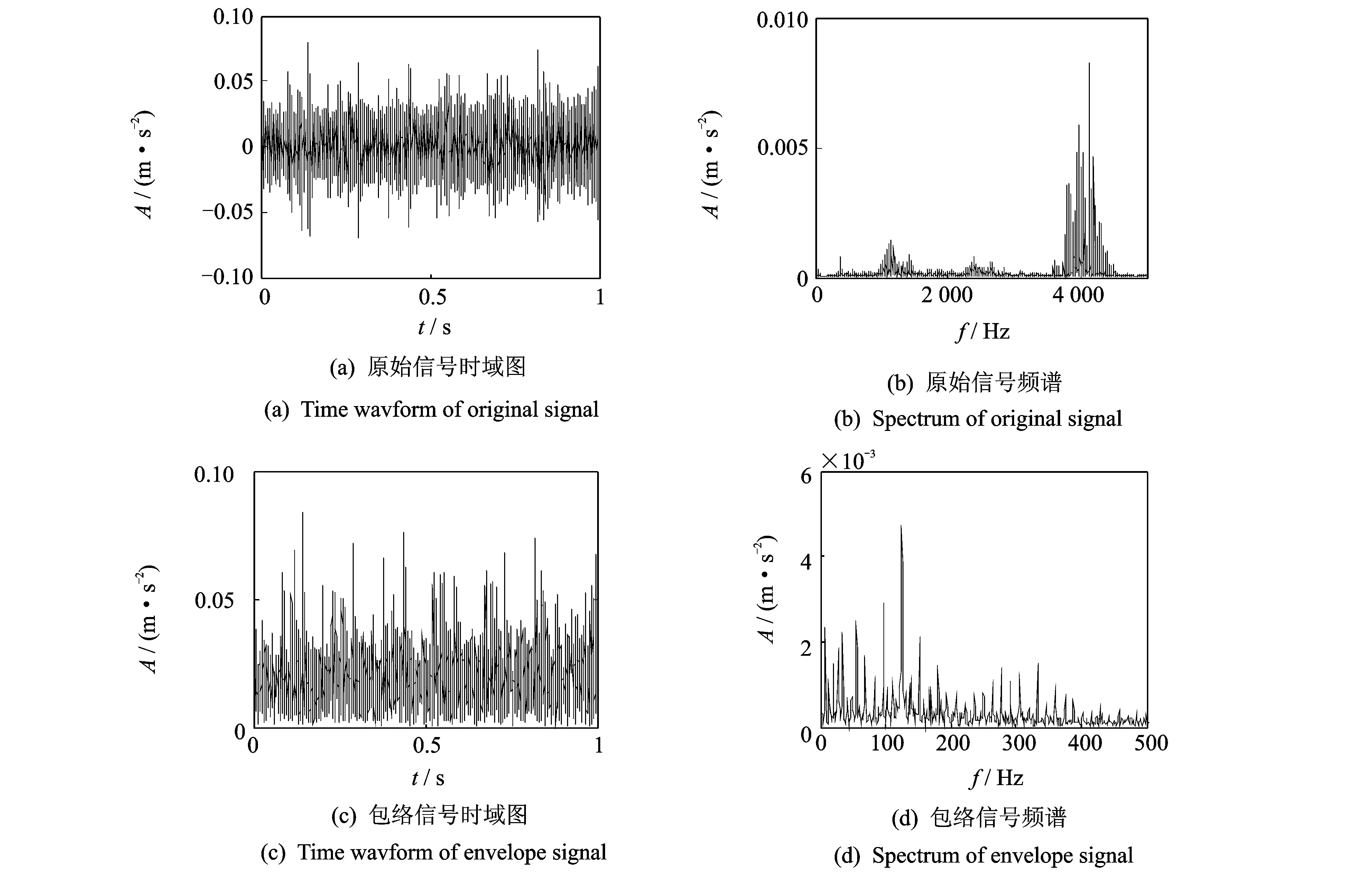
图3 滚动轴承故障信号分析

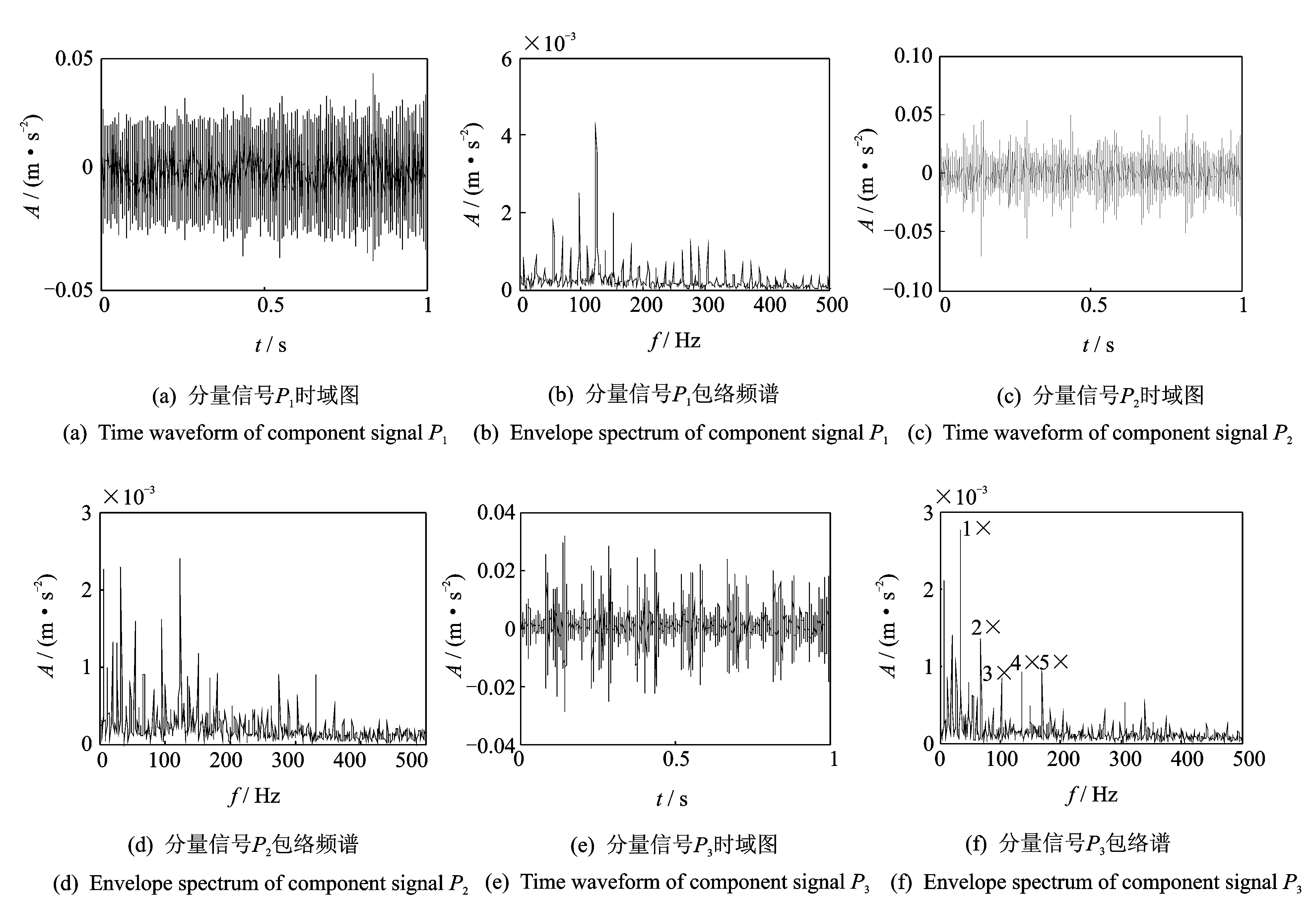
图4 故障信号的分量信号及包络分析

能量太弱,因此无法清晰检测到轴承故障特征频率谱峰。

图4(e)的SVD分量信号P3的时域波形中出现了明显的周期冲击,这是因为该分量不再含有很强的噪声和高频振动的能量信息,而故障信号保留了较多的成分,因此在P3的包络谱图4(f)中得到了明显的故障特征频率峰及其2,3,4等倍频信号峰,这说明分量信号P3的包络分析,可从原始采集信号中清晰分离出轴承的早期故障特征。

6 总 结

滚动轴承运行的振动信息非常丰富,当滚动轴承出现早期故障时,其故障特征信息往往隐藏在这些振动信息中而很难识别。本文根据SVD能够在高维空间中提取隐藏信息的特性以及Hilbert变换的包络性质,提出SVD分量包络分析的滚动轴承早期故障检测方法。该方法可将一维采样时间序列变换到高维空间中,然后经SVD和Hilbert变换处理,就能够检测到滚动轴承的早期故障特征。仿真模拟与工程实验验证了所提方法的有效性。

参考文献：

[1] Randall R B,Antoni J,Chobsaard S．The relationship between spectral correlation and envelope analysis in the diagnostics of bearing faults and othercyclostationary machine signals[J]. Mechanical Systems and Signal Processing,2001, 15(5):945—962．

[2] 张中民,卢文祥,杨叔子，等．滚动轴承故障振动模型及其应用研究[J]．华中理工大学学报,1997,25(3) :50—53．Zhang Zhongmin,Lu Wenxiang,Yang Shuzi, et al．A model for the vibration produced by local faults in roller bearing and its application[J]．Journal of Huazhong University of Science and Technology,1997,25(3) :50—53．

[3] 田涛,丁康．希尔伯特变换及其在故障诊断中的应用[J]．振动与冲击,1996,15(2) :23—27．Tian Tao,Ding Kang．Hilbert transform and its application in the failure diagnosis[J]．Journal of Vibration and Shock,1996,15(2) :23—27．

[4] 赵学智,陈统坚,叶邦彦．基于奇异值分解的铣削力信号处理与铣床状态信息分离[J]．机械工程学报,2007,43(6) :169—174．Zhao Xuezhi,Chen Tongjian,Ye Bangyan．Processing of milling force signal and isolation of state information of milling machine based on singular value decomposition[J]．Chinese Journal of Mchanical Engineering,2007,43(6):169—174．

[5] 赵学智,叶邦彦,陈统坚．奇异值差分谱理论及其在车床主轴箱故障诊断中的应用[J]．机械工程学报,2010,46(1):100—108．Zhao Xuezhi,Ye Bangyan,Chen Tongjian．Difference spectrum theory of singular value and its application to the fault diagnosis of headstock of lathe[J]．Chinese Journal of Mechanical Engineering,2010,46(1) :100—108．

[6] 吕勇,李友荣,王志刚,等．基于奇异值分解及包络分析的齿轮局部故障特征提取[J]．机床与液压,2007,35(5) :217—219．Lv Yong,Li Yourong,Wang Zhigang,et al．Gear local fault identification using singular value decomposition and enveloping analysis[J] ．Machine Tool & Hydraulics,2007,35(5) :217—219．

[7] 杨文献, 姜节胜. 机械信号奇异熵研究[J]. 机械工程学报, 2000, 36(12): 9—13.Yang Wenxian, Jiang Jiesheng. Study on the singular entropy of mechanical signal[J]. Chinese Journal of Mechanical Engineering, 2000, 36(12): 9—13.

[8] 赵学智, 叶邦彦, 陈统坚. 奇异值差分谱理论及其在车床主轴箱故障诊断中的应用[J]. 机械工程学报, 2010, 46(1): 100—108.Zhao Xuezhi, Ye Bangeyan, Chen Tongjian. Difference spectrum theory of singular value and its application to the fault diagnosis of headstock of lathe[J]. Chinese Journal of Mechanical Engineering, 2010, 46(1): 100—108.

[9] Zhao Xuezhi, Ye Bangyan. Selection of effective singular values using difference spectrum and its application to fault diagnosis of headstock[J]. Mechanical Systems and Signal Processing, 2011,25: 1 617—1 631.

[10] McFadden P D, Smith J D. Model for the vibration produced by a single point defect in a rolling element bearing[J]. Journal of Sound and Vibration, 1984, 96(1):69—82.

[11] Lin Jing,Qu Liangsheng．Feature extraction based on morlet wavelet and its application for mechanical fault diagnosis[J]．Journal of Sound and Vibration,2000,234(1) :135—148．