基于ANSYS 的元结构选型与优化

黄晓华，仇家强，刘奇，王可，张健

(南京理工大学 机械工程学院，江苏 南京 210094)

0 引言

现代机床正向高速、大功率、高精度的方向发展，随着加工精度和切削速度的不断提高，对机床动态特性提出了更高的要求。利用有限元方法研究机床动态性能已经成为设计和优化机床结构的重要手段和发展趋势。基于元结构的动态优化方法，分别从结构件内部结构和外部轮廓进行优化，有效解决了复杂结构的优化问题。文献［1］提出了基于元结构的优化方法，并用该方法对床身进行动态优化。文献［2］建立了元结构方法的理论模型，并证明了该方法的可行性。文献［3－5］运用该方法对机床结构进行了动态优化。本文针对传统元结构选型过程中，存在备选元结构局部尺寸完全由经验确定、质量不统一等问题，提出新的选型方法，并通过两种典型元结构动态特性的分析、比较，验证新选型方法的可行性。

1 基于元结构的结构优化方法

1.1 基于元结构的结构优化方法简介

元结构指把机械结构大件按其组成的形体进行分解，最终可分解得一些拓扑结构变化不大、相对独立的基本单元结构［1，6］。如床身等结构件中“井”字形筋板形成的一系列立方体筋格元结构。通过改善元结构的拓扑形状和优化其尺寸比例，可有效提高结构件动态性能。基于元结构的动态优化包含以下几个过程:提取元结构和框架结构→元结构动态优化→框架结构动态优化→建立整体结构的变量化模型→选取设计变量进行结构优化［7］。

1.2 元结构选型方法

元结构的动态优化包含元结构的选型和尺寸优化两方面的内容，当需要改变元结构的拓扑形状时就涉及到元结构的选型问题。常见的元结构选型流程如图1(a)，其备选元结构尺寸完全由经验确定，可通过比较元结构单体的动态特性来选定元结构型式。该选型过程存在以下不足:1)备选元结构的尺寸比例由经验确定，未经优化，直接比较不能保证选型的正确性，如文献［5］中两种元结构尺寸的选定;2)元结构局部尺寸的选择具有一定的任意性，备选元结构间存在一定的质量差。文献［3］提及使备选元结构质量大致相等，但没有给出具体的解决方法。当注重结构的轻量化时，质量指标在综合性能中占有一定的权重，不可忽视;3)未给合实际结构考虑元结构扩展后的动态性能。

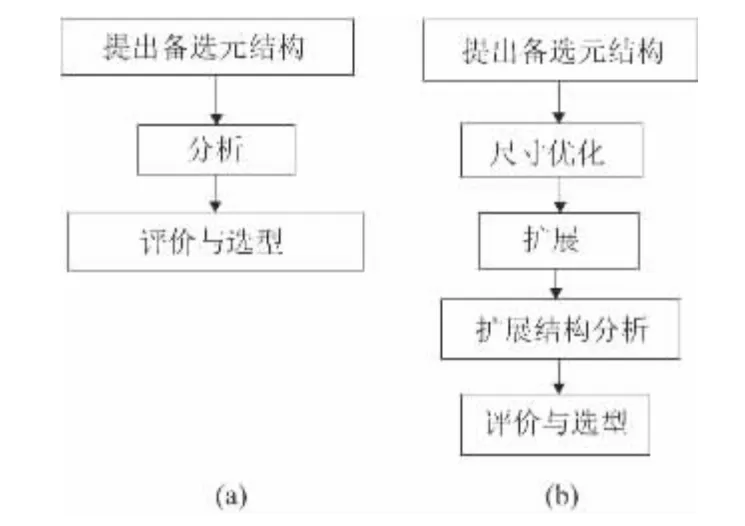
图1 元结构选型流程

为解决以上不足，本文提出如图1(b)所示的选型方法。先根据实际需要提出备选元结构，并在ANSYS 优化模块中优化备选元结构的尺寸比例。在优化过程中，通过设置统一的最大质量约束，使得优化后备选元结构动态性能均达到最优的同时，质量基本一致。由于扩展结构更接近实际结构，其动态特性也更能体现实际结构件的动态特性，因此，先将尺寸优化后的元结构进行扩展，再根据扩展结构的动态性能选定元结构的型式。以下将以两种典型元结构的比较，进行详细分析和说明，验证新方法的可行性。

2 元结构单体及扩展结钩动态特性分析

2.1 元结构单体间的分析比较

目前机床床身中典型的元结构型式如图2 所示。

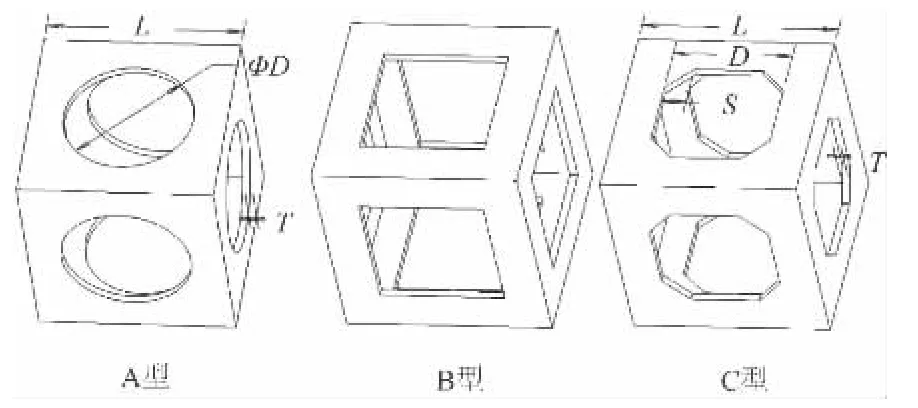
图2 典型元结构

A 型为在六面体的每个面开圆形出砂孔;B 型为六面体的每个面开正方形出砂孔;C 型为B 型的改进型，在方形出砂孔的每个直角处加入过渡斜角。

在ANSYS 中建立A 和C 型的参数化模型，进行尺寸迭代优化。虽然实际元结构不一定都为等边长的立方体，但对其进行分析具有代表性。统一立方体元结构边长为L=300 mm(取筋板厚度中心距离)，铸铁材料弹性模量E=1.3e5 MPa，密度ρ=7 350e9 kg/mm3，泊松比μ=0.27。

设计变量:如图2 所示，对A 型，选择圆形出砂孔的直径D、筋板厚度T 作为设计变量;对C 型，选方形出砂孔的边长D、过渡斜角的直角边长S 和筋板厚度T 作为设计变量。

状态变量:选定元结构的质量作为约束变量。优化设计过程中，备选元结构的最大质量约束条件一致。

目标函数:对于动态优化设计，可选低阶频率、振型幅值等动态指标构成目标函数。本文以提高元结构的低阶频率作为优化的目标，由元结构前三阶固有频率构成目标函数。由于ANSYS 优化设计总是使目标函数值最小，且为正值［8］，从提高结构低阶频率出发，构造目标函数F 为:

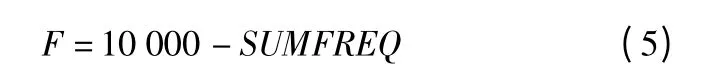
式中:

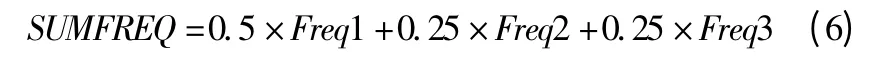
Freq1、Freq2、Freq3 分别为元结构的一、二、三阶固有频率。选用一阶优化方法，最大质量约束条件为90 kg时，目标函数F 的迭代曲线如图3 所示。在不同质量约束条件下，最优尺寸比例如图4 及图5 所示，优化后元结构的前三阶固有频率及实际质量如表1 所示。

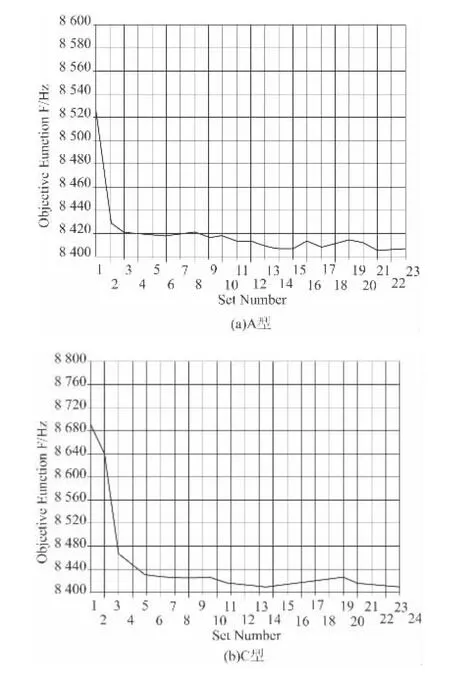
图3 目标函数F 迭代曲线

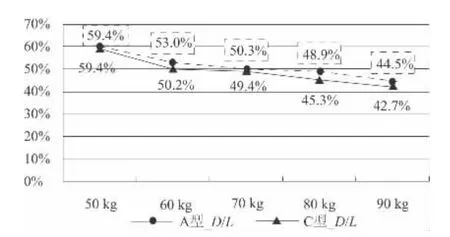
图4 最优尺寸比例D/L 曲线

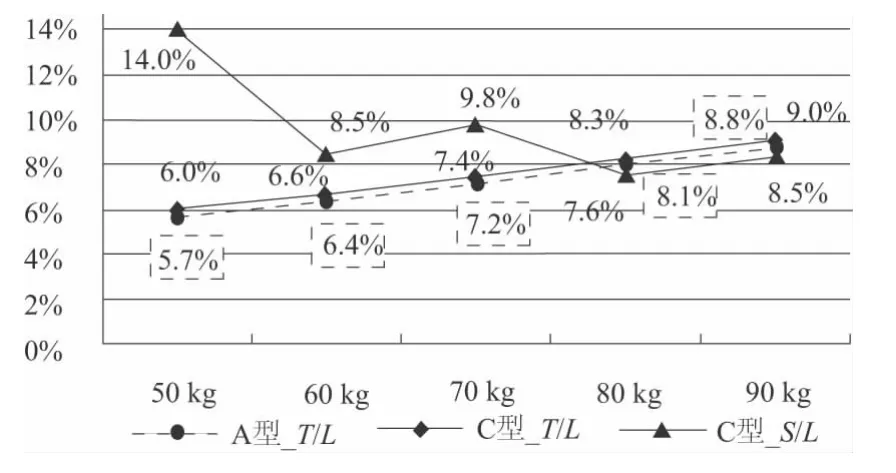
图5 最优尺寸比例T/L、S/L 曲线

根据图4、图5 中设计变量与元结构边长的比值曲线，最优尺寸比例D/L、T/L 和S/L 均随着质量的变化有较大变化。此外，A、C 两种型式元结构的最优尺寸比例D/L、T/L 并不相同。由此可得，用传统选型方法比较这两种型式的元结构时，采用统一D/L、T/L 会影响选型的正确性。

分析表1 中数据，元结构的前三阶频率均随着质量的增加而提高，因此，当备选的元结构质量相差较大时，比较结果并不可靠。表1 中数据显示，当质量约束条件相同时，优化后的元结构质量基本一致，A 型元结构前三阶频率加权和SUMFREQ 的值比C 型元结构略高，但C 型元结构的一、二阶频率则较A 型高。因此，从提高元结构低阶频率的目的出发，两型元结构的动态特性各有优点，动态性能相当。

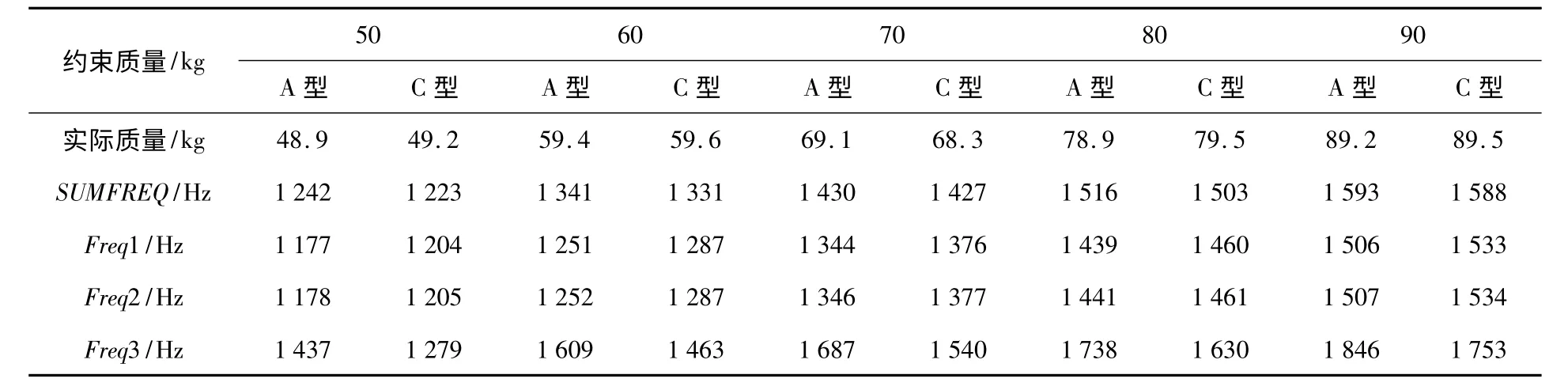
表1 优化后的元结构前三阶固有频率及实际质量

由上述分析可得以下结论:1)元结构的最优尺寸比例随着质量的变化而变化;2)元结构的质量和尺寸比例对其频率影响较大。未经优化的备选元结构质量不相同，同时尺寸比例有待优化。简单地通过比较由经验提出的元结构单体的频率选定元结构型式并不可靠。而借助ANSYS 对元结构进行尺寸优化，使备选元结构尺寸比例达到最优的同时，消除了质量差的影响，从而可在备选元结构质量基本一致的条件下，对其最优动态特性进行比较。

2.2 扩展结构间的分析比较

根据上述分析，就元结构单体而言，两种元结构动态性能相当。实际应用中，优化元结构的最终目的是提高由其扩展所得的床身等实际结构件的动态性能，因此，通过比较扩展结构的动态性能选定元结构型式更符合实际需要。以简单的长方体床身结构为例，将元结构扩展成3 ×2 ×2 个单元的扩展结构再进行分析和比较。选取优化后的元结构作为基本单元，分别进行扩展，扩展所得结构如图6 所示。

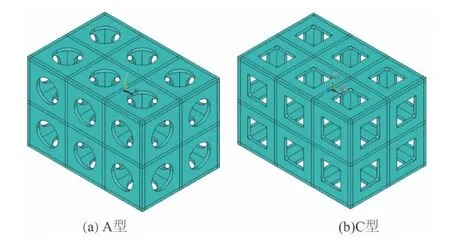
图6 扩展结构

对由不同质量的元结构扩展所得结构分别进行模态分析，得到扩展结构的前三阶固有频率和质量如表2 所示，表中Δ=(A－C)/C×100%。

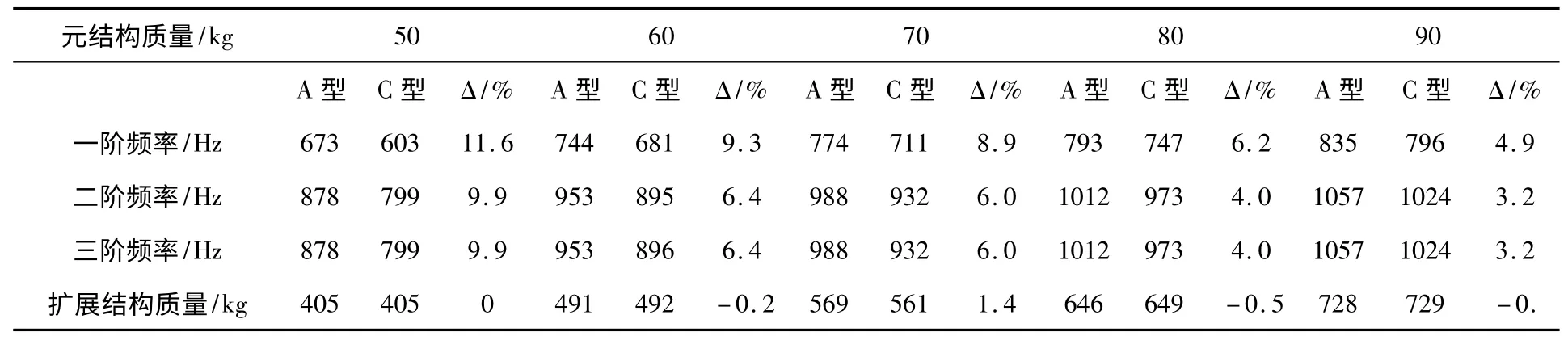
表2 扩展结构前三阶固有频率及质量

由表中数据可知:1)以同一质量的元结构进行扩展，扩展后两型结构实际质量基本一致，这是由于以上两种元结构的质量基本相等，且立方体元结构每个面完全相同，具有特殊性。一般情况下，由不同型式的元结构扩展所得结构的质量不相等，在注重控制结构质量的情况下，扩展结构的质量不可忽视;2)由同一质量元结构组成的扩展结构，A 型扩展结构的前三阶固有频率均高于C 型扩展结构，且平均高出6.6%。显然，就固有频率而言，A 型扩展结构的动态性能更优。

2.3 结果分析

根据前面的分析，就元结构单体间的比较而言，两种元结构的动态性能相当，而根据扩展结构间的比较，A 型扩展结构动态特性明显优于C 型。从优化实际结构整体动态性能的目的来看，由于扩展结构更接近实际结构，其动态性能更能反应整个结构的动态性能，即最优的扩展结构才是最终需要的。因此，本文提出的选型方法通过比较扩展结构来选择元结构的型式更符合实际，选型结果更准确。

3 结论

本文提出的元结构选型方法可有效解决目前选型方法存在的不足，其创新点在于:

1)应用ANSYS 优化模块先对备选元结构进行迭代优化，使元结构的动态性能均达到最优，同时可消除备选元结构间的质量差距，保证选型结果的可靠性。

2)将优化后的备选元结构进行扩展，分析、比较扩展结构的动态性能。分析表明根据扩展结构的动态性能选择元结构的型式更符合实际结构动态优化的需要。

元结构的选型过程即为先优化备选元结构，再将优化后的元结构扩展，最后根据扩展结构的动态性能选定元结构的型式。该方法使元结构的选型更准确，改进了元结构的选型过程，可以广泛应用于元结构的机床立柱、床身等复杂结构部件的动态优化，提高机床整机的动态性能。

［1］徐燕申，张兴朝，牛占文，等.基于元结构和框架优选的数控机床床身结构动态设计研究［J］.机械强度，2001，23(1):1-3.

［2］郭垒，张辉，汪劲松，等.元结构方法的理论建模和验证［J］.机械工程学报，2011，12(47)23:135-143.

［3］王宇奇.YK20100 磨齿机主要部件的有限元分析及结构优化设计［D］.长沙:中南大学，2009，48-49.

［4］朱军.高速立式加工中心模态分析及结构优化设计［D］.上海:上海交通大学，2009:51-52.

［5］张学玲，徐燕申，钟伟泓.基于有限元分析的数控机床床身结构动态优化设计方法研究［J］.机械强度，2005，27(3):353-357.

［6］张兴朝.基于有限元分析的模块化数控机床结构动态设计研究［D］.天津:天津大学，2001:36-37.

［7］王禹林，孙文钊，冯虎田.基于元结构的螺杆转子磨床床身动静态特性分析与优化［J］.振动与冲击，2012，31(16):183-187.

［8］张朝晖.ANSYS12.0 结构分析工程应用实例解析［M］.北京:机械工业出版社，2010:524-526.