基于尖点突变理论的大跨度巷道顶板稳定性分析
任智敏
(1. 山西煤炭职业技术学院,山西 太原 030031;2. 太原理工大学采矿工艺研究所,山西 太原 030024)
随着我国高产高效矿井的建设,大采高开采方法得到了大面积推广应用。为满足大型采掘运输设备和铺设风水管线的安装要求,正常生产、运输、通风及行人的安全规定,必然要求回采巷道跨度也随之扩大。但是,巷道跨度的增大会显著增加顶板的不稳定性,若支护不利,会出现顶板失稳情况。
相关物理试验及现场实践都表明巷顶板失稳具有突变性,表现为多因素影响下的非线性破坏[1]。目前有关基于突变理论的巷稳定性研究主要是根据总势能原理,建立了隧道失稳的尖点突变模型,导出了失稳的力学判据[2]。文献依据监测位移,基于突变理论,提出快速、简便评判围岩稳定的新方法和量化标准[3]。应用弹性稳定理论、非线性突变理论等研究了煤帮层裂结构的稳定性特征及突变失稳机制,得到了煤壁层裂结构的形成及屈曲失稳的规律[4]。基于突变理论分析了巷道围岩的变形和其工程力学属性,得出了围岩变形的稳定性判据[5]。根据突变级数理论,对影响地下工程围岩稳定性的因素进行多层次分解,对数据进行归一化处理,结合突变理论与模糊数学理论,进行综合量化运算,得到最后的评价类别[6]。目前关于大跨度回采巷道顶板稳定性的突变失稳研究不多,本文将采用尖点突变理论结合顶板组合梁理论对这一问题进行分析。
1 尖点突变理论
尖点突变理论研究的是多个参数变化时平衡点附近的状态分叉,即平衡点间的相互转换问题。突变是系统的整体性质,一般用表征系统全局性质的势函数来研究[7]。设势函数为最高4次幂函数,见式(1)。
V(y)=y4+∂1y2+α2y
(1)
在该系统中有一个变量y和两个控制参数α1和α2,从而可以构成三维空间。系统突变的约束条件见式(2)。
(2)
由式(2)可得系统的定态判别式(3)。
(3)
当Δ=0,系统为临界状态;Δ>0,系统为稳定状态;Δ<0,系统为非稳定状态。如图1所示,系统的定态y总是位于y、α1和α2构成的三维空间的平衡曲面上,或在平衡曲面的上叶,或在平衡曲面的下叶,因为中叶是不稳定的,不稳定的定态永远是不可到达的。平衡曲面的折痕在控制参数α1-α2平面上的投影就是突变点集,它是由形成尖点的两条曲线组成。定态y值几乎总是随控制参数α1和α2的变化而平稳变化,只有当控制参数α1、α2的取值越过曲线Δ=0时,y值才发生突变。对于最高幂次为y4的突变系统,不管控制参数有几个,其稳定或突变性质总等价于含有两参数α1和α2的系统。
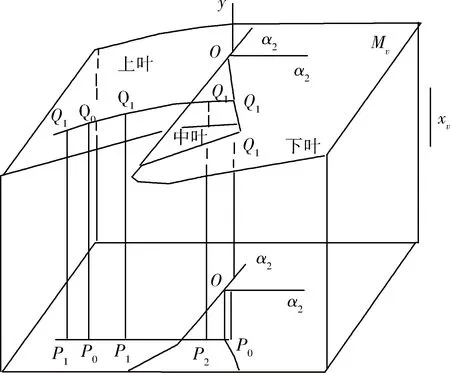
图1 尖点突变
2 巷顶板失稳的尖点突变模型
2.1 巷顶板受力变形的力学模型
将锚固后的顶板等效成一组组合梁,通过锚杆的轴向作用力将顶板各分层夹紧,以增强各分层间的摩擦作用,并借助锚杆自身的横向承载能力提高顶板各分层间的抗剪切强度以及层间粘结程度,使各分层在弯矩作用下发生整体弯曲变形,从而提高顶板的抗弯刚度及强度。
令巷道宽度为l,锚固范围内巷顶板受的垂直均布荷载q,水平荷载p。设弯曲变形发生在顶板组合梁的一个主惯性平面内,抗弯刚度为EI。距左支座为x处的截面挠度用ν表示,该截面上的弯矩见式(4)。
(4)
挠曲线近似微分方程见式(5)。
(5)
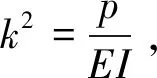
(6)
此微分方程的通解见式(7)。
实验组:Dixon术 48例、Miles术 3例、和Hartmann术 2例,切除率为100.00%,保肛率为90.57%;对照组:Dixon术 53例、Miles术 8例和Hartmann术 5例,切除率为92.96%,保肛率为74.65%。实验组切除率及保肛率均高于对照组,且差异具有统计学意义(P<0.05),见表2。
(7)
式中,A、B为积分常数,可利用边界条件x=0,ν=0;x=l,ν=0求得式(8)。
(8)
因此可得弯矩方程式(9)。
(9)
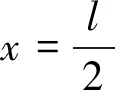
(10)
2.2 势函数的确定
巷道顶板在外力作用下发生变形所具有的变形能在数值上等于变形过程中外力所作的功。顶板弯曲变形时,横截面上既有弯矩又有剪力,因此应分别计算弯曲对应的弯曲变形能和剪切对应的剪切变形能。但对大跨度巷道的顶板,可等效成细长梁,剪切变形能很小,可忽略不计,因此只计算弯曲变形能。确定顶板的弯曲变形能为突变模型的势函数,见式(11)。
(11)
将式(9)代入式(11)中,积分得式(12)。
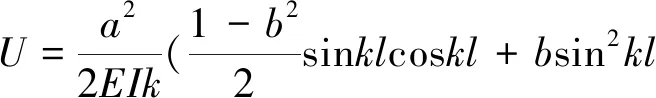
(12)
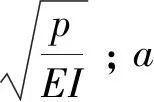
为方便分析,将式(12)中三角函数作4阶泰勒级数展开,并略去常数项, 得式(13)。
(13)
2.3 尖点突变模型的建立
(14)
由式(14)可知,突变模型的控制参数,见式(15)。
(15)
(16)
势函数在定态判别式上有退化的临界点,故对于整个力学模型系统而言,当Δ=0时,顶板处于稳定与非稳定的临界状态,见式(17)。
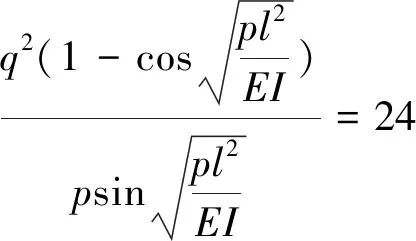
(17)
式(17)为巷道顶板失稳的判据,从式中看出,巷顶板失稳的临界状态取决巷道宽度l、巷顶板垂直压力q及巷顶板水平压力p的有机组合情况。
2.4 大跨度巷道顶板失稳的判据分析
根据巷道顶板失稳的判据得到影响巷道顶板失稳因素间的变化规律,如图2所示。从图2中可以看出以下3点。
1)图2中曲线表示巷顶板在巷宽、侧压及顶压共同作用下处于突变失稳时的临界状态,曲线上方区域表示巷顶板处于稳定状态,曲线下方区域表示巷顶板处于失稳状态。
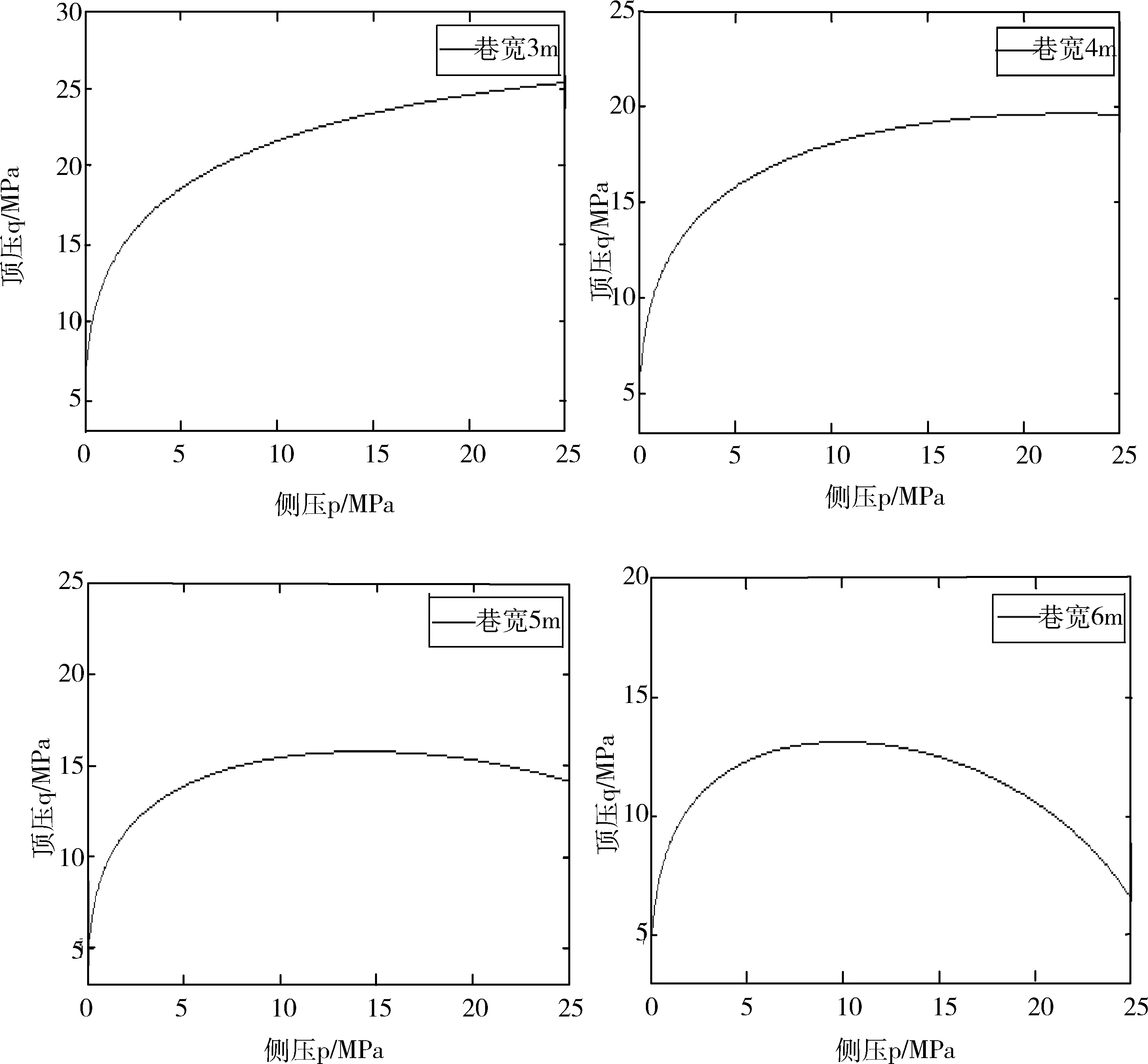
图2 巷顶板临界失稳影响因素间的关系
2)当巷顶板侧压p>5MPa时,巷宽越小,巷顶板在失稳时所能承受的顶压越大。当侧压p<5MPa时,巷宽度不论大小,巷顶板在失稳时所能承受的顶压基本相当。
3)对于巷宽l≥5m的大跨度巷道,顶压q=c(c为常数)的曲线与p-q曲线有两个焦点,说明侧压对大跨度巷道顶板稳定性影响显著,侧压较小或较大都可能引起顶板失稳。
3 结论
1)根据顶板的组合梁理论,结合尖点突变模型建立了判断巷顶板系统是否稳定的判据。判据表明,巷顶板失稳的临界状态取决巷道宽度l、巷顶板垂直应力q及水平应力p的组合情况。
2)顶板失稳判据曲线显示,在顶板侧压一定的情况下,随巷宽的增大,引起巷顶板突变失稳的顶压由大减小。当巷顶板侧压p>5MPa时,巷宽越小顶板越不容易突变失稳;当侧压p<5MPa时,巷宽对顶板的突变失稳影响不显著。
3)对于巷宽5m以上的大跨度巷道,随着侧压的增大,能引起顶板失稳的顶压先增大后减小,在顶压一定的情况下,顶板的稳定性对侧压的变化较敏感。
[1] Study on the Catastrophe Model of the Surrounding Rock and Simulating the Constructing Process by DEM in Gonghe Tunnel[C].The Institution of Engineering and Technology,2012.
[2] 祝云华,刘新荣,黄明,等.深埋隧道开挖围岩失稳突变模型研究[J].岩土力学,2009(3):805-809.
[3] 马莎,肖明.基于突变理论和监测位移的地下洞室稳定评判方法[J].岩石力学与工程学报,2010(S2):3812-3819.
[4] 秦昊.巷道围岩失稳机制及冲击矿压机理研究[D].徐州:中国矿业大学,2008.
[5] 王心飞.深埋隧道稳定性分析的智能化及非线性研究[D].重庆:重庆大学,2006.
[6] 付成华,陈胜宏.基于突变理论的地下工程洞室围岩失稳判据研究[J].岩土力学,2008(1):167-172.
[7] 谭云亮,刘传孝,赵同彬.岩石非线性动力学初论[M].北京:煤炭工业出版社,2007.

