基本上成立的概念及其应用

林谦， 杨祺

(1.云南师范大学 数学学院，云南 昆明 650092;2.云南农业大学 附属中学，云南 昆明 650000)

在实函中很多地方都涉及“基本上成立”的概念，如{xn}在(0,1)内处处收敛却不一致收敛，若从(0,1)内去掉一个长度为δ(0<δ<1)的小区间(1-δ,1)后，{xn}便在余下的点集(0,1-δ]上具有一致收敛性．一般地，当{fn(x)}在集合E(E⊂Rn)上不一致收敛时，仍有可能从E中去掉一个“很小”的e，使得{fn(x)}在余下的E-e上一致收敛[1]，但这样描述显得模糊、冗长且不够精确．因此，本文将用类似数学分析中极限的ε-δ定义给出“基本上成立”概念的精确定义，并探讨其性质．有了“基本上成立”的概念，便可简化许多定理及其证明的过程，同时使许多概念之间的关系显得更加简洁明了和协调．

1 基本概念

1.1 基本上成立的概念

定义1 设P(x)是一个与可测集E中的点x有关的命题，且∀δ>0，存在可测集Eδ⊂E，使得m(E-Eδ)<δ且命题P(x)在Eδ上成立，则称命题P(x)在可测集E上基本上成立，并将其记为P(x)n.*.成立于E，即P(x)n.*.成立于E∀δ>0，∃可测集Eδ⊂E，使得m(E-Eδ)<δ且P(x)在Eδ上成立，如易知函数列{xn}在E=(0,1)内基本上一致收敛于0．

1.2 函数列的几种收敛性概念

下面有关函数列收敛的各种详细概念见参考文献[2]，这里仅给出简述形式．

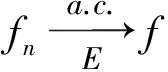
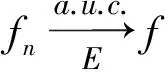
1.3 函数项级数的几种收敛性概念

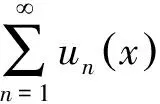
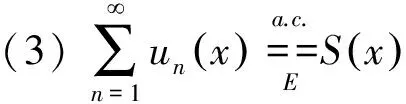
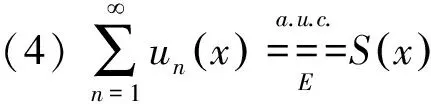
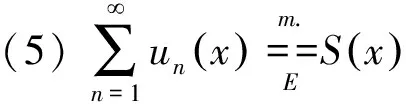
1.4 函数的几种连续性概念

(1)处处连续

定义3[3]若∀x0∈A(A⊂E)，f(x)关于点集E在点x0处连续，即∀x0∈A有

则称函数f(x)关于点集E在点集A上处处连续(简称f(x)关于E在A上连续)，或称函数f(x)关于点集E是点集A上的连续函数．

若记CE(A)={f(x)|f(x)关于E在A上连续}，则定义3可简述为：

f∈CE(A) ⟺ ∀

⟺ ∀x0∈A，f(x)关于E在点x0处连续．

下面有关函数连续的各种详细概念见参考文献[3]，这里仅给出简述形式．

1.5 函数的几种可导性概念

(1) 处处可导

定义4[4]若函数f(x)关于区域D(⊂Rn)在点集A(⊂D)上每一点处都可导(n>1时可导指对每个自变量的偏导数都存在)，则称f(x)关于区域D在点集A上处处可导(简称f(x)关于D在A上可导)，或称f(x)关于D是A上的可导函数．

若记DD(A)={f(x)│f(x)关于D在A上可导，则定义4可简述为：

f∈DD(D-E0)⟺ ∀x∈A，f(x)关于D在点x处可导．

(2) 几乎处处可导

⟺ ∃可测集E0⊂D，使得mE0=0且f(x)关于D在D-E0上可导．

(3) 基本上可导

⟺∀δ>0，∃开集Dδ⊂D，使得mDδ<δ且f(x)关于D-Dδ在D-Dδ上可导．

2 基本上一致收敛与其他收敛的关系

2.1 基本上一致收敛与一致收敛和几乎处处一致收敛的关系

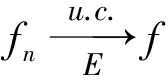
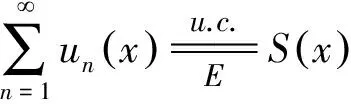
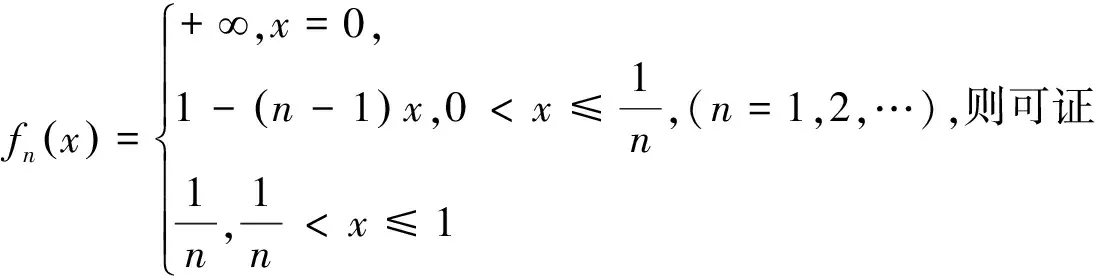
例1说明：对在E上基本上一致收敛的函数列{fn(x)}，即使mE<+，也不能保证函数列{fn(x)}在E上几乎处处一致收敛、一致收敛和处处收敛．

2.2 基本上一致收敛与基本上收敛的关系

推论2[2]若mE<+，则

推论4 若mE<+，则

2.3 基本上一致收敛与几乎处处收敛的关系

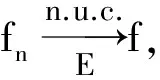
推论5[2]若mE<+，则

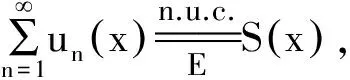
推论7 若mE<+，则

2.4 基本上一致收敛与处处收敛的关系

定理4[2]若mE<+且则反之不成立(见例1)．

推论8 若mE<+且则反之不成立．

2.5 基本上一致收敛与度量收敛的关系

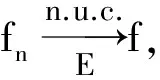
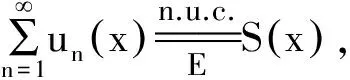
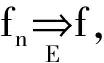
注：在推论2、推论4、推论5、推论7的充分条件中不需假设mE<+.

3 基本上收敛与其他收敛的关系

下面所涉及的函数均为可测集E上几乎处处有限的可测函数，不再赘述．

3.1基本上收敛与几乎处处收敛的关系

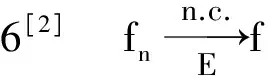
3.2 基本上收敛与基本上一致收敛的关系

见定理2、推论2、推论3和推论4．

例3(叶果洛夫定理)[2]若mE<+且则

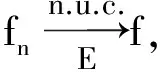
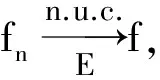
3.3 基本上收敛与度量收敛的关系

定理7[2]若mE<+且则反之不成立(见例6)．

推论11 若mE<+且则反之不成立．

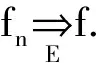
例6说明：对在E上度量收敛的函数列{fn(x)}，即使mE<+，也不能保证函数列{fn(x)}在E上基本上一致收敛、几乎处处一致收敛、一致收敛、基本上收敛、几乎处处收敛和处处收敛，由此进一步说明度量收敛的函数列是各种收敛函数列中收敛性最弱的一种情形．

例7 若mE<+且则∃{fnk}⊂{fn}，使得

证明因mE<+且故由定理2有从而结合定理5和黎斯定理便得证．证毕

4 基本上连续与可测函数的关系

定理8(鲁金定理)[5]若f(x)是可测集E上的几乎处处有限的可测函数，则∀δ>0，∃闭集Fδ⊂E，使得m(E-Eδ)<δ且f∈CFδ(Fδ)，即f(x)关于E在E上基本上连续．

推论12 若f(x)是可测集E上的几乎处处有限的可测函数，则f(x)关于E在E上基本上连续，且∀δ>0，∃闭集Fδ⊂E及g∈CRn(Rn)，使得f(x)=g(x)于Fδ及mE[f≠g]<δ.

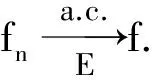
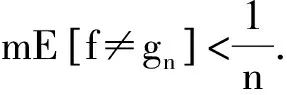
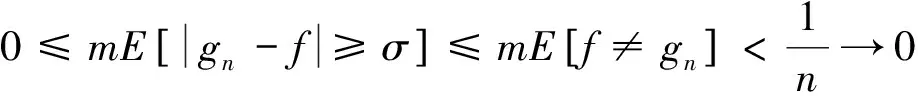
5 基本上连续与其他连续的关系

由定义容易看出，当函数f(x)关于点集E在E上处处连续且A⊂E时，函数f(x)关于点集E在A上也处处连续，但反之不成立．由此有：

5.1 基本上连续与处处连续的关系

定理9[3]若f∈CE(E)，则f(x)关于E在E上基本上连续，即∀δ>0，∃可测集Eδ⊂E，使得mEδ<δ且f∈CE-Eδ(E-Eδ)，反之不成立(见例9)．

5.2 基本上连续与几乎处处连续的关系

定理10[3]若函数f(x)关于E在E上几乎处处连续，则f(x)关于E在E上基本上连续，反之不成立(见例9)．

5.3 基本上连续与本性连续的关系

定理11[3]若函数f(x)关于E在E上本性连续，则f(x)关于E在E上基本上连续，反之不成立．

例10 对E=[0,1]，用类似于Cantor集的构造法可构造一个无内点的闭集A⊂E，使得mA>0且0,1∈A，则可在E上定义可测函数

f(x)=χA(x)(点集A的特征函数)

于是由鲁金定理知，函数f(x)关于点集E在E上基本上连续，且可证[3]函数f(x)关于点集E在E上非本性连续．

6 基本上可导与其他可导的关系

6.1 基本上可导与处处可导的关系

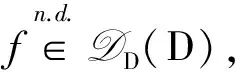
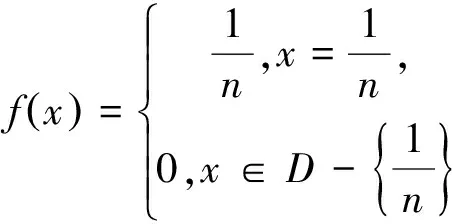
6.2 基本上可导与几乎处处可导的关系

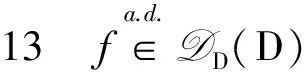
证明“⟹” 由定义立得．

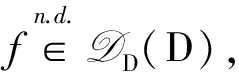
[1] 江泽坚，吴智泉，纪友清．实变函数论[M]．三版.北京：高等教育出版社，2007．

[2] 林谦．关于可测函数列的各种收敛性[J]．云南师范大学学报：自然科学版，1994，14(1)：8-17．

[3] 林谦．函数在点集E⊂Rn上连续的六个层次[J].云南师范大学学报：自然科学版，2002，22(4)：4-7.

[4] 华东师范大学数学系编．数学分析[M]．四版.北京：高等教育出版社，2010．

[5] 程其襄，张奠宙，魏国强，等．实变函数与泛函分析基础[M]．三版.北京：高等教育出版社，2010．