竞争环境下的M/M/1休假排队服务策略研究
侯晓燕, 李继红
(1.山西大学 数学科学学院,山西 太原 030006;2.山西大学 经济与管理学院,山西 太原 030006)
引 言
随着电子商务和现代技术的迅猛发展,管理机构和通讯网络的运行越来越复杂,顾客对服务质量和系统性能的要求也越来越高,而排队服务是优化服务机构行为的一种有效方法.基于此,优化服务系统广泛应用于生活中,如公交车站停靠优化[1]、收费站设计与管理[2]和通信服务台资源管理[3]等,企业通过研究顾客的行为来调整排队系统的服务机制,从而得到平衡性策略.Hassin和Haviv[4]研究了排队系统中顾客的行为及排队均衡策略.Stidham[5]对M/M/1排队系统中的顾客行为和服务机制作了优化.在此基础上,孙霞林等[6]对排队服务系统进行了分析,给出了统计平衡条件的主要指标,讨论了该排队系统的最优化问题.另外一些文献基于服务时间竞争研究了经济排队模型,Brill和Hlynka[7]、Christ[8]研究了以等待时间来竞争顾客的问题.Kut[9]在寻找最优价格和等待时间过程中,得出了不同的企业和市场特点将影响企业产品的价格和顾客的等待时间.Parra-Frutos[10]在不确定环境下,研究了以时间竞争的M/M/1排队模型,去寻找使企业利润最大化的等待时间和服务能力水平,但也仅是采用数据处理的方式给出了分析结果,并未实际建立模型且给出理论结果;并且,当系统中没有顾客,服务台就会处于休假状态,从而影响了顾客的逗留时间;这种休假排队在实际生活中得到很多应用,如计算机系统、通信网络、生产制造系统[11-12].还有一类研究考察了存在第二种服务可选的M/M/1排队模型[13-14].但目前的研究很少将休假机制与排队平衡性策略结合考虑,基于此,在完全竞争假设下,本文不仅要研究使企业利润最大化的服务行为,还要研究休假排队的顾客行为,提出了以时间竞争的休假排队服务模型,目的是寻找排队最优指标,比如服务能力、等待时间、价格、输出率等.
1 模型假设
由于顾客必须等待一定的时间才能获得服务,其中产品价格p>0,所以顾客不仅对价格感兴趣,而且对等待时间成本感兴趣.将价格和等待时间成本的和称为总费用.假设条件
p+cW≤R
(1)
其中c是每个顾客等待的单位时间成本,W为顾客的期望等待时间,R是顾客被服务后所得的收益.只要顾客所花的总费用不超过服务所得的收益,顾客就愿意来接受服务.
设顾客到达过程服从参数λ的泊松过程,且假设其对价格和等待时间敏感,所以到达率λ是关于价格和期望等待时间的函数,即:
λ=λ(p,W(μ))
(2)
在完全竞争假设下,存在许多的服务企业和顾客,产品都是相同的.考虑M/M/1排队模型,企业的服务是参数为μ的泊松过程,当系统中没有顾客时,服务台立即进入休假,休假时间服从参数为θ的指数分布,从而影响了顾客的等待时间.期望等待时间(排队时间加上服务时间)表达式为
(3)
在排队系统M/M/1中,输入与输出相同,且不被服务机制所影响,所以,若到达过程为参数λ的泊松过程,则输出过程也是参数λ的泊松过程.
2 期望利润函数
假设给定期望等待时间,参数c和R已知,将得到满足表达式(1)的产品价格.因此,为了得到最优的价格,需要最优的期望等待时间.
假设将企业成本建立在服务能力和到达率上:建立在服务能力上的成本函数表示为C(μ),即服务顾客的能力,假设当μ≠0时,C(μ)≠0,dC(μ)/dμ=C'(μ)>0,并且它是连续可导的,它的一阶导数和二阶导数都是连续的;建立在到达率上的成本表示为γ,是每个顾客的固定成本.
由于本文考虑的是休假排队模型,所以到达率还是关于休假能力θ的函数,由(3)式可以得到到达率λ的函数为:
(4)
由(1)式可得价格p的函数为:
p(W)=R-cW
(5)
期望收入函数为:I(W,μ,θ)=λ(W,μ,θ)[p(W)-γ]
因此,期望利润函数为:
π(W,μ,θ) =期望收入-服务能力=I(W,μ,θ)-C(μ)
式中W、μ和θ均为变量.
为保证利润函数有意义,企业的收入必须为正,否则,企业将不会设定这样一个方案.由此得到以下条件:

此条件使得λ和p(W)-γ都为正,从而保证了期望收入为正.
条件B 由条件A可得1/μ+1/θ<(R-γ)/c,所以服务能力μ必须满足如下条件:
此条件给出了服务能力的可能取值范围,表示如果条件A成立的话,那么条件B也成立,反之不成立.为了简化,将最小的服务能力cθ/[(R-γ)θ-c]表示为μ*.
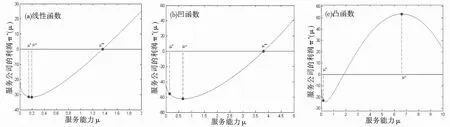
条件C 由条件A可得1/μ+1/θ<(R-γ)/c和1/μ+1/θ 同样,条件A成立,条件C成立.将最小休假能力max {μ/(Wμ-1),cμ/[(R-γ)μ-c]}称为θ*. 条件D 服务能力成本函数C(μ)是这样一个函数:存在使得期望利润函数为正的W、μ和θ. 因此,企业期望利润函数可以写成如下: (6) 在这里,条件A、B和C已包含.在研究利润最大化的解决方案之前,先来研究此函数的一些性质. 引理1 期望利润函数π(W,μ,θ)有以下性质: (i) 当W>1/θ时,π(W,μ,θ)关于W是严格凹函数; (ii) 存在两个值W1、W2,使得1/μ+1/θ (iii) 当W∈(1/μ+1/θ,(R-γ)/c)时,π(W,μ,θ)存在最大值; (iv) 当0 (v) 当0 证明(i)π(W,μ,θ)关于W的一阶导数和二阶导数为: (7) 当W>1/θ时,容易看出上式恒小于0.因此π(W,μ,θ)对∀W>1/θ是严格凹函数; (ii) 因为当W=1/μ+1/θ和W=(R-γ)/c时,π(W,μ,θ)<0,再由条件A和D可知,存在一个开区间(W1,W2)⊂(1/μ+1/θ,(R-γ)/c)使得π(W,μ,θ)为正,且π(W1,μ,θ)=π(W2,μ,θ)=0; (iv)π(W,μ,θ)对μ求一阶导数和二阶导数: 容易看出结论成立; (v)π(W,μ,θ)对θ求一阶导数得: 由p-γ>0可知上式恒大于0.因此,π(W,μ,θ)关于θ>θ*是严格递增的. 在给定服务能力和休假能力的前提下,要得到企业的最优方案,需要利润最大化的等待时间.因此,有如下定理: 定理1 在完全竞争假设下,以时间竞争的M/M/1休假排队服务企业,到达率由收益为R、等待时间成本为c的顾客组成.给定服务能力μI>μ*,休假能力θI>θ*,则企业的最优等待时间为: (8) 企业的最优产品价格为: (9) 企业的最优输出率为: (10) 证明由引理1中的性质(iii)可知期望利润函数(6)式在区间(1/μ+1/θ,(R-γ)/c)上存在一个最大值.因此利润最大化的等待时间就是令(7)式等于0,即可得到(8)式.很容易得到(9)、(10)式. 这样,顾客就可根据企业的服务能力和休假能力来调整顾客的到达过程,同时,企业可设定出合理的价格. 由最优等待时间的表达式得到了利润函数,记为π*(μ),下面用此函数去寻找最优的服务能力水平. 将(8)式代入(6)式可以得到利润函数π*(μ): (11) 可以看出π*(μ*)=-C(μ*)<0. 使得(11)式最大化的条件一为: (12) 在这里,μ~是否存在关键在于C(μ),如果μ~存在,也没有明确的表达式.条件二为: (13) 此研究中的μ~如果存在的话,有如下引理: 引理2 如果μ~存在,那么μ~>μ*. 证明由于C′(μ)>0,再由(12)式有 因此, 观察(13)式,π*(μ)为凸函数或为凹函数关键在于服务能力成本函数C(μ)的情形.因此,有如下结论:服务能力成本函数C(μ)不同,服务能力μ对利润函数π*(μ)的影响也不同.特别地,我们分别讨论C(μ)为线性函数、凹函数和凸函数的情况,即C″(μ)=0、C″(μ)<0和C″(μ)>0. 引理3 如果C(μ)为线性函数或凹函数,则π*(μ)为凸函数,如果最小值μ~存在,有π*(μ*)<0,如果最小值μ~不存在,π*(μ)随着μ的增加而增加. 证明如果C(μ)为线性函数,则C″(μ)=0,(13)式大于0,π*(μ)为凸函数.如果C(μ)为凹函数,则C″(μ)<0,(13)式大于0,π*(μ)也为凸函数.如果μ~存在,由于π*(μ*)<0,又μ~为最小值,所以π*(μ~)<π*(μ*)<0.如果μ~不存在,由于π*(μ*)<0并且由条件D知存在使得π*(μ)>0的μ,所以π*(μ)关于μ是严格递增的. 因此,如果C(μ)为线性函数或凹函数,服务企业的最优方案有如下定理: 定理2 如果C(μ)为线性函数或凹函数,则存在一个服务能力水平μ**,μ**>μ*,π*(μ**)=0,当μ>μ**时,π*(μ)>0,且随着的μ增加而增加. 因此,如果C(μ)为线性函数或凹函数时,不存在使得企业利润最大化的服务能力水平,它的利润随着服务能力的增加而增加. 引理4 如果C(μ)为凸函数时,π*(μ)先是凸函数,随着μ的增加,π*(μ)变为凹函数.另外,最小值(最大值)在凸(凹)区间取到. 综合以上结果,并且考虑到π*(μ*)<0,有如下的推论: 推论1 如果C(μ)为凸函数,π*(μ)的最优解在凹区间取得. 因此,由定理2和推论1能够得到如下结论: (1)当服务能力成本函数是线性函数或凹函数时,企业的利润随着服务能力的增加而增加,此时,企业不存在最优方案; (2)当服务能力成本函数是凸函数时,企业存在最优的服务能力. 假设c=10,R=100,γ=10,给定休假能力θI=1/2,将其代入(11)式来验证企业利润与服务能力的关系. 当服务能力成本函数为线性函数,并设C(μ)=10μ+30时,如图1(a)所示.从图中可以看出,极值μ~存在,且μ*<μ~,与引理2相符.存在μ**使得π*(μ**)=0,并且,当μ>μ**时,π*(μ)>0,且随着μ的增加而增加,同定理2.因此,没有最优的服务能力. 当服务能力成本函数为凹函数,并设为C(μ)=-2μ2+40μ+50时,如图1(b)所示.从图中可以看出,极值μ~存在,且μ*<μ~,与引理2相符.存在μ**使得π*(μ**)=0,并且,当μ>μ**时,π*(μ)>0,且随着μ的增加而增加,同定理2.同样没有最优的服务能力. 当服务能力成本函数为凸函数,并设为C(μ)=3μ2-40μ+20时,如图1(c)三所示.从图中可以看出,在μ~处取得最大值,此时企业的利润最大,同推论1.此时,存在最优的服务能力. 图1 不同服务成本函数(a)线性函数,(b)凹函数,(c)凸函数下公司利润与服务能力的关系 研究了完全竞争环境下,以时间竞争的休假排队服务企业的平衡性策略.本文建立的模型得出了服务企业的最优策略必须随服务能力成本函数的变化而变化.因此,在确定的环境下,以时间竞争的企业,加快工作进程不一定总是带来越高的利润. [1] 林培群,徐建闽.BRT车站组停靠线路组合优化问题的建模求解与仿真[J].系统工程理论与实践,2012,32(11):2570-2576. [2] 潘全如,朱翼隽.排队论在收费站设计与管理中的应用[J].运筹学学报,2009,13(3):95-102. [3] 戴琳,秦叔明,董艳梅.切换排队且排队优先的通信信道配置模型[J].云南师范大学学报:自然科学版,2012,32(2):42-46. [4] HASSIN R,HAVIV M.To queue or not to queue:equilibrium behavior in queueing systems[M].Boston:Kluwer Academic Publishers,2003. [5]STIDHAM S JR.Optimal design of queueing systems[M].Boca Raton:CRC Press,Talyor and Francis Group,2009. [6] 孙霞林,曾华,熊德之,等.基于排队的服务系统的最小成本[J].武汉工程大学学报,2008,30(1):125-126. [7] BRILL P H,HLYNKA M.An exponential queue with competition for service[J].European Journal of Operational Research,2000,126(3):587-602. [8] CHRIST D,AVI-ITZHAK B.Strategic equilibrium for a pair of competing servers with convex cost and balking[J].Management Science,2002,48(6):813-820. [9] KUT CSO.Price and time competition for service delivery[J].Manufacturing & Service Operations Management,2000,2(4):392-409. [10]PARRA-FRUTOS I.A queuing-based model for optimal dimension of service firms[J].SERIEs,2010,1:459-474. [11]DOSHI B T.Single server queues with vacations[J].In:Takagi H(Ed.).Stochastic Analysis of the Computer and Communication Systems.Amsterdam:North-Holland Elsevier,1990:217-264. [12]TIAN N,ZHANG G Z.Vacation queueing models-theory and applications[J].New York:Springer-Verlag,2006. [13]阿力木·米吉提,蔡玲霞.第二种服务可选的M/M/1排队模型状志空间及对偶空间的完备性[J].新疆师范大学学报:自然科学版,2012,31(2):72-76. [14]仲彦军.有两个服务阶段、反馈、强占型的M/M/1重试排队模型的一个特征值[J].新疆师范大学学报:自然科学版,2013,32(1):37-42.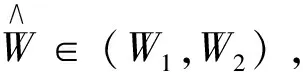
3 最优方案的设定
3.1 期望等待时间
3.2 最优服务策略
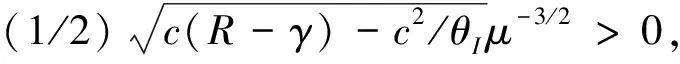
4 实例分析
5 结 论
——国外课堂互动等待时间研究的现状与启示

