三角网格顶点重要度的自适应Loop细分算法

王艳艳，惠丽峰，罗晓锋，张荣国

1.内蒙古科技大学高等职业技术学院，内蒙古包头014010

2.内蒙古科技大学矿业工程学院，内蒙古包头014010

3.太原科技大学计算机学院，太原030024

1 引言

在CG、几何造型等领域中，物体表面通常是用三角形网格模型来描述的。在多数情况下，需要使用三维激光扫描仪对大物体、宽场景进行数据采集。为了适应计算机对这些数据的实时显示、传输、分析、编辑、重建、存储等要求，必须对这类模型数据进行处理。一类是简化网格模型：在保持物体特征和视觉效果的前提下，减少该模型的顶点数、边数、三角面片数；另一类是自适应细分：通过控制误差来局部细分网格，力求以较少的网格来获得性能良好的曲面。对三角网格进行简化和细分是CG研究领域的两大热点。

经过多年的发展，细分算法已经成为图形学领域的一种标准造型技术。现有的细分模式有：Loop[1]、Catmull、Clark[2]、3[3]、混合细分[4]模式等，文献[5]提出了一种广泛的Loop细分方法。自适应细分算法是传统细分算法的一种改进，它主要研究如何确定自适应细分准则，消除裂缝以及修正顶点几何属性等。对于这些问题的解决，国外Ashish Am resh等人对三角网格自适应细分[6]作了探索，文献[7]提出了一种增量自适应细分，该方法可以根据用户的需求只对选定的区域进行细分；国内有华中科技大学的胡等对四边形的自适应细分[8]作了研究；另外，文献[9-11]也在自适应细分方面作了大量的研究。

到目前为止，很多三角形网格的自适应细分方法[5，10-14]已被提出，但这些算法都不可避免会产生一些退化三角形，使得部分面片处于不同层，破坏了整体细分曲面的连续性。本文将域平均平面的距离[15]作为尺度，并根据文献[16]求平均平面网格简化方法中常用到的顶点重要度作为判断顶点是否参与细分的标准，用顶点到其1-邻的方法对其进行改进。经过大量的实验发现，该方法计算简单，处理速度快，其时间性能优于其他算法。

2 Loop细分模式

它是一种基于三角网格1-4面分裂的、逼近的细分模式，生成的曲面是盒式样条曲面的推广，在正则曲面上是C2连续，在奇异点处是C1连续。

此细分模式的各种顶点细分模板如图1所示。

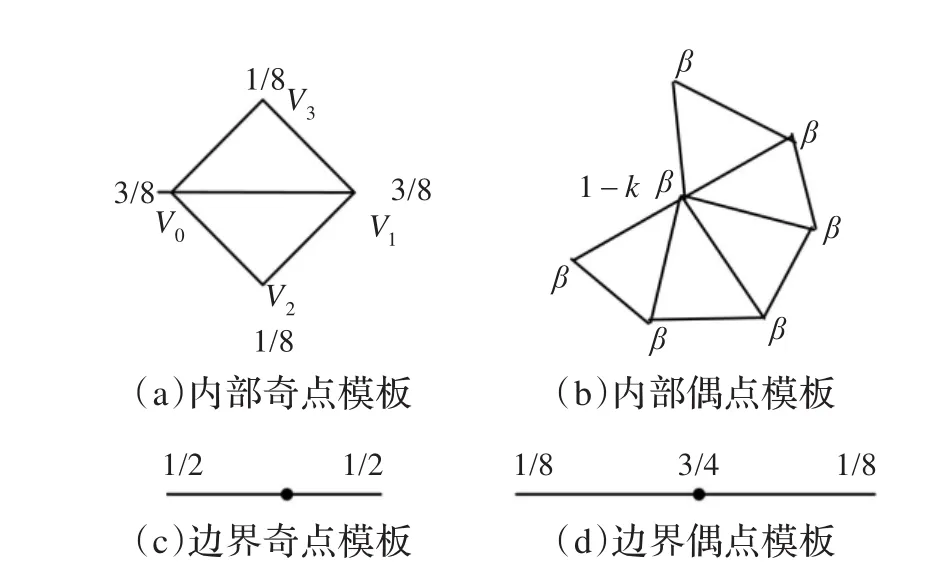
图1 Loop细分模板示意图

（1）内部奇顶点的计算公式为：

（2）内部偶顶点的计算公式为：

设V0，V1，…，Vk-1是顶点V的1-邻接顶，k为顶点V的价，β的定义如下：

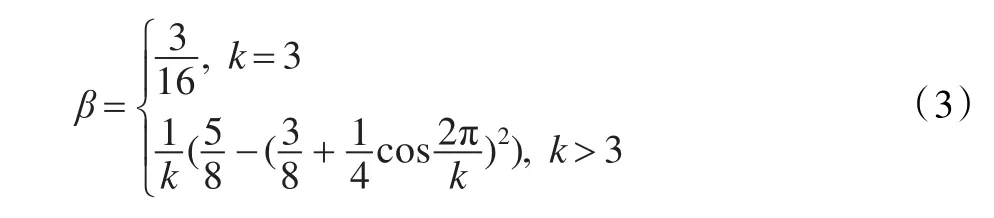
（3）边界奇、偶顶点，可分别用图1（c）、（d）的模板来计算。

3 新的自适应细分算法

经过大量实验发现，对空间网格形状影响越大的顶点越容易被细分，对网格形状影响越小的顶点就越不容易被细分。本文以顶点到其平均平面的距离作为细分准则，这样顶点细分就转换为判断顶点重要度的问题了。

定义1 （顶点的星型域）在空间三角形网格中，把顶点V（内点）和其1-邻域上的顶点构成的封闭区域称为V的星型邻域，记为Star(V)。对于点V为边界点的情况，称由V，V1，V2，…，Vi组成的三角形区域为点V的半星型邻域Starhalf(V)，将V的星型邻域和半星型邻域统称为Star(V)。

定义2 （平均平面）对于顶点V的星型邻域，必存在一个平面，使得点V的所有邻域点Vi到此平面的距离和最小，则称它为Star(V)的平均平面，记为SStar(V)。

3.1 顶点重要度的改进

根据定义可知，顶点V的平均平面是存在的，但要将这个平面表示出来是非常困难的。鉴于此，计算顶点到其平均平面的距离时，用与此顶点相连较长三条边的端点构成的平面来代替平均平面，因而顶点的重要度得以改进。

3.1.1 平均平面

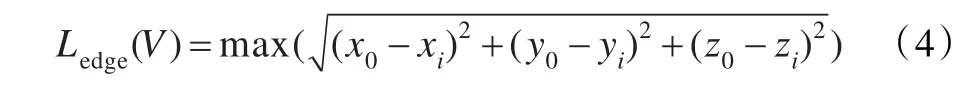
设(x0，y0，z0)为顶点V的坐标，(xi，yi，zi)为顶点V的1-邻域上所有点的坐标。利用公式（4）求出三条最长边的端点Vi、Vj、Vk，已知它们坐标(xi，yi，zi)，(xj，yj，zj)，(xk，yk，zk)，利用这三个点的坐标可得平面的三点式方程：

将公式（5）转化为平面的一般方程为：Amx+Bmy+Cmz+Dm=0，即为平均平面方程。

3.1.2 顶点的重要度

网格模型上的点可分为内部顶点和边界顶点，它们的重要度与该点在空间网格上的曲率相对应，曲率越大，对空间网格形状的保持就越重要，这样的顶点也就越容易细分；否则，反之。

内部点的重要度可定义为顶点V(x0，y0，z0)到平均平面Amx+Bmy+Cmz+Dm=0的距离，如图2所示。记为Degree(V)，当顶点V的星型邻域上点确定时，DVS的值越大，相应顶点V处的曲率变化也越大。

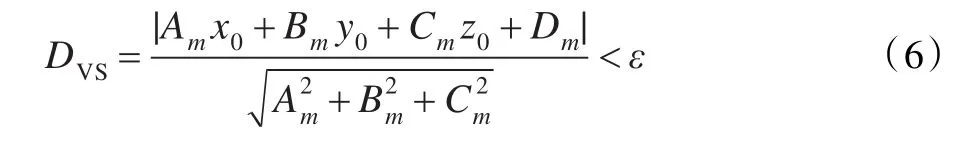
图2 内部顶点V的重要度

由于边界顶点位置决定了边界的形状，因此其重要度不仅与边界顶点处的曲率有关，还与其所在的边界曲线的曲率有关。设V1、Vi为边界顶点V的半星型邻域上的两个边界顶点，V2、V3、V4，为这个邻域上的内部顶点。V点周围顶点所确定的平均平面为SStar(V)，DVS为点V到平面SStar(V)的距离，DVE为点V到边界线V1Vi的距离，如图3所示。

图3 边界顶点V的重要度

边界线V1Vi直线方程为：

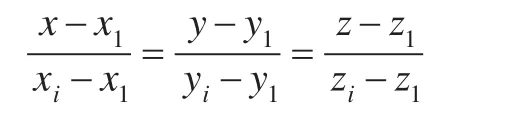
那么顶点V(x0，y0，z0)到此直线的距离[17]为：

其中ni=(Ai，Bi，Ci)，i∈n，M=A1x0+B1y0+C1z0+D1，N=Aix0+Biy0+Ciz0+Di。根据公式（6）、（7），边界顶点的重要度就为：

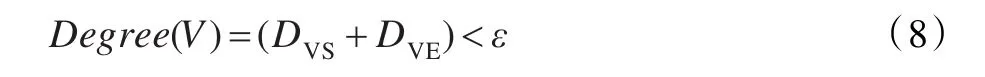
上述的改进方法会造成一定程度的误差，但误差可限制在为数不多的三角形范围内。对数据源密度非常高的网格模型来说，对应的三角面片非常小。本文的细分方法可以在一定程度上减少对最终显示效果影响不大的冗余计算，重点突显三维图形的主要特征和拓扑结构，适宜对显示速度有较高要求的情景。

3.2 算法步骤

为了清晰地说明本文算法，先来定义三对名词。假设三角网格中的某个顶点的重要度小于给定的阈值，则此点为死点，反之为活点；只有当三角形一条边上的两个点都为死点时，该边才为死边，其余均为活边；当一个三角形至少有两条死边时，这个三角形为死面，其余为活面。本文算法的具体步骤为：

（1）遍历全部顶点，计算各个顶点的价。

（2）依据公式（6）或公式（8）计算出每个顶点的重要度，如果Degree(V)小于给定的阈值ε，则记为死点。

（3）由三角形所含死点的个数，确定三角形的边的类型和面的类型。

（4）新（奇）点的生成。在活边上按照Loop细分模式插入新点，采用Loop细分模板计算其插入位置。死边上就不需要插入新点。

（5）新面的生成。对死面不进行分裂生成新面。活面的分裂方式又分为两种：

①当三条边都为活边时，将该面分裂成4个小三角形；

②当只有一条死边时，死边上不插入新点。另外两条边顶点处重要度决定了新的三角形生成方式。

（6）采用Loop细分模板更新所有偶点的位置。

（7）判断是否进行下次细分，直到满足需求。

4 实验结果和分析

为了验证本文算法的有效性，利用C++和OPENGL图形函数库，在VC++6.0环境编程实现了相应算法，对原始面片数为914的汽车模型、面片数为3 121的人体模型及面片数为8 516地形模型进行了三次细分，如图4～6所示。

图4 汽车模型自适应细分结果图

从图4～6可以看出，本文算法主要集中在对高曲率部分进行细分，汽车模型中，特别是对车轮和车体具有棱边、棱角等具有尖锐特征的部位细分得最多；车窗、车顶和车门等平坦的部位细分较少。人体模型中，对脖颈截面、双乳及肚脐部分细分较多，其他部分较少；地形模型中，对山脊部分细分多，而平地部分细分少。将本文算法和文献[8]中的算法进行了实验比较，表1在给定同一阈值的情况下对这两种方法的实验结果作了统计。

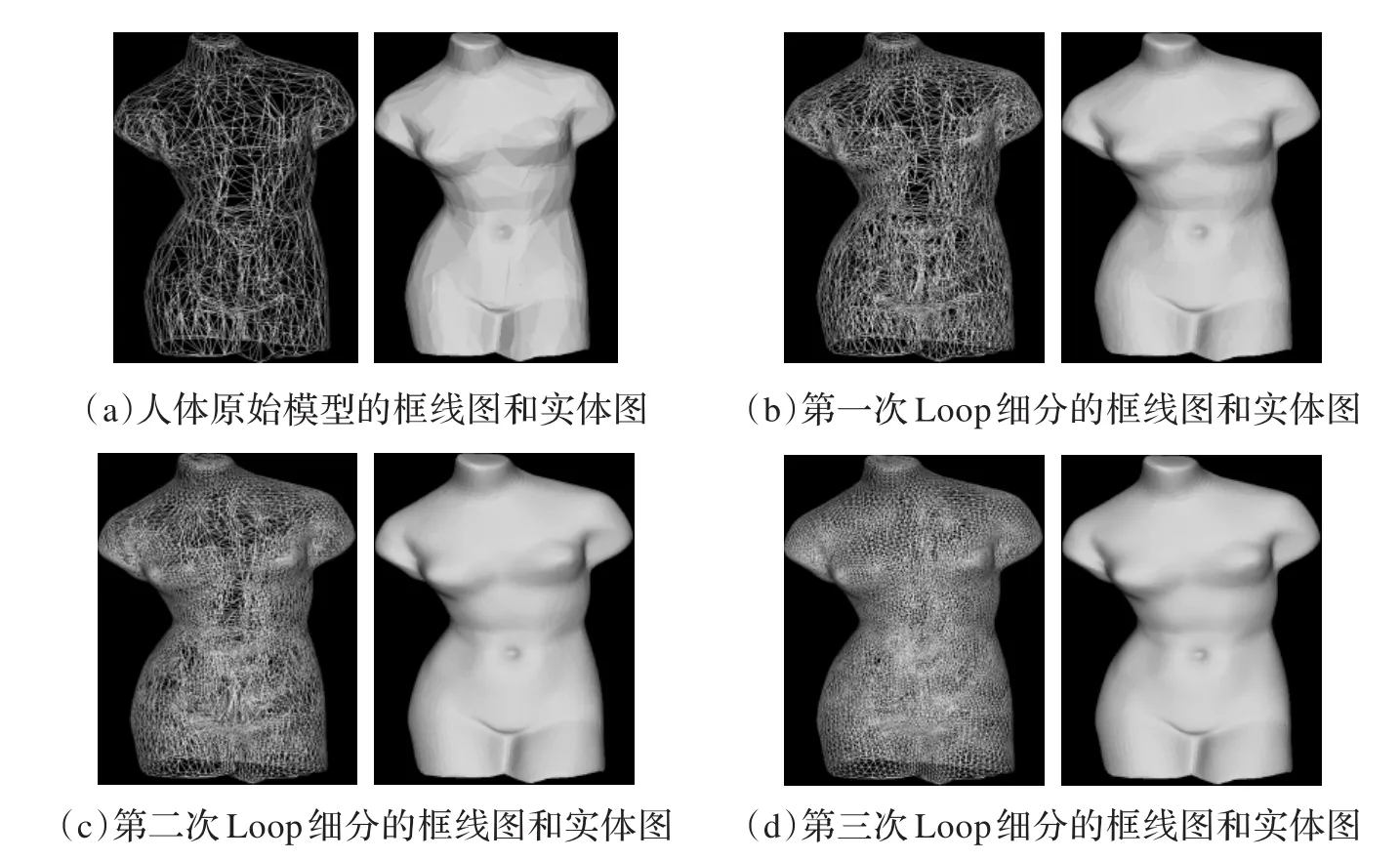
图5 人体模型自适应细分结果图

图6 地形模型自适应细分结果图

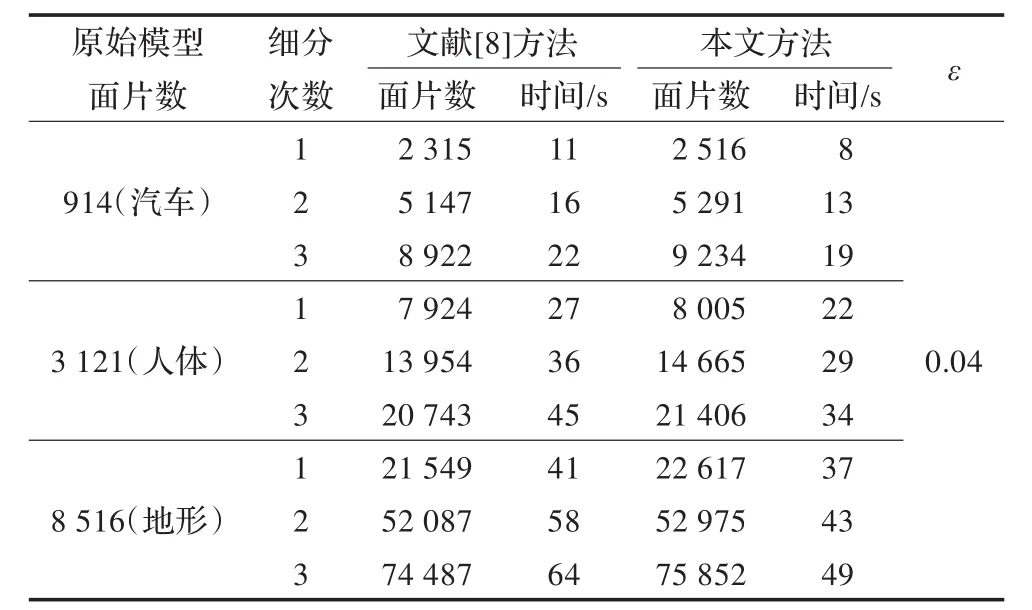
表1 两种方法的实验结果对比

通过表1可以看出，本文算法在三次细分过程中产生的三角面片数都要多于文献[8]中的算法，但是随着细分次数增多，三角面片数的增加，本文算法的时效性就越发地显现出来，这是因为本文算法通过距离来判定顶点是否参与细分，省去了反复计算顶点法矢的过程，加快了对数据量非常庞大的模型进行处理，时间效率比较高。

5 结论

以与顶点相连较长三条边的端点构成的平面近似为该顶点的平均平面，这与用网格面积法向加权求得的平均平面相比，前者就存在着很大的误差。但目前三角网格模型的数据量都越来越庞大，精度也越来越高，在这样的网格模型中，三角形的面积非常小，密度高且各三角形的形状也比较接近，因此该方法产生的误差可被限制在一定数量的三角形之内，对最终简化结果的视觉影响不大，是可以采用的。以距离作为细分尺度，省去了反复计算三角形法矢量和面积的过程，大大减少了庞大数据模型的计算量，时间优越性能很高，但是细分后的三角面片数较多，这是本文算法的不足之处。以后的主要工作将集中在保持良好的细分效果情况下，既有高的时效性，又能最大化减少三角面片数。

[1]Loop C.Smooth subdivision surfaces based on triangles[D].Utah,USA:University of Utah，1987.

[2]Catmull E，Clark J.Recursively generated B-spline surfaces on arbitrary topological meshes[J].Computer Aided Design，1998，l0（6）：183-188.

[3]Doo D，Sabin M.Behaviour of recursive division surfaces near extraordinary points[J].Computer Aided Design，1978，10：356-360.

[4]Stam J，Loop C.Quad/triangle subdivision[J].Computer Graphics Forum，2003，22（1）：79-85.

[5]Ginkel I，Um lauf G.Analyzing a generalized loop subdivision scheme[J].Computing，2007，79（2/4）：353-363.

[6]Am resh A，Farin G，Razdan A.Adaptive subdivision schemes for triangular meshes[M]//Hierarchical and Geometric Methods in Scientific Visualization.Berlin：Springer-Verlag，2003.

[7]Pakdel H R，Samavati F F.Incremental adaptive loop subdivision[C]//Proceedings of ICCSA，2004：237-246.

[8]胡和平.自适应Catmull-Clark细分算法[J].华中科技大学学报，2002，10（10）：56-58.

[9]李桂清，吴壮志，马维银.自适应细分技术研究进展[J].计算机辅助设计与图形学学报，2006，18（12）：1789-1799.

[10]吴剑煌，刘伟军，王天然.面向三角网格的自适应细分[J].计算机工程，2006，32（12）：14-16.

[11]钟大平，周来水，周海.自适应混合细分算法研究[J].机械科学与技术，2004，23（9）：1090-1092.

[12]李李，王亚平.裁剪曲面自适应三角化剖分[J].计算机应用，2006（S1）：2-13.

[13]赵宏庆，彭国华，叶正麟，等.自适应细分方法进行曲面造型[J].计算机应用研究，2006（9）：72-76.

[14]王艳艳，张荣国，王蓉，等.向量线性相关的三角网格自适应Loop细分方法[J].工程图学学报，2009（1）：91-96.

[15]Schroeder W J，Zarge J A，Lorensen W E.Decimation of triangle meshes[J].ACM SIGGRAPH Computer Graphics，1992，26（2）：65-70.

[16]罗鹍，黄魁东，连明明.基于顶点删除的三角网格模型简化新方法[J].微电子学与计算机，2009（5）：142-144.

[17]王焕.点到空间直线距离公式的两种简洁证明[J].高等数学研究，2006，9（2）：38-39.