关联噪声对集合种群稳定性和平均灭绝时间的影响

王国威，程庆华，徐大海

（长江大学物理科学与技术学院，湖北荆州434023）

地球上大多数的物种只能生存在一些零散的像斑块一样的区域中，而小环境中的物种因受环境的影响，非常容易灭绝.为了研究这种奇特的生态环境，Levins在1969年提出“集合种群”的概念，其定义为：由经常局部性灭绝，但又重新定居而再生的种群所组成的种群［1－2］.也就是说，集合种群是由空间上彼此隔离，而在功能上又相互联系的两个或两个以上的亚种群或局部种群组成的种群斑块系统.《牛津生态学词典》给出的概念是：由同种种群组成的一个种群群体，这些种群同时存在但又处于不同空间［3］.基于Levins模型基础上，生态学家在集合种群方面做了大量的研究［4－8］.现在，Levins模型被誉为集合种群之母，集合种群是当今国际数学生态学、理论生态学和保护生态学的一个主要研究前沿，其研究为濒危物种及种群的研究提供了新颖的理论依据，也为景观生态学提供深层次的生态与模型机理［9］.

然而，之前的工作大部分局限于确定性的Levins模型，忽略了外部环境和斑块内部的波动效应（噪声）.另外，随着经济的发展，环境受到人类的破坏越来越严重，生境破坏已经成为物种续存和生物多样性保护最严重的挑战.随着人们对生境破坏的持续关注，存在生境破坏的集合种群已经成为当今理论生态学研究的热点之一［10］.Levins［1－2］、Lande［11］、May［8］等在均匀场假设下研究了集合种群动态对生境破坏的响应，得到了著名的Levins原理.而且，在真实环境中，生境破坏可能是随机发生的，因此，考虑经典的存在生境破坏的集合种群模型更具实际意义.

王参军［12］等在Levins模型的基础上研究了噪声对集合种群的稳定性的影响，得到了系统的稳态概率分布函数和平均灭绝时间；李江城［13］等用简化的延时率函数模型对集合种群的稳定性和平均灭绝时间进行了研究；王康康［14］等在Levins模型的基础上研究了色交叉关联噪声对集合种群稳定性的影响.事实上，真正的白噪声是不存在的，因为它需要无穷大的功率才能产生出来，所以色噪声才更接近真实情况，故研究色噪声对集合种群的影响更具典型性.

本文在Levins原理［5，15－16］的基础上，根据经典的存在生境破坏的集合种群模型，考虑存在生境破坏的集合种群的演化过程中不可预知事件（噪声），例如，由于意外的霜冻会使个体的死亡率增加，同时在寒冷多雨的春季也会使得个体的交配成功率降低，这种环境随机性是由于有一些环境上的原因导致了个体之间相关的出生和死亡事件；另一方面，异质种群是斑块生境中小种群的集合，这些种群在空间上存在隔离，彼此间通过个体扩散而相互联系，则在集合种群内部局部种群之间存在相互作用；局部种群趋于灭绝时，个体数量非常少，具有很大的随机性［12－14］.基于以上原因建立随机存在生境破坏的集合种群模型，通过稳态概率密度函数和平均灭绝时间讨论了噪声对系统的稳定性的影响.

1 模型

Levins模型［1－2］可以表示为

其中，x代表被占领的生境斑块的比例，取值为0≤x≤1.e被定义为局部种群的灭绝率，c是一个与扩散个体侵入空的生境斑块有关的参数（在这里所谓侵入指扩散个体不仅能够迁入一个空的生境斑块并且能够在这个空的生境斑块内建立起新的局部种群的过程）.方程（1）的稳态值x′s和非稳态值x′0分别为

当e／c减小时，侵占斑块的比例在平衡态增长.然而，当e／c＜1.0时，集合种群必定会持续的存在下去（x＞0）.Levins模型虽然比较简单，但是它显示了集合种群的重要贡献：如果集合种群持续存活，局部种群重建率远大于灭绝率.具体的讲，e／c＜1.0显示一个被空白斑块包围的局域种群（当x很小时）在其生存期（1／e）内必须至少建立一个新种群才能使集合种群续存下去.

然而，在实际条件下，由于生境的破坏，并不是所有的生境斑块都适合物种生存，根据Levins原理可知，假设有1－h比例的生境斑块遭到永久性破坏，那么就得到经典的存在生境破坏的集合种群模型［7－8，17］：

这时，方程（3）的稳态值xs和非稳态值x0分别为：

集合种群的演化过程中不可预知事件（噪声）是客观存在的［18］，考虑随机环境因素影响灭绝率e，用高斯色噪声ξ（t）代表环境波动，所以，灭绝率e→e＋ξ（t）.另外一方面，异质种群是斑块生境中小种群的集合.这些种群在空间上存在隔离，彼此间通过个体扩散而相互联系，则在集合种群内部局部种群之间具有相互作用.局部种群趋于灭绝时，个体数量非常少，具有很大的随机性，这里我们认为这种随机性为种群内部的随机性，并且引入高斯白噪声η（t）来表示这种内部随机性.内部噪声和外部噪声是非同源的，但是由于外部环境的涨落可以影响内部因素的涨落，所以内部噪声就不再是独立的，它们之间存在关联.

综合以上因素，根据方程（3）得到集合种群的随机演化方程，即一维无量纲郎之万方程［19－21］：

式中，ξ（t）和η（t）分别为高斯色噪声和白噪声，其统计性质［22－24］为：

其中，D和Q分别表示乘性噪声和加性噪声强度，τ是乘性噪声自关联时间，λ表示两噪声间的关联强度，且－1≤λ≤1.式（5）中关于变量x的确定势函数为：

2 噪声对集合种群稳定性和平均灭绝时间的影响

根据Stratonvich积分得到方程（5）和（6）对应的Fokker－Planck方程［25－26］：

其中，P（x，t）为概率分布函数，A（x）和B（x）分别为：

式中，f（x）＝cx（h－x）－ex.在定态条件下，根据方程（8）～（10）可以得到稳态概率分布函数为：

式中，

对于集合种群，生态学家关心的是什么时候种群趋于灭绝［27－28］，即集合种群从稳定态xs趋于灭绝态x0所需的时间.平均首次通过时间是系统从一个稳态出发穿越势垒进入另一个势阱所用时间的平均值，它是随机动力学理论研究的一个重要问题.对于集合种群理论而言，从物种占有率斑块最大的时间开始，直到物种在斑块灭绝的这段时间被称为物种的灭绝时间Tex；而从物理的角度理解，从相空间内一个初始位置为使Pst（x）为极大值的x0的相粒子逃逸到0的平均时间作为系统的平均首次通过时间T（x0）.那么根据文献［13］的描述，物种的灭绝时间可以由Tex＝T（x0→0）求得，故这里我们用平均首次通过时间衡量灭绝时间［29］.灭绝时间的精确表达式为［29－30］

式中，x0＝0为系统的不稳态，T（xs→x0）表示集合种群从稳定态xs＝h－过渡到灭绝态x0＝0所需的平均时间.由于（16）式的处理难度较大，因而当D和Q很小且远小于势垒ΔU（x）＝U（x0）－U（xs）时采用最快下降法［31］，得到平均首通时间的表达式为［32］

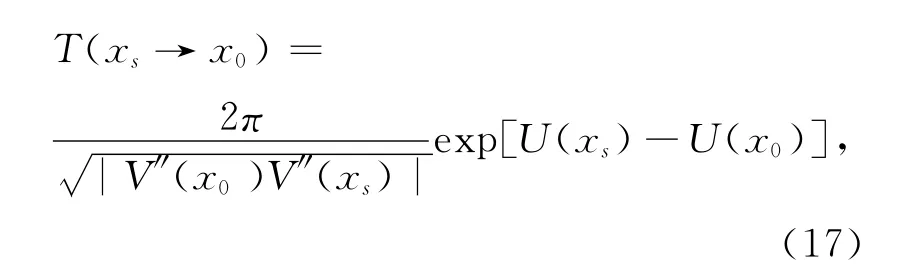
其中，V（x）和U（x）的表达式分别由式（7）和（12）给出.

图1 稳态概率分布函数Pst（x）作为x的函数（以D、Q为参数）Fig.1 The stationary probability density Pst（x）as a function of x or different D and Q

根据方程（11）做出稳态概率分布函数Pst（x）作为x的函数，当其他参数固定，D和Q变化时，如图1（a）和（b）所示.从图1（a）可以看出：随着乘性噪声强度D的增大，Pst（x）峰值的位置逐渐向左移动，且峰值变小，但是当D＞0.5时（在本文所选取的参数条件下），其峰值随D的增加而逐渐变大.由于峰值所在位置表示的是被占据的生境斑块的比例，所以D的增大导致被占据的生境斑块的比例减小.同时，Pst（x）的峰值高度先减小后增大，说明被占据的生境斑块的比例在该处的概率先减小然后增大.所以，图1（a）告诉我们：一定范围内乘性色噪声强度的增加，会弱化集合种群的稳定性.从图1（b）可以看出：随着加性噪声强度Q的增大，峰值所在的位置xs基本不随Q的变化而改变.但是，图1（b）中比较引人注意的是，随着Q的增加，Pst（x）在xs处的峰值迅速减小，并且峰值逐渐消失，最后变成一条关于x的单调函数.因xs代表的是系统的稳态值，故被占据的生境斑块的比例在xs的概率迅速减小.所以Q的增大使得集合种群的稳定性迅速下降并最终促使集合种群灭绝.集合种群从稳定态xs转向灭绝态x0，系统发生相变.综合两图可以看出，乘性色噪声强度D和加性白噪声强度Q增大时均起到弱化集合种群稳定性的作用.

图2 稳态概率分布函数Pst（x）作为x的函数（以τ、λ（λ＜0）为参数）Fig.2 The stationary probability density Pst（x）as a function of x for differentτandλ（λ＜0）

根据稳态概率分布函数Pst（x）的表达式，固定其他参数，改变乘性噪声间自关联时间τ，Pst（x）随x的变化图像如图2（a）所示.从图可以看出：Pst（x）随x的变化过程中呈现一个单峰曲线，且随着τ增加，Pst（x）峰值高度逐渐变大，说明被占据的生境斑块的比例在xs处的概率逐渐增加，这对集合种群的生存是有利的.另外，随着乘性噪声间自关联时间的增加，峰值的位置逐渐向右移，表明集合种群所占领的生境斑块的比例变大，这对集合种群有积极作用.综合上述分析，我们发现，乘性噪声间自关联时间的增加，增强集合种群系统的稳定性.

当其他参数固定时，以噪声间关联强度λ为参数，稳态概率分布函数Pst（x）随x变化的图像如图2（b）和图3所示.其中，图2（b）是两噪声间负关联（λ＜0）时的情形，图3是两噪声间正关联（λ＞0）时的情形.从图2（b）可以看出，两噪声间负关联时，随着｜λ｜的增加，Pst（x）的峰值逐渐左移，即集合种群占据生境斑块的比例变小.同时，峰值的高度变小，说明被占据的生境斑块的比例在xs处的概率减小.故两噪声间负关联时，｜λ｜的增加弱化了集合种群的稳定性，对集合种群的生存繁衍有消极作用.

图3 稳态概率分布函数Pst（x）作为x的函数（以λ（λ＞0）为参数）Fig.3 The stationary probability density Pst（x）as a function of x for differentλ

图4 平均首次通过时间T（xs→x 0）作为D的函数（以λ为参数）Fig.4 The mean first－passage time T（xs→x 0）as a function of x for differentλ

当两噪声间正关联时，稳态概率分布函数Pst（x）随x变化的图像如图3所示，对比图2（b）和图3两图可以看出，图3的图像变化趋势明显不同于图2（b）.其不同之处在于图2（b）中，Pst（x）曲线出现了一个类似于波谷的极小值和一个类似于共振峰的极大值，但是在图3中，Pst（x）只出现了一个类似于共振峰的极大值.同时，图2（b）中Pst（x）峰值的宽度较大而高度较小，然而在图3中Pst（x）则是波峰宽度较小，但是高度较大.另外，我们发现，在正关联的时候，随着｜λ｜的增加，Pst（x）的峰值逐渐右移，即集合种群占据的生境斑块的比例增加；同时，峰值变大说明被占据的生境斑块的比例在xs处的概率增加，这对集合种群的生存和繁衍是有积极意义的，故正关联时关联强度的增加可以增强集合种群系统的稳定性.因此噪声间正、负关联对集合种群稳定性产生不同的作用：λ＜0时，｜λ｜的增加弱化了集合种群的稳定性；λ＞0时，｜λ｜的增加增强集合种群系统的稳定性.

图4给出了不同噪声间关联强度下，平均首次通过时间T（xs→x0）与乘性噪声强度D的函数关系.从图4可以看出，当两噪声间负关联时，T（xs→x0）是关于D的单调减函数，即随着乘性噪声强度D的增加，集合种群趋于灭绝的时间变短，故外界环境的波动加剧会加速集合种群趋于灭绝，这和图1（a）的描述是一致的.当两噪声间正关联时，T（xs→x0）是关于D的非单调函数，随着D的增大，T（xs→x0）出现类似共振峰的极大值，表现出“随机共振”的现象；而且，关联强度λ越大，“共振”现象越明显，峰值高度越大，峰值位置逐渐右移.由于“共振”峰的存在，增强了集合种群系统稳定性，抑制了系统相变，延长了种群趋于灭绝的时间，增强了集合种群对外界环境波动的适应性，这对集合种群的生存繁衍是有利的，并且这一点也符合图3当中的描述.

图5作为对图4的一个补充，从图5可以看出，T（xs→x0）是D的非单调函数，随着D的增大，T（xs→x0）出现了类似于共振峰的极大值，表现出“共振”的现象，且乘性噪声间自关联时间τ越大，“共振”现象越明显.由于共振峰的存在，系统稳定性增强，抑制了系统相变，延长了种群趋向灭绝的时间，对种群存生繁衍具有积极意义.故τ的增加延缓了种群的灭绝，集合种群趋于灭绝的时间增加，对延缓种群灭绝起到了积极作用，这符合图2（a）中的描述.图6给出了平均首通时间T（xs→x0）与乘性噪声自关联时间τ之间的函数关系.从图6可以看出：T（xs→x0）是关于τ的单调增函数，即集合种群趋于灭绝的时间随τ的增加而增加，表明集合种群从稳定态到灭绝态需要的时间变长，也就是说集合种群稳定性增强.另外，随着D的增大，T（xs→x0）减小，说明乘性噪声强度的增加促使种群趋于灭绝的时间减小，加速了集合种群的灭绝，表明外界环境的波动弱化了集合种群系统的稳定性，对种群产生不利影响.

图5 平均首通时间T（xs→x 0）作为作为D的函数（以τ为参数）Fig.5 The mean first－passage time T（xs→x 0）as a function of D for differentτ

图6 平均首通时间T（xs→x 0）作为τ的函数（以D为参数）Fig.6 The mean first－passage time T（xs→x 0）as a function ofτfor different D

3 结论

本文在经典的存在生境破坏的Levins模型基础之上，研究了噪声对存在生境破坏的集合种群稳定性的影响，应用Fokker－Planck方程得到了系统的稳态概率概率分布函数和平均首次通过时间，并利用平均首通时间来衡量种群的平均灭绝时间.对计算结果的数值分析表明：

1）加性白噪声的增加弱化了集合种群系统的稳定性，即内部噪声的增加对集合种群产生消极影响，Q的增大使得集合种群的稳定性迅速下降并最终促使集合种群灭绝，集合种群从稳定态xs转向灭绝态x0，系统发生相变；

2）乘性色噪声强度D起到弱化集合种群稳定性的作用，即外界环境的波动对种群产生不利影响；

3）乘性色噪声自关联时间τ的增加增强了集合种群系统的稳定性，即τ可以使集合种群占据生境斑块的比例增加，并促使x0位置处占据生境斑块的比例的概率增加，对集合种群生存繁衍起到有利作用；

4）当两噪声之间的互关联为负关联（λ＜0）时，T（xs→x0）是关于D的单调减函数，即｜λ｜的增加弱化了集合种群的稳定性；当噪声间正关联（λ＞0）时，T（xs→x0）是关于D的非单调函数，随着D的增大，T（xs→x0）出现类似共振峰的极大值，表现出“随机共振”的现象，即｜λ｜的增加增强集合种群系统的稳定性；

5）T（xs→x0）是关于τ的单调增函数.

［1］ Levins R.Some demographic and genetic consequences of environmental heterogeneity for biological control［J］.Bulletin of the Entomological Society of America，1969，15（3）：237－240.

［2］ Levins R.Extinction［J］.Lect Notes Math，1970（2）：75－107.

［3］ Allaby M.Oxford Dictionary of Ecology［M］.Oxford：Oxford University Press，1998.

［4］ Lande R.Risks of population extinction from demographic and environmental stochasticity and random catastrophes［J］.The American Naturalist，1993，142（6）：911－927.

［5］ HanskiI，Moilanen A，Gyllenberg M.Minimum viable metapopulation size［J］.The American Naturalist，1996，147（4）：527－541.

［6］ Amarasekare P.Allee effect in metapopulation dynamics［J］.The American Naturalist，1998，152（2）：298－302.

［7］ Hanski I.Coexistence of competitors in patchy environment［J］.Ecology，1983，64（3）：493－500.

［8］ Nee S，May R M.Dynamics of metapopulation：habitat destruction and competitive coexistence［J］.J Anim Ecol，1992，61（1）：37－40.

［9］ Tilman D，Kareiva P.Spatial Ecology：The Role of Space in Population Dynamics and Interspecific Interactions［M］.Princeton：Princeton University Press，1997.

［10］ Otso O.Habitat destruction，restoration and eigenvectr－ei－genvalue relations［J］.Mathematical Biosciences，2003，181：165－176.

［11］ Lande R.Extinction thresholds in demographic models of territorial population［J］.American Naturalist，1987，130（4）：624－635.

［12］ 王参军，李江城，梅冬成.噪声对集合种群稳定性的影响［J］.物理学报，2012，61（12）：120506.

［13］ 李江城，梅冬成.集合种群的延时效应［J］.物理学报，2008，57（11）：6792－6798.

［14］ 王康康，刘先斌，杨建华.色交叉关联噪声作用下集合种群的稳定性和平均灭绝时间［J］.物理学报，2013，62（10）：100502.

［15］ Jordi B，Ricard V S.Effects of habitat destruction in a prey－predator metapopulation model［J］.J Theor Bio，1998，195（3）：383－393.

［16］ Hanski I.Metapopulation Ecology［M］.Oxford：Oxford U－niversity Press，1999.

［17］ Moilanen A，Hanski I.Metapopulation dynamics：effects of habitat quality and landscape structure［J］.Ecology，1995，79（7）：2503－2515.

［18］ May R M.Simple mathematical models with very complicated dynamics［J］.Nature，1976，261（5560）：459－467.

［19］ Nie L R，Mei D C.Effects of time delay on symmetric twospecies competition subject to noise［J］.Phys Rev E，2008，77（3）：031107－031112.

［20］ Li J H，Huang Z Q.Transport of particles caused by correlation between additive and multiplicative noise［J］.Phys Rev E，1998，57（4）：3917－3922.

［21］ Nie L R，Mei D C.Fluctuation－enhanced stability of a metapopulation［J］.Phys Lett A，2007，371（1）：111－117.

［22］ 程庆华，曹 力，吴大进，等.关联噪声驱动下单模激光系统的随机共振现象［J］.华中科技大学学报：自然科学版，2004，32（3）：32－33.

［23］ 陈 俊，成传明.Logistic模型中的负关联噪声效应［J］.华中师范大学学报：自然科学版，2008，42（2）：207－210.

［24］ Chen J，Xie H，Chen P.Bistable kinetic model driven by correlation O－U noises［J］.Journal of Huazhong Normal U－niversity Nat Sci，2003，37（1）：38－41，50.

［25］ Mei D C，Xie G Z，Cao L，et al.Transient properties of a bistable system driven by cross－correlated noises：correlation times are nonzero case［J］.Chin Phys Lett，1999，16（5）：327－329.

［26］ Xie C W，Mei D C.Mean first－passage time of a bistable kinetic model driven by multiplicative colored noise and additive white noise［J］.Chin Phys Lett，2003，20（6）：813－816.

［27］ Bak P，Sneppen K.Punctuated equilibrium and criticality in a simple model of evolution［J］.Phys Rev Lett，1993，71（24）：4083－4086.

［28］ Ovaskainen O，Hanski I.From individual behavior to metapopulation dynamics：unifying the patchy population and classic metapopulation models［J］.The American Naturalist，2004，164（3）：364－377.

［29］ Lindenberg K，West B J.The first，the biggest，and other such considerations［J］.Journal of Statistical Physics，1986，42（1－2）：201－243.

［30］ Masoliver J，West B J，Lindenberg K.Bistability driven by Gaussian colored noise：First－passage times［J］.Phys Rev A，1987，35（7）：3086－3094.

［31］ 胡 岗.随机力与非线性系统［M］.上海：上海科技教育出版社，1994.

［32］ 赵 燕，徐 伟，邹少存.非高斯噪声激励下FHN神经元系统的定态概率密度与平均首次穿越时间［J］.物理学报，2009，58（3）：1396－1402.