基于速率变化的最优参数化

陈 军， 周 联

(1.宁波工程学院理学院, 浙江 宁波 315211；2.上海海事大学文理学院, 上海 201306)

Chen Jun1, Zhou Lian2

(1.Faculty of Science, Ningbo University of Technology, Ningbo Zhejiang 315211, China;2.Liberal Arts & Sciences College, Shanghai Maritime University, Shanghai 201306, China)

参数曲线在CAD/CAM的各项应用中，往往需要取其参数为弧长参数。这是由于弧长参数能够使得在参数域内均匀分布的点对应曲线上均匀分布的点，即参数的速率保持匀速不变。这种直观的几何意义和良好的几何性质，使其在模具加工的实时插补算法、曲线求交以及几何外形分析等研究中占有重要的地位。

但是，文献[1]指出除了直线以外，多项式/有理形式的参数曲线其参数不可能为弧长参数。为此，文献[2]利用Möbius变换，通过对曲线速率和单位速率之间的L2范数进行最小化操作，得到了Bézier曲线的“最优参数化”。 这种方法不仅有严谨的数学理论支持，而且能够事先直接提供用于优化的显式表达式而无需实时计算，可以较好地应用于实际。在此基础上，一系列改进和推广最优参数化的工作不断出现：文献[3]极大地简化了最优参数化的中间步骤，得到了与文献[2]相同的结果；文献[4]在进行Möbius变换前事先对参数域进行分段，取得良好的效果；文献[5]给出了一种不同于Möbius变换的的分式变化，使得计算过程更简单；文献[6]利用遗传算法，使参数速率偏离单位速率的最大值达到最小；文献[7-8]利用积分公式得到了用于最优参数化有理二次Bézier曲线的精确解析解；文献[9]分别从代数和几何两个角度得到了一次复有理Bézier曲线的最优参数化；文献[10]则把最优参数化从参数曲线推广到了平面二次曲线。

1 最优参数化

设P(t)(t∈[0,1])是一条n阶Bézier曲线，对其参数t进行Möbius变换：

能使P(tα(u))的表达式为一条有理Bézier曲线，其控制顶点与P(t)相同，而权因子为显然，Möbius变换并不改变曲线P(t)的外形，仅仅改变其参数分布而已。

文献[2]利用定积分：来衡量当前参数与弧长参数的差距，J越小则表示其越接近于弧长参数。那么，最优参数化即为寻找一个α∈(0,1)，使得达到最小。

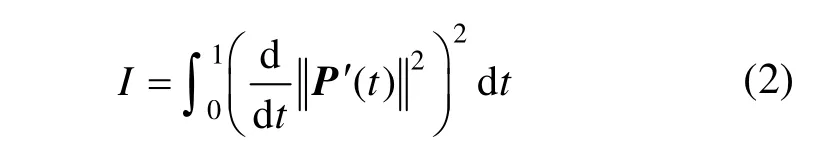
与以往的研究不同，本文用下述定积分：来取代式(1)。对比式(1)与式(2)：式(1)描述的是曲线的速率大小，而式(2)描述的是曲线速率变化率的大小，因此将式(2)中的定积分I称为速率变化量。当曲线取弧长参数时，其参数速率为恒值，此时速率变化量I能够取到最小值I=0。因此，速率变化量I也能够合理地衡量当前参数的优劣：I越小，则参数速率越接近于均匀速率。

为此，需要寻找一个变换，使得变换后的曲线表达式其速率变化量I达到最小。但是，如果仍沿用Möbius变换，速率变化量I的计算将十分复杂。受文献[4]的启发，对参数域进行分段，用分段线性变换来代替Möbius变换，从而把分段节点作为自由度，使得经过分段线性变换后的曲线表达式其速率变化量I达到最小。此时，与以往的最优参数化不同，新生成的曲线表达式不再是有理Bézier曲线，而是一系列多项式Bézier曲线。

2 问题的描述

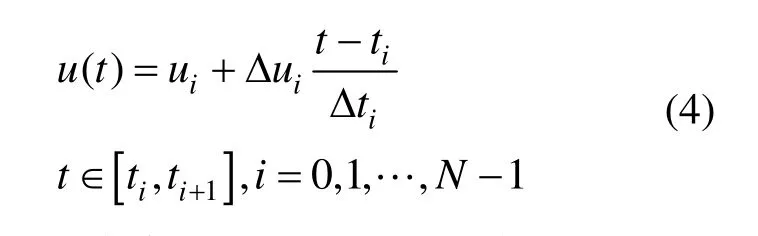
那么，基于速率变化量I的最优参数化问题为：给定一条n阶Bézier曲线P(t)以及一组满足0=t0＜t1＜…＜tN-1＜tN=1的点列，求满足0=u＜u＜…＜u＜u=1的点列，使得

01N-1N P(t)经过如式(3)的分段线性变换t(u)后，下述定积分达到最小：

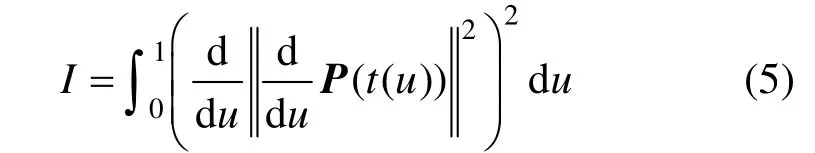
根据式(3)～(4)，可得：

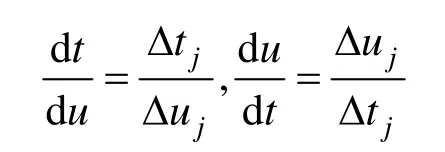
那么，对式(5)作进一步化简，有：

这里，

若要使得I取到最小，需要满足：

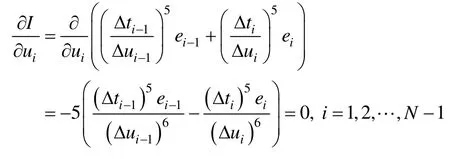
上述N-1个方程虽然不是线性方程，但是经过计算，Δui可以由Δu0简单表达：

4 数值实例

图1～3对3条曲线进行了基于速率变化的最优参数化。为方便起见，其用于分段的节点取均匀节点图中还给出了由文献[2]得到的参数速率。通过观察可得，两者在不同的区域其速率各有优劣，但本文的方法使得曲线较少出现部分区域速率过大的情况。表1给出了在节点数N取不同的值时，相应的速率变化量IN的值。我们发现，文献[2]的最优参数化在本文的标准下并不总能改善曲线的速率。显然，随着节点数N的增大，用于最优参数化的自由度将增加，相应的速率变化量IN的值将减小。根据经验，一般取N=7即可得到满意的效果。需要注意的是，虽然在最优参数化后，曲线的速率不连续，但是曲线本身形状并不发生改变。

图1 曲线1及其重新参数化后的曲线速率

图2 曲线2及其重新参数化后的曲线速率

图3 曲线3及其重新参数化后的曲线速率

表1 节点数增加时速率变化量IN(N=3,5,7)的变化趋势

5 结 论

本文用分段线性变换代替Möbius变换，把分段节点作为自由度，对曲线进行最优参数化。同时，对参数优劣的衡量标准进行了改进，使最优参数化后的曲线速率其变化率达到最小。特别地，本文采用的分段线性变换使得最优参数化后的曲线仍为Bézier曲线，这有助于对于曲线的进一步分析。最后给出的数值实例验证了算法的有效性。近年来，陆续有一些研究成果把最优参数化从曲线拓展到曲面上[11-13]，取得了良好的效果。如何把本文的衡量标准相应地推广到Bézier曲面上，将是我们进一步研究的内容。

[1]Farouki R T, Sakkalis T.Real rational curves are not‘unit speed’ [J].Computer Aided Geometric Design,1991, 8(2): 151-157.

[2]Farouki R T.Optimal parameterizations [J].Computer Aided Geometric Design, 1997, 14(2): 153-168.

[3]Jüttler B.A vegetarian approach to optimal parameterizations [J].Computer Aided Geometric Design, 1997, 14(9): 887-890.

[4]Costantini P, Farouki R T, Manni C, Sestini, A.Computation of optimal composite re-parameterizations [J].Computer Aided Geometric Design, 2001, 18(9): 875-897.

[5]郭凤华, 杨兴强.C-Bézier曲线的一种重新参数化新方法[J].工程图学学报, 2006, 27(2): 108-111.

[6]郭凤华.参数曲线的最优参数化[J].计算机辅助设计与图形学学报, 2007, 19(4): 464-467.

[7]陈 军, 王国瑾.2 次有理Bézier曲线的最优参数化[J].计算机研究与发展, 2008, 45(9): 1601-1604.

[8]Cattiaux-Huillard I, Albrecht G, Hernández-Mederos V.Optimal parameterization of rational quadratic curves [J].Computer Aided Geometric Design, 2009,26(7): 725-732.

[9]黄伟贤, 王国瑾.一次复有理Bézier曲线的最优参数化[J].计算机辅助设计与图形学学报, 2010, 22(11):1972-1977.

[10]厉玉蓉, 胡芳刚.平面二次代数曲线的最优参数化[J].图学学报, 2012, 33(2): 49-52.

[11]Yang Yijun, Yong Junhai, Zhang Hui, Paul J C, Sun Jiaguang.Optimal parameterizations of Bézier surfaces [C]//Bebis G, et al.ISCV 2006, LNCS 4291.Berlin Heidelberg: Springer-Verlag, 2006: 672-681.

[12]Li Yufei, Wang Wenping, Tu Changhe.Optimal sampling of parametric surfaces [J].Computer-Aided Design & Applications, 2012, 9(1): 55-60.

[13]Yang Yijun, Zeng Wei, Yang Chenglei, Deng Bailin,Meng Xiangxu.Sitharama Iyengarc.An algorithm to improve parameterizations of rational Bézier surfaces using rational bilinear reparameterization [J].Computer-Aided Design, 2013, 45(3): 628-638.