一种改进的Roberts和灰色关联分析的边缘检测算法

文永革， 何红洲， 李海洋

(绵阳师范学院数学与计算机科学学院，四川 绵阳 621000)

边缘检测一直是图像处理中的研究热点，在模式识别、机器视觉等领域具有广泛应用。常用的边缘检测方法是利用检测模板或算子，如Sobel、Prewitt、Robert、Laplacian等[1-2]进行计算。王智文[3]对Sobel、Prewitt、Robert、Laplacian、Canny、Gaussian和Zero-Cross等算子算法的性能进行了比较研究，用实验证明了不存在占绝对优势的检测算法。姜庆玲[4]将细胞神经网络(cellular neural network,CNN)数学模型应用到图像边缘检测中，可直接检测彩色图像边缘。朱晓临等[5]提出一种多阈值选取与改进的边缘连接相结合的方法，使边缘检测能保持弱边缘和连接性。针对一些特殊应用，文献[6-8]分别把遗传算法、复合导数、数学形态学等理论运用到图像边缘检测中，并取得了较好效果。针对Roberts算法对噪声比较敏感且需要人为指定阈值问题，康牧等[9]提出了一种Roberts自适应边缘检测方法，能够自适应地生成动态阈值，提高了图像边缘细节信息的提取性能。

灰色系统理论是邓聚龙[10]提出的一种研究少数据、贫信息、不确定性或不完全确定系统问题的新方法，主要解决一些包含未知因素的特殊领域问题，并得到了广泛应用。文献[11-13]将灰色关联度与图像的边缘检测相结合，提出了一种利用Sobel算子作为参考序列，通过计算灰色关联度来检测图像边缘的算法(简称为Sobel灰关联算法)，并获得了初步成果。

但以上算法在权衡边缘检测精度、定位精度和抗噪性的问题上还存在不足。

本文结合灰色关联分析方法，提出一种改进的Roberts边缘检测算法。首先对Roberts算子进行了改进，以提高其检测精度和抗噪性。然后将改进后的Roberts算子和灰色关联分析相结合，以改进后的Roberts算子作为参考序列，通过计算灰色关联度来检测图像边缘，从而有效地提高了边缘检测效果。

1 Roberts算子及其改进

1.1 Roberts算子

Roberts算子是一种简单高效的算子，它采用对角线方向相邻像素之差近似梯度幅值检测边缘，在处理图像像素时，可看成梯度幅值的近似计算方法。故其梯度幅值运用差分方法[14-15]计算如下：

fx卷积算子为：

fy卷积算子为：

其梯度幅值为：

Roberts边缘检测算子采用对角线方向相邻像素之差进行梯度检测。算法只考虑对角线方向4个像素信息，忽略了水平相邻像素和垂直相邻像素信息。如果水平相邻像素或垂直相邻像素是灰度值变化缓慢的局部边缘，算法则无法检测到。并且，由于像素点本身直接参与运算，导致算法不能有效抑制噪声干扰。

1.2 Roberts改进算子

针对Roberts算子的不足，充分考虑像素8个邻域的信息。在梯度幅值计算时，在原Roberts算子基础上，增加了水平和垂直方向信息，如图1所示。

图1 Roberts算子梯度幅值计算改进

其梯度幅值计算方法如下：

水平差分:fx=f(i,j+1)-f(i,j-1)

垂直差分：fy=f(i-1,j)-f(i+1,j)

45°差分：f45=f(i-1,j+1)-f(i+1,j-1)

135°差分：f135=f(i-1,j-1)-f(i+1,j+1)

它们对应的卷积算子为：

Roberts边缘检测算子采用对角线方向相邻两像素之差进行梯度幅值检测，检测定位精度比较高。但由于像素点本身直接参与运算，导致算法对噪声敏感。改进算子充分考虑了像素点8个邻域信息，避免了像素点本身直接参与运算，这样不仅可以保持原Roberts算子定位精度高的优点，而且可以有效抑制噪声，获得更优的检测效果。

改进后Roberts算子4方向差分幅值计算式为：

2 灰关联分析法

根据灰色系统理论[10]，灰关联分析法是通过对系统特征行为序列和系统因素行为序列曲线间几何形状的分析比较，在因素序列中找出和特征序列曲线形状变化最近似的序列，即可认为两条曲线几何形状相似，则关联度较大。其灰色关联度计算方法如下：

设X0={x0(t),t=1,2,…,n}为参考序列，Xi={xi(t),t=1,2,…,n;i=1,2,…,m}为被比较的行为序列，那么Xi和X0在t时刻的关联系数为：

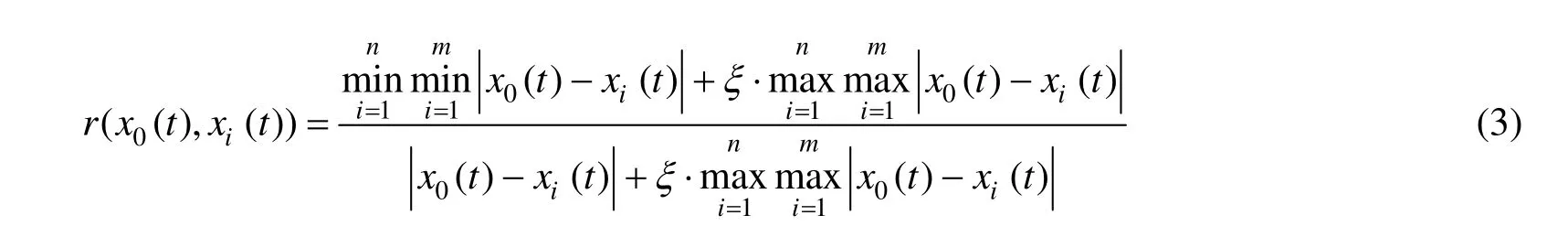
ξ为分辨系数，一般取ξ=0.5。则参考序列X0与行为序列Xi之间的灰色关联度R(x0,xi)为：

3 Roberts算子与灰色关联分析结合

基于数理统计的分析方法往往需要大量数据样本且服从典型分布，而数字图像的数据，其分布往往是随机的而不服从典型分布。所以用数理统计分析方法来检测图像边缘不太恰当。灰色关联分析法可把一切随机过程看做是一定范围内变化的灰色过程，对数据分布类型和样本量无特殊要求。因此，根据数字图像的数据分布特性，可以将一幅图像作为一个灰色系统进行优化处理[17]。处理方法如下：把图像的每个像素点及其8个邻域作为行为序列，以Roberts改进算子作为参考序列，计算出两个序列的灰色关联度，然后根据阈值作判定：如果关联度大，则判定该像素点为边缘点；如果关联度小，则不是边缘点。具体步骤如下：

3.1 行为序列的确定

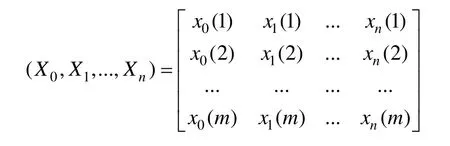
设一幅m×n像素的图像，其评价数据可以分为n个数据序列：其中，像素点X(i,j)及其8邻域空间位置关系如图2所示。

则各像素点及其邻域灰度构成的行为序列为：

其中，i=1,2,···,m；j=1,2,···,n。在图像外边框部分像素邻域数目少于8个，可作补零操作，本文在此不作详细讨论。

图2 像素点Xi,j及其邻域

3.2 参考序列的确定

以改进后的Roberts卷积算子为模板对空间域滤波就可以得到图像边缘，所以Roberts改进算子反映了图像边缘像素的分布特性。因此，在计算图像中各点的关联度时，可以使用Roberts改进算子作为参考序列。根据1.2节中改进的卷积算子，形成参考序列如下：

3.3 目标数据序列的无量纲化

如果目标数据序列的单位不同，会对关联分析产生影响，因此需要对目标数据序列进行无量纲化处理。

设Xi=(xi(1),xi(2),…,xi(n))为一个行为序列，

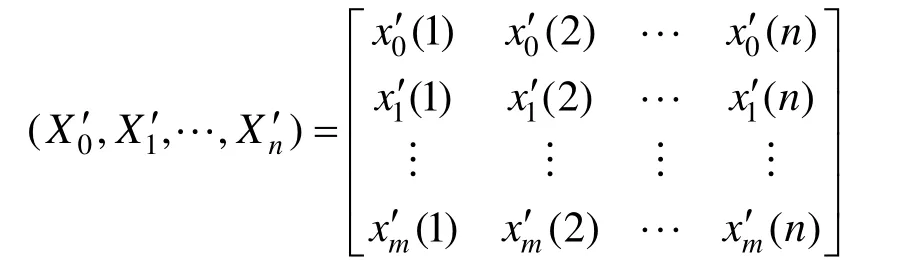
对目标数据序列的无量纲方法可采用均值化像法：

其中，i=1,2,···,n ；k=1,2,···,m。

经过目标数据序列的无量纲化处理，在灰色关联度计算中式(3)和式(4)，就可以使用参考序列X0与行为序列Xi的初值像x0′和xi′进行计算。

3.4 求差序列

根据差序列计算公式：

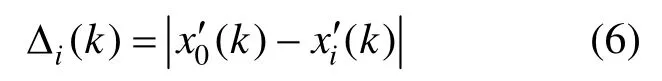
得差值矩阵：

其中，Δi(k)是参考序列和行为序列对应元素的绝对差值，其中，i=1,2,···,n ;k=1,2,···,m。

3.5 最大绝对差值和最小绝对差值的确定

最大绝对差值为：

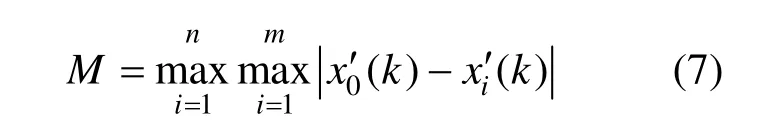
最小绝对差值为：

3.6 关联系数的确定

每个行为序列与参考序列对应元素的关联系数为：

其中，k=1,2,···,m。ξ为分辨系数，它的取值决定灰色关联系数的分布状况。对Sobel灰度关联算法，分辨系数值取0.5。根据文献[18]的分析，分辨系数取值与分辨率成反比，分辨系数小，则分辨率大，反之，分辨率小。若分辨系数取0.05，则适用于分辨率更大的范围，更方便查看关联度变化，比分辨系数取0.5更合理。因此，本研究取分辨系数ξ=0.05。

3.7 灰色关联度的确定

参考序列X0与行为序列Xi之间的灰色关联度

由前可知改进的Roberts算子形成的参考序列有4个，因此，对于任何一点Xi,j及其8邻域形成的四个灰色关联度分别为：设：

Wij代表像素点Xi,j及其8邻域的最大灰色关联度，计算出Wij后，像素点Xi,j是否为边缘的判定依据如下：选取阈值τ，若Wij＞τ时，表示像素点Xi,j在其邻域方向存在边缘特性，则像素点Xi,j为边缘点；否则，像素点Xi,j就不是边缘点。

4 实验结果与分析

本研究在Intel Core2 P8600 @ 2.40 GHz，4 GB内存的环境下，采用Matlab7.0和Microsoft Visual Studio 2005在多幅图像上交叉验证了Roberts算子算法、Sobel灰关联算法和GRA-Roberts算法。下面以其中两幅实验图像为例给出实验结果。实验图像1为lenna(图像大小为756 KB；尺寸500×500像素)；实验图像2为dog(图像大小为150 KB；尺寸237×195像素)。

4.1 实验1

在无噪声情况下，对两幅图像使用Roberts算子算法、Sobel灰关联算法和GRA-Roberts算法进行检测，检测结果如图3和图4所示。

从图3和图4可以看出，Roberts算子算法相对于Sobel灰关联算法和GRA-Roberts算法，漏检情况较严重。GRA-Roberts算法较Sobel灰关联算法检测效果表现更好。

4.2 实验2

为验证算法抗噪性能，给dog图像加入高斯噪声和椒盐噪声，分别对Roberts算子算法，Sobel灰关联算法和GRA-Roberts算法进行了抗噪实验。其中，高斯噪声均值为零，标准差为25，实验结果如图5所示。椒盐噪声的椒、盐含量均为0.03，实验结果如图6所示。

图3 lenna图像实验结果

从图5、图6中可以看出，Roberts算子算法相对于Sobel灰关联算法和GRA-Roberts算法，抗噪性较差，GRA-Roberts算法较Sobel灰关联算法抗噪性表现更好。

4.3 比较与分析

在对两幅图像进行边缘检测和抗噪实验同时，对Roberts算子算法、Sobel灰关联算法和GRA-Roberts算法算法运行时间进行了比较。比较结果如表1所示。

图5 含高斯噪声dog图像实验结果

图6 含椒盐噪声dog图像实验结果

表1 不同算法的运行时间比较(ms)

从表1可以看出，在不同情况下，Roberts算子算法运行时间均远低于Sobel灰关联算法和GRA-Roberts算法，说明Roberts算子具有简单、快速，定位精度高的优点。相对于Sobel灰关联算法，GRA-Roberts算法平均运行时间减少约5%，从一定程度上降低了算法时间复杂度。

Roberts算子算法漏检在于算法只考虑对角线方向4个像素信息，忽略了水平相邻像素和垂直相邻像素信息。如果水平相邻像素或垂直相邻像素是灰度值变化缓慢的局部边缘，因算法无法检测而导致目标物体的轮廓边缘的漏检。Roberts算子算法中，待测像素点直接参与了差分幅值的计算，如果像素点具有噪声干扰，会导致幅值计算结果偏大，所以Roberts算子抗噪性差。GRA-Roberts算法边缘检测效果和抗噪性表现相对较好，原因在于GRA-Roberts算法对Roberts算子进行了改进。对待检像素点，GRA-Roberts算法通过求其8邻域的四方向差分幅值来计算的，并较为充分地考虑了其水平和垂直方向的邻域信息及其对角线邻域的权值，所以检测效果较好。并且，GRA-Roberts中待检像素点本身不直接参与运算，可以使噪声得到有效抑制，故对噪声敏感度降低。此外，GRA-Roberts算法在计算灰色关联度时充分考虑了参考序列与行为序列的分辨率，使灰色关联度取值更加合理，所以具有更好的检测效果。

5 结 论

针对Roberts算子在图像边缘检测中存在的不足，采用优化后的Roberts算子，结合灰色关联分析，提出了一种基于灰色关联分析的图像边缘检测方法Roberts算子算法。该算法既保留了Roberts算子简单、定位精度高的优点，又对Roberts算子易产生漏检、抗噪性低的缺点进行了改进。实验结果表明，GRA-Roberts算法比Roberts算子算法具有更好的检测精度和抗噪性，比Sobel灰关联算法降低了时间复杂度。

[1]Singh H,Kaur T.Empirical study of various edge detection techniques for gray scale images [J].International Journal of Advanced Research in Computer Science and Software Engineering,2013,3(8): 76-80.

[2]Bansal B,Saini J S,Bansal V,Bansal B,Saini J S,Bansal V,Kaur G.Comparison of various edge detection techniques [J].Journal of Information and Operations Management,2012,3(1): 103-106.

[3]王智文.几种边缘检测算子的性能比较研究[J].制造业自动化,2012,34(6): 14-16.

[4]姜庆玲.基于细胞神经网络鲁棒性的彩色图像边缘检测[J].图学学报,2013,34(1): 22-30.

[5]朱晓临,邓祥龙,胡德敏.多阈值选取与边缘连接的边缘检测算法[J].图学学报,2012,33(2): 72-76.

[6]王金凤,焦斌亮.基于数学形态学的彩色图像边缘检测[J].工程图学学报,2011,32(6): 43-46.

[7]程金梅,叶永强,姜 斌.利用复合导数的边缘检测新算法[J].中国图象图形学报,2012,17(3): 393-401.

[8]李 杰,彭月英,元昌安,林 墨,王仁民.基于数学形态学细化算法的图像边缘细化[J].计算机应用,2012,32(2): 514-516,520.

[9]康 牧,许庆功,王宝树.一种Roberts自适应边缘检测方法[J].西安交通大学学报,2008,42(10): 1240-1244.

[10]邓聚龙.灰色系统基本方法[M].武汉: 华中科技大学出版社,2005: 76-105.

[11]王康泰,戴文战.一种基于Sobel算子和灰色关联度的图像边缘检测方法[J].计算机应用,2006,26(5):1035-1036,1047.

[12]兰 丽,胡晓辉,孙苗强.一种基于灰关联和Sobel算子的完全非结构化道路边缘检测方法[J].湖南工程学院学报(自然科学版),2013,23(1): 42-44.

[13]周 龙,陈绵云.基于灰关联分析的储粮害虫图像边缘检测算法[J].华中科技大学学报(自然科学版),2005,33(4): 61-63.

[14]孙士保,段建辉.一种基于边缘梯度的图像插值算法[J].计算机工程,2013,39(8): 239-242.

[15]Zhang Junying.Edge detection in glass fragmentation images based on one order differential operator [C]//2010 Second International Conference on Computer Engineering and Applications.Bali Island,Indonesia,2010,2: 591-594.

[16]李弼程,彭天强,彭 波.智能图像处理技术[M].北京: 电子工业出版社,2004: 149-172.

[17]钟都都,闫 杰.基于灰色关联分析和Canny算子的图像边缘提取算法[J].计算机工程与应用,2006,42(28): 68-71.

[18]申卯兴,薛西锋,张小水.灰色关联分析中分辨系数的选取[J].空军工程大学学报(自然科学版),2003,4(1): 68-70.