基于二项式系数设计矩阵的Bézier曲线扩展

郭大勇， 成佳颐

(清华大学机械工程系，北京 100084)

在计算机辅助几何设计(computer aided geometric design,CAGD)和计算机图形学(computer graphics,CG)领域中，常利用参数化的曲线曲面来进行交互式设计。当在表示曲线或曲面的时候，如果想要保持曲线曲面的形状，很重要的一点就是基函数的选取。因此，以Bernstein多项式作为基函数的Bézier曲线曲面模型有着广泛的应用[1]。但是该模型的不足之处在于，若需要根据需求调整Bézier曲线曲面的形状，就必须对原始控制点进行调整，这不便于实际使用。为了改善这种情况，一种可行的方法就是对Bernstein基函数添加形状参数，使得在原始控制点不变的情况下，实现对Bézier曲线曲面的调整。

近些年来，这种Bézier曲线的扩展方法大致分成三类[2]，分别为利用三角多项式思想;利用代数双曲思想和利用多项式思想。其中，利用多项式思想的Bézier曲线扩展的研究成果如下：文献[3-6]分别给出了Bézier曲线的二次，三次，四次和五次含参扩展。文献[7-10]给出了Bézier曲线的n次含参扩展，其中文献[7-9]直接给对应的基函数表达式，而在文献[10]中，作者利用de Casteljau算法将4次含参Bernstein基函数递推到了n次。

本文根据二项式((1-t)+t)n-1的展开系数，引入含参的正系数矩阵Ann，在此基础上推导出了同阶含参的A-Bernstein基函数表达式，该表达式与Bernstein基函数具有类似的性质，对应A-Bézier曲线不仅有Bézier曲线的特性，而且可以通过改变参数来实现对曲线的调整。另外，通过对正系数矩阵Ann进行调节，亦可以实现对A-Bézier曲线的调整，使曲线的调控更加灵活。

1 正系数矩阵的推导及几何解释

定义1.当aij≥0(i,j=1,2,…,n)时

为所需的正系数方阵。

定义2.当t∈[0,1]，i=1,2,…,n时，称关于t的多项式：

为n–1次Bernstein基函数，恰好对应二项式1((1-t)+t)n-1的展开项。其作为n–1次Bézier曲线的基函数，具有诸多优良性质，如正性、权性和对称性等。

定义3.对于[]0,1t∈，Bézier曲线的控制多边形顶点为p1,p2,…pn，则对应的Bézier曲线方程的矩阵形式为：

利用正系数矩阵Ann对Bernstein基函数矩阵进行调配，可得A-Bernstein基函数Tnn=AB。为了使满足权性=1和对称性可令Ann具有以下性质：

性质1.

性质2.

因此，A-Bernstein基函数对应的A-Bézier曲线为

对应的控制点矩阵：

其中，=p1a1m+p2a2m+…+pnanm,m=1,2,…,n

新的控制点为原始控制点的加权平均，为了减少计算量，限定新的控制点为两点加权平均，并分情况给出表达式：

(1) 当2,2,3,n=mm=…时

其中i=2,3,…,m，j=m+1,m+2,…,n-1

(2) 21,2,3,nmm=+=…时

其中i=2,3,…,m，j=m+2,m+3,…,n-1

若已知，根据性质2，可得pj。且根据性质1可知=ai-1,ipi-1+ai,ipi，其代表的几何意义为：点按比例分线段如图1所示。

图1 线段的定比分点

向式(1)中引入参数λ，通过改变λ的值来实现对新控制多边形的调整，从而实现对A-Bézier曲线的调整。由于式(2) 依次对应了二项式((1-t)+t)n-1的展开项，为了减少计算量和简化表达式，令式(1)中元素的分母与((1-t)+t)n-1的展开项系数相同，可得aij的分母为且规定当时，aij=1。对于式(1)的同一列上的两个元素aij的分子，本文做如下分析：

为了保证扩展后的含参数λ的A-Bernstein基函数(t)在t∈[0,1]上随着t的变化保持单调递减，并且在0处取得最大值1，在1处取得最小值0。限定(t)=(1-λt)(1-t)n-2，因此可得式(1)的第一行：

根据性质2可得Ann的最后一行：

对于正系数矩阵(1)的同一列上的两个元素aij的分子，取其中一个为(1-)λ，另一个可根据性质1求得，因此可得：

(1) 当n=2m,m=2,3,…时

其中i=2,3,…,m，j=m+1,m+2,…,n-1

(2) 当n=2m+1,m=2,3,…时

其中，i=2,3,…,m，j=m+2,m+3,…,n-1且当n=3时，a2,2=λ

由于Bézier曲线通过控制多边形的起点p1与终点pn，所以令=p1，=pn，于是可知：

因此由式(8)~(12)可得正系数矩阵：

(1) 当n=2m,m=2,3,…时

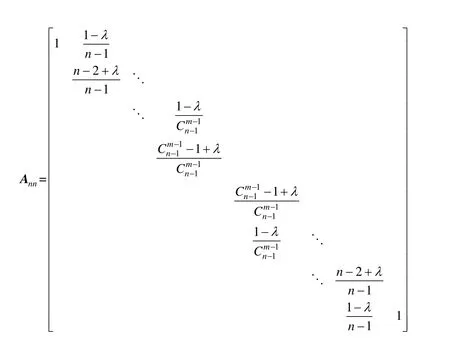
(2) 当n=2m+1,m=2,3,…时

因为矩阵中所有元素为正，所以1-≤λ≤1。

以n=6为例，A-Bézier曲线为：

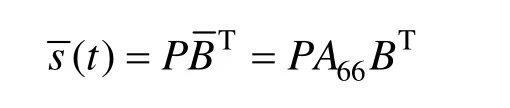
其所对应的新控制点为：

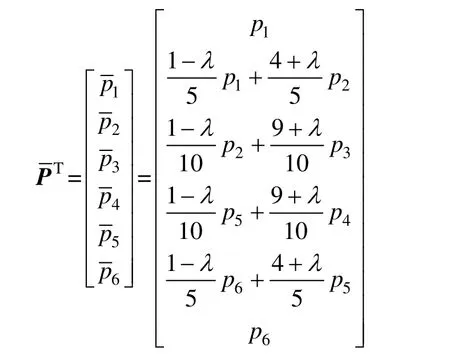
其控制多边形如图2所示：

其中虚线为新的控制多边形，通过改变参数的取值可以实现对控制多边形的调整，由于新控制点始终都是原始控制点的二点加权，所以保证了新曲线的凸包性。

图2 控制多边形

2 同阶含参A-Bernstein基函数表达式及性质

利用上述正系数矩阵可得扩展后的A-Bernstein基函数表达式：

(1) 当n=2m,m=2,3,…且1-≤λ≤1时

其中j=m+1,m+2,…,n时(t)=

(2) 当n=2m+1,m=2,3,…时，1-≤λ≤1时

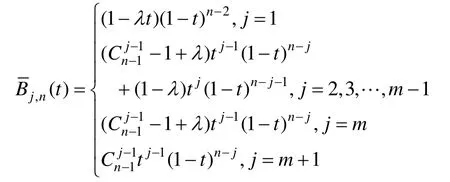
其中j=m+2,m+3,…,n时，(t)=+1-j,n(1-t)

下面给出A-Bernstein基函数的性质：

性质1.正性

(t)=ABT(t)，因为B(t)≥0,t∈[0,1]且Annnn为正系数矩阵，所以(t)≥0,t∈[0,1]。

性质2.权性

(t)=ABT(t)，因为nn且,m=1,2,…,n，所以1,t∈[0,1]。

性质3.对称性

(t)=ABT(t)，因为B(t)=B(1-t)且nni,nn-i+1,n aij=an+1-i,n+1-j,1≤i,j≤n，所以(t)=

性质4.退化性

当λ=1时，Ann退化为单位矩阵，因为所以A-Bernstein基函数退化为Bernstein基函数。

对应的A-Bézier曲线具有如下性质：

性质1.端点特性

(1) 端点位置矢量：扩展后的曲线表达式为

(2) 端点切矢量：扩展后的新控制多边形顶点矩阵为：

所以：

因此表明扩展后的曲线与首末两边矢相切，模长关系确定。

性质2.对称性

若保持控制多边形顶点的位置不变，只是把顺序颠倒，那么新Bézier曲线与原曲线重合。

性质3.凸包性

因为(t)=1,t∈[0,1]且(t)≥0,t∈[0,1]，所以有：

此式与重心的位置公式相同，分母可代表一个总质量为1的质点系，而该系统中各质点的位置矢量就为pi，质点的质量按照(t)分布，所以(t)为重心的位置。当t在[0,1]间变化时，各质点的质量也在随(t)变化，所以变化的(t)的轨迹就为对应的Bézier曲线，因此，s(t)上各点必然在pi的凸包内。

性质4.几何不变性

由于Bézier曲线具有几何不变性，Ann为正系数矩阵且具有性质1和性质2，这使得调配后的Bézier仍有几何不变性。

性质5.退化性

当λ=1时，A-Bézier曲线将退化成Bézier曲线。

3 n=6时的A-Bernstein基函数和A-Bézier曲线

当n=6，t∈[0,1]，λ∈[-4,1]时，对应的正系数矩阵Ann，A-Bernstein基函数和图像，及对应的A-Bézier曲线图像：

图3左侧为5次A-Bézier曲线，从上到下对应λ=1,0,-1,-2,-3,-4，当λ=1时退化为标准Bézier曲线；右侧为λ=1,0,-1,-2,-3,-4时的A-Bernstein基函数曲线。

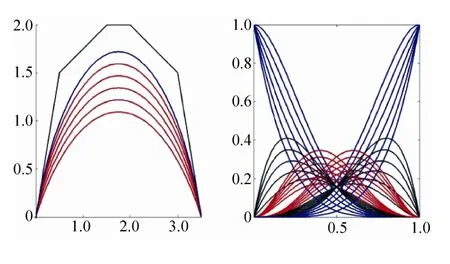
图3 5次A-Bézier曲线与A-Bernstein基函数曲线

4 正系数矩阵的调整性

4.1 添加参数

通过改变λ的范围，可以在某方向上调整A-Bézier曲线。在保持Ann的性质1,2的基础上，通过添加参数的方法，可令A-Bézier曲线在多个方向上进行调整。以n=6为例，向Ann添加参数β，可得：

当t∈[0,1]，λ,β∈[-4,1]时，对应的A-Bernstein基函数为：

可以通过对两个参数λ,β取不同的值实现曲线在多个方向上的调整，图4中虚线对应的参数分别为λ=1,β=-4和λ=-4,β=1，实现在了不同方向上的调整。

图4 曲线的含参调整

4.2 矩阵列移位

在保证Ann的性质1和性质2的基础上，通过对Ann的列元素进行移动，可实现对曲线“胖瘦”的调整。以n=6为例，令第三列元素循环下移一个单位，令第四列元素循环上移一个单位，可得：

当t∈[0,1]，λ∈[-5,1]时，对应的A-Bernstein基函数为：

如图5所示，上下为变化前后的A-Bézier曲线和A-Bernstein基函数曲线，由于移动了Ann的列元素，使得矩阵元素更加集中，从而导致了A-Bernstein基函数的更加紧凑，所以使得对应的A-Bézier曲线更加“瘦”，图6中为调整前后的Bézier曲线。

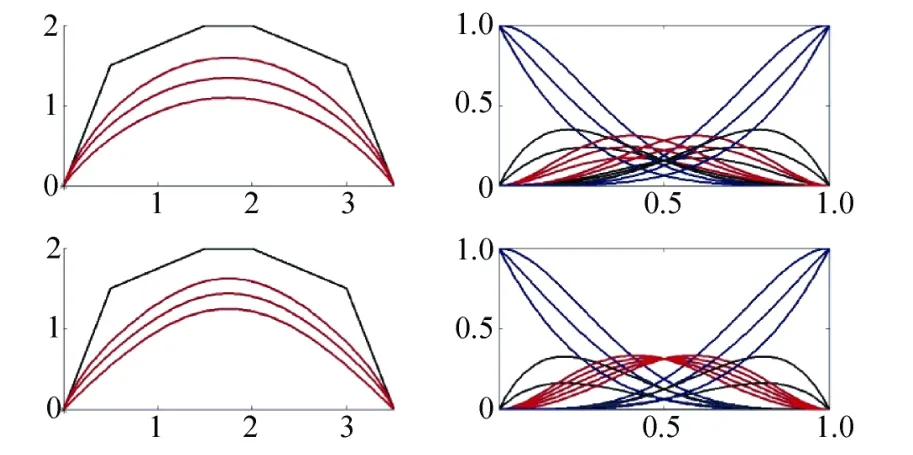
图5 矩阵元素调整前后的曲线

图6 矩阵元素调整后的曲线

5 应用实例

利用5次A-Bézier曲线绘制花瓣图形，图7为含单参的A-Bézier曲线，其中λ=-4,-3,-2,-1,0,1。图8为含双参的A-Bézier曲线，其中λ=-4,-3,-2,-1,0,1，β=1,0,-1,-2,-3,-4。图9为利用正系数矩阵的列元素位移使得A-Bézier曲线变“瘦”的实例。

图7 含单参的A-Bézier曲线

图8 含双参的A-Bézier曲线

6 结 论

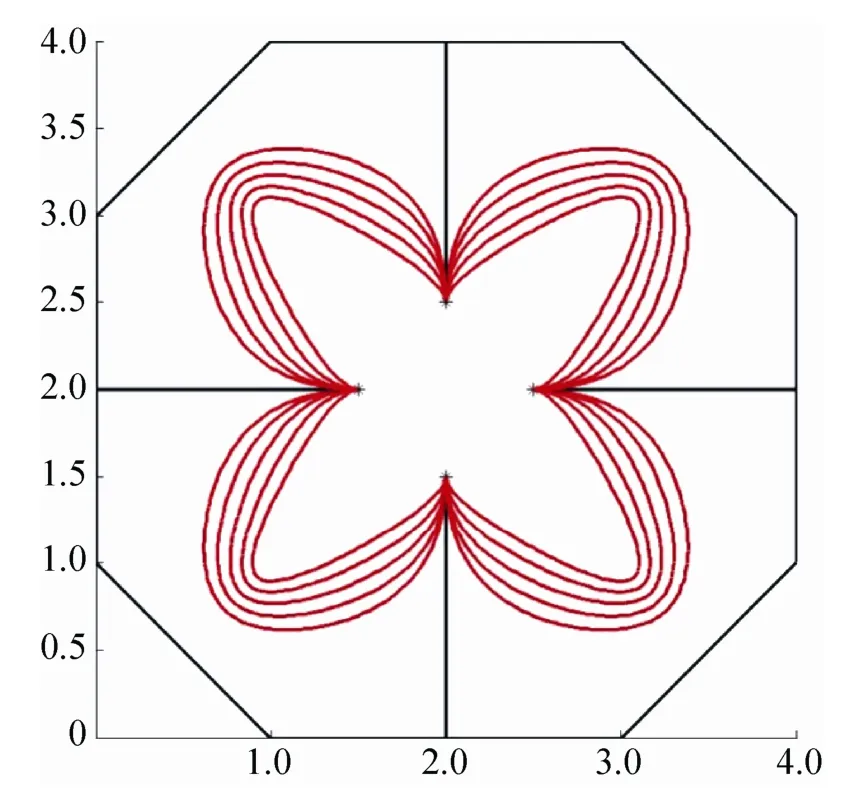
图9 矩阵元素位移后的曲线

以Bernstein多项式作为基函数的Bézier曲线曲面，凭借着其许多良好的几何性质，在CAGD，CG领域有着广泛的应用。论文以二项式的展开系数为基础，通过含参的正系数矩阵对Bernstein基函数进行调配，得到了同阶含参的A-Bernstein基函数，以及对应的A-Bézier曲线。证明了A-Bernstein基函数和A-Bézier曲线分别具有Bernstein基函数和Bézier曲线类似的性质，并且A-Bézier曲线的形状在原始控制点不变的情况下，不但可以通过形状参数进行调整，还可以通过修改正系数矩阵进行调整。最后通过举例说明了方法可行有效，在几何造型中方便于交互设计。

[1]施法中.计算机辅助几何设计与非均匀有理B样条[M].北京: 高等教育出版社,2001: 114-163.

[2]邹 静.Bézier曲线的扩展研究[D].杭州: 杭州师范大学,2012.

[3]韩旭里,刘圣军.二次Bézier曲线的扩展[J].中南工业大学学报 (自然科学版),2003,34(2): 214-217.

[4]秦新强,胡钢,张素霞.三次Bézier曲线的新扩展及其应用[J].计算机工程与应用,2008,44(2):112-115.

[5]刘小琼,杨国英.带两个形状参数的四次Bézier曲线的扩展[J].图学学报,2013,34(1): 41-45.

[6]翟芳芳.带两个形状参数的五次Bézier曲线的扩展[J].大学数学,2012,28(3): 59-63.

[7]刘 植,陈晓彦,张 莉,时 军.Bézier曲线曲面的同次扩展[J].中国科技论文在线,2011,6(10): 721-725.

[8]刘 植.Bézier曲线的扩展[J].合肥工业大学学报(自然科学版),2004,(8): 976-979.

[9]程黄和,曾晓明.带形状参数的Bézier曲线[J].厦门大学学报(自然科学版),2006,45(3): 320-322.

[10]严兰兰,宋来忠.带两个形状参数的Bézier曲线[J].工程图学学报,2008,29(3): 88-92.