对开放性教学的再认识
戴科
动手实践、自主探索和合作交流是小学生学习数学的重要方式,学生是这样,老师也是如此。苏霍姆林斯基说过:在人的内心深处有一种根深蒂固的需要,那就是希望自己是一个发现者、研究者、探索者。我校每学期开展的轮流试教活动也真正体现了实践、合作、交流、提高。上学期的轮流试教使我受益匪浅,使我对主体性开放教学由原来的“似懂”到后来的“稍懂”(在教学设计后的思考中有所体现),课程是这样设计的:
第一环节:谈预习收获
1.首先邀請两名学生相距一米站立,考查学生是否理解“间距”“间隔”“间隔数”等植树问题中的名词。
2.伸开手指,让学生通过直观形象的实物进一步理解以上名词。
3.还有什么预习收获?可能有学生会说到“间隔数+1=棵数”,由此引出对新知的探讨研究。
(设计意图:本环节主要是检查学生的预习情况,通过考察可以确定学生的基础知识,以便对新知有个很好的把握)
第二环节:探究新知
我是这样引入的:现在我们所居住的城市需要绿化,那么就要种树了,请你设计。
接着出示一道思维开放的题让学生先独立设计再同桌交流(因为学生预习过,所以学生有这种能力):在一条长20米的小路的一边等距离种树(两端都种),可以怎么种?什么是“等距离”?用线段图表示你的方法。
然后学生画线段图,种一种树,独立设计并列出算式。
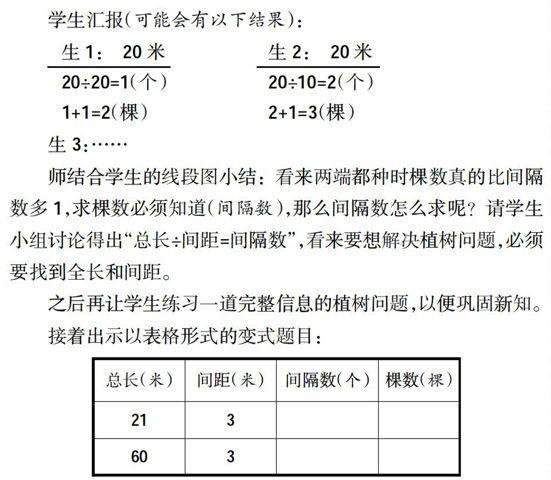
学生汇报(可能会有以下结果):
生3:……
师结合学生的线段图小结:看来两端都种时棵数真的比间隔数多1,求棵数必须知道(间隔数),那么间隔数怎么求呢?请学生小组讨论得出“总长÷间距=间隔数”,看来要想解决植树问题,必须要找到全长和间距。
之后再让学生练习一道完整信息的植树问题,以便巩固新知。
接着出示以表格形式的变式题目:
(这也是一个开放性的表格题目,先求路的一边过渡到两边都种情况)
(设计意图:这一环节是本节课的重点,本节课重点探讨在线段上植树(两端要栽)的情况中“棵数=间隔数+1”,“总长÷间距=间隔数”的关系,间隔数与棵树的关系其实也是生活中一些类似问题的关系问题,因此,本环节就是向学生渗透此类问题的思想方法、让学生发现规律,建立数学模型的过程,非常重要)
(过渡)你们真了不起,应用知识这么灵活!其实生活中有很多类似植树问题的例子,你能举出几个吗?注意和今天学习的植树问题联系起来。
(生举例)
第三环节:巩固练习及课堂作业
1.同学们在全长100米的小路两边种树,每隔5米种一棵(两端都种),一共需要多少棵树苗?
2.小明住的楼房每个楼层都有18个台阶,小明从一楼到三楼,共要走多少个台阶?
3.下课了,同学们要在门外站成4队,每隔1米站一位,四(2)班56个人需要排多远?
(设计意图:本环节意在通过不同层次的题目练习,让学生更能熟练灵活地掌握两端都种树的问题,并让学生带着问题下课以引起思考)
课后思考:整节课的教学,我努力想做到发散学生思维,学生通过小组合作、交流,自主构建植树问题的数学模型,从而体会复杂问题从简单入手的数学思想,感悟数形结合的思想,营造一份“天高任鸟飞、海阔凭鱼跃”的佳境,让每一位学生都能成为学习的主人。另外,还提到应该在第二环节的“线段图”之后,做一道有完整信息的题目,再出现表格形式的题目,这样让学生对植树问题有一个整体认识后,再建立数学模型,学生理解得可能会更加深刻。这一点我开始感觉有些不合理:本来是开放的教学,为什么还需要出现这么“规矩”的题目呢?可之后再仔细想想这样还是有必要的:因为开放的教学也是建立在有引导能力的扎实基础之上的,如果没有了“完整性”这个扶手,那么再开放性的思维题目也不容易被真正理解。
的确,通过学校的轮流试教活动可以使自己进步得更快,上课是开放的,评课是开放的,收获是无限的。
参考文献:
刘俊瑜.对应法在植树问题中的运用[J].新课程,2013(7).
编辑 王爱芳