单弹光调制傅里叶偏振光谱测量研究

张 瑞，王志斌，李 晓，陈友华，王耀利，杨 强

(1.中北大学 仪器科学与动态测试教育部重点实验室，山西 太原030051；2. 中北大学 山西省光电信息与仪器工程技术研究中心，山西 太原030051)

引言

对于地球表面和大气中的任何目标，在反射、散射和透射太阳辐射的过程中，会产生由其自身性质决定的偏振特性。通过获取目标的偏振特性可以为被观测目标提供传统方法无法获取的新信息，对所获得的信息进行综合利用，可以有效提高目标检测和识别能力。因此偏振信息获取在大气气溶胶检测、环境监测、目标识别、以及生物医学等领域具有广阔的应用前景[1-2]。光的偏振特性主要用Stokes矢量(S0,S1,S2,S3)T表示[3]，因为Stokes矢量既可以表示全偏振光，也可以表示部分偏振光和非偏振光，自然界中主要的是部分偏振光和非偏振光。因此，对Stokes矢量测量具有非常重要的意义。

弹光调制是基于弹光效应的调制器件，具有无机械振动、通光角孔径大(锥角达±50°)、受光面积大(最大为45 mm)、信号调制频率高(20 kHz～100 kHz)、适用波段宽(从紫外到红外)、机械品质因数高(≥103)等优点[4-8]。这些优点使得PEM在大视场、高灵敏度、高速度、宽光谱测量中具有无可比拟的优势。目前的弹光调制测偏振方法主要有两种：一种是通过一次测量锁相4个不同频率分量可以获得Stokes矢量，但控制操作比较复杂；另一种是通过双弹光差频调制测量，但需要加入波片。并且上述两种方法难以得到复色光的偏振光谱。针对以上测量方法存在的缺点，本文介绍一种单弹光调制器偏振光谱测量新方法，该方法对调制信号傅里叶变换得到被测光Stokes矢量中S1、S2和S3的光谱，给出该方法的理论推导，并通过仿真验证其可行性。

1 Stokes矢量

Stokes矢量是英国物理学家Stokes在研究部分偏振光时首次提出的。由于Stokes矢量既可以描述完全偏振光，也可以描述部分偏振光和非偏振光，所以在所有描述光偏振特性的方法中，Stokes矢量被广泛应用。Stokes矢量可用4个参数表示所有光的偏振状态，具体表示如下[9]：

(1)

2 原理

2.1 弹光调制器

弹光调制器是一种基于高性能弹光晶体(如熔融石英、硒化锌等)弹光效应的调制器件，利用压电晶体(如石英、压电陶瓷)在光学各向同性的物质上加以周期性变化的机械应力，使弹光晶体共振，形成应力驻波，由于弹光效应，弹光晶体出现周期性变化的双折射，因此光通过弹光调制器后其相位被调制[10]。

光通过弹光晶体两互相垂直的偏振分量的相位延迟为

δ=δ0sin(ωt+φ)

(2)

其中相位延迟的幅值为

(3)

式中：d为弹光晶体通光方向的厚度；λ为光波波长；k是与弹光晶体和压电晶体有关的系数；V0为对应驱动电路的电压峰值[11]。

2.2 单弹光调制傅里叶偏振光谱测量原理

单弹光调制傅里叶变换光谱偏振测量原理如图1所示。在测试光路中，弹光调制器(PEM)与检偏器透光轴成45°角，被测光依次通过弹光调制器和检偏器后，由探测器把调制后的光信号转化成电信号，对此电信号进行数据处理就可得到被测光的S2和S3的光谱。同理，同时转动这个装置-45°角，可测得S1和S3的光谱。具体推导如下：

图1 单弹光调制偏振光谱测量原理图Fig.1 Schematic of measured polarization based on PEM

光经弹光调制和检偏器后的Stokes矢量为[9]

(4a)

(4b)

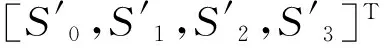
(5)

式中：δ=δ0(σ)sin(ωt)；ω为调制角频率。将(5)式代入(4)式可得，

(6a)

(6b)

由于探测器只能得到总的光强S0′和S0″，并且探测器接收到的是波数不同光的叠加，所以由(6)式可得：

(7a)

(7b)

将δ=δ0(σ)sin(ωt)带入(7)式可知，调制后的干涉信号是随时间变化的函数，并且S0(σ)调制后为直流成分，而直流成分与反演偏振光谱无关，所以省去直流分量得：

S3(σ)sin[δ0(σ)sin(ωt)]dσ

(8a)

S3(σ)sin[δ0(σ)sin(ωt)]}dσ

(8b)

又因为相位延迟幅值δ0(s)与波数σ和PEM调制最大光程差L0满足关系：

δ0(σ)=2πL0σ

(9)

将(9)式代入(8)式可得：

S3(σ)sin[2πL0σsin(ωt)]}dσ

(10a)

S3(σ)sin[2πL0σsin(ωt)]}dσ

(10b)

由(10a) 式可知，S0′(t)的正弦部分的系数为S2(σ)/2、余弦部分系数为S3(σ)/2，对S0′(t)信号进行傅里叶变换，所得结果的实数部分即为S2(σ)/2，虚数部分即为-S3(σ)/2；同理由10(b)式可知，S0″(t)的正弦部分的系数为S1(σ)/2、余弦部分系数为S3(σ)/2，对S0″(t)信号进行傅里叶变换，所得结果的实数部分即为S1(σ)/2，虚数部分即为-S3(σ)/2。通过上述推导可知，该单弹光调制器偏振光谱测量方法，可通过对调制信号傅里叶变换后的实部和虚部处理即可得到被测光Stokes矢量中S1、S2和S3的光谱。

3 仿真分析

为证明上述理论的可行性，下面用Matlab对上述理论进行仿真分析。假设被测光的波数范围为12 000 cm-1～20 000 cm-1，被测光的Stokes矢量中的S1(σ)光谱、S2(σ)光谱和S3(σ)光谱如图2所示(归一化)。

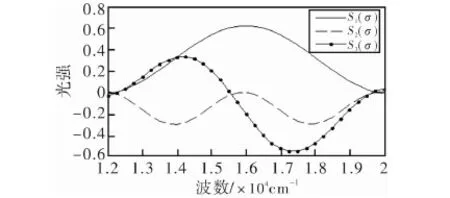
图2 S1(σ)、S2(σ)和S3(σ)原始偏振光谱Fig.2 Input S1(σ)、S2(σ) and S3(σ)

将被测光代入(10a)可得包含S2(σ)和S3(σ)的干涉信号，如图3a所示(归一化)；同理，将被测光代入(10b)可得包含S1(σ)和S3(σ)的干涉信号如图3(b)所示(归一化)。由仿真可以看出，偏振光谱的干涉信号并不是关于零光程差对称，原因主要有以下两点：一方面，由(10)式可知，此方法调制后的干涉信号不只含余弦项S1(σ)cos[2πL0σ(ωt)]或S2(σ)cos[2πL0×σ(ωt)]，同时也包含正弦项S3(σ)sin[2πL0σ(ωt)]，干涉信号为这两部分的叠加；另一方面，由于偏振光谱的权重可以为正数或零，或为负数，因此Stokes矢量中的S1、S2和S3可以为正数、零或负数。

图3 仿真干涉信号Fig.3 Simulated interferogram

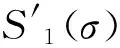
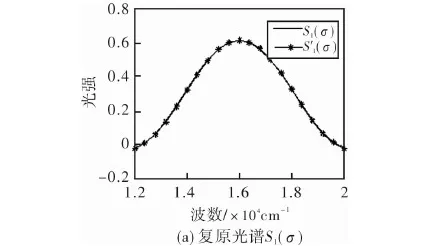
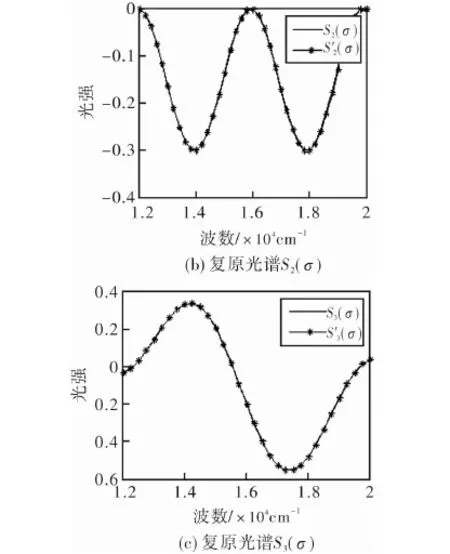
图4 复原光谱图Fig.4 Reconstructed spectra

4 结 论

通过以上分析和仿真可知，这种基于单弹光调制的偏振光谱测量方法，通过提取干涉信号傅里叶变换后的实部和虚部可获得被测光Stokes矢量S1(σ)、S2(σ)和S3(σ)的光谱。并对此方法的调制干涉信号和复原过程进行了模拟仿真,仿真结果表明该方法是正确可行的。文章的理论分析与仿真分析为该方法的进一步研究和仪器设计提供了理论基础。结合PEM的优点，该方法将在大视场、高灵敏度、高速度、宽光谱偏振测量中具有很好的应用前景。

[1] DINER D J，DAVIS A，HANCOCK B， et al. Dual-photoelastic-modulator-based polarimetric imaging concept for aerosol remote sensing[J].Applied Optics，2007，46(35)：8428-8445.

[2] 弓洁琼，詹海刚，刘大召.遥感遥测中偏振信息的研究进展[J].光谱学与光谱分析，2010，30(4)：1088-1095.

GONG Jie-qiong，ZHAN Hai-gang，LIU Da-zhao .A review on polarization information in the remote sensing detection[J]. Spectroscopy and Spectral Analysis，2010，30(4)：1088-1095. (in Chinese with an English abstract)

[3] 廖延彪.偏振光学[M].北京：科学出版社，2003.

LIAO Yan-biao.Polarization optics[M].Beijing：Science Press，2003. (in Chinese)

[4] HOUGH J H. Polarimetry techniques at optical and infrared wavelengths [J]. Current Status and Future Directions ASP Conference Series, 2005, 343: 3-14 .

[5] WANG Bao-liang, JENNIFER L. Basic optical properties of the photo-elastic modulator part I: useful aperture and acceptance angle [J]. SPIE, 2005, 5888: 436- 443.

[6] WANG Bao-liang，LEADBETTER A，ROCKWELL R R .Evaluation of a dual PEM stokes polarimeter using different signal processing methods [J].SPIE, 2005,5888:58880W.

[7] CHENG J C, NAFIE L A, ALLEN S D, et al. Photoelastic modulator for the (0.55-13)μm range [J]. Applied Optics, 1976, 15(8): 1960-1965.

[8] BADOZ J，SILVERMAN M P,CANIT J C．Wave propagation through a medium with static and dynamic birefringence：theory of the photoelastic modulator[J]．J．opt．Soc．Am．A，1990，7(4)：672-682

[9] 竺庆春，陈时胜．矩阵光学导论 [M]．上海：上海科学技术文献出版社，1991.

ZHU Qing-chun,CHEN Shi-sheng. Matrix optics Introduction[M].Shanghai:Shanghai Science and Technology Literature Press，1991. (in Chinese)

[10] CLINE R.A，WESTERVELD W B,RISLEY J S.A new method for measuring the retardation of a photoelastic modulator using single photon counting techniques[J]. Review of Scientific Instruments，1993，64(5)：2169-2174.

[11] 周军，苏桂英，李国华.光弹调制器定标新方法[J].光子学报，2001，30(1)：81-84.

ZHOU Jun，SU Gui-ying，LI Guo-hua.A new method for calibration of photoelastic modulator [J].Acta Photonica Sinica，2001，30(1)：81-84. (in Chinese with an English abstract)