插值和滤波处理技术在激光三角法测量中的应用研究

周红锋,任朴生

(临沧师范高等专科学校 数理系，云南 临沧 677000)

在精密光学测量中，光斑图像特征点区域的精确定位至关重要.如今，数字图像处理技术已经非常成熟，可以应用适当的数字图像处理技术来实现光斑图像特征点区域的定位计算，从而减小测量误差，提高测量准度和精度.

1 光斑图像的预处理

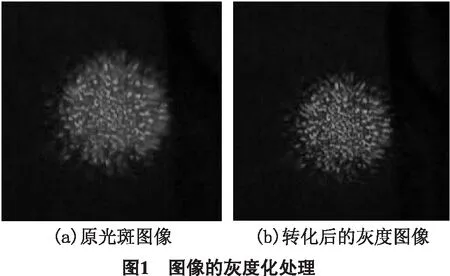
激光三角法测量小角度[1]的实验中，CCD相机采集到光斑图像是由红(Red)、绿(Green)、蓝(Blue)三基色组成的彩色图，如图1(a)所示.在彩色图中，其冗余信息(如背景、颜色信息等)和干扰信息较多(如杂散光、噪点等)，如果直接对其进行计算处理，程序开销和计算量都较大，且会影响光斑图像特征点区域定位的准确性和精度.处理过程中，为了能够有效地去噪和减少计算量，采用八叉树颜色量化算法和色彩系统变换法[2-3]把其转化为灰度图，如图1(b)所示；并尝试使用了中值滤波、均值滤波和高斯低通滤波3种方法对灰度图进行滤波和去噪处理.

2 光斑图像特征点区域的分割

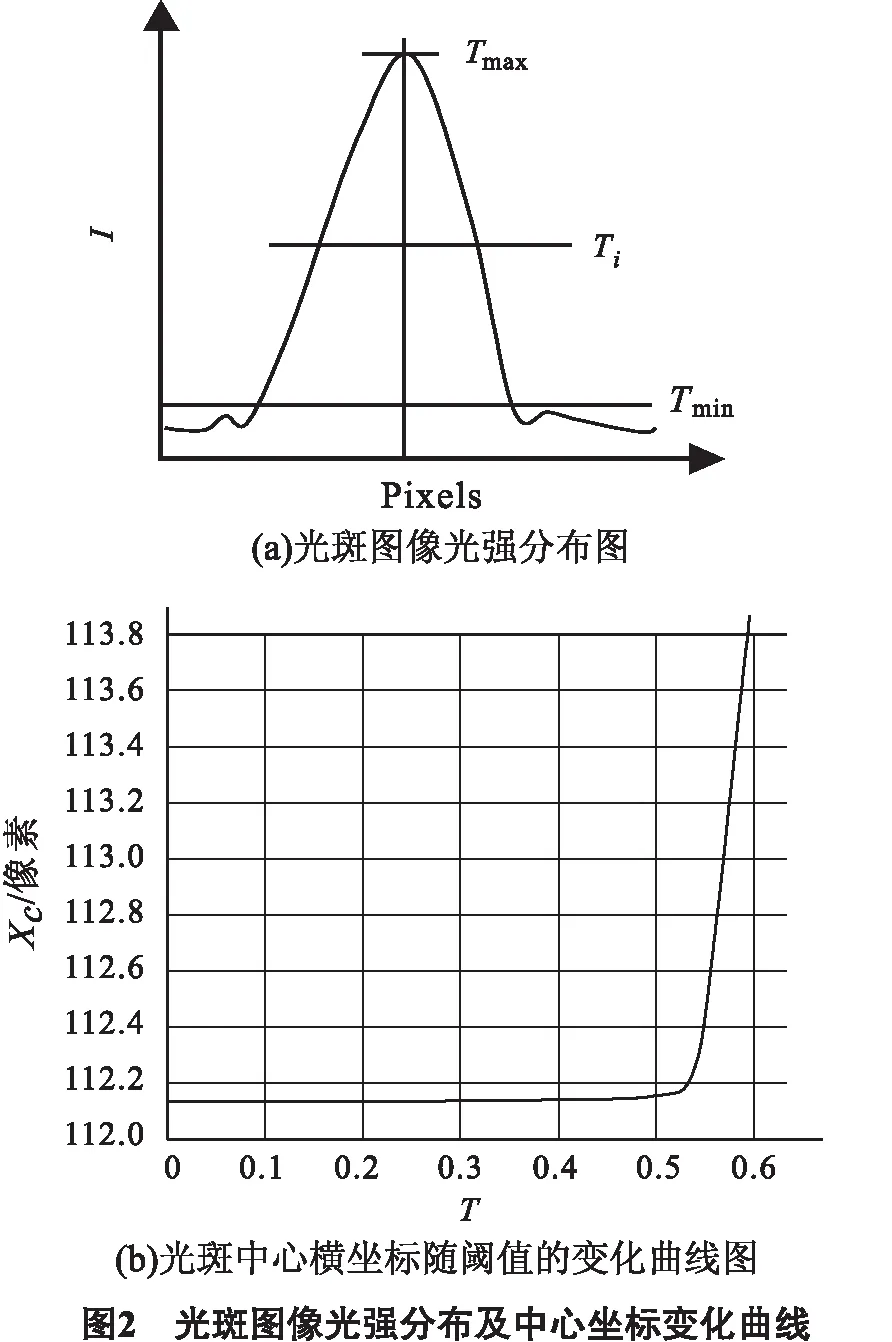
从背景中把光斑图像特征点区域分割提取出来，可以更好地对其进行定位计算.图2(a)所示是光斑图像的光强度分布图，是典型的脉冲分布，强度值较大部分是光斑特征点区域，强度值较小部分就是背景.从图中可以看出，只要选择一个合适的阈值Ti，就可以把光斑图像特征点区域从背景中分割出来.

2.1 直接阈值法分割

一般情况下，不同的阈值Ti分割得到的光斑图像，定位计算得到的其特征点区域中心的坐标数值也会不同，图2(b)是特征点区域中心的XC随T的变化曲线，T为选取的阈值与图像中最大灰度值的百分比.

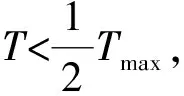
2.2 迭代阈值法分割[4-5]

为了获得较为适合的分割阈值，可以采用迭代法进行计算.其算法是：先求出图像中的最大灰度值和最小灰度值，令初始阈值为最大灰度值和最小灰度值的平均值，据此把图像分为目标和背景2组，再算出目标组的平均灰度值和背景组的平均灰度值，则又取新阈值为二者的平均值，以此循环进行计算，直到两部分的平均灰度值不再改变，此时的阈值即为最佳阈值.图3(b)是用迭代阈值法分割得到的光斑图像特征点区域.

3 光斑图像特征点区域的定位

要实现光斑图像特征点区域的精确定位，一般可采用插值或拟合2种方法来实现.插值处理方法一般分为线性插值和非线性插值2种[6].本文中使用了最近邻和双线性2种线性插值处理方法，实现特征点区域中心的亚像素定位，并且定位的速度和稳定性也有很明显的改善[7-8].

3.1 最近邻插值处理

最近邻插值是一种零阶线性插值方法，即令插值点像素的灰度值等于距离它所映射到的位置最近的像素的灰度值.这种方法是当图片插值放大时，缺少的像素通过直接使用与之最接近的原有像素的数值生成.

最近像素插值算法是一种最简单的插值算法，虽然这种算法简单，处理的速度较快，但结果通常会产生较为明显的锯齿现象，效果往往不好.若要求不高，其结果一般也可以满足要求，但若图像中包含的纹理、灰度等细微变化结构时，该方法会使图像边缘的阶梯形失真现象比较明显[9].图4(a)为经过最近邻插值处理放大后的光斑图像.

3.2 双线性插值处理

双线性插值是一种一阶线性插值方法，其算法是每个插值点的像素都是原图中4个相邻像素加权运算的结果，这样就增加了插值点和周围像素间的关联，因此这种算法很大程度上消除了锯齿现象，而且插值后的视觉效果也比较好[10].图4(b)即为用双线性插值算法(插值步长均取0.5)插值处理放大后的光斑图像.双线性插值法计算量大，但插值后图像质量高，不会出现像素值不连续的的情况.由于双线性插值具有低通滤波器的性质，使高频分量受损，所以可能会使图像轮廓在一定程度上变得模糊，即边缘模糊效应会增强.

4 结果与分析

实验中，对同一幅光斑图像在3种常用滤波处理情况下，其中心定位的计算结果进行对比，如表1所示.XC、YC光斑图像中心的坐标值，结果保留到小数点后2位有效数字，平均值的标准差保留到小数点后3位有效数字(单位均为像素).

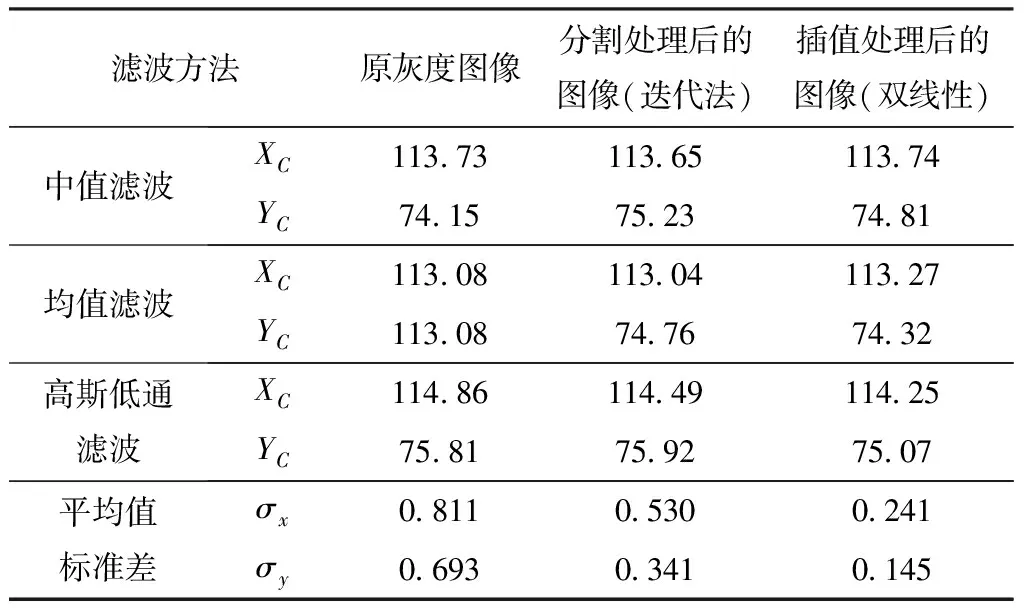
表1 同一幅光斑图像在3种滤波处理后结果 像素

从表1可以看出，原灰度图通过3种滤波处理后的中心坐标的标准偏差为0.8个像素左右，而经过数字图像处理后，其中心坐标的标准偏差逐渐减小.采用迭代法分割处理后其标准偏差为0.5个像素左右，而采用迭代法分割和双线性插值两次处理后,其标准偏差为五分之一个像素左右，定位精度大大提高，而且定位的速度和稳定性也得到了很大改善.因而，该方法在激光三角法测量的光斑图像处理中具有一定研究意义和应用前景.

参考文献:

[1] 周红锋，王东云，黄锑儒，等.激光三角法测量小角度的测量模型和光路设计研究[J]. 云南民族大学学报：自然科学版,2008,17(3):277-279.

[2] 钟志光，卢君，刘伟荣. 数字图象处理实例与解析[M].北京：清华大学出版社,2003：62-93.

[3] GONZALEZ R C, WOODS R E. 数字图像处理[M].2版.阮秋琦,译.北京: 电子工业出版社, 2002:175-176.

[4] 钟志光,卢君,刘伟荣. Visual C++.NET 数字图象处理实例与解析[M].北京：清华大学出版社,2003:371-372.

[5] CASTLEMAN K R. Digit image processing[M]. Prentice Hall, 1996: 186-213.

[6] 于起峰. 基于图像的精密测量与运动测量[M].北京：科学出版社,2002:132-13.

[7] 湛廷政,吕海宝. CCD细分技术方法研究及应用[J].光学学报，2002，22(11): 1395-1399.

[8] LI Y S, YOUNG T Y, MAGERL J A. Subpixel edge detection and estimation with a microprocessor-controlled line scan camera[J]. Industrial Electronics, IEEE Transactions on, 1988, 35(1): 105-112.

[9] MATSUZOE Y, TSUJI N, YOSHIZAWA T. Error dispersion algorithms to improve the precision of angle detection for the optical encoder[C]//International Symposium on Optical Science and Technology. International Society for Optics and Photonics, 2000: 234-241.

[10] 王建民, 浦昭邦, 刘国栋. 提高图像测量系统精度的细分算法的研究[J]. 光学精密工程, 1998, 6(4):44-49.