比较BP神经网络和RBF神经网络在基金净值预测中的应用

何树红，吴 迪，张月秋

(1.云南大学 经济学院，云南 昆明 650091；2.云南大学 数学与统计学院，云南 昆明 650091)

证券投资基金是一种介于股票和债券之间，受大众欢迎的投资工具，它既能获得较高的收益，又能分散风险，并使得投资人的资产可以得到相对的保证.由于股票市场表现疲软，收益相对稳定的基金市场在中国迅速崛起，基金投资已成为人们在证券市场获益的一个重要手段.与其他证券相比，基金具有风险低，流动性好的特点，是存放现金的理想工具.近年来，投资基金在全球金融市场中的发展十分迅猛,人们对基金的关注程度不断提高,基金投资也得到更多投资者的青睐.伴随着基金热的出现，基金的发行规模逐年增大，基金投资者也越来越多，投资基金的收益与风险并存.为了获取更高的投资收益，就必须冒较大的风险，人们迫切需要一种有效的基金净值预测方法，最大限度地增加投资收益，降低风险成本.因此，对基金净值预测模型的研究，具有极其重要的意义[1]. 基金市场的活跃程度影响基金净值的变动，基金市场内部因素种类繁多，基金净值由于受到财政、经济、社会风险等多重因素的影响，具有较强的波动性.与传统的线性模型相比，神经网络模型对于拟合具有明显非线性特征的基金，效果更为显著[2].

本文主要以“华夏成长基金”为例进行实证研究分析.“华夏成长基金”是中国走势较好的混合型基金，具有股债混合，攻守兼备等特点.一般来讲，混合型基金持股比例在75%～85%，债券持仓在25%～15%.所以这种基金在上涨中可以提高持股比例，获得较高收益；在下跌中，可以降低持股比例，增加债券比例，减少损失.对混合型基金净值走势的判断可直接影响基金投资人对基金的决策.因此，预测混合型基金更能准确地反映基金市场的普遍情况.

BP神经网络具有很强的非线性拟合能力，可映射任意复杂的非线性关系，并且学习规则简单，便于计算机实现，但其仍然存在学习速度慢、容易陷入局部极小点而无法得到全局最优解等缺点；相比于BP神经网络，RBF神经网络的拓扑结构更加紧凑，且结构参数可实现分离学习，克服了BP神经网络学习速度慢的缺点，提高了神经网络的学习泛化能力，具有更高的预测精度.

1 基金净值的主要影响因素

1.1 基金份额资产净值

基金资产净值代表基金的实际价值，即在某一估值点上，基金资产的总市值扣除负债后的余额.基金份额资产净值是指每一基金份额代表的基金资产净值.

1.2 基金资产份额累计净值

基金资产份额累计净值是指基金最新净值与成立以来的分红业绩之和，体现了基金所取得的累计收益，能准确地反映基金业绩的真实水平.

基金份额累计净值=基金份额净值+基金成立后份额的累计分红金额.

1.3 基金持股集中度

基金持股集中度可以间接地反映基金在股票投资中的风险，持股集中度越高，说明基金在十大重仓股的投资越多，基金的风险越高.持股数量越多，基金的投资风险越分散，风险越低.

1.4 基金持仓行业集中度

基金持股集中度可以间接地反映基金在股票投资中的风险，持股集中度越高，说明基金在十大重仓股的投资越多，基金的风险越高.持股数量越多，基金的投资风险越分散，风险越低.

1.5 基金成交额

基金成交额表示已成交的基金金额的总数.

1.6 基金平均涨跌幅

1.7 居民价格消费指数

居民价格消费指数是反映与居民生活有关的产品及劳务价格统计出来的物价变动指标，通常作为观察通货膨胀水平的重要指标.

1.8 基金可分配收益

基金可分配收益指在某一时点上基金可实际用于向投资者分配的收益.

2 基金净值预测模型原理

2.1 BP神经网络

BP神经网络是一种按误差逆传播算法训练的多层前馈神经网络,其基本原理是利用输出后的误差来估计输出层的直接前导层的误差，再用这个误差估计前一层的误差，如此一层一层地反传下去，就获得了所有其他各层的误差估计. BP算法中神经元所用的激活函数必须处处可导，一般都是用Sigmoid函数.一个三层BP网络如图1所示.

2.2 BP神经网络的学习算法

BP神经网络以梯度下降算法为基础，在学习过程中不断地调整权值和阈值,使得实际输出值与输出期望值的误差达到最小.使用S型激活函数时，BP网络输入与输出的关系为：

输入：net=x1w1+x2w2+…+xnwn；

(1)

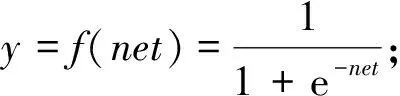
(2)

(3)

(4)

神经网络的学习过程如图2.

2.3 RBF神经网络

RBF神经网络,属于前向神经网络类型,它能够以任意精度逼近任意连续函数.RBF神经网络由三层组成，包括输入层、隐含层和输出层，隐含层的神经元数目由具体问题的情况而定.输入层节点只传递输入信号到隐含层，隐含层节点由像高斯函数那样的辐射状作用函数构成，而输出层节点通常是简单的线性函数.RBF神经网络结构如图3所示.

2.4 RBF神经网络

RBF神经网络学习算法需要求解的参数有3个：基函数的中心、方差以及隐含层到输出层的权值.根据径向基函数中心选取方法的不同，RBF网络有多种学习方法，本文将采用自组织选取中心的RBF神经网络学习方法，其学习算法如下：

RBF网络中常用的径向基函数是高斯函数，因此RBF神经网络的激活函数为：

(5)

网络的输出为：

(6)

式中，p为样本总数；h为隐含层的结点数.

设d是样本的期望输出值，那么基函数的方差可表示为 :

(7)

2.5 BP神经网络和RBF神经网络的比较

尽管RBF网络的输出是隐单元输出的线性加权和，学习速度加快，但并不等于径向基神经网络就可以取代其他前馈网络.这是因为径向基神经网络很可能需要比BP网络多得多的隐含层神经元来完成工作.

BP神经网络和RBF神经网络的区别具体表现在：①BP神经网络是全局逼近的多层前馈式输出网络，而RBF神经网络是局部逼近的三层结构网络；②BP网络使用sigmoid()函数作为激活函数，这样使得神经元有很大的输入可见区域，而RBF网络使用径向基函数(一般使用高斯函数)作为激活函数，神经元输入空间区域很小，需要更多的径向基神经元；③进行网络训练时，BP网络一般采用基于最快梯度下降原理的误差逐层回馈的训练方法，而RBF网络大都采用最小二乘法或者递推最小二乘法.

3 实证分析

3.1 数据收集与处理

采用2010年6月18日至2012年12月31日共120周的华夏成长基金12个指标集为样本数据.这12个指标集为：前周基金份额资产净值(x1)，上周基金份额资产净值(x2)，本周基金份额资产净值(x3)，前周基金资产份额累计净值(x4),上周基金资产份额累计净值(x5)，本周基金资产份额累计净值(x6)，基金持股集中度(x7)，基金持仓行业集中度(x8)，本周基金成交额(x9)，本周基金平均涨跌幅(x10)，居民价格消费指数(x11)，本周单位基金可分配收益(x12).

由于上述所选数据的取值范围不同，为了消除量纲级别，更加快速的收敛，分别运用(8)式和(9)式对数据进行归一化和反归一化处理：

(8)

(9)

3.2 训练学习方法

采用时间移动仿真法，输入层有11个变量，输出层有1个变量，用前105周数据作为训练集，预测第106周基金资产净值，然后向前移动1周，重复该过程进行学习训练，预测第107周基金资产净值，直到120周结束，共进行15次学习训练.

3.2.1 BP神经网络训练

为使训练结果更为精确，采用BP网络的改进函数traincgf进行训练，将tansig作为输入函数，purelin作为输出函数，学习速率设置为0.05，动量系数设置为0.9，最大训练次数 3 000 次，目标误差0.01，通过调整隐含层神经元的数目，降低训练结果的平均误差，经过多次训练比较，得出当隐含层神经元数目为10时，平均误差最小.

3.2.2 RBF神经网络训练

为了更有效地进行神经网络设计，径向基函数网络逼近函数时，采用newrb函数自动增加网络的隐含层神经元数目，直到均方差满足精度或者神经元数目达到最大为止.初始化网络的训练参数，误差值为0.01，散步常数为l，显示频率为1，隐含层的最大神经元数为12个.

3.2.3 实验结果与分析

2种神经网络模型对基金预测的结果及误差如表1所示.

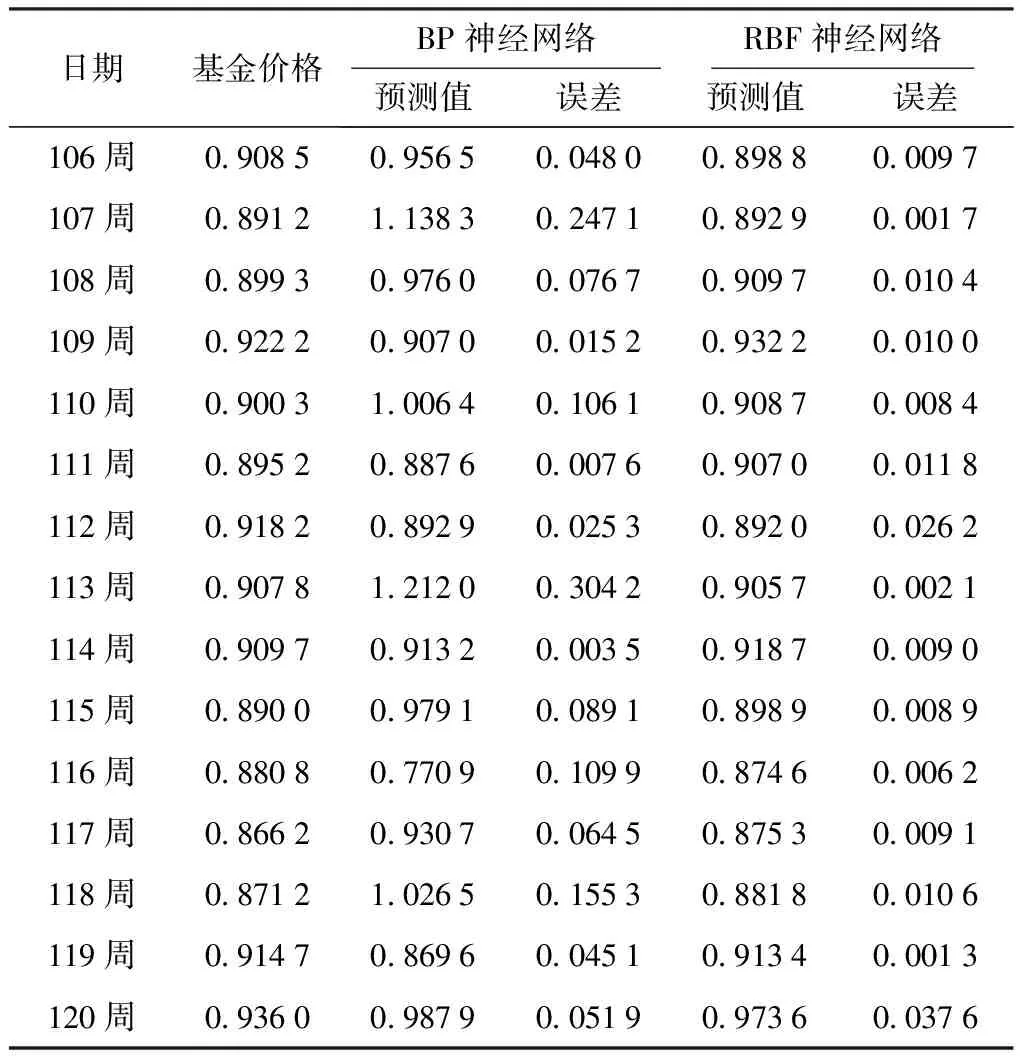
表1 预测结果及误差

2种方法的预测值和真实值的曲线比较，如图4、5所示.

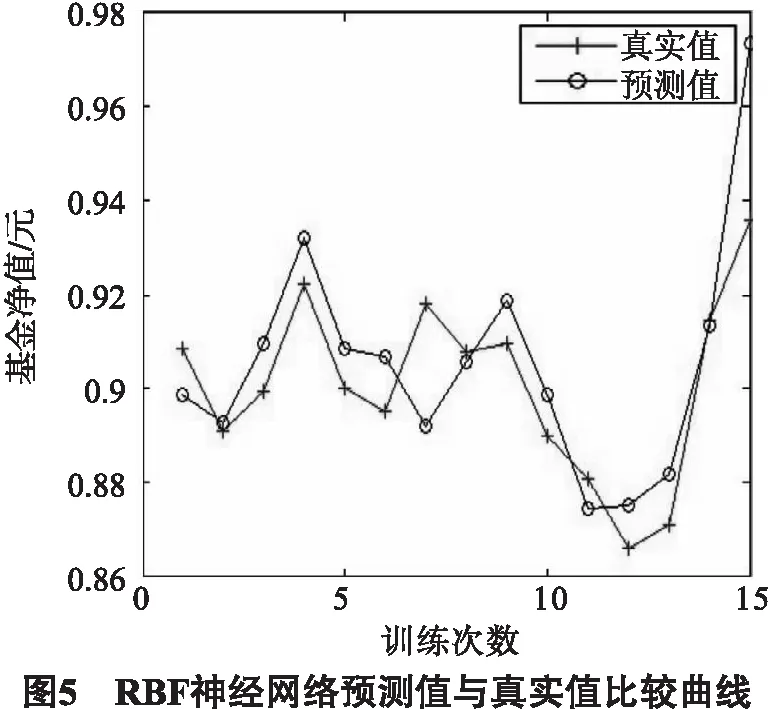
由上述结果可知，BP神经网络虽然可以大致预测基金净值的走势，但是预测结果上下浮动较大，拟合效果不理想，而RBF神经网络的平均误差值仅为0.010 9，且收敛速度快，较BP神经网络而言能够更为准确地预测基金价格.

4 结语

本文将BP神经网络和RBF神经网络同时应用于基金净值预测中，虽然BP神经网络在现实中应用广泛，但是由于其收敛速度慢、网络学习不稳定等因素，影响了基金价格的预测准确度.RBF神经网络比BP神经网络有更好的收敛速度和更高的预测精度，是一种值得推广的基金价格预测模型.

参考文献:

[1] SILVA F M, ALMEIDA L B. Speeding up backpropagation[J]. Advanced Neural Computers, 1990, 92: 151-160.

[2] CHIANG W C, URBAN T L, Baldridge G W. A neural network approach to mutual fund net asset value forecasting[J]. Omega, 1996, 24(2): 205-215.

[3] YAN H, LIU W, LIU X, et al. Predicting net asset value of investment fund based on BP neural network[C]//Computer Application and System Modeling (ICCASM), 2010 International Conference on. IEEE, 2010, 10: V10-635-V10-637.

[4] LIN H S, CHEN M L, TONG C C, et al. Using grey and RBFNN to predict the net asset value of single nation equity funds-a case study of Taiwan, US, and Japan[C]//Grey Systems and Intelligent Services, 2007. GSIS 2007. IEEE International Conference on. IEEE, 2007: 892-897.

[5] DENG J L. Grey differential equation[J]. The Journal of Grey System, 1993, 5(1): 1-14.

[6] 王波.基于神经网络的投资基金周净值预测[J].上海理工大学学报，2007(3):227-230.

[7] HAYKIN S.神经网络原理[M].北京：机械工业出版社，2004.

[8] 丛爽.面向MATLAB工具箱的神经网络理论与应用[M].合肥：中国科学技术大学出版社，2009.

[9] 刘斐弘.神经网络在股票价格预测中的应用[J].时代金融， 2012(5)：241.

[10] 穆云峰. RBF神经网络学习算法在模式分类中的应用研究[D]. 大连：大连理工大学，2006.

[11] 施彦，韩力群，廉小亲.神经网络设计方法与实例分析[M]. 北京：北京邮电大学出版社，2009.