多径干扰下GPS弱信号跟踪算法研究
卫 洁,范胜林,周 超,刘建业
(南京航空航天大学 导航研究中心,江苏 南京 210016)
随着GPS的运用越来越广泛,其适用范围已经到了一些复杂环境中,例如山地、森林或是一些大都市.在北京、上海、香港这些地区,高楼大厦鳞次栉比,绿化带随处可见,遮挡物也比比皆是.在这类环境下,GPS的信号发生严重衰减,伴随而来的,是多径等其他一系列问题.而事实上,目前民用的GPS传统接收机在信号的载噪比下降到35dB的时候性能就会变得很差甚至完全失效,这就极大地限制了GPS接收机的应用范围[1],所以研究GPS接收机在具有严重多径干扰下的性能提升是非常有必要的.
1 多径误差分析
在信号的跟踪阶段,首先利用本地产生的一个复现载波与输入信号相乘,从而剥离载波,然后再与本地产生的复现码进行相乘,进而实现伪码剥离[2].而多径信号的存在,对于载波环路和码环路都存在影响,对码环跟踪的影响远大于载波跟踪的影响[3],因此考虑在码环中进行多径抑制.码环采用延迟锁定环(DLL)进行信号跟踪,其结构如图1所示.
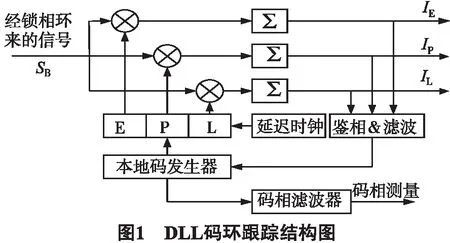
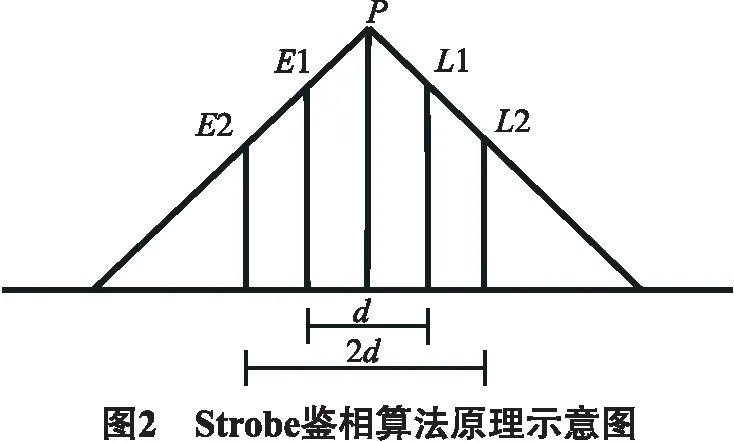
由图1可知,本地发生器会产生3种码:即时码P;超前码E;滞后码L.其中,早迟码的间距为d,超前码(E)比即时码(P)超前d/2的间隔,滞后码(L)比即时码(P)落后d/2的间隔.E、P、L码同时被送入相关器,并且与SB做相关累加运算,得到IE,IP,IL,再进入码环鉴相器进行鉴相跟踪.Strobe鉴相器算法如图2所示.
传统早迟码(EML)鉴相算法和Strobe鉴相算法如式(1)所示[4-5].
DEML=Narrow(d)=E1-L1×DStrobe=2Narrow(d)-Narrow(2d)=2(E1-L1)-(E2-L2).
(1)
式中,Narrow用来表征窄相关的鉴相函数,E1、L1、E2、L2分别为间距为d和2d的早码相关值和迟码相关值.
对EML算法和Strobe算法进行误差输出分析,得到误差包络示意图如图3.

由图3可知,Strobe算法相较于传统EML算法有了很大的改善,特别是在原来多径误差最大的时候得到了结果为0的误差输出.相同d值时的最大误差是相同的,不同的d值在包络的起始处和结束处都是重叠的.
2 σ-Strobe鉴相算法
2.1 修正因子的确定

在进行多径分类的时候,相关间距为d时,通常将多径延迟小于d的信号叫做短多径信号.在传统的鉴相器中,由于没有用到P的相关值,在进行改进的过程中,考虑结合相关函数的形态,分析其内部多径信息,利用P值,增加一个修正因子σ,取为P与实际峰值之间的误差,将误差加入鉴相器进行修正,从而增强鉴相器对短多径的抑制[6-7].对叠加后的相关函数进行研究和分析,在同相多径的情况下,考虑2种情况,即P和L1在同一条直线的情况,以及L1和L2在同一条直线的情况,分别进行σ的求解;在反相多径情况下,依旧考虑2种情况,即P和E1、E2都在同一条直线上,L1和L2不在同一条直线上,以及L1和L2在同一条直线上.同相多径的示意图如图4(a)所示,图4(b)为即P和L1在同一条直线的情况的放大示意图.将P,E1,E2,L1,L2表达如下:
P=-a(σ-1)+b(σ+1-Δτm)=(-a+b)σ+a+(1-Δτm)b;
(2)
E2=(a+b)(σ-d)+a+(1-Δτm)b,L2=-(a+b)(σ+d)+a+(1+Δτm)b.
式中,假设a,b分别表示直达信号与多径信号的斜率,Δτm为多径误差延时.经过线性组合,可以得到σ的表达式为:
(3)
由式(3)可知,可将Strobe鉴相器修正为:
(4)
下面,再来确定临界点D所对应的Δτm值.由x=Δτm(图4中CD段),x=Δτm-0.2(图4中DE段),能够得到:
(5)
由式(5)可知,在同相多径下,σ的应用范围大小取决于短多径幅值相对直达信号的幅值衰减,并且短多径幅值衰减得越厉害,σ的应用范围就越大.
2.2 σ-Strobe应用范围确定
用与2.1节中类似的方法分析另外3种情况可知,都不能使用新的鉴相器进行鉴相.同相多径的第2种情况下,将P,E1,E2,L1的表达式代入第1种情况下的修正因子σ,得到:
(6)
因此,在此情况下是不能够进行误差修正的.所以这种情况下只能使用原有的鉴相器算法进行码相位鉴相.如果属于这种情况,可以发现此时,E1-L2=L1-L2.因此,可以将它作为这种情况下,鉴相器选择的判别标准.
反相多径的时候,不管是第1种情况,还是第2种情况,将P,E1,E2,L1的表达式代入同相多径第1种情况下的修正因子σ,可以得到:
(7)
因此,在反相的情况下,对于加入了修正因子的情况,可以不予理会.
3 EKF弱信号载波跟踪环设计
3.1 基于相关值输出的EKF载波跟踪结构
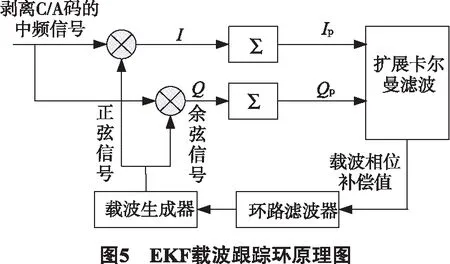
从改进后的码环鉴别器的表达式,可以看出,鉴相的过程并没有运用到Q路的输出,这就对载波跟踪的要求有所增高.而需要跟踪的信号,又是带有多径干扰的弱信号,因此,不得不考虑噪声对跟踪产生的影响,因此,在这里考虑扩展卡尔曼滤波(EKF)算法,来进行载波环路的鉴相工作[8].使用EKF算法的时候,略去了原有跟踪环路的鉴相器环节,用EKF代替,其结构图如图5所示.
3.2 基于相关值输出的EKF载波跟踪建模
由图5可知,对EKF载波跟踪系统进行建模的时候,将环路的相关积分输出IP和QP作为系统观测量,定义载波的状态量为:

(8)
式中,Δθ为本地载波与真实载波的相位差;ω为输入载波的频率;a为输入载波的频率变化率.很明显可以看出,观测量和状态量为非线性关系.
根据建模时所选的状态量和观测量进行分析,所建模型的态方程为
(9)
式中,ΔT为积分累计时间;Wn为高斯白噪声序列,其方差Q由3部分组成[9-10],如下式:
(10)
因为IP和QP为观测量,它们是环路积分值,进一步得到跟踪模型的测量方程:
(11)
式中,A表示信号幅值;D(t)为导航数据;R(Δτ)为C/A码片自相关函数;N为噪声.
可以得到观测矩阵:
(12)
(13)
经过上面的建模过程,可以得到模型的状态方程和测量方程,将它们代入到扩展卡尔曼滤波方程当中,可以得到需要估计的状态量,进而进入到环路滤波的过程中去,改善了弱信号跟踪的性能.将EKF与第2节的算法结合使用,形成新的σ-Strobe-EKF跟踪算法.
4 仿真实验与分析
4.1 EKF算法弱信号载波跟踪环仿真
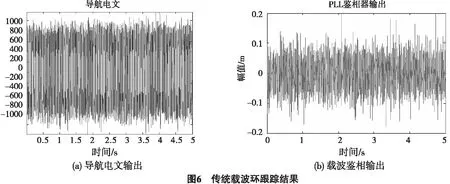
基于载噪比为38 dB的弱信号,分别针对原有的载波跟踪环路和EKF载波跟踪算法进行弱信号的跟踪仿真,跟踪总时间为5 s,跟踪结果如图6~7所示.图6(a)和图7(a)分别为2种算法解调得到的导航电文,说明跟踪成功.图6(b)和图7(b)分别为2种算法的鉴相误差输出.对比图6(b)和图7(b)可知,EKF载波跟踪环路对于弱信号的跟踪有良好的跟踪效果,比原始的二阶滤波具有更平滑的鉴相误差输出.
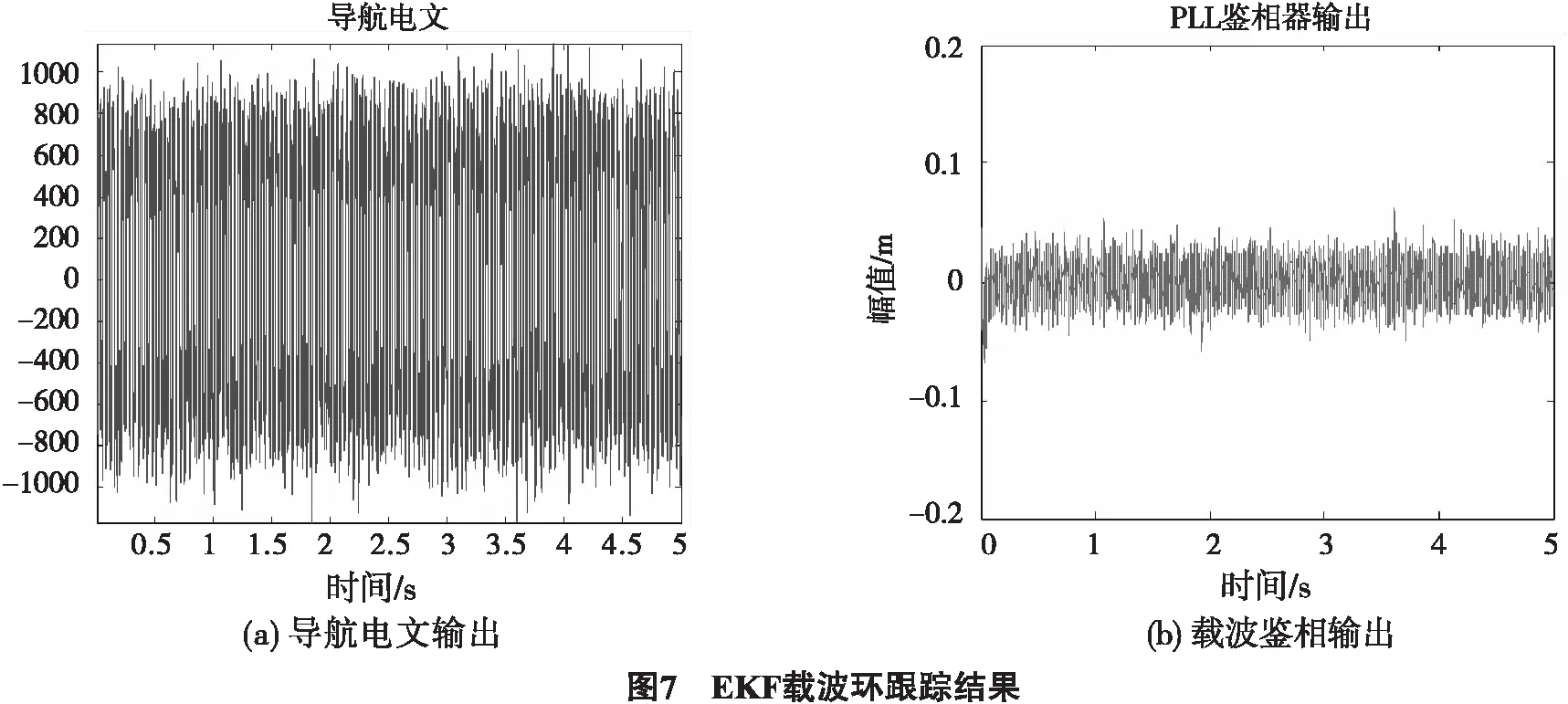
4.2 σ-Strobe-EKF跟踪算法仿真
基于44dB的弱信号,取早迟码相关间隔d=0.2,加入延迟时间为0.18 chip(约为53 m)的多径信号,信号幅值取直达信号幅值的0.5倍,跟踪时间为5 s,分别对Strobe-EKF和σ-Strobe-EKF的跟踪环路进行对比仿真,取跟踪环路中的码相误差为衡量标准,仿真结果如图8~9 所示.

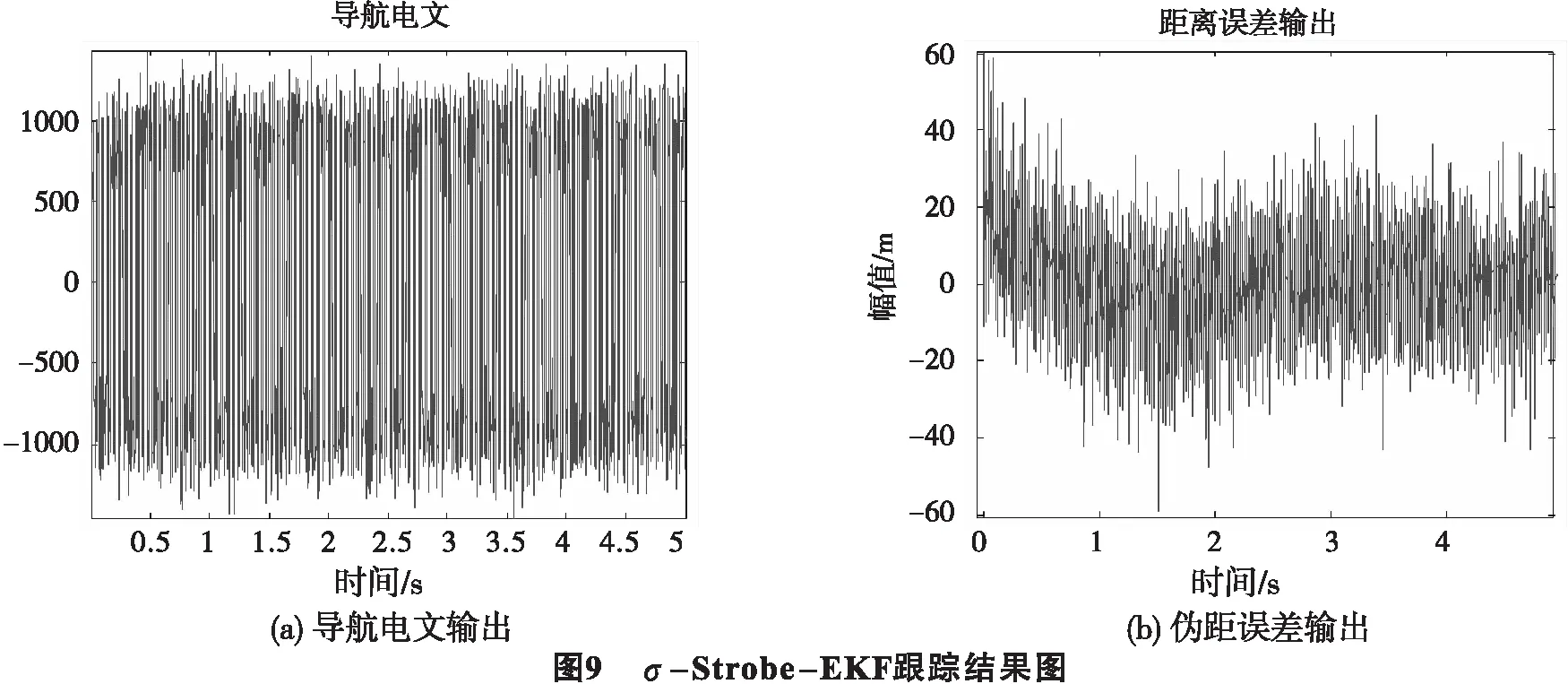
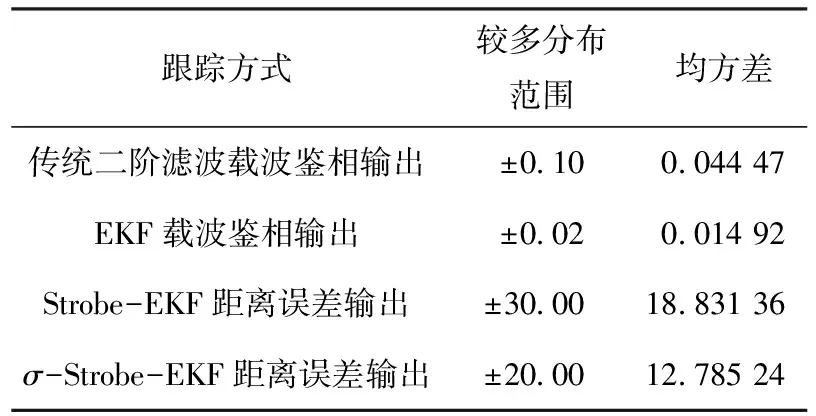
表1 不同跟踪方式下载波和距离误差输出数值分析
由图8(a)和图9(a)可知,带有多径的弱信号信号被成功跟踪.通过对比图8(b)和图9(b)中DLL鉴相误差的距离输出可知,在使用了σ-Strobe-EKF算法后,对短多径的抑制性能有了显著的改善.
为了更好的定性地体现跟踪性能,列出表1,分析不同跟踪方式下载波和码环鉴相输出数值.由均方差数值分析可知,在抑制短多径上,使用了EKF后,载波跟踪误差有了明显的改善.而在增加了修正因子的σ-Strobe-EKF算法后,码环跟踪误差也得到了抑制,能够有效地抑制多径信号带来的跟踪误差.
5 结语
从多路径误差对现代GPS系统的影响看,它已然成为了误差的主要来源.本文以跟踪环路为研究背景,分别在码环Strobe鉴相器中加入修正因子,在载波环中用EKF替代了原有的二阶滤波环路,将两者结合起来成为σ-Strobe-EKF跟踪算法,进行带有多径干扰的弱信号的跟踪.仿真结果表明,改进后的跟踪算法确实起到了作用,载波跟踪性能和码环跟踪精度都有所提高,一定范围内的短多径得到了抑制.
参考文献:
[1] KAPLAN E D, HEGARTY C J.GPS原理与应用[M].2版,寇艳红,译.北京:电子工业出版社, 2012.
[2] BORRE K, AKOS D.A software defined gps and galileo receiver: single-frequency approach[C]// ION GNSS.CA :Long Beach, 2005: 13-16.
[3] KAINDL K, NIKLASEH N.Improving path separation in a multipath environmentby applying norlinear estimation theory[C]//Proceedings of the institute of Navigation National Technical Meeting.US:Portland,2002:472-476.
[4] 纪元法, 施浒立,孙希延.一种Strobe相关器及其多径抑制性能研究[J].宇航学报.2007, 28(5): 1094-1099.
[5] RAY J K, CANNON M E.Characterization of GPS carrier phase multipath[C]//Proceedings of the ION National Technical Meeting 1999.US: Salt Lake City, 1999: 132-141.
[6] ZHANG Z, LAW C L, WAN G E.Fine delay estimation technique under multipath[C]// ION GNSS.CA :Long Beach,.2004,9:1131-1137.
[7] 宋嘉吉.GPS接收机多径抑制技术的研究与实现[D].南京:东南大学, 2010.
[8] 梁前浩.GPS中频信号仿真与微弱信号捕获、跟踪方法研究[D].北京:北京交通大学, 2008.
[9] PSIAKI M L, JUNG H.Extended Kalman filter methods for tracking weak GPS signals[C]// Proceedings of ION GPS 2002.US:Portland, 2002,9: 24-27.
[10] LIAN P.Improving tracking performance of PLL in high dynamic applications[D].CA: Calgary University, 2004.

