基于He-变分方法求弱色散解非线性波动方程的孤子解
白 秀, 杨培凤, 额尔敦其其格
(1.呼和浩特民族学院 数学系,内蒙古 呼和浩特 010051;2.内蒙古建筑职业技术学院 公共教学部,内蒙古 呼和浩特 010070)
欧朝芳等[1]讨论了传输线中非线性效应所引起的波形的变化, 并建立非线性和色散两种效应同时存在时的波动方程:
(1)
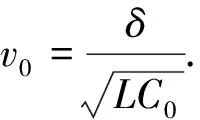
该文献中,分析了波在非线性无色散传输线和非线性有色散传输线中的传播情况,得出了非线性效应和色散效应关系的结论,同时,利用行波法求得了方程的孤波解[1].岳萍等[2]应用影射法求解此传输线中弱色散解非线性波动方程得到了孤波解和椭圆函数解,郭鹏等[3]应用试探函数法、Sine-Cosine 方法[4]求得了非线性传输线方程(1)的解.
He-变分方法[5-6]具有既简单又直接的特性,它基于He-半逆解法[5],建立一种巧妙的变分泛函,进而构造非线性偏微分方程(组)的孤立子解等精确解.该方法曾被成功应用到求解Benjanmin One方程[9]和吸孤子方程[10]等方程的孤子解中.本文从文献[6-11]得到启示,利用变分方法对非线性传输线方程(1)进行求解,成功推出该方程几种不同形式的孤子解.
1 利用变分方法求解非线性传输线方程的求解
设行波变换为u(x,t)=u(ξ),ξ=kx-λt,对方程(1)进行行波约化,得到
(2)

(λ2-α)u-bλ2u2-βu″=0.
(3)
再利用半逆解法,可得到(2)式的变分公式
(4)
(5)
1.1 情形1
设(1)的孤子解为:
u(ξ)=ptanh2(qξ).
(6)
将(6)代入变分公式(4)中,得到双参数p、q的函数:
(7)
对讨论(7)的稳定性,建立联立方程组:
(8)
(9)
然后,求解上述方程组中的(8)和(9)式,得到参数p、q的取值如下:
(10)
(11)
从而得到原方程的孤子解:
(12)

1.2 情形2
设(1)的孤子解为:
u(ξ)=psech[qξ]·tanh2(qξ).
(13)
将(13)代入变分公式(4)中,得到双参数p、q的函数:
(14)
讨论(14)的稳定性,建立联立方程组:
(15)
(16)
然后,求解上述方程组,得到参数p、q的取值如下:
(17)
(18)
从而得到原方程的孤子解:
(19)
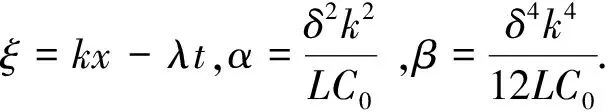
1.3 情形3
设(1)的孤子解为:
u(ξ)=psech2[qξ]·tanh(qξ).
(20)
将(20)式代入变分公式(4)中,得到双参数p、q的函数:
(21)
讨论(21)的稳定性,建立联立方程组:
(22)
(23)
然后,求解上述方程组,得到参数p、q的取值如下:
(24)
(25)
从而得到原方程的孤子解:
(26)
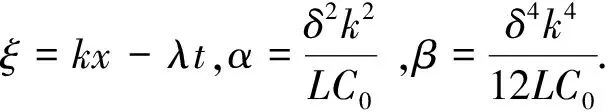
1.4 情形4
设(1)的孤子解为:
u(ξ)=ptanh4(qξ).
(27)
将(27)式代入变分公式(4)中,得到双参数p、q的函数:
(28)
讨论(28)的稳定性,建立联立方程组:
(29)
(30)
然后,求解上述方程组,得到参数p、q的取值如下:
(31)
(32)
从而得到原方程的孤子解:
(33)

2 结语
He-变分方法是求解偏微分方程精确解的有效工具,本文基于He-半逆解法,对弱色散解非线性波动方程进行构造对应变分公式,进而寻找这些方程的孤子解.这些结果显示,该变分方法简单明了,利用它可以构造其他学者用行波法、影射法和Sine-Cosine方法等法所求得解之外的孤立子解.同时,由此方法得到非线性传输线的波动方程具有孤立波解,这是一个很重要的结论,如果把电压波的振幅认定很小,还可以把方程(1)化为KDV方程.
参考文献:
[1] 欧朝芳, 胡颉, 佘守宪.非线性传输线中的孤子[J].大学物理, 2006, 25(2): 42-45.
[2] 岳萍,龚伦训. 弱色散非线性波动方程的孤波解和Jacobi椭圆函数解[J].大学物理,2008,27(12):15-17.
[3] 郭鹏, 陈宗广, 孙小伟.非线性传输线方程的几类显式精确解[J].大学物理,2010,29(4):20-21.
[4] 郭鹏,陈宗广,孙小伟.求解非线性传输线方程的简便方法[J].大学物理,2012,31(9):25-26.
[5] HE J H.Some asymptotic methods for strongly nonlinear wave equation [J].Internet J Modern Phys B, 2006 ,20 (10):1141-1199.
[6] HE J H.Non-preservative methods for strongly nonlinear problems [J].Berlin: dissertation.De-Verlag in Internet GmbH, 2006.
[7] HE J H.New interpretation of homotopy perturbation method[J].Internet J Modern Phys B, 2006 ,20(18):2561-2568.
[8] Erdunbuhe, Temuerchaolu.A Generalized (G'/G)-expansion method and its applications to the Whitham-Broer-Kaup-like equations [J].内蒙古师范大学学报:自然科学汉文版, 2012,41(2): 120-131.
[9] TAO Z L.Variational approach to the Benjamin Ono equation [J].Nonlinear analysis: real world applications, 2009,10(3):1939-1941.
[10] TAO Z L.Solving breaking solution equation by He′s variational method [J].Comput Math Appl, 2009 (58):2395-2397.
[11] ZHANG J.Variational approach to solitary wave solution of the generalized Zakharov equation [J].Comput Math Appl, 2007 (54):1043-1046.

