基于贝叶斯方法的流量数据的不确定性分析*

顾西辉，张 强

(中山大学 水资源与环境系∥华南地区水循环与水安全广东省普通高校重点实验室，广东 广州 510275)

水文资料整编规范(2000)指出[1]：水位流量关系受到冲淤、变动回水、洪水涨落、水生植物、结冰等因素的影响，会产生不确定性。国内外对于这种不确定性的分析进行了大量研究。程伟等[2]对三峡水库蓄水后下游近坝段水位流量关系中的研究指出：河道侵蚀基点条件是影响水位流量关系的主要因素; 戴凌全等[3]用多次幂多项式函数作为水位流量关系的拟合公式，用最小二乘法进行拟合；夏军强等[4]提出一维水动力模型对黄河下游平摊流量进行分析; 董晓华等[5]基于最小二乘法对绳套型水位流量关系曲线进行拟合。此外采用改进的BP神经网络、混合禁忌搜索算法、简化的人工鱼群算法等算法进行水位流量关系曲线的拟合[6-8]。文献[9]对意大利Po河流域下游河段进行上述各个来源不确定性定量分析，得出流量总的不确定性在6.2%～42.8%之间；José-Luis Guerrero等[10]用广义似然估计和蒙特卡洛方法分析水位流量关系的时间变异性。上述研究对于水位流量关系的时空变异和流量数据的不确定性大小及原因有着重要的科学意义。

但是以往的研究往往局限于对水位流量关系曲线的拟合方法、拟合线型的研究，并且在流量不确定性方面局限于冲淤、变动回水、洪水涨落、水生植物、结冰等因素对拟合精度的影响，对水位流量关系的变异性引起的不确定性研究较少，而水位流量关系变异是多种因素影响下的结果，同时也是流域水资源管理等诸多实践应用的基础。基于此，本次采用贝叶斯方法来估计水位流量幂律关系式的参数，定量界定水位流量关系变异性引起的平均低流量、平均中流量和平均高流量的不确定性[11]。东江流域是珠江流域主要支流之一，主要担负珠三角地区大城市，如广州、东莞等，以及香港80%的用水，对于保障区域水资源安全与社会稳定具有极其重要的作用和意义。研究东江流域流量不确定性对于东江流域水资源管理具有重要理论与现实意义。

1 研究区域和数据

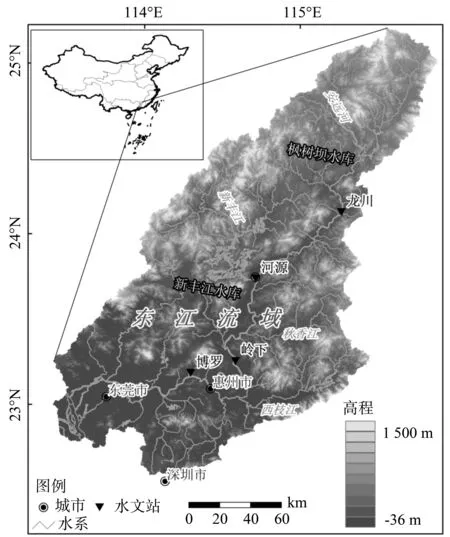
图1 河源、岭下和博罗3个测站的地理分布图Fig.1 The geographic distribution of three stationsHeyuan，Lingxia and Boluo

东江属于珠江三大水系之一，位于中国南方湿润地区，长度523 km，流域总面积35 636 km2，平均坡降为0.35‰。本文以东江流域河源、岭下和博罗3个测站为研究对象(图1)。采用河源站1981-2009年水位流量数据，岭下站1956-2009年水位流量数据，博罗站1956-2005年水位流量数据进行研究。

2 研究方法

2.1 水位流量曲线拟合的贝叶斯公式

本文采用有着位置参数的幂律关系式，进行单一曲线法推流[1]:

(1)

公式中，Q是流量，h是水位。(A1,A2,…,An)是尺度参数，(b1,b2,…,bn)是形状参数，h0是位置参数，代表河道横断面最低点的高程，(h1,h2,…,hn-1)是不同片段水位流量曲线的分割点，例如：河道的深槽、边滩、低滩、高滩等由于水力性质、径流条件等因素的差异，公式(1)中的各种参数是不同的。由于各个片段在拟合时是相互独立的，所以本文只考虑一条单一的水位流量曲线进行研究。文献[12]以假设河道横断面宽度-深度呈指数关系作为基础，结合曼宁公式推导上述满足幂律关系的水位流量关系式，给出了公式(1)详细的水力学方程式推导过程。单一片段的对数回归模型为：

qi=a+blg(hi-h0)+εi

(2)

公式(2)中qi=lg(Qi)，a=lg(A)，为尺度参数A的自然对数值。εi为模型残差，假设εi～N(0,σ2)。构造向量θ=(a,b,h0)，根据贝叶斯概率公式，参数(θ,σ2)的后验概率密度函数为：

f(θ,σ2|D)=

(3)

公式(3)中，D代表实测的水位-流量值，L是似然函数，π是先验分布。

2.2 流量不确定性计算公式

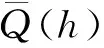
(4)

3 分析结果

3.1 贝叶斯方法的拟合优度检验

参数a和b分别是河道的尺度参数和形状参数，共同为河道水力性质和横断面几何形状所决定，所以给予一个二维联合正态分布作为先验分布。位置参数h0给予一个无信息先验分布，噪声(公式(2)对数回归模型残差)参数σ2给予一个逆伽马分布。作者在另一篇文章详细介绍了参数集(a,b,h0,σ2)的先验分布、后验分布以及推断方法。

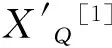
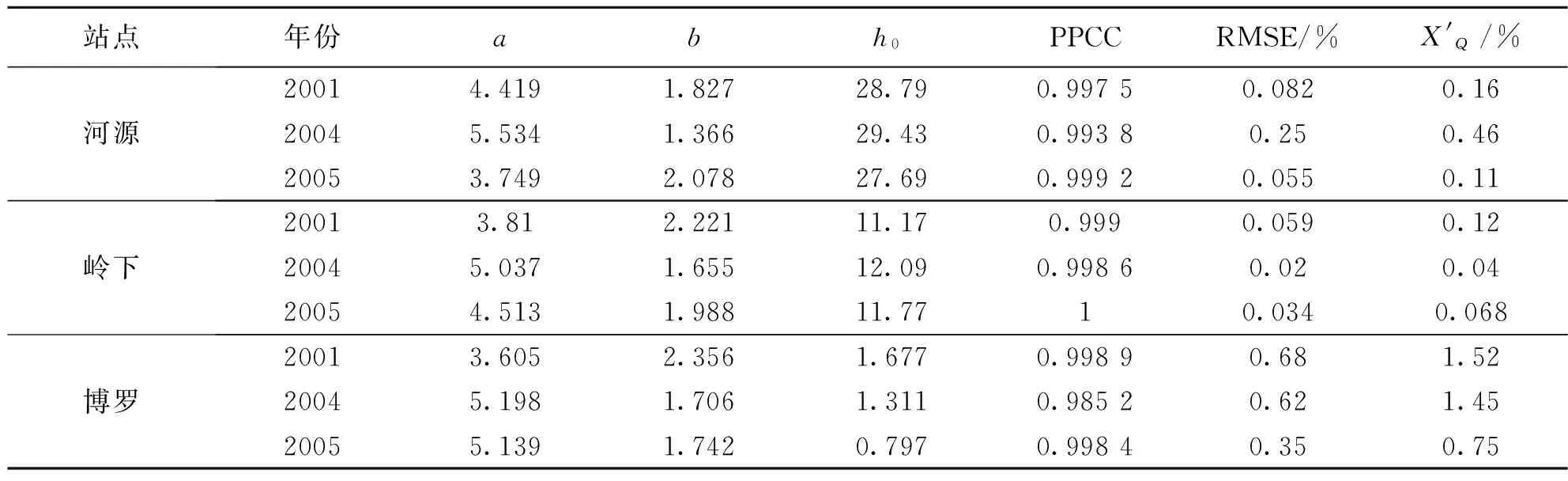
表1 贝叶斯方法拟合的参数值和拟合优度指标

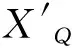
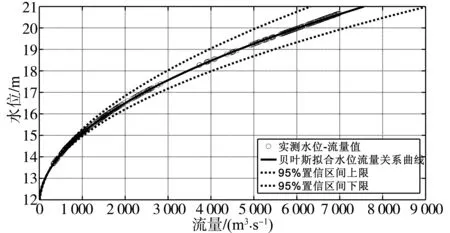
图2 岭下站2005年水位流量关系的贝叶斯拟合效果及置信区间Fig.2 The fitting effect and confidence interval of stage-discharge relationship fitted by Bayesian method in Lingxia station

3.2 水位流量关系的时间变异性

公式(2)中的尺度参数a、形状参数b和位置参数h0反映出了河道水力特性和横断面几何形状的变化情况。用贝叶斯方法分别分析1981-2009年河源站, 1956-2009年岭下站和1956-2005年博罗站逐年的水位-流量数据，研究尺度参数a、形状参数b和位置参数h0的变化情况(图3，表2)。

从图3中可以看出，以1980年为分界点，岭下站的尺度参数a呈下降趋势，形状参数b呈上升趋势，博罗站正好相反。河源站在1980年之后，变化情况规律性不明显，总体来说，尺度参数a和形状参数b均呈下降趋势。对于位置参数h0，3个测站均呈下降趋势，这种趋势在1980年之后表现的更加显著。并且博罗站在3个测站中的下降趋势最显著。这些变化可能受到1980年代东江流域开始兴起的大量采砂的影响。Luo等[14]指出：从1986-2003年珠江流域共采掘沙子超过8.7×108m3，其中导致东江流域河道平均下切1.77～6.48 m。河道采沙的另一后果是导致河道形状向窄深方向发展，即河道宽深比下降[15]。参数h0持续下降反应了东江流域河床下切的现象，参数a、b反映了河道形状—宽深比的变化。

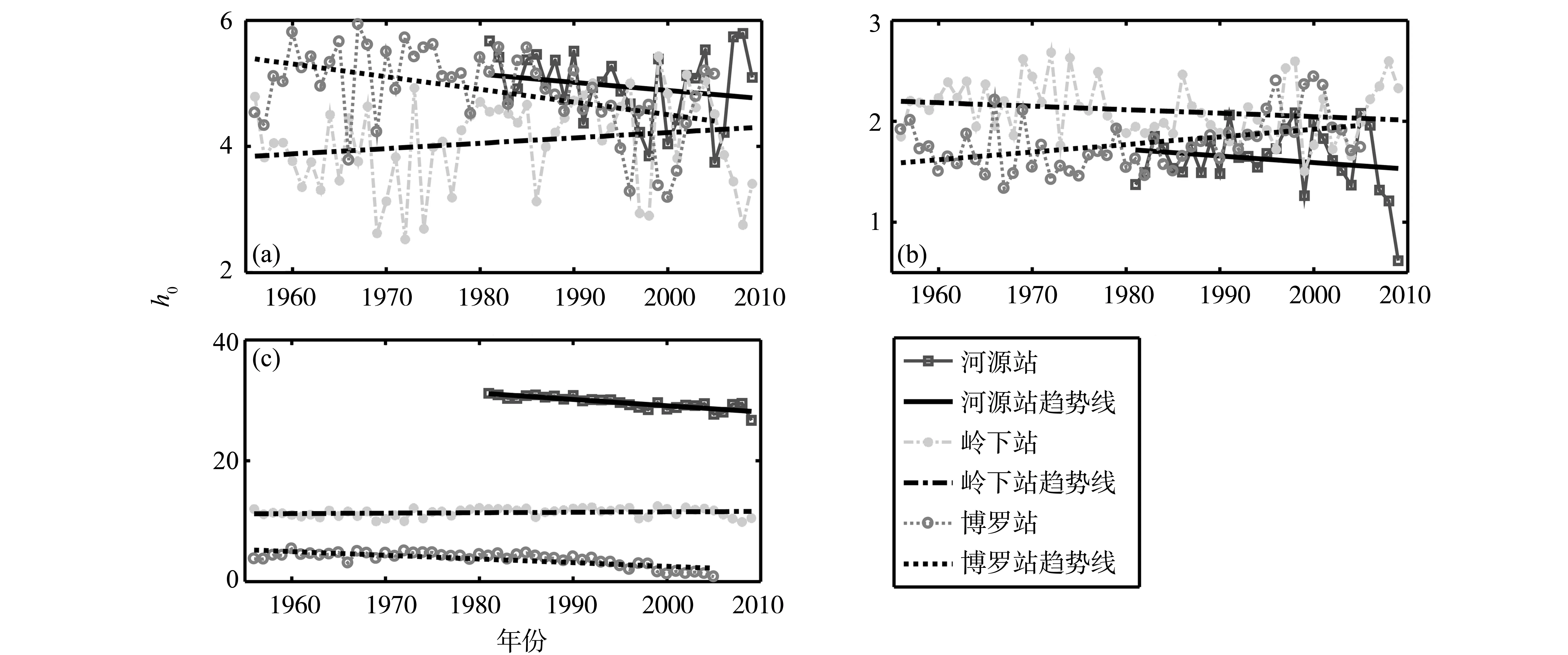
图3 河源站、岭下站和博罗站贝叶斯估计的系数历年变化及趋势图Fig.3 The coefficients changing with time estimated by Bayesian method and their trends of Heyuan，Lingxia and Boluo stations

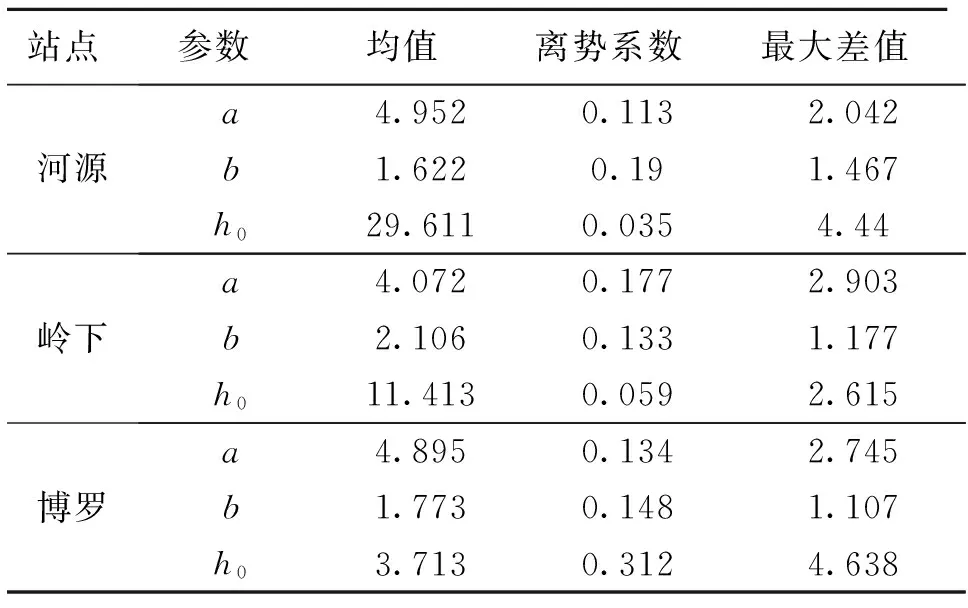
站点参数均值离势系数最大差值河源a4.9520.1132.042b1.6220.191.467h029.6110.0354.44岭下a4.0720.1772.903b2.1060.1331.177h011.4130.0592.615博罗a4.8950.1342.745b1.7730.1481.107h03.7130.3124.638

从河源、岭下和博罗站各个参数变化情况来看，洪水对尺度参数a和形状参数b的趋势也起到了显著的影响。比如1959年的洪水，岭下站尺度参数a由下降趋势变成上升趋势，同样的情况也出现在1966年洪水。1994、2005年2场洪水则把尺度参数a由上升趋势变成下降趋势。所以洪水对河道水力特性以及几何形状的影响比较复杂，变化没有明显统一的趋势。

从表2中可以看得出来，地理位置相对靠近河口的岭下站和博罗站比相对远离河口的河源站，其离势系数相对较大，这表明东江流域河道水力特性和几何形状的变化越靠近河口，变化越剧烈，其水位流量关系的不确定性也应该相应的增加。这种性质也可以从参数的最大差值中进一步的反映出来。

3.3 水位流量关系的变异性引起的不确定性

东江流域河源、岭下、博罗3个测站每一年的水位数据作为一个时间序列。使用这个时间序列的水位值，用贝叶斯推断的水位流量关系曲线来估计流量值，同时计算相关的95%置信区间的上界和下界。公式(4)用近似的求和公式来代替，求取平均的低流量、中流量和高流量的不确定性(图4)。图4中可以看出3个测站1956-1974年，低流量、中流量和高流量的不确定性总体趋势均在减小。珠江流域20世纪60-70年代大规模的联围筑闸、整治河道使河道形状趋于稳定，同时河道内流量趋于稳定，这一时期水位流量关系受到干扰较小，相对稳定。90年代末期，低流量、中流量和高流量不确定性总体趋势趋于稳定(2009年除外，2009年珠江流域遇到大旱，流量的急剧减小是不确定性升高的主要原因)；河源站、岭下站和博罗站，低流量、中流量和高流量的不确定性趋于吻合，个别年份有较大差异。主要因为90年代末期东江流域主要水利工程已经修建完毕、河道大量采沙得到有效管理和治理，河道形状趋于稳定，并且东江流域3大水库(枫树坝、新丰江、白盆珠)对东江流域径流量的有效调节，综合影响下，东江流域低流量、中流量和高流量流量大小差距显著变小，水位流量关系趋于稳定。

70年代中期，岭下站低流量不确定性有一个明显增加的跳跃性变化。这一时期枫树坝和新丰江两座水库的建成和运行使得岭下站河道枯水期流量增加，低流量水位流量关系产生明显异变。70年代中期到90年代初，岭下站低、中、高流量普遍高于其他时期(图5(b))。这一时期河道采沙大量增加，对河道形状变化影响剧烈，水位流量关系非常不稳定。

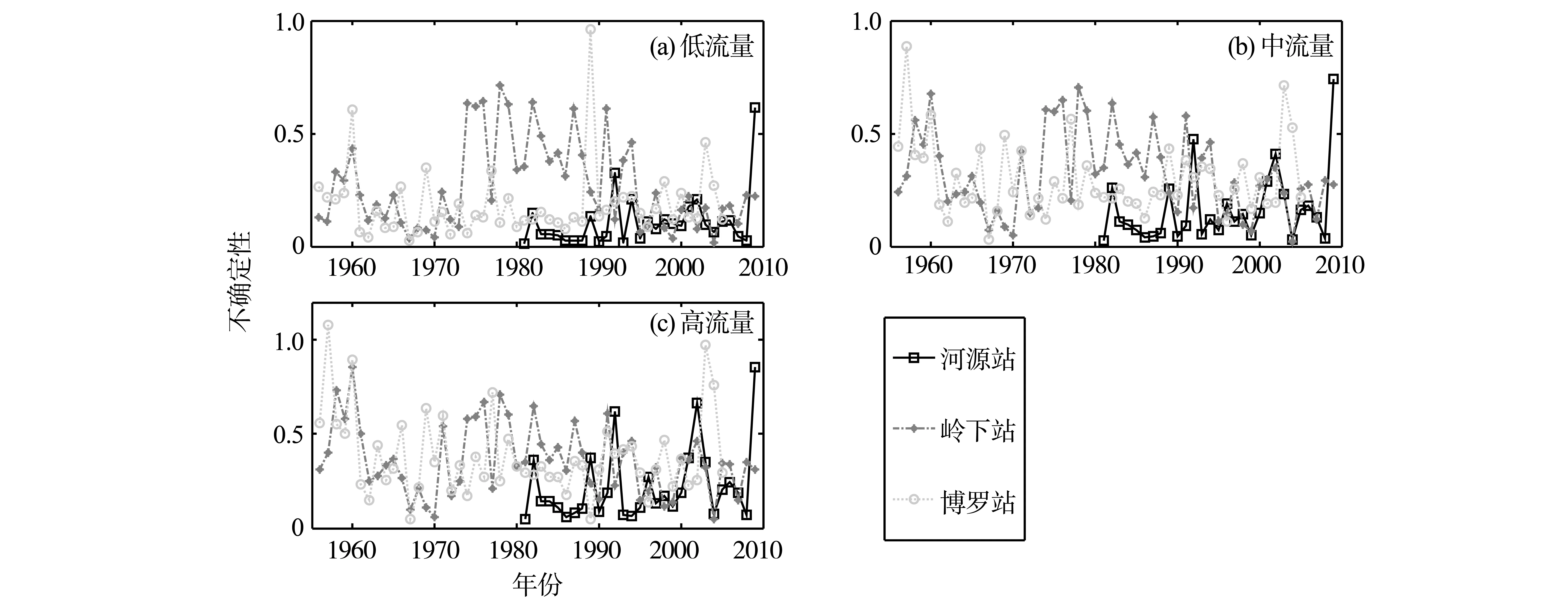
图4 河源站、岭下站和博罗站低流量、中流量和高流量不确定性Fig.4 The uncertainty in low flow、medium flow and high flow of Heyuan、Lingxia and Boluo stations

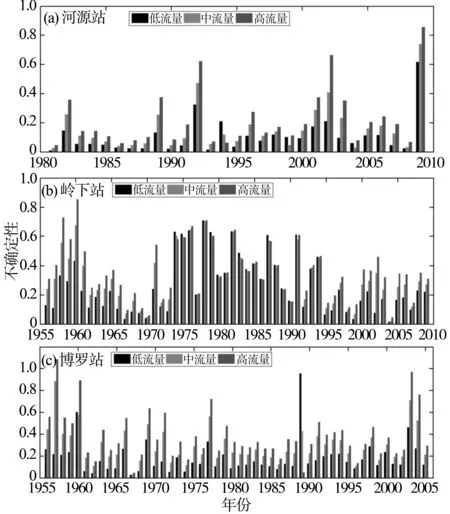
图5 河源、岭下和博罗3站历年流量不确定性Fig.5 The flow uncertainty over the years of Heyuan,Lingxia and Boluo stations

单个测站来说，河源站、岭下站和博罗站，表现的共同规律是：高流量不确定性最大，中流量不确定性次之，低流量不确定性最小(个别年份除外)。以博罗站为例(图5c)，绝大部分年份，高流量要比中流量、低流量的不确定性要大，最高达到108%。由于博罗站位于东江流域的干流，上有秋香江等支流的汇流，因此水量充沛，洪峰流量曾经达到12 800 m3/s(1959年)。高流量条件下，洪水对河道的冲刷、河道断面几何形状以及河道水力特性的改变更加剧烈，相比低、中流量，高流量还涉及到河漫滩的形状、水力性质以及粗糙度的变化。基于上述原因，高流量不确定性相对较大。但是，图5(c))显示，70年代初期之后，高流量和低、中流量不确定性的差异显著在减小。1974年新丰江水库和枫树坝水库的建成和使用，对博罗站的消峰作用很明显，有效的调节了博罗站高、低流量之间的差距。两大水库对稳定博罗站流量的不确定性起到了很大作用。

河源站、岭下站和博罗站每一年的水位-流量数据作为一个时间序列，共有133个时间序列。文献[11]提出了一个质量等级系统：不确定性在0～9%，10%～19%，20%～39%，40%～79%和>80%被分别评为优、良、中、差和极差。统计这133个时间序列不确定性在各个等级中的比例(图6)。可以看出，东江流域低流量不确定性集中在0～20%，占到63%，表现最好。这一点与文献[11]在挪威测站的研究是不同的：他认为挪威测站低流量不确定性表现最差。而东江流域高流量不确定性相对较大，集中在20%～40%，属于中等水平。中流量不确定性居于低、高流量之间，不确定性低于40%的比例达到78%。总体来说，东江流域流量不确定性在中等偏上水平。

从均值和离势系数来看(表3)，三个测站共同表现的规律是：流量越大，其不确定性的均值越大，离势系数越小；同一类别的流量，越靠近河口，不确定性的均值相对较大，离势系数相对较小。

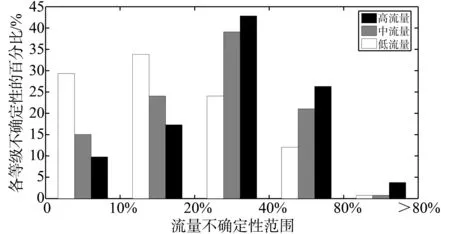
图6 133个时间序列流量不确定性各等级统计比例Fig.6 The statistical proportions of each grade of 133 time series flow uncertainty

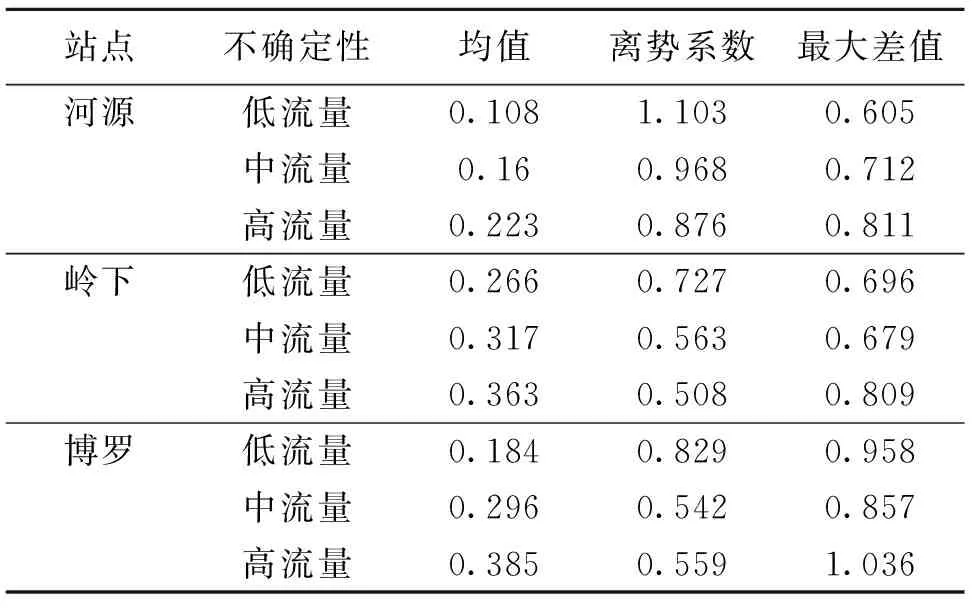
表3 河源站、岭下站和博罗站不确定性统计值Table 3 The statistical values of uncertainty in Heyuan，Lingxia and Boluo stations

这说明：同一个测站，低流量的不确定性相对较小，变化幅度相对较大；同一类别流量，越靠近河口，流量的不确定性相对较大，变化幅度相对较小。

4 结 论

本文通过用贝叶斯方法推断水位流量幂律关系式的参数，继而求出水位流量关系的变异性引起的不确定性，得出以下结论：

2)东江流域水位流量关系时间变异性显著，河源站和博罗站河道尺度参数呈下降趋势，形状参数呈上升趋势，岭下站则相反。3个测站的位置参数均呈下降趋势。3个测站参数的变化趋势以1980年为分界点，前后变化显著。

3)东江流域20世纪60-70年代大规模的联围筑闸、整治河道对减小3个测站的流量不确定性有显著的作用；20世纪70年代中期到90年代初期，大规模的河道采沙对岭下站流量不确定性影响最显著。90年代之后，河源站和岭下站流量不确定性在稳定减少，博罗站流量不确定性呈增加趋势；3个测站低、中、高流量不确定性之间的差距减小。

4)东江流域高流量不确定性相对较大，集中在20%～40%，属于中等水平。中流量不确定性居于低、高流量之间，不确定性低于40%的比例达到78%。总体来说，东江流域流量不确定性在中等偏上水平。

[1] 水利部长江水利委员会水文局.水文资料整编规范[S],2000.

[2] 程伟,陈立,许文盛,等. 三峡水库蓄水后下游近坝段水位流量关系[J].武汉大学学报：工学版,2011,44(4):434-444.

[3] 戴凌全,戴会超,蒋定国,等. 基于最小二乘法的河流水位流量关系曲线推算[J].人民黄河,2010,32(9):37-39.

[4] 夏军强,吴保生,李文文. 黄河下游平滩流量不同确定方法的比较[J].泥沙研究,2009(3):20-29.

[5] 董晓华, 薄会娟, 邓霞. 基于最小二乘法的绳套型水位流量关系最优定线研究[J].中国农村水利水电,2010(1):51-55.

[6] 李中志. 基于改进 BP 神经网络的水位流量关系拟合[J].中国农村水利水电,2008(10):30-35.

[7] 汪嘉杨,李祚泳,倪长健,等. 基于混合禁忌搜索算法的水位流量关系拟合[J].系统工程,2006,24(6):107-110.

[8] 施秋红, 王联国. 基于简化的人工鱼群算法的水位流量关系拟合[J].甘肃农业大学学报,2010,45(2):147-151.

[9] BALDASSARRE G D, MONTANARI A. Uncertainty in river discharge observations: a quantitative analysis[J].Hydrology and Earth System Sciences Discussions, 2009(6):39-61.

[10] GUERRERO J L, WESTERBERG I K, HALLDIN S， et al. Temporal variability in stage-discharge relationships[J].Journal of Hydrology, 2012, 446-447: 90-102.

[11] PETERSEN-ØVERLEIR A, SOOT A, REITAN T. Bayesian rating curve inference as a streamflow data quality assessment tool[J].Water Resour Manage, 2009, 23(9):1835-1842.

[12] REITAN T, PETERSEN-ØVERLEIR A. Dynamic rating curve assessment in unstable rivers using Ornstein-Uhlenbeck processes[J].Water Resources Research, 2011, 47(2):1-14.

[13] 曹深西，陈子燊.广东沿海的极值风速概率分布研究[J].海洋通报，2013,32(1):12-18.

[14] LUO X L, ZENG E Y, JI R Y, et al. Effects of in-channel sand excavation on the hydrology of the Pearl River Delta, China[J].Journal of Hydrology, 2007, 343(3/4):230-239.

[15] 季荣耀，陆永军，左利钦. 东江下游博罗河段人类活动影响下的河床演变[J].泥沙研究, 2010(5):48-54.