自发辐射诱导原子质心运动退相干的理论研究*

姜文英，赵志敏，刘玉洁，张文举， 郑 丽，郑泰玉

(1.南京航空航天大学自动化学院，江苏南京 210016；2.桂林电子科技大学电子工程与自动化学院，广西桂林 541004；3.大连工业大学信息科学与工程学院，辽宁大连 116034；4.大连工业大学生物工程学院，辽宁大连 116034；5.东北师范大学物理学院，吉林长春 130024)

经典力学适用于宏观物体，而量子力学适用于微观物体。但是，量子力学作为物理学的基本规律，也应该适用于宏观物体，它应以经典力学的规律作为其极限情况。量子力学中的一维谐振子是一个很好的例子。在低激发态，粒子的位置几率分布和经典几率分布差别极大，而当量子数变得相当大时，量子力学分布逐渐接近经典分布。这是Bohr对应原理的体现。另外，量子力学认为任何物体都具有波粒二象性，宏观物体也不例外，虽然日常所观测的现象并没有发现宏观物体具有量子相干性，但是人们已经 从实验上观测到了宏观物体的量子相干效应。这说明了量子力学与经典物理并不相矛盾，它们对世界的描述有些差异，却是相容的。

对于是什么机制使得宏观物体的量子相干性丧失的研究，不仅可以帮助人们更好的理解量子世界与经典世界的过渡，而且对量子信息学的发展也有着重要意义[1-3]。人们曾经尝试从各种角度去回答这个问题，也经历了各种各样的争论，但最终发现量子退相干理论能对这一问题给出正确的解释。关于量子退相干的机制，人们曾提出了许多模型理论[4-9]。人们也进行了许多相关的实验研究来演示量子退相干的动力学过程[10-12]，量子相干性的消失和恢复。几十年来，退相干的机制始终是集中研究和争论的课题，物理学家用模型演示这种机制，逐渐取得共识的是退相干的根源是环境的影响。目前人们研究了各种各样环境诱导退相干的模型理论[13-14]，试图在量子力学的框架中理解量子退相干问题。

本文根据环境诱导退相干的理论，研究了单个二能级原子与真空电磁场的相互作用，结果表明，原子的自发辐射会诱导原子的质心运动的空间量子相干性消失，从而导致原子间相对位置空间局域化。

1 系统的薛定谔方程及精确解

考虑二能级原子的激发态和基态分别为|e〉和|g〉。原子跃迁频率是w0，原子质量是m0，它的空间位置用x表示，相应的动量为p。若原子放置在一个真空的电磁场中，则原子内部状态将与电场耦合，在旋转波近似下，二能级原子与场相互作用的哈密顿量为

(1)

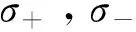
我们考虑系统处在一维空间中。设t=0时刻，系统的初始波函数可写为|Φ(0)〉=|ψ(0)〉⊗|e〉⊗|0〉。即原子的内部电子态处于激发态，电磁场处于真空状态，|是原子的空间自由度的初始态，在原子的动量表象中，它可以写为动量算符的本征态|p〉的叠加：

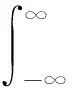
(2)

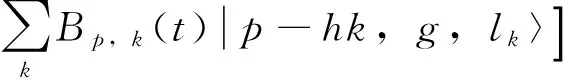
(3)

系数Ap(t)和Bp,k(t)是和时间相关的量，通过求解薛定谔方程，我们得到(通过用Weisskopf-Wigner近似):

(4)

定义

A0=Cp，

hωA=p2/(2m)+hω0，

hωB=(p-hk)2/(2m)-hω0/2+hωk，

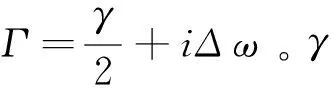
2 约化密度矩阵

ρ(x,x′,t)=ψ(x,t)ψ*(x′,t)F(x,x′,t)

(5)

在此计算过程中，把ψ(x+hk,t)在x附近展开到了一级近似，并假定ω0≫Γ。

(5)式中，F(x,x′,t)是退相干因子，其定义为

(6)

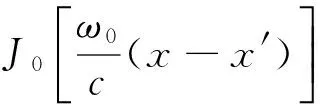
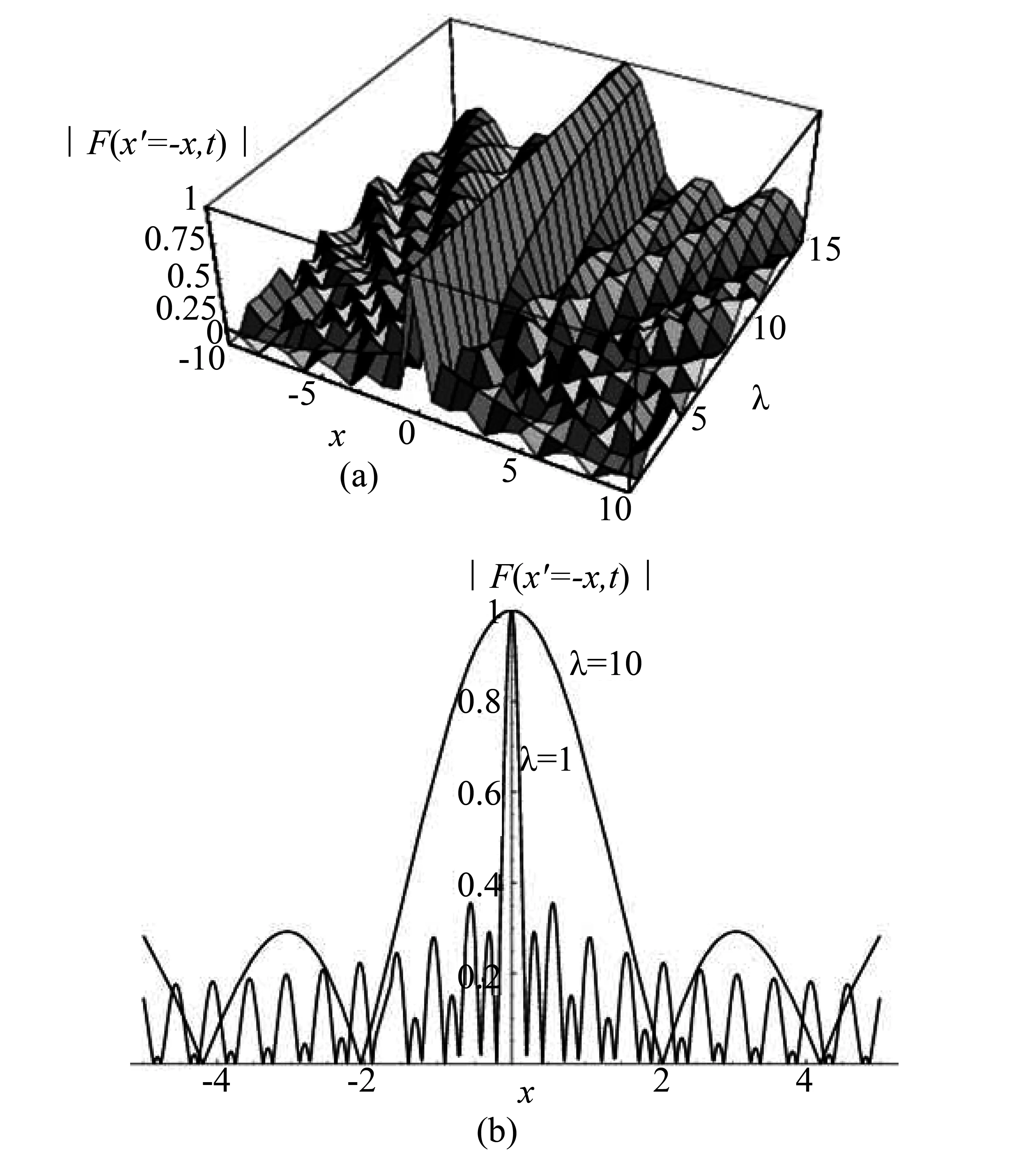
图1 退相干因子|F(x′=-x,t)|示意图Fig.1 Schematics of decoherence factor |F(x′=-x,t)|(a)|F(x′=-x,t)|随x和λ的变化而不同，(b)某一相同时刻不同辐射光子波长下|F(x′=-x,t)|随x变化的示意图

另外，我们分析退相干因子F(x′=-x,t)跟原子位置以及耦合常数间的关系。图2中，给出了三种不同位置情况下，退相干因子随时间的演化情况，可以看出，退相干与原子的位置或原子尺度相对原子辐射光子的波长大小有密切关系，在某情况下，原子的空间运动会发生完全退相干，即退相干因子会在有限时间内完全变为零，而某些情况下，原子的空间运动只会发生部分退相干。这些参数可以帮助寻找原子的退相干自由子空间。图3给出了更清楚地三维图像，即退相干因子F(x′=-x,t)随时间和位置的变化图像。图3给出的是不同耦合强度下，退相干因子F(x′=-x,t)随时间和原子位置的演化图示。图中从图3(a)至图3(d)，耦合常数g逐渐变大，可以看出，耦合常数越小，原子空间退相干时间越长，即原子与场的耦合越弱，原子空间运动的相干性越好，原子内态与场耦合越强，原子的空间位置退相干就会越明显。

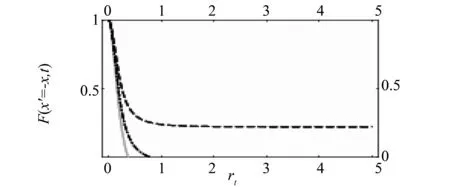
图2 退相干因子|F(x′=-x,t)|在不同原子尺度情况下随时间演化示意图Fig.2 Evolution of |F(x′=-x,t)| for different x图中虚线对应x=0.5λ，点虚线对应x=1.42λ，实线对应x=0.8λ

3 原子质心运动的空间量子退相干

假设(2)式中的原子质心运动的初始态波函数|ψ(0〉是两个在中心位置分别在a与-a的高斯波包的叠加，则在x表象中，其表达式为

(7)

(8)

图3 退相干因子F(x′=-x,t)随时间和位置演化的图示。Fig.3 Demonstration for the evolution of F(x′=-x,t) with time and the atomic position(a)g=0.1; (b)g=0.5; (c)g=2; (d)g=5

图4给出了约化密度矩阵ρ(x,x′,t)随时间演化的示意图(分别对应两种不同情况下的三种不同时间)，一种情况是无自发辐射时的演化，另一种存在自发发射时的演化情况。我们可以看到在有自发发射的情况下，首先波包的扩散被抑制，其次两波包的空间相干性随着时间而衰减。当t≫tD时，沿着x=-x′方向的两个波峰可以在有限的时间内衰减到几乎为零，并且不会复原。因此原子质心运动的相干性被明显破坏。显然由于原子的自发辐射，使得原子的空间自由度与真垦电磁场间产生量子纠缠，从而所导致的原子的空间自由度发生退相干。

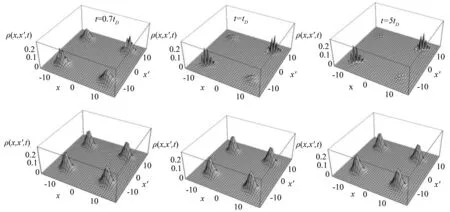
图4 原子质心运动的约化密度矩阵随时间的演化示意图Fig.4 Schematics of the reduced density matrix for the motion of the atomic center of mass(第一排图像为有自发辐射时的情况；第二排为自由演化时的情况)

5 总 结

本文主要分析了原子的内部自由度对其质心运动的空间量子相干性的影响，通过考虑原子内部电子态与真空电磁场的耦合，讨论了原子质心运动的退相干动力学。在weisskopf-wigner近似下，通过求解薛定谔方程，给出了总哈密顿量的解析解和描述原子质心运动的约化密度矩阵。在此基础上，进一步讨论了其量子退相干动力学演化情况。我们发现，原子的自发辐射诱发了原子的空间自由度态、原子的电子态与真空电磁场间的量子纠缠，从而破坏了原子质心运动的量子相干性。

[1] 惠萍, 黄纲明.CdSe量子点系统的库仑相互作用能的量子尺寸效应[J].中山大学学报:自然科学版，2004，43(4):38-40.

[2] 林位株, 寿倩, 刘鲁宁,等.AlGaAs/GaAs多量子阱中相干控制光电流的超快弛豫[J].中山大学学报:自然科学版，2004，43(6):73-76.

[3] 文家焱; 梁世东.基于绝热量子演化的量子状态转换方法[J].中山大学学报:自然科学版，2007，46(4):22-25.

[4] ZEH H D. On the interpretation of measurement in quantum theory[J].Found Phys, 1970，1(1):69 -76.

[5] ZUREK W H. Pointer basis of quantum apparatus: Into what mixture does the wave packet collapse[J].Phys Rev D，1981, 24(6):1516-1525.

[6] ZUREK W H. Environment-induced superselection rules[J].Phys Rev D，1982，26(8):1862-1880.

[7] BOSE S, JACOBS K, KNIGHT K L.Scheme to probe the decoherence of a macroscopic object[J]. Phys Rev A，1999，59(5):3204-3210.

[8] SUN C P, LIU X F, ZHOU D L，et al. Localization of a macroscopic object induced by the factorization of internal adiabatic motion[J].Eur Phys J D，2001，17(10):85-92.

[9] ZHANG P, LIU X F,SUN C P. Consistent approach for quantum measurement[J].Phys Rev A，2002，66(4):042104.

[10] BRUNE M, HAGLEY E, DREYER J, et al. Observing the progressive decoherence of the “Meter” in a quantum measurement [J].Phys Rev Lett，1996，77(24):4887-4890.

[11] MYATT C J, KING B, TURCHETTE Q A,et al. Decoherence of quantum superpositions through coupling to engineered reservoirs[J].Nature，2000，403(1):269-273.

[12] FRIEDMAN J R, PATEL V, CHEN W,et al.，Quantum superposition of distinct macroscopic states[J]. Nature，2000，406(6):43 -46.

[13] ZHENG L,LI C, LI Y, et al. Localization of the relative position of two atoms induced by spontaneous emission[J].Phys Rev A,2005，71(6):062101.

[14] ZHENG L, YANG C P, NORI F. Quantum dynamics of spatial decoherence of two atoms in a ring cavity[J].Phys Rev A, 2010，82(6):062106.