双连续C半群的Vornonvskaja型逼近问题*

仓定帮，闫守峰，苗文静

(华北科技学院基础部，北京 101601)

当今，强连续半群的理论已经成为许多领域的重要工具。这些领域除了传统的偏微分方程和随机过程外，还包括量子力学、无穷维控制理论、积分-微分方程、泛函微分方程及无穷维动力系统等等[1]。

然而在实际问题中发现，许多情况下对应的半群不是强连续的，Kuhnemund[2]指出，存在Banach空间上的一些特殊的非强连续的半群，并通过对这些半群的具体研究；Kuhnemund在Banach空间上附加一个比范数拓扑粗的局部拓扑，使得半群在局部拓扑下强连续，从而提出了双连续半群的概念。文[2]还指出序列完备的局部凸空间上的等度连续半群满足的条件比双连续半群强，且等度连续对实际的问题对实际的问题的应用不是很广，许多情况所对应的空间是Banach空间，可以赋予一个比范数拓扑粗的局部拓扑，从而说明双连续半群理论有非常好的应用价值。文[3]给出了双连续半群的Trotter-Kato定理，文[4]分析了局部凸拓扑下的Riemann-Stieltjes积分，给出了双连续半群的逼近定理及其应用。文[5]研究了局部有界的双连续C半群，结合双连续半群和C半群的逼近定理，得到了双连续C半群的逼近定理。逼近理论是半群的重要的研究分支，20世纪80年代开始，数学家们开始利用概率论这一有力工具解决算子半群中的逼近问题，并取得了丰富的成果[6-11]。本文借助于双正则核这一工具，试从不同的角度研究了双连续C半群的表示形式，给出了双连续C半群Vornonvskaja型逼近定理。

1 若干定义

假设X是Banach空间，X′是它的共轭空间，τ是X上的一个局部凸拓扑，并且具有以下的性质：

(i)空间(X,τ)是在‖g‖-有界集上序列完备，即每个‖g‖-有界的τ柯西列在(X,τ)中收敛；

(ii)τ拓扑比‖g‖拓扑粗且τ是Hausdorff拓扑；

(iii)(X,‖g‖)中的范数可以由空间(X,τ)′定义，即对每个x∈X有‖x‖=sup{|φ∈(X,τ)′,‖φ‖(X,‖g‖)′≤1}。

记Φ={φ∈(X,τ)′,‖φ‖(X,‖g‖)′≤1}，Pτ是上的局部凸拓扑所对应的半范数蔟，由假设不失一般性，不妨认为p(x)≤‖x‖，x∈X，p∈Pτ。本文中的所有算子均为线性算子，D(A)表示算子的定义域。

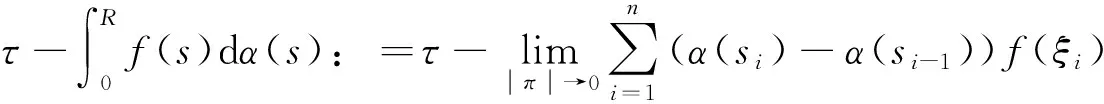
都成立，其中ξi∈(si-1,si)，|π|=max(|si-si-1|)。

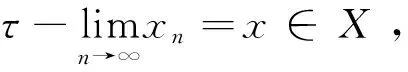
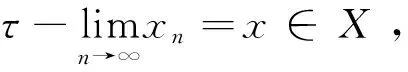
定义4[2]算子族{T(t)}t≥0⊆B(X)称为局部等度双连续，若对每个t0≥0，子集{T(t):0≤t≤t0}等度双连续。

定义5[2]算子族{T(t)}t≥0⊆B(X)称为指数有界的双连续C半群，简称为双连续C半群，如果满足

(i)T(0)=C，T(t+s)C=T(t)T(s),∀t,s≥0；

(ii){T(t)}t≥0强τ-连续；

(iii){T(t)}t≥0局部等度连续；

(iv){T(t)}t≥0指数有界，即∃M,ω≥0使得‖T(t)‖≤Meωt，∀t≥0。

线性算子A称为双连续C半群{T(t)}t≥0的生成元，如果

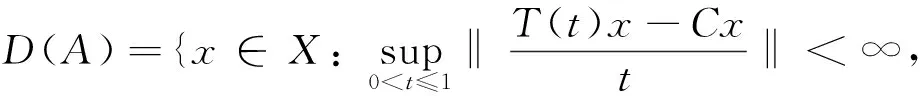
A的预解集为ρ(A)={λ:λ-A为单射λ,lm(C)⊆lm(λ-A)}，A的预解式为

由双连续C半群的定义可以发现S(kt)=[C-1S(t)k]C。

定义6 设φ(t)>0，若Wη(t,μ)满足下面条件(a)、(b)时，称Wη(t,μ)为双正则核。

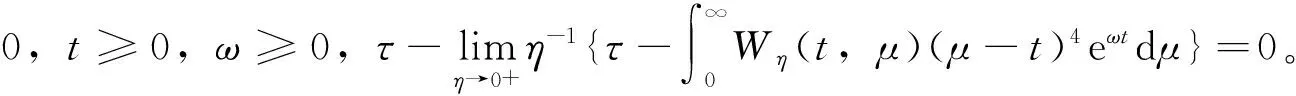
2 主要结论

证明∀x∈X,t≥0，

由于{S(t)}t≥0是双连续的，所以∀ε>0,∃δ>0,当|μ-t|<δ，有p[S(t)x-S(t)x]<ε，因此

p[Sη(t)x-S(t)x]≤

p[Sη(t)x-S(t)x]≤

结合定义6可得p[Sη(t)x-S(t)x]≤ε+(ε+Meωt)o(η)+M(1+eωt)o(η)，得证。

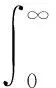
进一步，我们假设Wη(t,μ)还满足下面的两个条件：

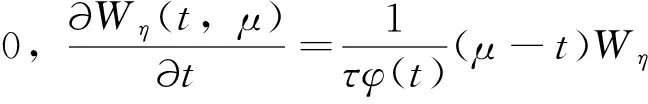
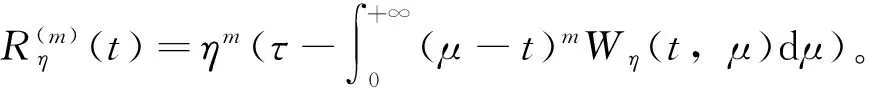
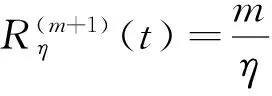
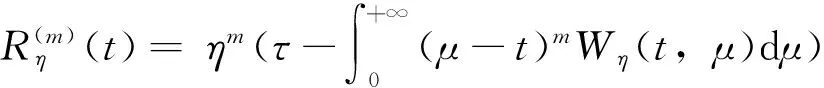
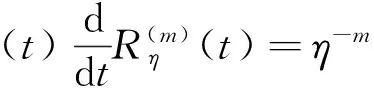
m(μ-t)m-1Wη(t,μ)]dμ)=

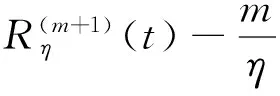
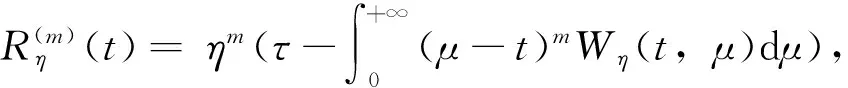
证明∀t≥0,η>0,由Schwarz不等式得

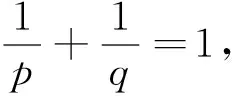
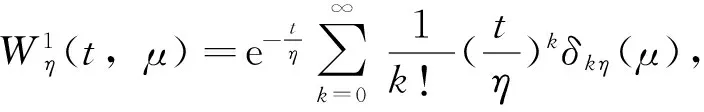
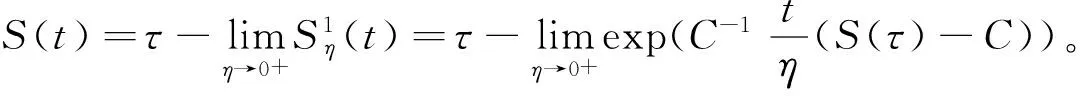
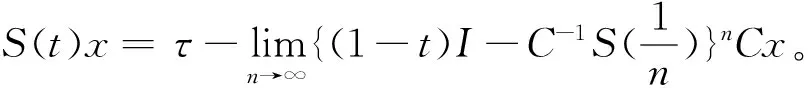
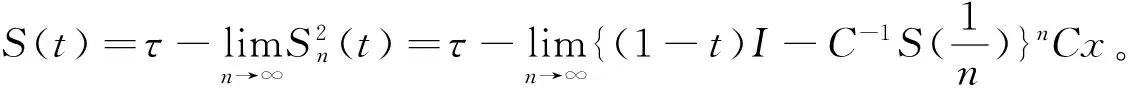
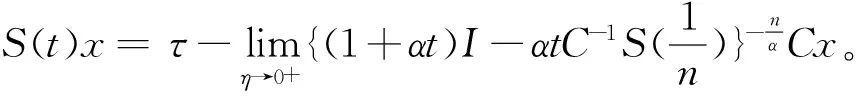
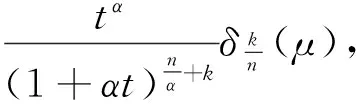
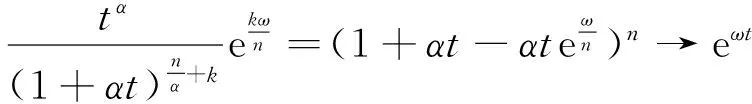
在上面的定理4中令α→0+可得如下推论1。

证明令L(λ)=(λ-A)-1C，则(λ-A)L(λ)=C，对该式微分k次得

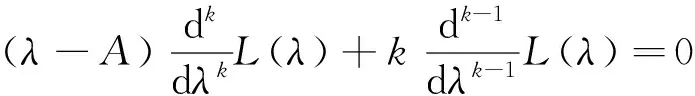
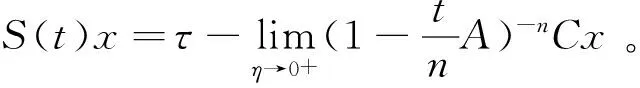
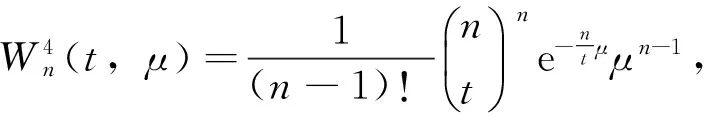
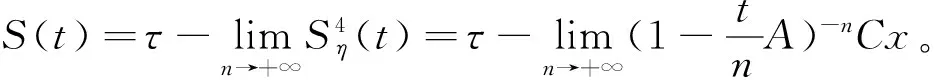
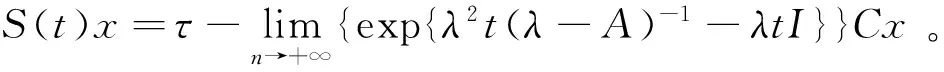
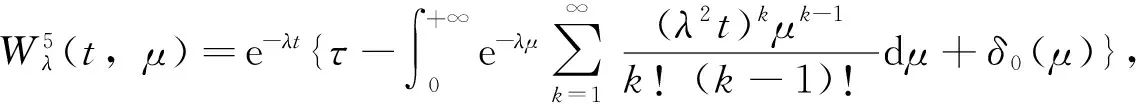
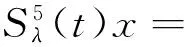
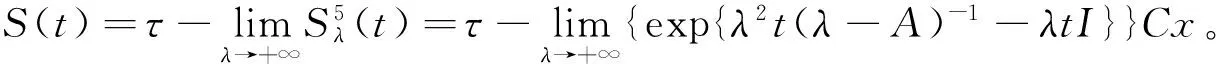
下面给出双连续C半群的Vornonvskaja型逼近定理。

定理7 设{S(t)}t≥0是指数有界的双连续C半群，Wη(t,μ)满足条件(c)和(d)，若x∈D(A2S(t0))则有:

[S(μ)x-S(t)x)]dμ)=I1+I2

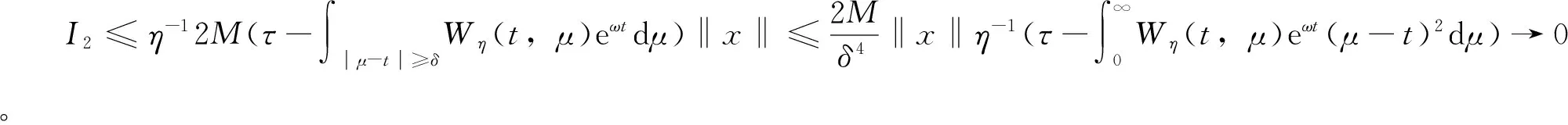
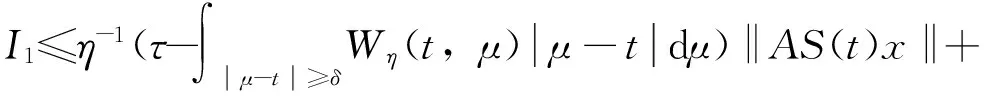
因而当η→0+,ε→0+时有I1=o(1)。结合定理2、4、7可得如下推论2。

推论2 设{S(t)}t≥0是指数有界的双连续C半群，若x∈D(A2S(t0))则

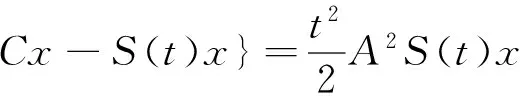
[1] 黄永忠.算子半群及应用[M]. 武汉：华中理工大学出版社，2011.

[2] KUHNEMUND F. A hille-yosida theorem for bi-continuous semigroups [J]. Semigroup Forum, 2003, 67(2):205- 225.

[3] ALBANESE A A, MANGINO E. Trotter-Kato theorems for bi-continuous semigroups and applications to Feller semigroups [J]. J Math Anal Appl, 2004, 289(2): 477-492.

[4] JARA P. Rational approximation schemes for bi-continuous semigroups [J]. Journal of Mathematical Analysis and Applications, 2008, 344(2): 956-968.

[5] 王文娟,孙国正.局部有界的双连续C-半群及其逼近定理[J]. 数学杂志，2007, 27(1): 31-37.

[6] PFEIFER D. Approximation-theoretic aspects of probabilistic representations for operator semigroups [J].Journal of Approximation Theory, 1985, 43(3): 271-296.

[7] PFEIFER D. Probabilistic concepts of approximation theory in connection with operation semigroups [J].Approximation theory and its Applications, 1985, 1(4): 93-118.

[8] PFEIFER D, BURTER P L. Some general probabilistic estimations for the rate of convergence in operator semigroup representions [J]. Applicable Analysis, 1986, 23: 111-118.

[9] 陈文忠. C-无穷小生成元的表示式[J]. 厦门大学学报：自然科学版,1993, 32(2): 135-140.

[10] 陈文忠. C半群概率表示的饱和定理[J]. 厦门大学学报：自然科学版,1995, 34(1): 1-6.

[11] 宋晓秋，彭爱民，王彩霞. C半群与积分半群的概率型逼近问题[J]. 南京大学学报：数学半年刊, 2003, 20(2): 216-225.