热连轧精轧宽度控制技术的研究及应用

李家波，李维刚 ，张健民，郭朝晖

(1.宝钢集团中央研究院，上海，201900；2.东北大学信息科学与工程学院，辽宁 沈阳，110819)

当前市场上对热轧带钢尺寸精度的要求日益提高,其中带钢厚度和板形的精度已基本满足需求，而宽度精度还有进一步提升的空间。在带钢全长方向上，宽度偏差越大，需要切除的宽度余量也就越大。宽度余量每减小1 mm，成材率大约提高0.1%，可显著提高经济效益[1]。因此各热轧厂都在努力提高带钢宽度精度，以减少切边量。

目前粗轧的宽度控制技术已比较完善，带钢的宽度问题主要集中在精轧区域。精轧出口的带钢宽度控制主要包含两个方面：①带钢头部防拉窄；②带钢中部的宽度余量控制。针对头部拉窄问题，主要从轧机穿带速度设定和活套起套控制等方面进行改进，但仍未能有效避免拉窄现象。带钢中部的宽度余量控制与粗轧和精轧的设定及控制都有关系。粗轧的设定主要包括宽展预测模型、狗骨宽展模型等，粗轧的控制主要是基于立辊的自动宽度控制；精轧的设定主要包括宽展预测模型和张力预设定模型，精轧的控制包括宽度前馈控制、宽度反馈控制以及活套多变量控制[2]。精轧宽展预测模型由于受到精轧各种因素的影响，很难预测准确；精轧宽度前馈控制需要额外增加测宽仪，并且很难准确跟踪；宽度反馈控制存在大时滞的影响等，这些因素造成目前精轧区域的宽度控制精度难以进一步提高。

针对以上不足，本文提出一种新的精轧带钢宽度控制综合解决方案。在带钢头部，开发精轧机架速降补偿自学习模型，为活套创造良好的起套条件，避免带钢头部拉窄现象；在带钢中部，引入力矩因子，减少全长宽度波动；增加精轧宽度反馈控制和宽展预测模型修正功能，以提高带钢全长宽度精度。

1 精轧区域宽度控制研究现状

在热连轧精轧控制过程中，穿带是一个十分重要而又难以控制的环节，从咬钢开始到活套控制稳定投入之间的一段时间内，很容易出现张力剧烈波动，造成带钢头部拉窄。为避免这种现象，贾大朋等[3]提出了基于活套初始高度预测模型的活套“软接触”定位控制，但这种方法仅考虑了冲击速降对活套初始高度的影响，未考虑过程机设定的前后不匹配性，并且只是被动地进行穿带活套控制，难以适应各种干扰的影响。Park等[4]提出通过咬钢后相邻两机架间电流的增量偏差计算带钢头部张力，进行调速控制。该功能只是在咬钢后500 ms内起作用，受轧机调节速率的限制，很难进行快速调整，对防止带钢头部拉窄作用不大，并且通过机架电流计算张力存在较大的偏差。根据现场实际生产经验来看，带钢头部拉窄一般出现在后机架咬钢1 s以后。所以就现有公开的技术来看，带钢头部拉窄问题还未能很好地解决。

针对带钢中部宽度波动问题，米田裕紀等[5]介绍了测宽仪前馈型自动宽度控制，该功能需要在机架间安装测宽仪，然后通过跟踪带钢偏差，在后续机架间进行张力调节。使用该方法要增加设备成本，并且机架间环境恶劣，很难保证测宽仪的正常工作。王爱丽等[6]提出轧制力前馈型自动宽度控制方法，根据F1机架轧制力的变化预测带钢硬度的变化，进而通过模型计算带钢宽度的偏差，然后调整后续机架间的张力。由于轧制过程中影响轧制力的因素很多，很难将它们区分开来。

在精轧机架出口处均安装有测宽仪FDW，为提高精轧带钢全长的宽度精度，许多生产线都设有宽度反馈控制功能。王丽君等[7]提出了精轧宽度反馈自抗扰控制算法；彭开香等[8]提出了基于RBF网络的直接广义预测精轧宽度控制方法。这些方法还处于理论层面，离实际应用还有一定距离，并且单个活套控制能力有限，较难达到控制目标值。

2 精轧带钢宽度控制技术研究

2.1 精轧带钢头部防拉窄控制

为解决带钢头部拉窄问题，首先要了解穿带过程中活套套量产生的两个主要原因：①过程机在设定前后机架Fi和Fi+1的初始辊缝和轧机速度时，机架间的流量不匹配；②咬钢时机架冲击速降与冲击补偿的合成。第一个原因比较容易理解，假设其在机架间形成的套量为ΔL1(其值可正可负)。第二个原因导致的套量形成过程如图1所示，带钢咬入下游机架Fi+1之前，在穿带速度的基础上额外添加一个冲击补偿值Nd，Fi+1咬钢时，Nd撤销，机架产生一个自然速降，这个过程是机架间减小的套量ΔL2(ΔL2<0)的形成过程。同时，Fi+1机架轧机在冲击力矩的作用下，产生一个动态速降Δnd，且这个动态速降的恢复需要一定的时间，这个过程是增加的套量ΔL3(ΔL3>0)的形成过程。若ΔL1、ΔL2、ΔL3三者之和小于0，则很容易造成带钢头部拉窄；若三者之和大于0，则在前后机架之间便形成了一定的活套起套套量，这个值越大，活套初始起套角就越大，严重时会造成活套起套后控制角度的剧烈波动，甚至是机架间堆钢，活套角度剧烈波动则会带来张力的剧烈波动，从而造成带钢头部拉窄。

图1 下游机架咬钢的速降过程Fig.1 Process of speed drop at the downstream stand

为给活套创造良好的起套条件，防止带钢头部拉窄，本文采用各机架冲击速降补偿值Nd自动调整的方法。其基本原理是通过对起套过程中活套角度的综合评估，确定实际角度与理想角度的偏差，将该角度偏差通过模型计算转换成冲击补偿速度偏差的大小，将该速度偏差按照“钢种×厚度×宽度×机架”进行规格分类自适应学习。具体实施步骤如下。

步骤1在数据表中按照“钢种×厚度×宽度×机架”设置初始冲击补偿值Nd，并从基础自动化系统中以20 ms的间隔采集活套闭环控制投入后1 s内活套实际角度θact(i)、活套对主传动的速度调节量ΔvLP(i)。

步骤2根据采集到的数据，计算活套实际起套角度θLP，计算过程如下。

(1)

n值视实际情况而定，要能够反映活套的初始调节情况。

θLP=max{θact(i)}

(2)

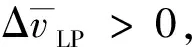
(3)

m值视实际情况而定，要能够反映一段时间内活套的实际角度。

步骤3根据实际起套角度θLP和目标角度θaim分别计算实际起套套量Lact和目标套量Laim，其具体计算过程可参照文献[9]，最后得到套量偏差为：

ΔL=Lact-Laim

(4)

步骤4根据套量偏差计算理想冲击补偿修正值ΔNd，如图2所示，Δt为自然速降经历的时间，其形成的套量可以近似为一个三角形，则：

(5)

步骤5利用理想冲击补偿修正值ΔNd对初始冲击补偿值Nd进行修正，见式(6)，得到新的冲击补偿值Nd-new，将其保存到数据库内，用于下一块相同规格钢的轧制。

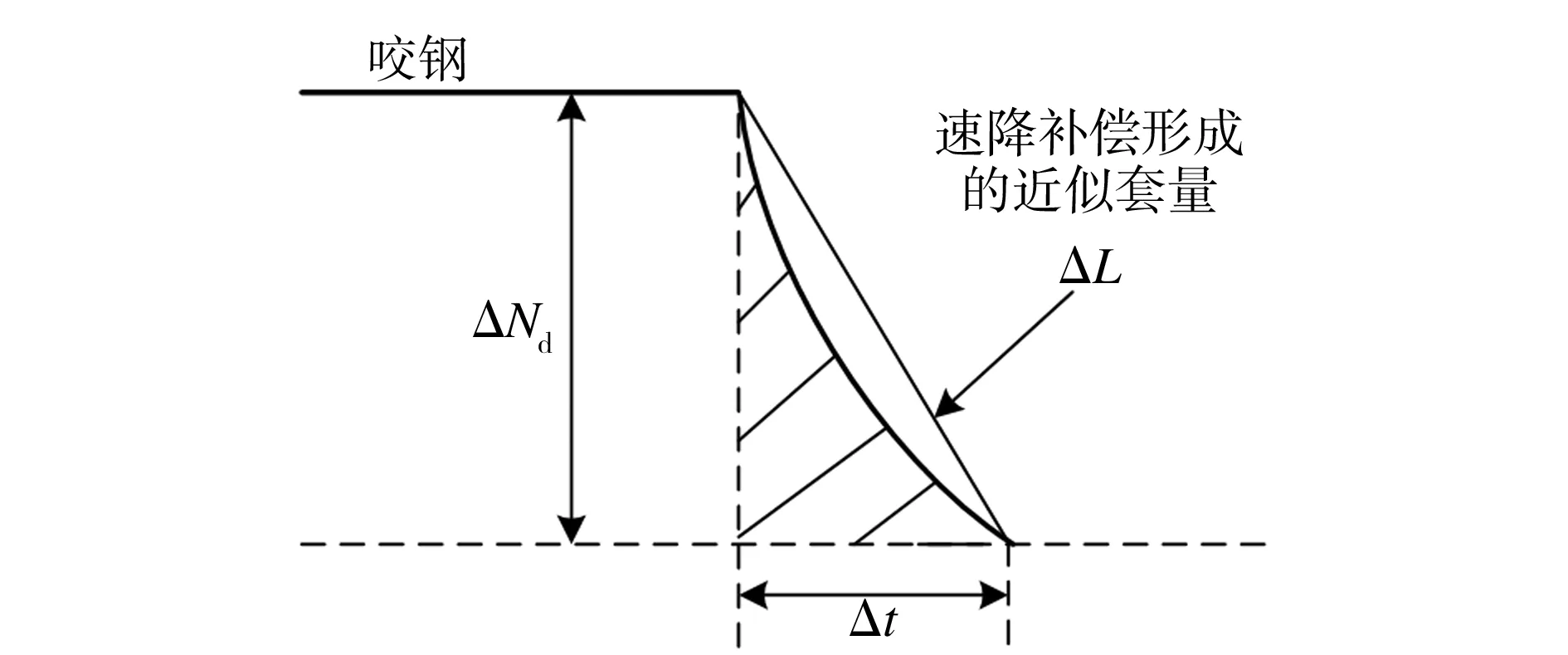
图2 冲击速降补偿形成的套量Fig.2 Loop produced by speed drop compensation

(6)

式中：γ为模型学习系数，短时系数取0.2，用于本批次同规格带钢的学习；长时系数取0.1，在本批次带钢轧制时学习，学习结果用于下一批次同规格的带钢轧制。

采用上述方法不仅可以补偿由于冲击速降造成的机架间的流量偏差，而且还可以补偿过程机初始设定的流量偏差。这是由于对于同批次相同规格的带钢来说，各机架的过程机初始设定和轧机状态差别不大，通过冲击速降补偿值的自动学习调整，基本可以使初始流量偏差稳定在一定范围内。而对于不同批次同规格的带钢来说，变化较大的仅为轧机状态，上一批次的学习值仍有较高的使用价值。

2.2 精轧带钢中部宽度控制

2.2.1 带钢中部宽度波动控制

带钢中部较大的宽度波动主要由水印点带来的较大温度波动所引起。当温度波动点经过前后机架时，会引起机架间套量和张力的变化，进而影响带钢宽度。本文在活套力矩控制中，针对张力矩部分，引入张力稳定因子KCT,此时张力矩计算公式如下。

(7)

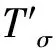
正常轧制时，活套在设定角度附近工作。当温度高点经过前后机架时，活套角度上升，减小张力矩，防止带钢拉窄；当温度低点经过前后机架时，活套角度下降，增加张力矩，调节带钢多余的宽度。同时，活套角度上升时，减小张力矩可以抑制活套角度的上升趋势；活套角度下降时，增大张力矩可以抑制活套角度的下降趋势，从而保持机架间活套角度的稳定。在实际调试时，一般前面几个活套取值较小，后面几个活套取值较大。该方法可以较好地解决由于来料温度波动引起的精轧带钢宽度波动问题。

2.2.2 带钢宽度反馈控制(FAWC)

由于在精轧设备配置上，精轧出口的测宽仪离最近的活套辊的距离也有9 m左右，即带钢到达测宽仪的最短时间大概为0.5 s，采用这个测量值进行宽度反馈控制属于一个大时滞的控制系统。因而对于一些较高频率的宽度波动，通过该控制方式是无法消除的，并且它们的存在会影响整个反馈控制系统的稳定性，需要对其进行滤波处理，滤波常数的取值范围为0.5～10 s。在已解决带钢中部较高频率宽度波动的基础上，针对变化缓慢、持续时间较长的宽度偏差，在精轧6个活套进行分配后，进行PI反馈控制，调节各个活套的张力设定值，控制结构如图3所示。对每个活套来说，需要调节的宽度偏差如下式所示。

(8)

式中：ΔWi为活套LPi调节的宽度偏差；ΔW为实测的宽度偏差值；ti为滤波时间常数；K1i为宽度偏差在每个活套上的分配增益，取值范围为0～1，一般情况下，活套位置从后向前时，该值逐渐减小。

图3 精轧宽度反馈控制结构示意Fig.3 Structure of strip width feedback control

2.2.3 精轧宽展预测模型修正

一般情况下，过程机在对精轧的宽展量进行预测和利用精轧出口测宽仪测得的宽度偏差进行学习时，未考虑FAWC的影响。当精轧出口本条带钢初始宽度偏差较大时，FAWC功能就可能将各活套的设定张力调至上限或者下限，而过程机的宽度偏差学习功能无法考虑到这部分已被调节的宽度偏差。这样就有可能会使活套系统在轧制下条带钢时经常处于大张力或者小张力的控制状态，影响精轧系统的稳定性。

为消除这种影响，需要将FAWC投入后各个活套的实际张力设定值σi，连同各活套上游机架带钢出口速度Vi、精轧出口实测带钢温度TFDT等多项数据动态发送给过程机，通过下述过程，计算得到本条带钢轧制时FAWC功能已调节的宽度偏差。

步骤1以精轧出口实测带钢温度TFDT为基础，根据过程机对各个机架的温度分配系数KTi，实时计算各机架出口的带钢温度Ti如下：

Ti=TFDTKTi

(9)

(10)

(11)

f(Wi,hi,Ti,σi,ti,i+1)=Wiγ(Wi/hi)·

[exp(-0.5εi/100)-1]

(12)

(13)

ti,i+1=L/[(1+fi)Vi]

(14)

步骤3计算在整个轧制过程中，6个活套相对于各自的设定张力对带钢总的拉窄量：

(15)

步骤4过程机根据上述计算的拉窄量，在对后续同批次的带钢进行粗轧区域目标宽度设定时，可进行如下修正：

(16)

3 应用效果

本文提出的精轧带钢头部防拉窄控制功能在宝钢集团某热轧产线三电改造工程中得以实施，保证了活套起套的稳定性，带钢头部拉窄现象降低了30%左右。图4为增加带钢头部防拉窄控制后，前后两块钢的精轧出口实测宽度偏差数据。从图4中可以看出，采用冲击速降自学习调整后，后一块钢的头部拉窄量得到明显改善。

图4 防拉窄控制后相邻两块钢的宽度偏差

Fig.4Stripwidthdeviationbetweenfrontandrearstripswithanti-shrinkagecontrol

通过精轧带钢中部的宽度反馈控制以及过程机学习功能，有效提高了精轧出口的带钢宽度精度。图5所示为同种规格的带钢分别在系统改造前后轧制时精轧出口的带钢宽度数据。从图5中可以看出，系统改造后带钢宽度偏差大幅减小。从带钢全长数据来看，系统改造前带钢宽度偏差离9 mm的目标值相差较远，而改造后的带钢宽度偏差基本接近于目标值。

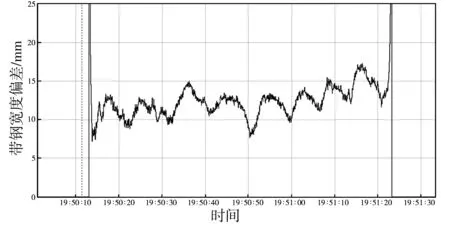
(a)改造前

(b)改造后

图5系统改造前后的带钢宽度偏差

Fig.5Stripwidthdeviationbeforeandaftersystemreform

4 结论

(1)本文提出的精轧冲击速降自学习模型，可有效弥补过程机设定模型的偏差，提高穿带过程活套控制的稳定性，减少带钢头部拉窄现象。

(2)通过在精轧各个活套合理配置张力稳定因子，提高了活套系统的稳定性，同时减少了带钢宽度波动现象。

(3)开发的精轧宽度反馈控制和宽展预测模型修正功能，在保证活套系统稳定性的基础上，提高了带钢全长的宽度精度。

[1] 吕程，王国栋、刘相华，等.热连轧精轧宽度自动控制[J].钢铁研究，1997，98(5)：52-56.

[2] Park C J, Lee D M, Choi S G. Development of fuzzy PID control system for hot strip finishing mill[C]//The 27th Annual Conference of the IEEE Industrial Electronics Society. Denver, USA, 2001:287-791.

[3] 贾大朋，张殿华，丁桦，等.热连轧过程中活套辊与带钢“软接触”定位控制[J].轧钢，2005，22(2)：45-47.

[4] Park C J, Hwang I C. New tension control at the head of strip in hot strip finishing mill[J]. Journal of Materials Processing Technology, 2008, 206：69-77.

[5] 米田裕紀,潮海弘資，岡田誠康，等.熱間仕上ミルにおける高精度幅制御技术の開発[J]. CAMO-ISIJ, 1996,9：312-315.

[6] 王爱丽，刘华强，杨荃，等. 基于张力调节的热连轧精轧机组宽度控制的研究[J]. 钢铁，2010，45(3)：62-65.

[7] 王丽君，童朝南，孙一康.自抗扰控制在监控精轧宽度控制系统中的应用[J]. 系统仿真学报，2006,18(6)：1615-1622.

[8] 彭开香，徐品.基于RBF网络直接广义预测精轧宽度控制[J]. 控制工程，2009, 16(6)：727-730.

[9] 李家波，张健民，杜江舰，等.宝钢1580 mm热轧三电改造活套控制技术[C]//第五届宝钢学术年会论文集.上海，2013：105-109.