基于迷宫算法思想的梯形图向AOV图的转换

王吉停，张得礼，周来水

(南京航空航天大学机电学院，江苏 南京，210016)

软PLC的编程语言遵循IEC61131—3标准，该标准定义了5种PLC编程语言，其中梯形图沿袭了传统控制图的表达方式，具有直观明了、易于掌握等特点[1]，但其对于PLC来说是不可执行代码，无法直接运行，而指令表是一种用于嵌入式平台且能直接转化为二进制代码的汇编语言，因此，在PLC软件开发过程中，实现梯形图向指令表程序的转换有利于软件的整合和解读，通过对指令表的编译或解释执行便可实现PLC程序的逻辑控制。目前关于梯形图向指令表转换的研究中，大多都用到了中间数据结构AOV图[2-7]。AOV图能很好地反映梯形图各元件之间的连接关系，与梯形图有良好的对应关系，相比直接将梯形图转化为指令表的方法来说，AOV图能提高转化效率。

梯形图向AOV图转换算法的难点在于梯形图中各元件直接前驱和直接后继元件的确定。文献[3]和文献[6]中是通过元件坐标来判断当前顶点的直接前驱和直接后继顶点，最终实现向AOV图转换的，但该方法不适合处理串并联关系复杂的程序，而且可扩展性不好。文献[4]中提到基于迷宫算法思想的梯形图向AOV图转换的算法，但没有具体阐述。本文利用迷宫算法思想来确定梯形图各元件的直接前驱和直接后继元件，并给出了具体的实现方法。

1 AOV图数据结构

用顶点表示活动, 用弧〈i,j〉表示活动i必须在活动j开始之前完成。这种有向图叫作用顶点表示活动的AOV 图。对〈i,j〉弧而言,i是j的直接前驱,j是i的直接后继。采用十字链表[8]存储结构对AOV图进行存储，易于计算顶点的出度和入度。

一个梯形图程序是由多个梯级网络组成的，每个梯级网络又由各种图符构成，包括功能单元图符、连接单元图符以及空单元。各个梯级网络内的梯形图本质上对应着一个有向图, 其中各功能单元图符可以抽象为有向图中的顶点, 连接单元图符可以抽象为有向图中的弧。

为简化转换算法，将梯形图中的图符元件对应的AOV图顶点分为以下4种类型：

(1)源顶点SNode。将左侧起始线作为一类特殊的元件保存在相应的对象中，作为AOV图的起始标志，存储在Xlist[0]中，其入度为0，出度大小由程序需要决定。

(2)尾顶点TNode。将右侧终止线也作为一类特殊的元件保存在相应的对象中，作为AOV图的结束标志，存储在顶点数组的最后位置处，出度为0，入度大小由程序结构决定。

(3)竖直元件顶点VNode。竖直线连接元件作为各行之间连接关系的标志，本程序将具有直接连接关系并且列值相等、行值最小的竖直线元件作为一类顶点VNode，其出度和入度均不小于1。

(4)功能元件(水平线元件除外)作为另一类顶点FNode，其入度和出度均为1。

2 梯形图向AOV图转换算法描述

梯形图向AOV图转换分为3个阶段。第一阶段：确定AOV图的所有顶点。对当前梯形图按从左向右、从上向下的顺序进行扫描，得到所有的顶点，并存储在顶点数组Xlist中。在扫描过程中，竖直连接线元件也作为AOV图顶点存储在顶点数组中，这样可以避免文献[6]中提到的“虚顶点”问题；水平连接元件不作任何处理。第二阶段：AOV图各顶点的直接前驱和直接后继顶点的扫描。本阶段的实现最为关键也最为复杂，本文利用迷宫算法思想[8]来实现各顶点直接前驱和直接后继顶点的扫描，在扫描过程中只扫描当前顶点的直接后继顶点，扫描到直接后继顶点的同时，将当前顶点作为其直接后继顶点的直接前驱顶点存储，这样省去了直接前驱顶点的扫描过程，避免了重复扫描，使算法复杂度降低。第三阶段：AOV图十字链表存储结构的创建。通过第一、第二阶段的处理，已经提取出AOV图的所有顶点及各顶点的直接前驱和直接后继连接关系信息，作一个for 循环, 遍历各个顶点, 并定位顶点data后继链表中存储的元素，即得到它们在图中的顶点编号，然后建立相应的弧， 当后继链表中指向空时, 就完成了该顶点弧的建立,再作下一个循环, 直至所有顶点都遍历完毕，这时图就建立起来了。

3 转换算法的实现

在转换算法执行前，定义了以下处理算法：

(1)元件直接前驱后继信息的存储算法Rule_Save(A，B)：将B加入A的直接后继链表中，A加入B的直接前驱链表中。

(2)直接后继顶点为竖直线顶点的处理算法Rule_Vline：直接后继顶点为竖直线顶点时，元件右连接属性向上或向下连接标志为真，得到当前位置处的竖直线，从而得到与该竖直线有直接连接关系并且列值相等、行值最小的竖直线C，返回C；若没有竖直线与当前竖直线相连，则返回当前位置处的竖直线。

(3)水平线处理算法Rule_Hline：判断当前水平线的右连接属性，如果只有向右连接属性，则继续向右搜索，直至扫描到功能元件(FNode)或具有其他连接属性的水平线为止。若为功能元件F，则将功能元件F返回；若为具有其他连接属性的水平线，则通过调用算法Rule_Vline得到元件C，返回C。

(4)水平向右处理算法Rule_Right：得到与当前元件A同一行的右边相邻的元件B。若B为功能元件(FNode)，返回B； 若B为水平线，则通过调用水平线处理算法Rule_Hline，得到当前元件A的直接后继元件B，再返回B。

转换算法的流程图如图1所示。首先，顺序遍历顶点数组Xlist得到一个顶点，并判断顶点的类型，然后根据顶点的类型进行相应的扫描处理，直至遍历完顶点数组中的所有顶点为止，具体步骤如下：

步骤1：顺序遍历顶点数组Xlist得到一个顶点A，若A不存在，则转换算法结束；若A存在，则转步骤2执行。

步骤2：判断当前顶点A的类型，利用迷宫算法思想对A进行扫描处理，得到A的直接后继顶点。不同类型顶点的处理规则如下：

(1)若当前顶点A为功能元件顶点FNode，由前可知，A的出度和入度均为1，可以判断A的直接前驱和直接后继顶点均只有1个，则每当确定了A的一个直接后继顶点后，就停止对A的扫描处理，转向步骤1。

算法中涉及到的功能元件顶点所有可能的右连接属性如图2所示。其扫描过程如下：

图2 功能元件的右连接属性Fig.2 Right connection properties of functional elements

图1 转换算法流程图

① 根据当前顶点A的右连接属性(向上→向下→向右)，找到所有可能的搜索方向，将搜索路径存入向量S中，搜索路径包括顶点名称和搜索方向。

② 顺序遍历向量S中的所有路径，若搜索路径存在，则沿搜索路径进行搜索，否则转步骤③。搜索是一个匹配的过程，即PLC的假想“电流”在该路径的方向上要能流通。根据搜索方向的不同，分以下两种情况：(a)如果当前的搜索方向向上或向下，则停止对当前顶点A的扫描，通过调用算法Rule_Vline得到元件B，再调用算法Rule_Save(A，B)，转步骤1执行；(b)如果当前的搜索方向向右，则通过调用水平向右处理算法Rule_Right，得到当前顶点A的直接后继顶点B，停止对当前顶点A的扫描，再调用算法Rule_Save(A,B)，转步骤1执行。

③ 清空向量S，转步骤1执行。

(2)若当前顶点A为竖直线元件顶点VNode，由于算法的搜索过程是从左向右的，所以只考虑元件的右连接属性，又由前描述可知，AOV图中存储的竖直线顶点是具有直接连接关系并且列值相等、行值最小的竖直线。所以竖直线顶点的搜索方向只有向右和向下，其入度和出度均可能大于1。该种类型的结点在本算法中是处理过程最复杂的部分，也是最关键的部分。算法中涉及到的竖直线元件所有可能的右连接属性如图3所示。其扫描过程如下：

图3 竖直线的右连接属性Fig.3 Right connection properties of vertical line

① 建立向量L，用来保存当前竖直线顶点的直接后继顶点。设置Bool型变量fSpecial为真(true)，用来进行特殊情况处理。根据A的右连接属性(向右→向下)，找到所有可能的搜索方向，将搜索路径存入向量S中。如果向量S不为空，执行步骤②，否则执行步骤③。

② 顺序遍历向量S中的所有路径，若搜索路径存在，则沿搜索路径进行搜索，若不存在，则转步骤③执行。根据搜索方向的不同，分以下两种情况：(a)如果当前的搜索方向向右，则调用水平向右处理算法Rule_Right，得到A的直接后继顶点B，将B保存在向量L中，停止当前方向的扫描；如果当前竖直线的向下连接标志Right_down为假(false)并且向下向右连接标志right_down_right为真，就得到与该竖直线右下右(right_down_right)处连接的元件。若该元件为功能元件B，则将B保存在向量L中，停止当前方向的扫描处理；若该元件为水平线，通过调用水平线处理算法Rule_Hline得到A的直接后继顶点C，将C保存在向量L中，停止当前方向的扫描处理；(b)如果当前的搜索方向向下，得到与该竖直线A相连的下一行的竖直线A1，则执行步骤①，对A1进行扫描处理。如果竖直线元件A1右下右连接属性为真并且A1向右(right)连接属性为假，则设置Bool型变量fSpecial为假。

③ 如果当前竖直线A的右连接属性为假，A的右下右连接属性为真并且Bool型变量fSpecial为真，就得到与竖直线右下右处连接的元件。若该元件为功能元件B，则将B保存在向量L中，停止当前方向的扫描处理；若该处元件为水平线，则通过调用水平线处理算法Rule_Hline得到A的直接后继顶点C，将C保存在向量L中，停止当前方向的扫描处理。

④ 当所有可能的路径都扫描完后，顺序遍历向量L，得到顶点B，调用Rule_Save(A，B)，直至遍历向量L中的最后一个元件为止，清空向量L，转步骤1执行。

(3)若当前顶点A为源顶点SNode，由前可知源顶点只有后继连接关系，其入度为0，扫描过程如下：遍历当前梯级元件链表中所有元件，找出所有列值为0的元件，存入向量L中。遍历向量L得到一个元件B。若B为功能元件，调用Rule_Save(A，B)；若B为水平线，则调用水平线处理算法Rule_Hline得到A的直接后继顶点B，再调用Rule_Save(A，B)。继续遍历向量L，直至处理完向量L中的所有元件，转步骤1执行。

(4)若当前顶点A为尾顶点TNode，则其出度为0，扫描过程如下：遍历顶点数组XList中的所有元件，将类型为输出顶点的元件存入向量S中。遍历S得到一个元件B，调用Rule_Save(A,B)。继续遍历下一元件，直至向量S中的所有元件都处理完为止。

4 转换实例

图4所示为用自主研发的软PLC上位机软件设计的具有复杂串并联关系的梯形图程序。图5对应的是AOV图顶点的扫描过程，图中V**代表竖直线元件。按照从左向右、从上到下的顺序进行扫描，在扫描过程中，竖直线顶点优先，即在扫描过程中，每当碰到有竖直线连接元件的情形，优先处理该列有连接关系的全部竖直线连接元件，并且定义它们所对应的AOV图顶点编号相同，如图5中编号为2或7的顶点。

用转换算法对图5中AOV图顶点进行处理。如实顶点3(I0.2)，按实顶点的扫描规则进行扫描，得到顶点4(I0.3)为顶点3的直接后继顶点，同时将顶点3作为顶点4的直接前驱顶点。又如竖直线顶点7，按竖直线顶点的扫描规则进行处理，找到顶点7有3个直接后继顶点，分别为顶点8(I1.5)、顶点16(I1.6)和顶点22(I2.0)。同时将顶点7分别作为每个后继顶点的直接前驱顶点。当所有顶点都处理完毕后，即生成如图6所示的AOV图。

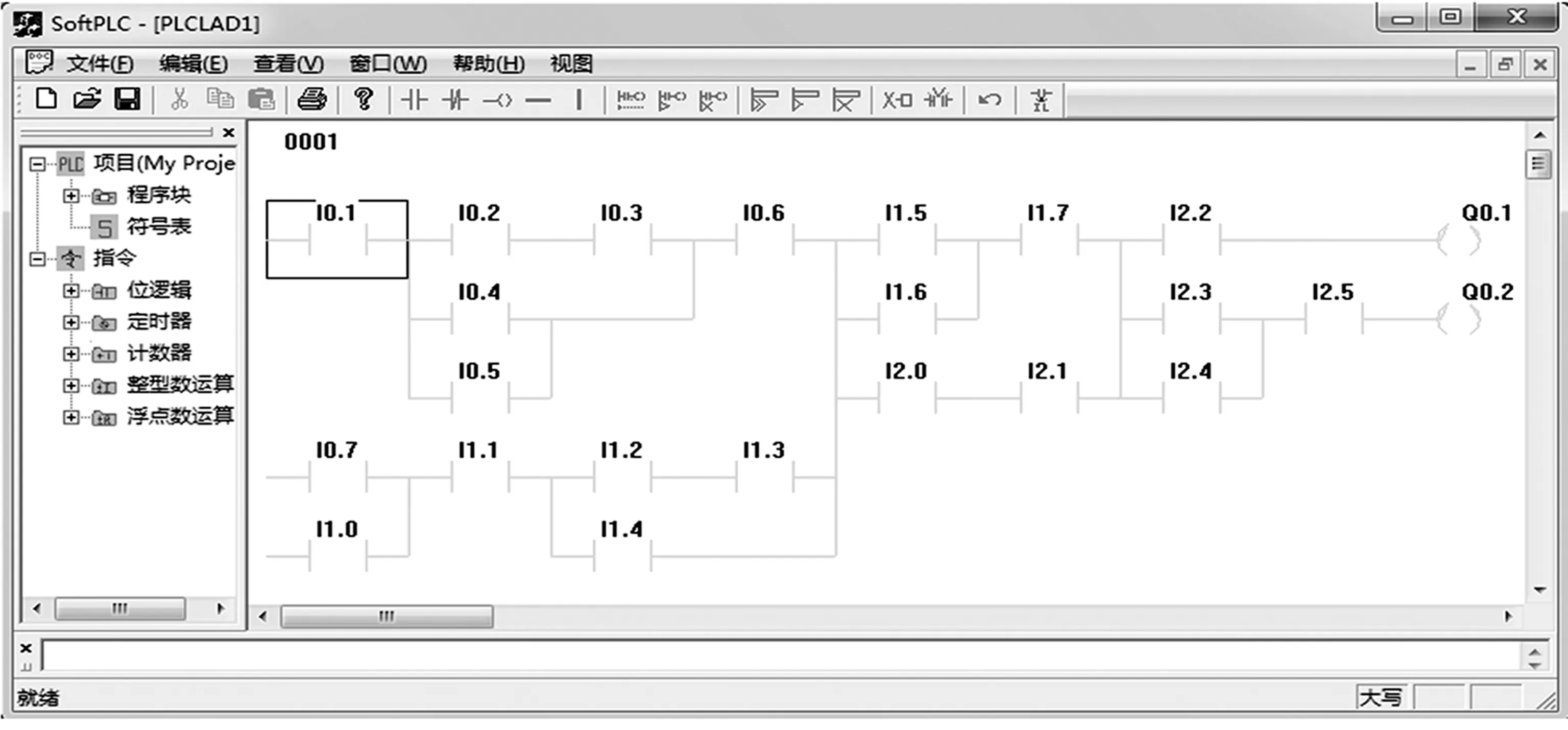
图4 梯形图程序

图5 AOV图顶点扫描过程

图6 转换生成的AOV图

5 与现有转换算法的比较

当前有关梯形图向AOV图转换算法的研究很少，但其主流转换策略均分为顶点扫描、统计顶点的直接前驱和直接后继信息以及AOV图的创建3个过程。本文提出的转换算法与现有转换算

法的流程是一样的，都分三步进行，但具体转换的策略不一样。与现有转换算法相比，本文提出的转换算法具有以下优点：

(1)本文提出的转换算法将竖直连接线元件(并连线)也作为AOV图顶点进行存储，扫描过程简单，省去了现有转换算法中有关虚顶点判断的复杂处理过程，同时节省了顶点扫描的时间。

(2)现有算法中由于顶点直接前驱和直接后继信息的扫描是分开进行的，这就导致每个功能元件顶点至少要处理两次，虚顶点处理的次数要根据并联关系的深度确定，其总的时间复杂度为O(2i+δj)，而本文算法中每个顶点在前驱后继信息的扫描过程中只处理一次，总的时间复杂度为O(i+j)，因此本文提出的转换算法时间复杂度要小于现有转换算法的时间复杂度，尤其是在处理并联关系比较复杂(δ值很大)的梯形图程序时，这种区别更加明显。

6 结语

本文提出的基于迷宫算法思想实现梯形图向AOV图转换的策略，可以简洁高效地实现梯形图各元件直接前驱及直接后继顶点的扫描，进而实现梯形图向AOV图的转换。该策略已经成功应用于自主研发的软PLC上位机软件系统中。为了验证此转换算法的正确性，已进行了很多严格的测试。实例表明，该算法能够高效、正确地将梯形图转换为AOV图。

[1] 马小军. 可编程控制器及其应用[M].南京：东南大学出版社，2007：44-97.

[2] Yan Yi,Zhang Hangping.Compiling ladder diagram into instruction list to comply with IEC 61131-3[J].Computers in Industry,2010,61(5):448-462.

[3] Ge Fen, Wu Ning. A transformation algorithm between ladder diagram and instruction list based on AOV digraph and binary tree[C]∥Hong Kong:2006 IEEE Region 10 Conference,2006:1-4.

[4] 石锐,周雷,杨正益. 软PLC梯形图到语句表转换新策略的研究[J]. 计算机工程与应用, 2010,46(18):244-248.

[5] 邹莉. 软PLC梯形图向指令表转换新算法的研究与实现[J]. 聊城大学学报：自然科学版， 2013,26(1):105-110.

[6] 冯光，夏清国，裴元方. PLC梯形图向AOV图的一种转换方法[J]. 航空计算技术，2009，39(2)：109-112.

[7] 阳俊将，黄道平，刘少君. 关于PLC梯形图到指令表转换算法的研究[J]. 信息技术, 2012(6): 75-78.

[8] 严蔚敏，吴伟民. 数据结构[M]. 北京：清华大学出版社，1997:50-166.