股票价格波动与宏观经济关系的理论和实证探讨

赵东越，曾 成

(1.山东大学，山东 济南 250100；2.爱丁堡大学，英国 苏格兰 爱丁堡市)

一、问题的提出

世界各国的证券市场都会不可避免地受到宏观调控的影响，中国股票市场作为一个发展仅有20余年的新市场也有不成熟的一面，曾经出现过很多针对股市的调控措施，学者对股市作为宏观经济晴雨表的作用以及宏观政策是否与股票市场挂钩存在争议。本文在理论分析的基础上用向量自回归和误差修正模型来研究股票市场与宏观经济变量之间是否存在关联性以及存在怎样的关联性，从而把握宏观经济变量对股票市场的作用机制。

1976年罗斯[1]提出了APT(Asset Pricing Theory)理论，该理论认为宏观经济变量与风险是影响股票市场的因素，这使得股票市场与宏观经济变量的相互关系有了理论依据。从此，股票市场与宏观经济变量的相互影响关系就成为学者们研究的热点问题。股票市场的发展壮大不仅增强了资本市场的活动能力，也在一定程度上反作用于实体经济，对宏观经济各变量产生影响，再由宏观经济变量反作用于股票市场而如此循环往复。政府采取的宏观经济调控手段，也是基于这样的作用机制来对资本市场和实体经济进行调节的。

Patrick[2]认为在经济发展初期, 金融发展导致实际部门的增长, 当经济趋于成熟时, 经济发展反过来促进金融发展。Chen 等人[3]在APT 的基础上建立了一个向量自回归(VAR)模型，他们发现宏观经济变量通过影响贴现率成为股市风险因素之一，还发现宏观经济变量和股票价格之间存在长期的均衡关系。Caporaleg[4]对东亚国家的实证研究也表明, 资产价格变动能导致产出增长波动。Levine和Zervos[5]用股市交易规模、成交量、交易率、经济一体化水平和股市波动率等指标来衡量股市发展水平，并对GDP增长和资本形成率进行回归分析，研究发现股市与宏观经济之间存在高度的正相关关系。Atjer和Jovanovic[6]以包括发达国家和发展中国家在内的40个国家为样本, 利用GJ 模型成功验证了股市与经济有明显的相关关系。Granger[7]提出了协整分析理论，为检验宏观经济变量与股市的关联性提供了另一种方法。Fama[8]用多因素模型证实了美国经济中货币供应量与通货膨胀率对股市收益率有显著影响，并指出货币供应量、通货膨胀是通过影响实体经济增长来对股市产生作用的。Bennanke 和Kuttner[9]利用VAR 方法，考察了未预期货币政策对股票市场的影响。实证结果表明，货币政策对股票市场有影响，但货币政策的变动只能解释部分股票价格的变动。钟小强[10]利用VAR 模型和协整理论就货币政策对股市的有效性进行实证检验，结果表明股指和货币供应量、利率之间存在稳定的长期均衡关系；同时货币供应量是股指的格兰杰原因，利率不是股指的格兰杰原因；相对于利率，货币供应量对股市的影响更大。孙云玉[11]采用2000年—2007年的数据分析中国股市价格波动与货币供应量之间的关系，结果表明二者之间存在着长期稳定的均衡关系。

也有学者认为股市与宏观经济之间关系较弱，甚至没有关系。例如，Harris[12]选取了49个国家作为样本国, 采用二阶段最小平方法进行检验, 发现股市流动性的增强促进了交易成本的降低和风险的分散, 但这也增加了资产二级市场的活动水平, 从而将投资者的新增资本吸引到既有资产的购买上，而不是促进新的资本形成，这种储蓄转流便成为经济增长的极大障碍，因此股市发展和经济增长之间的关系较弱，并且在统计上不显著，尤其是欠发达国家，股市发展与宏观经济关系非常弱。Arestis和Demetriades[13]认为股市缺乏效率, 难以与宏观经济有密切关系。

以上研究均是从实证的角度来证实股市与经济增长之间的关系, 但是由于参数选择不一致, 导致结论截然相反, 并且实证结论缺乏理论支持。本文认为仅仅用实证分析的方法研究股票价格波动与宏观经济的关系是不够的，因此，本文将消费资产定价模型和生产者理论结合起来，对股票价格与经济增长之间的关系进行理论分析。

二、股票定价模型

现实中，常常遇到与时间有关的经济状态，经济状态与时间的关系叫作路径。决策者需要从众多的路径当中选择一条最优路径，当变量沿着该路径变化时，目标函数达到最大值。因此，动态最优化问题与静态最优化问题的不同之处主要在于，静态最优化问题的解是点，与时间无关，而动态最优化问题的解是一条依赖于时间的路径，实际上是一条曲线或者是一个集合。一般来说，这类问题可以分两种情形来讨论。第一种情形是时间是离散的，即将一段时间划分为几个不同的区间，可以是有限的，也可以是无限的。第二种情况是时间是连续的，时间变量的定义域是连续区间集合。

对于离散时间的最优化问题，一般来说常用的方法有两种：一种是拉格朗日乘数法，即将动态问题看成是多变量的静态问题；另一种是贝尔曼方程，即将最优化问题变成一个两期问题求解。

现代生命周期理论是由安迪和莫迪利安尼[14]在20世纪60年代前后创立的，其最初形式是确定性的，后来在理性预期学派的影响下，大约在1978年，由Hall[15]成功地给出了生命周期函数的现代形式，即随机的生命周期函数。该理论解决了现时消费与未来消费或储蓄之间、同一时期不同类型储蓄资产之间的配置关系。为说明现代生命周期理论，可以假设将消费者一生效用写成如下形式：

Ut=Et[F(Q1,Q2,…,Qt,…,QT)]

(1)

其中，Ut是t时期的效用，Et是在t时期利用了所有可得到的信息的(理性)预期算子，(Q1,Q2,…,Qt,…,QT)表示时刻1到T的消费品向量，F(·)是一个对其各自变量均非递减的凹函数。该函数计算的效用是在确定性条件下从消费向量得到的，代表了消费者一生中的消费效用，下标表示年龄的大小，1表示出生日，T表示死亡日。因为决策是在未来不确定情况下作出的，所以，预期算子表示消费者的偏好目标是期望效用。为了简单起见，设效用函数满足时际可加性条件，即Ut可以写成：

(2)

消费者一生效用最大化问题可以归为两个问题：一是在价格给定条件下每个时期的及时效用函数V(Qt)的最大化问题；二是整个生命周期内总效用函数的最大化问题。

t时期的即时效用最大化是指在时间给定的条件下如何分配t时的总支出，无需考虑跨时支出的总量。该问题的目标函数和约束条件见式(3)和式(4)。

目标函数：maxVt(Qt)

(3)

约束条件：PtQt=Ct

(4)

其中，Pt是对应于Qt的价格向量，Ct是t时期的消费支出总额,由下一步的时际选择问题决定。

用φ(Ct,Pt)表示t时期的间接效用函数(即时效用最优化的结果)，rt表示实际利率，则跨期最优化问题就可以改写成式(5)和式(6)。

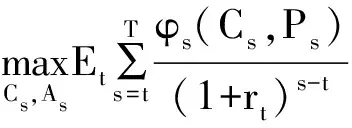
(5)

约束条件： At+1=(At+Yt-Ct)(Pt+1+dt+1)/Pt(其中t=1,2,…,T)

(6)

建立拉格朗日函数如下式：

(7)

一阶条件为：

(8)

(9)

(10)

可得欧拉方程：

(11)

该模型常又被称为消费资产定价模型。欧拉方程表示现在消费和未来消费的边际替代率应等于资产的相对价格。该方程将消费者决策置于跨时期的框架里，有助于认识预期资产报酬与货币利率之间的关系。

我们进一步假设企业资本K的成本是R，产出Y的生产函数为：

Y=AKα

(12)

企业的利润函数为：

(13)

Rs=αAKsα-1

(14)

ds=ROEs=RsK=αYs

(15)

(16)

(17)

根据费雪公式实际利率近似等于名义利率减通货膨胀率，注意到利率平价模型为：

(18)

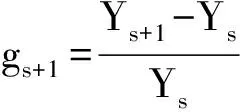
三、股票价格、经济增长与货币政策的实证分析

(一)模型的设定与变量的选取

以上理论模型告诉我们，股票价格与经济规模、经济增长率、利率、通货膨胀率、货币政策等因素有关。在开放条件下，国内利率、货币发行量、利率还与汇率和国际收支有关。一般来说，动态最优化的一阶条件是二阶非线性动态系统，很难获得它们的解析表达式。作为一种次优选择，可以利用泰勒展开式对非线性系统稳定状态附件进行线性化处理，得到一个向量自回归模型 (VAR)。通过对向量自回归模型的计量分析，判断股票价格与经济增长、货币政策、汇率之间是否有长期均衡关系，从而估计股票价格偏离均衡状态的程度。

非限制性的k维向量自回归模型VAR(k)可表示为：

(19)

这里，A1、A2、…、Ak都是k×k参数矩阵,Bi是k×m参数矩阵，Et是k×1随机误差向量，Ei=iidN(O,),O是k×1零向量，是k×k协方差矩阵。

将表达式(19) 改写为下列向量误差修正模型的形式:

(20)

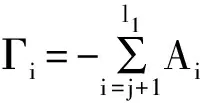
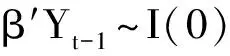
实证分析包括以下几个步骤: 第一步，检验时间序列的平稳性。如果不存在单位根说明过程是平稳的；如果存在单位根，再对变量的一阶差分或高阶差分进行单位根检验。第二步，如果有几个序列不是平稳的，则它们之间可能存在协整关系。一般来说，协整关系是随机变量之间的长期均衡关系。如果要考察单整序列之间的长期均衡关系，则需要检验对协整关系的存在性。第三步，如果协整检验证明几个单整变量之间存在协整关系，则用VEC模型将长期均衡关系和短期调整方程估计出来，再进行分布滞后项和误差修正项对向量的短期变动的因素分析。

从理论上讲，误差修正模型可选择的变量包括上证指数、经济增长率、利率、货币发行量和汇率。考虑到物价、汇率、货币、工业增加值都有月度数据，样本容量比较大，而经济增长率没有月度数据，只有年度和季度数据，且1996年之后才有季度数据，如果采用季度数据就必须舍弃很多有价值的数据，因而我们采用月度数据，经济增长率的指标就用工业增加值增长率代替。由于利率没有实现市场化，因而用广义货币M1代表货币政策指标。我们用国际清算银行公布的实际有效汇率表示开放因素的影响。这样，在向量误差修正模型的分析当中，纳入上证指数、工业增加值、货币、汇率、商品零售物价指数。零售物价指数的增长率代表通货膨胀率。检验发现它们都是平稳的，因此在误差修正模型中把上证指数、实际有效汇率和货币发行量都看成非平稳时间序列模型的内生变量。

模型中的相关变量定义如下：SZ为上证指数，REER为人民币的实际有效汇率，GYG为同比工业增加值增长率，PPI为同比商品零售价格指数，logM1为狭义货币供应量的对数， Yt=(SZ,REER,logM1)′为内生向量，Xt=(GYG,PPI)′为外生变量。SZ、REER、LOG(M1)、PPI和GYG的变化如图1所示。

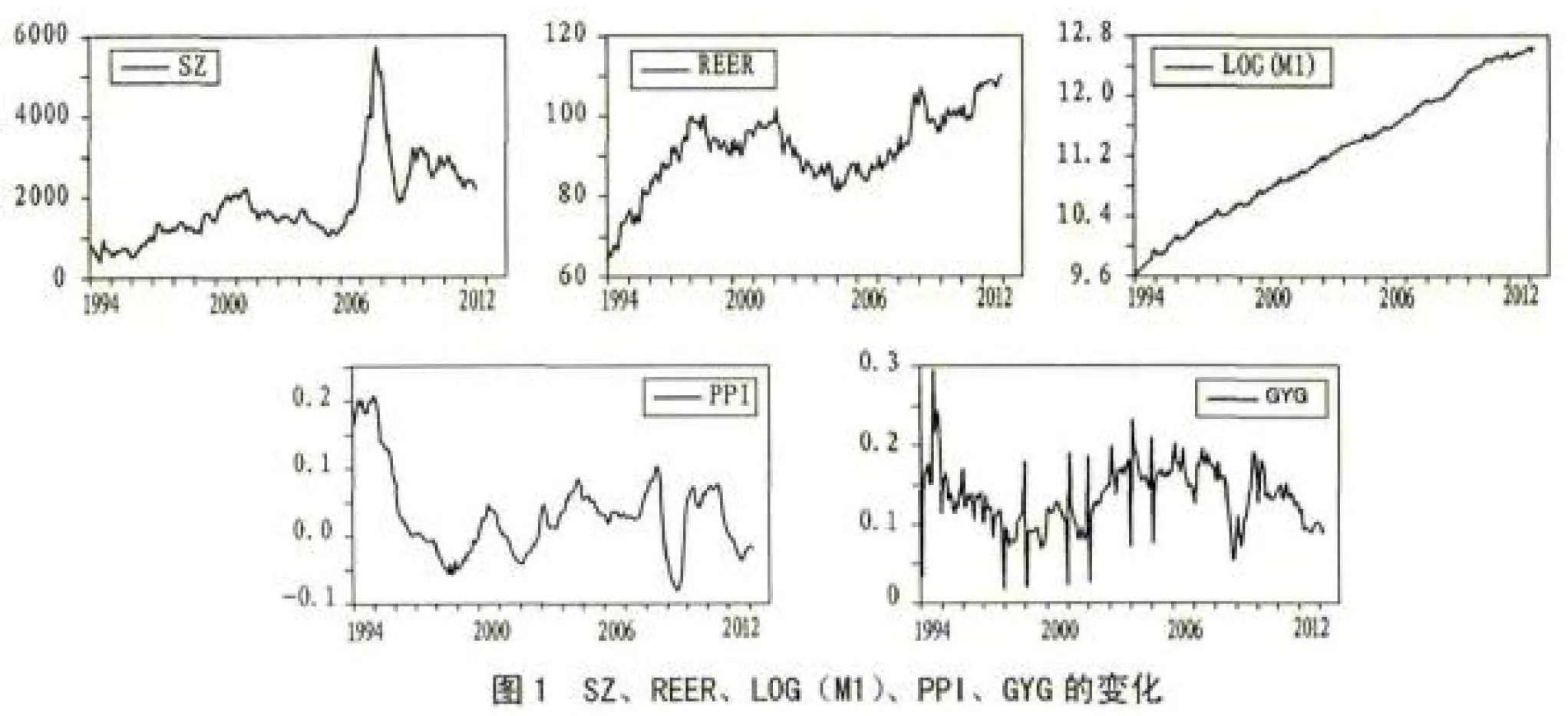
(二)平稳性检验

上述5个水平变量的ADF单位根检验表明：第一，工业增加值的增长率GYG是平稳的(见表1)；第二，物价指数PPI是平稳的(见表2)；第三，上证指数SZ是非平稳的(见表3)；第四，实际有效汇率REER是非平稳的(见表4)；第五，广义货币M1是非平稳的(见表5)。

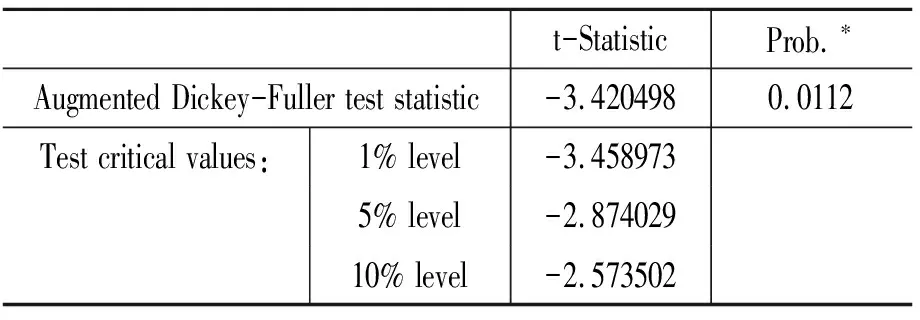
表1 零假设: GYG有单位根

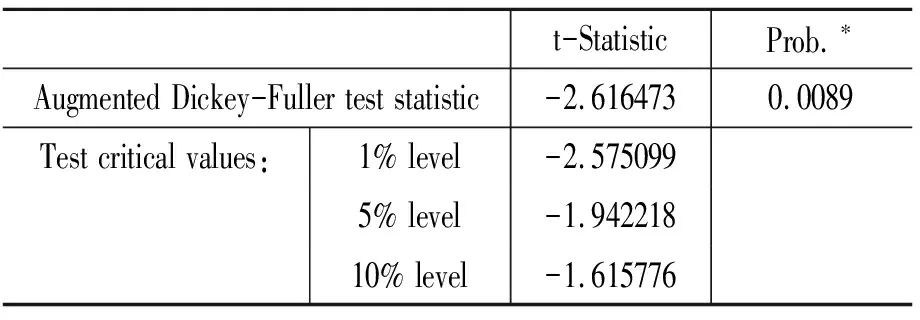
表2 零假设: PPI有单位根

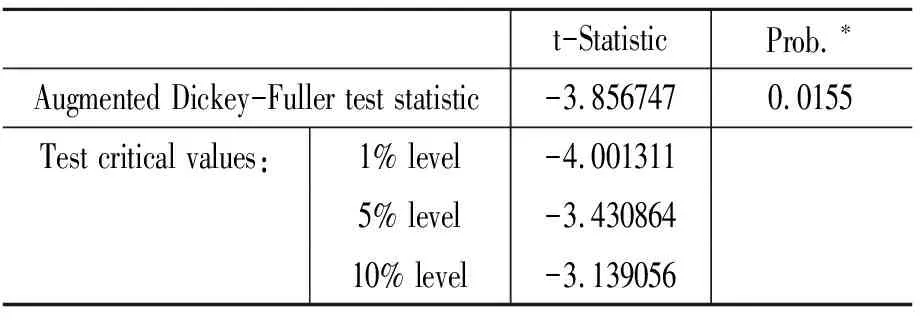
表3 零假设: SZ有单位根

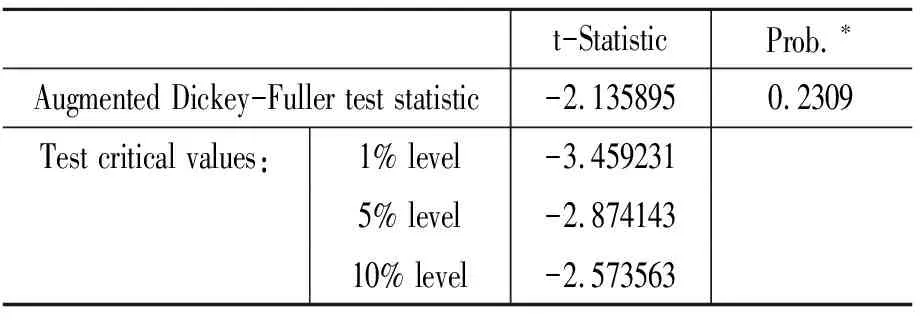
表4 零假设: REER有单位根

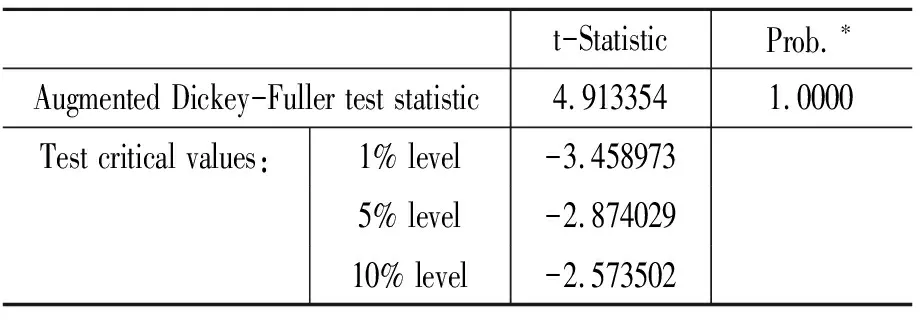
表5 零假设: M1有单位根

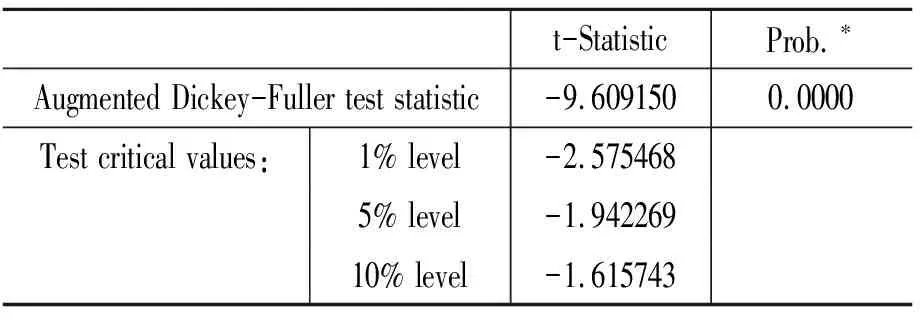
表6 零假设: DSZ有单位根

再对SZ、REER、logM1的差分进行单位根检验(见表6、表7、表8)，结果表明SZ、REER、logM1的差分都是平稳过程，即SZ、REER、logM1都是一阶单整I(0)过程。

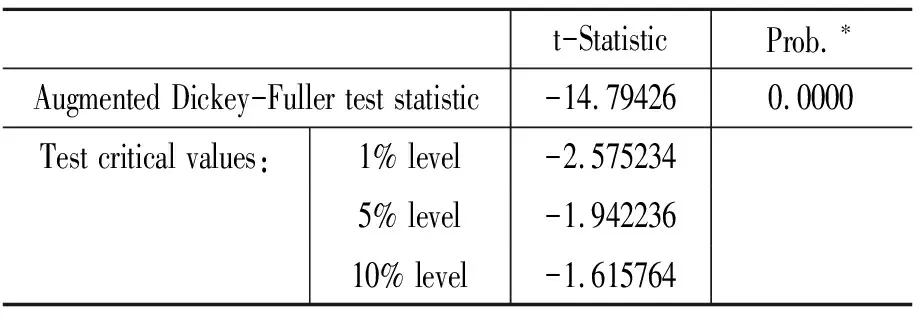
表7 零假设: DREER有单位根

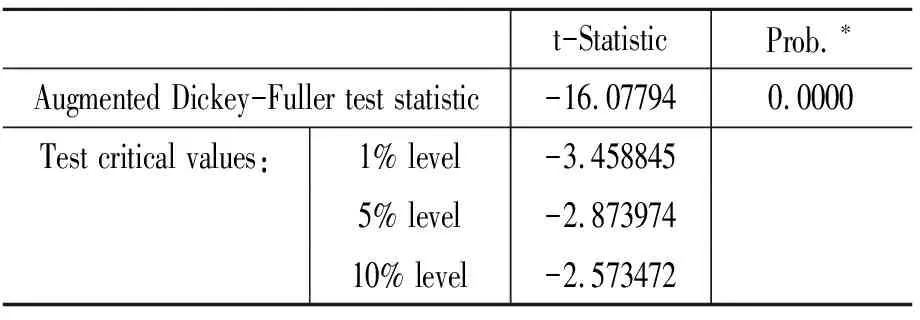
表8 零假设: DlogM1有单位根

(三)协整检验

由于SZ、REER、logM1都是单整过程，而经济理论表明它们之间有一定的关系，因而接下来我们将检验三者之间是否存在协整关系。本文采用非限制性协整秩检验，结果表明存在协整关系，而且协整关系至少有2个(见表9)。

表9 非限制性协整秩检验

(四)向量自误差修正模型

大部分有关宏观经济的模型都是利用经济理论来建立变量之间关系的联立方程模型，但是经济理论通常并不足以对变量之间的动态联系提供严密的说明，而且内生变量既可出现在等式的左端又可出现在等式的右端，这使得估计和推断更为复杂。为解决这些问题，学者们创造了一种用非结构性方法来建立各变量之间关系的模型，就是向量自回归模型(VAR)。向量自回归模型通常用于相关时间序列系统的预测和随机扰动对变量系统的动态影响研究，对宏观经济变量这一时间序列的相关分析具有较好的预测和解释能力。

D(SZ)=-0.04×[SZ(-1)-166.36×REER(-1)+13377.20]+41.19×{LOG[M1(-1)]-0.24×REER(-1)+ 10.89}+0.37×D[SZ(-1)]+0.03×D[SZ(-2)]-450.3×D{LOG[M1(-1)]}-38.66×D{LOG[M1(-2)]}+1.41×D[REER(-1)]+2.36×D[REER(-2)]+3.44+207.36×GYG-716.35×PPI

[LOG(M1)]=1.21E-06×[SZ(-1)-166.36×REER(-1)+13377.20]+3.18E-04×{LOG[M1(-1)]-0.24×REER(-1)+10.89}+1.08E-05×D[SZ(-1)]+6.11E-06×D[SZ(-2)]-0.07×D{LOG[M1(-1)]}-0.26×D{LOG[M1(-2)]}+9.52E-04×D[REER(-1)]-2.22E-03×D[REER(-2)]+0.02-6.29E-03×GYG-2.91E-03×PPI

D(REER)=2.63E-04×[SZ(-1)-166.36×REER(-1)+13377.2029503]+0.03×{LOG[M1(-1)]-0.24×REER(-1)+10.8908276869}+9.08E-05×D[SZ(-1)]-1.81E-03×D[SZ(-2)]+11.13×D{LOG[M1(-1)]}+4.98×D{LOG[M1(-2)]}+4.04E-03×D[REER(-1)]-0.14×D[REER(-2)]+1.10-8.79×GYG+3.62×PPI

我们分别用1个或2个协整方程去估计向量误差修正模型，最终选1个协整方程的误差修正模型如下：

D(SZ)=3.40E-03×[SZ(-1)+0.05×M1(-1)-681.385×REER(-1)-21341.73×PPI(-1)-116402.35×GYG(-1)+72125.385]+0.38×D[SZ(-1)]+0.04×D[SZ(-2)]-3.65E-03×D[M1(-1)]-9.64E-04×D[M1(-2)]-2.72×D[REER(-1)]-1.13×D[REER(-2)]-1560.51×D[PPI(-1)]-85.47×D[PPI(-2)]+496.73×D[GYG(-1)]+337.05×D[GYG(-2)]+8.89

其中，协整方程为：

SZ(-1)+0.05×M1(-1)-681.385×REER(-1)-21341.73×PPI(-1)-116402.35×GYG(-1)+72125.38=0

通过计量分析发现, 上证指数与经济增长率、通货膨胀率和汇率之间存在长期稳定的协整关系, 且随着三者的提高, 股票指数也相应上升，即呈正向波动关系。工业增加值增长率上升、商品价格上升、人民币汇率上升说明市场情况良好，上证综指也会上升。上证指数与货币供应量成反向相关关系，而工业增加值增长率、商品价格和人民币汇率三者互为反向波动，两变量一个增加另一个减少。上证指数的上升也会导致工业增加值增长率、商品价格和人民币汇率上升，使货币供应量下降。货币供应量的上升会使工业增加值增长率、商品价格和人民币汇率上升。

四、结论

通过以上理论分析和实证研究, 我们发现我国的宏观经济变量与股市之间存在着相互影响的关系。宏观经济变量除了可以单独影响股市外，还可通过相互作用共同影响股市。它们通过各自的作用机制，直接或者间接地影响股票市场。同时，股市也可反作用于宏观经济。宏观经济变量对股票市场的具体影响为：工业增加值增长率、商品价格、人民币汇率与上证指数同向变动，货币供应量与上证指数反向变动。目前我国的股票市场还处于不成熟阶段，容易受各种因素的影响而使价格波动频繁，这就增加了中央银行对货币供应进行有效调控的难度，使货币调控一般是逆周期操作并有一定的滞后性。当货币供应增加超过民众因经济增长及支付习惯和制度等变动引起的需求增加时，市场利率会下降，就会促使部分资金流入股票市场，从而提高股市成交量和成交金额。当股市扩容有限时，股价就将上涨。可见，货币变动领先于股价变动，且两者之间是正相关关系。货币供给增长会刺激经济增长，使企业现金流增加，从而提高股票价格。但货币供给增加有可能导致流通中的货币过多，这在一定程度上又会导致通货膨胀，从而引发紧缩性货币政策，使资产价格向相反方向运动。从长期看，股价指数和货币供给出现反向变化。这些实证结论与前面的理论假定大体是一致的，但是也出现了与实际情况相出入的地方。

参考文献：

[1]Ross, S. Arbitrage Theory of Capital Asset Pricing[J].Journal of Economic Theory,1976,(13):341～360.

[2]Patrick,HT. Financial Policies and Economic Growth in Underdeveloped Countries[J].Economic Development and Cultural Change，1966，(2)：174～189.

[3]Chen N F,Roll R,Ross S A. Economic Forces and the Stock Market[J].Journal of Business，1986，(3)：383～403.

[4]Caporaleg.M.,Spagnolon. Asset Price and Output Growth Volatility: the Effects of Financial Crises[J].E-economics Letters，2003，(1)：69～74.

[5]Ross Levine,Sara Zervos.Stock Markets, Banks, and Economic Growth[J].The American Economist，1998，(3)：537～558.

[6]Atjer, Jovanovic B. Stock Markets and Development[J].European Economic Review，1993，(37)：632～640.

[7]Granger.C.W.J. Testing for Causality: Personal Viewpoint[J].Journal of Economic Dynamics and Control，1981，(2)：329～352.

[8]Fama, E. Stock returns, Expected Returns, and Real Activity[J].Journal of Finance,1990,(45)：1089～1090.

[9]Bernanke, Ben S.,Kenneth N.,Kuttner.What Explains the Stock Market’s Reaction to Federal Reserve Policy?[J]. The Journal of Finance,2005，(3)：1221～1257.

[10]钟小强.股市对货币政策敏感性的实证分析[J].广西金融研究，2008，(4)：40～43.

[11]孙云玉.股市价格、货币供应量与货币政策——基于中国2000年—2007年数据的实证分析[J].南京审计学院学报，2009，(2)：51～56.

[12]Harris Richard DF.Stock Markets and Development: A Reassessment[J].European Economic Review，1997，(1)：139～146.

[13]Aretis P,Demetriades P. Financial Development and Economic Growth: Assessing the Evidence[J].The Economic Journal，1997，(107)：783～799.

[14]Ando Albert, Franco Modigliani.The Life-Cycle Hypothesis of Saving: Aggregate Implications and Tests[J].The American Economist，1963，(1)：55～84.

[15]Hall Robert.Stochastic Implications of the life Cycle-Permanent Income Hypothesis:Theory and Evidence[J].Journal of Politics，1978，(6)：971～987.