基于MPI的OBC三维多波多分量地震观测正演模拟并行算法实现
周 丽,顾汉明,成景旺,刘春成,刘志斌,杨小春
(1.中国地质大学(武汉)地球物理与空间信息学院,湖北武汉430074;2.中国地质大学(武汉)地球内部多尺度成像湖北省重点实验室,湖北武汉430074;3.长江大学地球物理与石油资源学院,湖北武汉430100;4.中海油研究总院,北京100027)
海上多波多分量地震勘探采用海底OBC采集方式,将检波器安置在海底接收。该检波器内部包含了压力检波器(水听器)和3个相互垂直的速度检波器(X分量、Y分量和Z分量),因此也将海上多波多分量技术称为海上四分量(M4C)地震勘探技术[1]。这种采集方式不仅能够接收传统的纵波,而且能够接收横波以及转换波,是真正意义上的全波勘探,可以携带更加丰富的海底信息。目前为止M4C技术已解决了海上勘探中的多个难题[2-5]。
海上作业实验成本高,耗时费力,所得出的观测系统参数不具有完备性。而基于三维波动方程的并行数值模拟不仅能够快速模拟复杂介质中波的传播特征,而且能模拟各种不同的观测系统参数下的炮集记录,基于模拟记录的偏移成像处理效果优选观测系统参数。三维交错网格有限差分由于其占内存小、模拟精度高、易于并行等优点已被很多学者用于复杂介质的地震正演模拟中。Virieux[6-7]使用了时间二阶精度和空间二阶精度的交错网格有限差分格式,对一阶应力-速度方程进行了差分离散,模拟了P-SV波和P-SH波的传播;Levander[8]在空间和时间都为二阶精度的基础上,将空间上的有限差分格式改为四阶,而时间仍保持二阶精度,将模拟精度进一步提高;董良国等[9]首先进行了一阶弹性波方程的交错网格高阶有限差分模拟,推导了高阶有限差分的格式,给出差分格式的稳定性条件;裴正林[10-11]将交错网格有限差分引入到了三维中,进行了三维各向同性介质和各向异性介质中弹性波的模拟。
三维地震波波动方程数值模拟对计算机的内存要求很大,目前单版PC机不能满足较大规模的正演计算,尤其是适应海上宽方位OBC地震采集的正演模拟。大型的并行计算机、对称多处理机、分布式共享存储处理机、PC-Cluster集群以及图形处理器(Graphic Processing Unit,GPU)计算等的出现,都为地震数值模拟提供了一个很好的计算平台。其中PC-Cluster集群搭建方便,运算性能好,相对来说较廉价,已经成为了高性能的主流产品[12]。常用的并行模式主要有MPI和并行虚拟机(Parallel Virtual Machine,PVM),其中MPI是目前广泛使用的并行编程工具,它具有移植性好、功能强大、高效实用等多种特点[13]。MPI是一个库,共有上百个函数调用接口,目前广泛使用的为OPENMPI和MPICH,本文的并行计算是在MPICH2平台上实现的。
并行计算为大规模的三维地震数值模拟注入了新的活力。Furumura等[14]采用了伪谱法与有限差分混合并行法对1999年的台湾天然地震进行了模拟;Bohlen[15]采用交错网格有限差分法进行了粘弹介质的波动方程模拟;Micikevicius[16]使用CUDA(Compute Unified Device Architecture)平台实现了三维有限差分的GPU计算;王德利等[17]采用了Bohlen的方法进行三维粘弹介质的地震波场并行模拟;王月英[18]采用有限元法进行了声波波动方程的并行计算;何兵寿等[19]从二维弹性波动方程出发,给出了适用求解的计算空间划分方法及通信方案;魏星等[20]和秦艳芳等[21]结合伪谱法和有限差分的各自优点,在X和Y方向使用伪谱法计算,在Z方向使用交错网格计算,并在Z方向上进行了并行设计;公续飞等[22]描述了三维弹性波有限差分法的GPU实现方法;段玉婷等[23]对精细积分法的实现过程进行GPU并行,实现了三维地震正演模拟;张明财等[24]基于MPI进行了三维瑞雷波的有限差分并行模拟。
我们针对海底OBC采集特点,采用基于MPI的交错网格有限差分法进行了海上OBC三维地震多波多分量地震观测的正演模拟,并行设计中将计算任务沿X,Y,Z3个方向分配成多个子区域,每个子区域采用一个进程进行计算,通过简单的3层模型验证该并行方案的效率,最后进行了海上某靶区OBC多波多分量地震观测的正演并行数值模拟。
1 三维弹性波方程的有限差分正演算法
在三维各向同性介质中,利用交错网格有限差分法进行正演模拟时采用的波动方程形式为一阶应力-速度方程,其可以表示为
(1a)
(1b)
式中:vx,vy和vz表示速度分量;σij(i,j=x,y,z)表示应力分量;λ和μ为拉梅常数。在交错网格有限差分中,变量的导数是在相应的变量网格半节点上计算的。为了保证在空间上具有偶数阶精度,弹性参数以及波场分量的空间分布如表1和图1所示。其中正应力σxx,σyy和σzz置于节点(i,j,k)上;剪应力σxy,σxz和σyz分别置于节点(i+1/2,j+1/2,k),(i+1/2,j,k+1/2)和(i,j+1/2,k+1/2)上;速度分量vx,vy和vz分别置于节点(i+1/2,j,k),(i,j+1/2,k)和(i,j,k+1/2)上。同时保证在时间上具有偶数阶精度,应力分量在半时刻t+Δt/2取值,速度分量在整时刻t取值。波动方程中一阶空间导数采用公式(2)的离散格式[25]:
(2)
(3)

表1 弹性波波场分量和弹性参数的空间位置

图1 交错网格应力分量与速度分量的空间位置
PML完全匹配层法主要衰减沿着模型边界法向方向传播的地震波,不衰减平行于模型边界传播的地震波。完全匹配层法最主要的是衰减因子的求取,本文衰减因子d(x)的计算如下:
(4)
式中:vPmax为最大纵波速度;δ和R分别表示PML层的宽度和理论反射系数。根据PML的方程分解思路,设v=v‖+v⊥,σ=σ‖+σ⊥,且dx,dy和dz分别为X,Y,Z方向上的阻尼因子。以vx变量为例(其它变量类推),三维各向同性介质中最佳匹配吸收边界条件可以表示为

(5a)
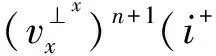
(5b)
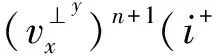
(5c)
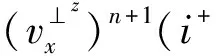

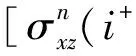
(5d)
2 基于MPI的三维并行计算的整体设计
三维弹性波正演模拟中,速度分量和应力分量一共有9个变量,再加上密度ρ和拉梅常数λ,μ,则在正演过程中至少要申请12个三维数组,假设每个变量采用双精度浮点数占8个字节且三维模型空间网格数为Nx,Ny,Nz,则计算过程中一共需要申请的内存大约为Nx×Ny×Nz×12×8个字节。可见三维弹性波正演所需内存很大,尤其是在模型较大的时候,单个PC机根本无法进行计算,必须通过并行将所需内存划分到多个子空间中分别存储,才能实现三维波动方程的求解。
交错网格有限差分格式中,无论是速度分量还是应力分量,任何网格点处波场值的计算只需要周围有限个点即可,因此计算过程具有良好的局部性,非常有利于并行计算。计算过程中,可将整个模型分成多个子区域进行计算,所有子区域并行执行,各个子区域只需要交换子区域边界处的波场值便能达到整个模型的并行计算。
2.1 三维并行相邻进程的交换设计
假设正演模型网格数为N=NxNyNz,其中Nx,Ny,Nz分别为X,Y和Z方向的网格点数。并行计算中,假设X,Y,Z方向分别采用Px,Py,Pz个进程计算,则总的计算进程数为Nproc=PxPyPz,每个子空间计算网格数为Npe=N/Nproc。计算所需内存被分配到Nproc个子空间上,每个子空间具有自己独立的内存空间。由此可见,除了由于通信需要,每个子空间边界需要增加的网格点数以外,该并行方案在计算过程中不重复占用空间,程序并没有因为并行增加额外的巨大的内存空间。
若有限差分过程中空间导数采用2N阶高阶精度,则根据交错网格有限差分格式,每个子空间在X,Y,Z3个方向均需要增加N个网格点作为缓冲过渡层,用来与相邻子进程间进行通信与交换,保存从相邻子空间交换得来的数据。图2为三维并行过程中相邻子空间的数据通信示意图,每个子空间均需要和周围的上、下、左、右、前、后6个子空间进行交换。图2中浅灰色部分表示发送源地址,深灰色部分表示接收地址。并行计算过程中,将所有计算进程按X,Z,Y的方向顺序依次进行标识排序,则每个进程对应一个标识myid。同时设置一个三维进程坐标系,其中X,Y,Z方向的取值范围分别为:0~Px-1,0~Py-1和0~Pz-1,因此每个进程对应一个三维坐标,那么X坐标为0的子模块左边界、X坐标为Px-1的子模块右边界、Y坐标为0的子模块前边界、Y坐标为Py-1的子模块后边界和Z坐标为Pz-1的子模块下边界要用吸收边界条件,而Z坐标为0的子模块上边界采用吸收边界条件或自由边界条件。同时这些边界处的衰减因子d(x)按照公式(4)计算,而每个进程的其它边界则令d(x)=0。
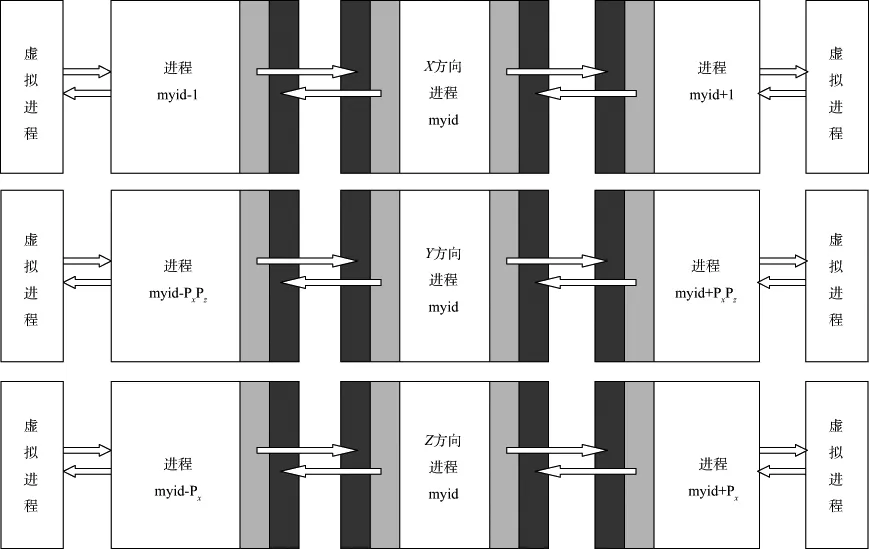
图2 三维相邻进程交换示意图解
现假设某一进程标识号为myid,则与该进程交换的周围6个进程的标识号分别为myid-1(左)、myid+1(右)、myid-Px(上)、myid+Px(下)、myid-PxPz(前)和myid+PxPz(后)。有的进程(当X坐标为0或Px-1,Y坐标为0或Py-1,Z坐标为0或Pz-1)的某些相邻进程不存在时,则引入虚拟进程MPI_PROC_NULL。虚拟进程是不存在的假想进程,在MPI中的主要作用是充当真实进程通信的目或源。当一个真实进程向一个虚拟进程发送数据或从一个虚拟进程接收数据时,该真实进程会立即正确返回,如同执行了一个空操作。
2.2 基于MPI的海上OBC地震观测并行模拟计算流程
结合交错网格有限差分格式以及海上OBC观测系统的特点,设计了并行计算流程。
1) 首先,调用MPI初始化程序,启动并行计算环境,并获取进程序号以及总的计算进程个数Nproc。
2) 主进程(0进程)读取正演相关参数、震源文件以及接收点文件。其中正演参数包括时间步长、空间步长、震源主频、单炮记录时间长度、各个方向进程个数(Px,Py,Pz)。判断正演稳定性条件是否满足,以及总的计算进程PxPyPz是否等于Nproc,如果不满足这些条件,则重新修改参数。
3) 各个进程读取相应的模型纵、横波速度值和密度值,并根据读取的纵、横波速度和密度求取拉梅参数等。根据横波速度值(横波速度由0值变成非零值的分界处)求取每个接收点对应的Z方向海底位置,用来保存海底OBC的波场值;同时计算该进程的三维坐标,根据坐标值判断每个进程的哪些边界需要进行边界条件的处理以及使用哪种边界条件(自由边界条件还是PML边界条件)。
4) 时间循环开始,判断震源属于哪一个进程,则在该进程对应的网格点上加入震源函数。
5) 各个进程速度场并行计算,同时根据步骤3)的判断,进行边界的处理。将需要交换的边界处的速度场保存至交换缓冲区,然后和周围的6个进程进行交换,以便进行下一个时刻的应力场的计算。交换过程中,首先确定需要交换的周围6个进程的标识号,然后调用标准非阻塞通信进行进程之间的数据交换与通信。
6) 同步骤4)一样,进行应力场的计算。
7) 判断各个进程中各个接收点所在位置,进行波场信息规约,输出指定时刻的快照,保存该时刻接收点的波场值。判断时间循环是否结束,若没有结束,跳出步骤4)继续计算。
2.3 并行效率分析
本次并行测试所使用集群的硬件环境配置为:①管理节点一个,计算节点30个;②节点CPU为Intel(R)Quad Core E5520 Xeon(R) CPU,2.26GHz×2,8核;③内存为16GB(4×4GB),1066MHz;④磁盘采用15T磁盘阵列。
通过一个简单的三维层状模型(图3)来进行并行设计的效率性分析。该模型大小为3000m×2400m×1800m,网格数为Nx=600,Ny=480,Nz=360,空间步长dx=dy=dz=5m,时间步长dt=0.5ms,记录长度选取2s,正演过程中采用空间4阶、时间2阶计算精度,震源采用30Hz的雷克子波,且激发点位于(1500m,1200m,150m)处,模型周边均使用吸收边界条件,模型参数见表2。为了方便观察地震波在各层之内的传播特征,分别在X方向1500m,Y方向1700m,Z方向900m截取快照剖面,图3b到图3d 分别为1000ms时刻3个分量的波场快照。快照图中,各个界面波场特征明显,可以看到第一层海水中只存在纵波没有横波,而且在vx分量的波场快照中,X方向1500m(经过震源)剖面上没有波场传播,这也验证了各向同性介质中纵波源激发不会产生SH波的传播。图3中①代表第一界面产生的反射纵波;②代表第一界面的折射纵波;③代表直达波;④代表第一界面的透射横波;⑤代表第一界面的透射纵波;⑥代表第一界面的透射纵波在第二界面产生的透射纵波;⑦代表第一界面的透射纵波在第二界面产生的反射横波;⑧代表第一界面的透射纵波在第二界面产生的透射横波;⑨代表第一界面的透射纵波在第二界面产生的反射纵波;代表第一界面的透射纵波在第二界面产生的反射纵波,又入射到第一界面产生反射纵波;代表第一界面的透射横波在第二界面产生的反射纵波;代表第一界面的透射横波在第二界面产生的反射横波;代表第一界面的透射横波在第二界面产生的透射横波;代表第一界面的透射横波在第二界面产生的透射纵波。

图3 1000ms时刻的波场快照a 三维层状模型; b vx分量; c vy分量; d vz分量

vP/(m·s-1)vS/(m·s-1)h/m第1层15000750第2层200011541350第3层30001732
并行计算过程中,分析不同进程数以及不同进程分配方案的并行效率,通常是由加速比S来定义:
(6)
其中,WS为计算过程中的串行所用时间;WP为计算过程中的并行所用时间,包括并行计算时间和通信时间;P为计算所用的总进程个数。表3给出了不同计算进程的并行效率。
根据交错网格有限差分格式,在计算速度分量的过程中,X方向需要交换的应力分量为σxx,σxy和σxz;Y方向需要交换的应力分量为σyy,σxy和σyz;Z方向需要交换的应力分量为σzz,σxz和σyz。在计算应力分量的过程中,X,Y,Z方向需要交换的速度分量均为vx,vy,vz。因此每个方向与相邻节点都需要交换3个变量,同时结合交错网格有限差分的空间差分精度N,则该模型正演过程中各个试验单个计算节点与周围相邻的节点需要交换的最多数据量为(单位为3N):当PxPyPz=2×1×1,单个进程数据交换量为480×360=172800;当PxPyPz=2×2×1,单个进程数据交换量为300×360+240×360=194400;当PxPyPz=2×2×2,单个进程数据交换量为300×240+300×180+240×180=169200;当PxPyPz=5×3×2,单个进程数据交换量为120×160+(120×180+160×180)×2=120000。
各个不同试验的计算结果如表3所示,从表3可以看出:①随着计算进程的增加,每个进程分配的计算网格点数减少,单个进程占用内存减少。②随着计算进程的增加,正演计算时间明显减少,同时加速比随着进程数的增加而增加。但是由于串行部分的存在以及交换进程数的增加带来通信时间上的增加,故加速比增加,速度逐渐变小。③单个方向上并行,满足每个进程的交换进程最少(最多为2个);3个方向上并行,满足每个进程的交换信息数最少。
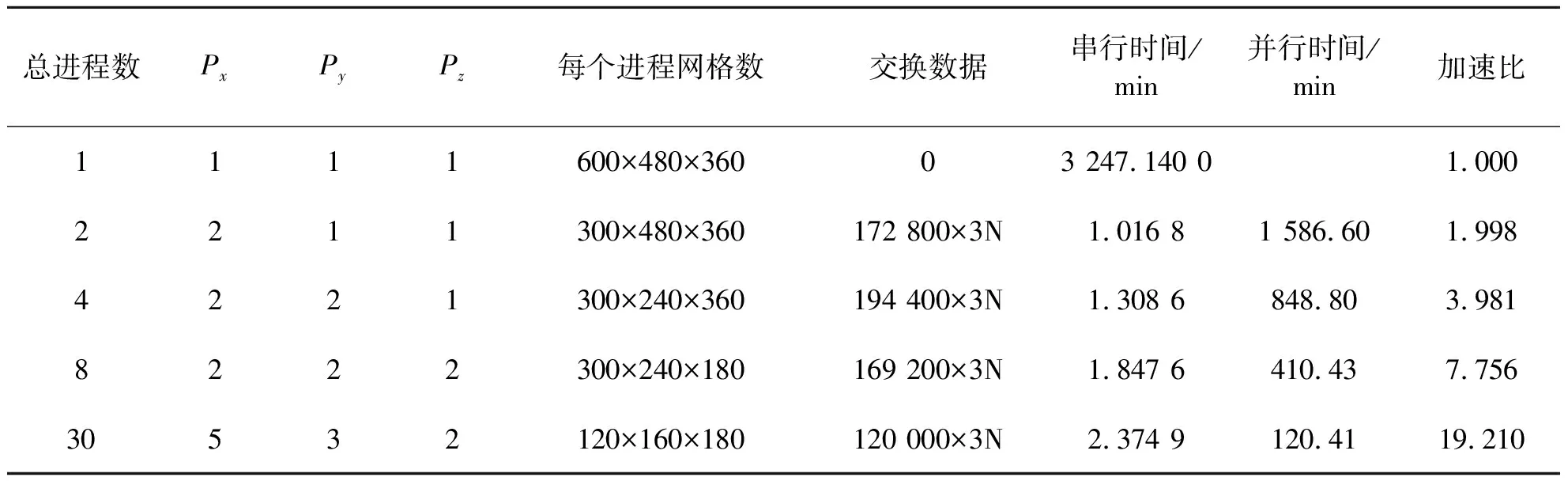
表3 不同计算进程的并行效率
3 海上某靶区OBC三维多波多分量地震观测的数值模拟试验
实际海上某靶区三维地质模型如图4所示,大小为4.5km×10.0km×6.6km。采集所用观测系统如图5所示,一共有8条电缆接收,每条电缆长度为7200m,有240道接收,道间距为30m,缆间距为400m,选取中间的一个震源点来激发。正演过程中空间网格大小为10m×10m×10m,时间步长为0.9ms,记录长度为6s,为了提高正演精度,采用空间8阶有限差分算子进行正演模拟。将正演任务分为60个进程并行计算,其中X,Y,Z方向分别采用的计算进程个数为Px=3,Py=5,Pz=4,正演所用时间为19.8h。图6到图9 为正演得到的多波多分量(4C)记录。图中直达波、折射波、转换横波以及深层海底反射波均能看到。由于接收点位置与震源位置有一定的距离,因此折射波先于直达波到达,尤其是在离震源位置较远的电缆上这种情况更加明显。除了获得了海上4C分量模拟地震数据之外,同时还基于散度和旋度对弹性波场进行分离,得到了分离后的纵波和转换横波记录,如图10到图11所示。可以看出,OBC采集不仅能够接收纵波,还能接收到转换横波,分离后的纵波分量和水听器分量记录大致相同,说明了波场分离的正确性。
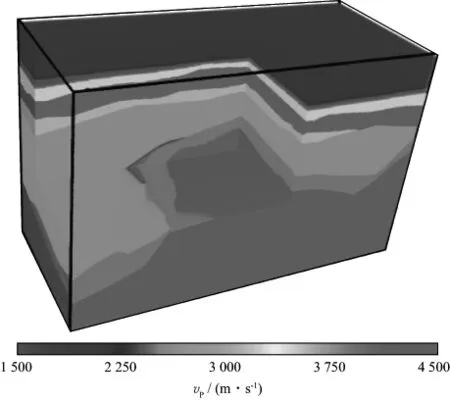
图4 海上某靶区三维地质模型
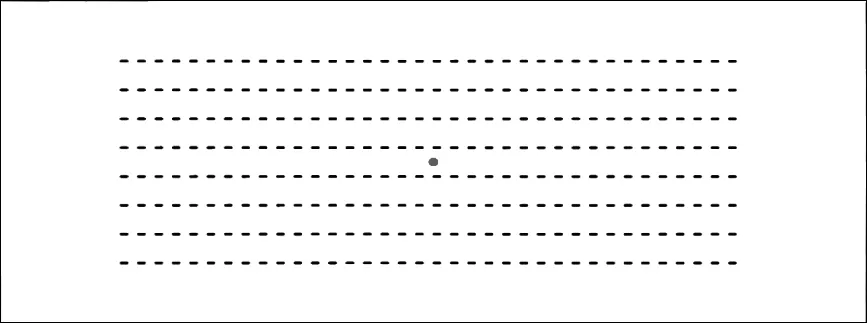
图5 海上某靶区OBC地震采集观测系统(红色为震源)
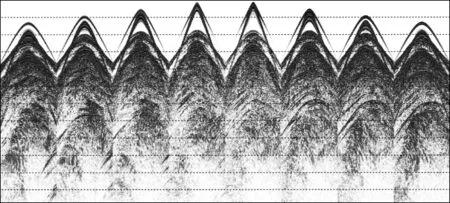
图6 海上某靶区OBC多波多分量(4C)模拟地震记录vx分量
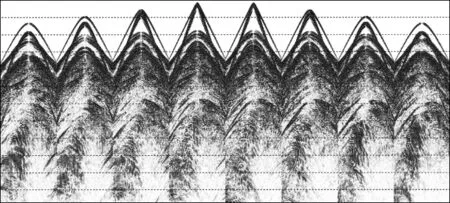
图7 海上某靶区OBC多波多分量(4C)模拟地震记录vy分量
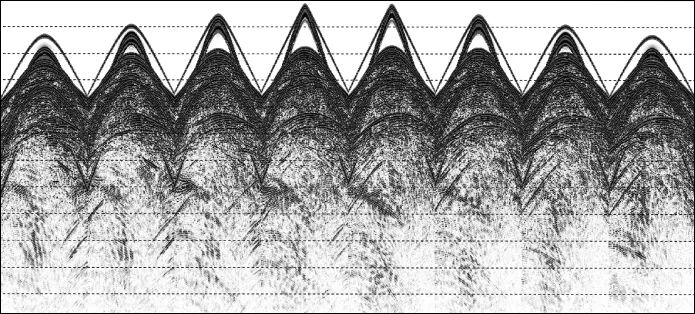
图8 海上某靶区OBC多波多分量(4C)模拟地震记录vz分量
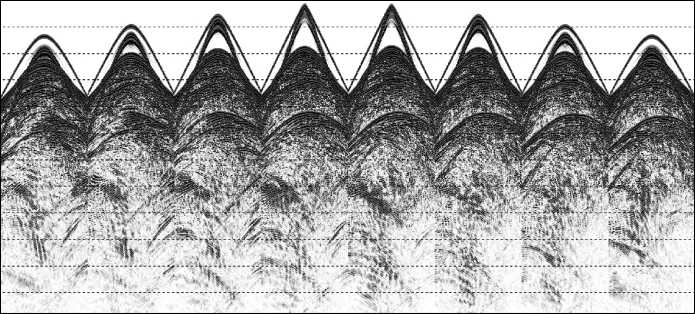
图9 海上某靶区OBC多波多分量(4C)模拟地震记录水听器分量
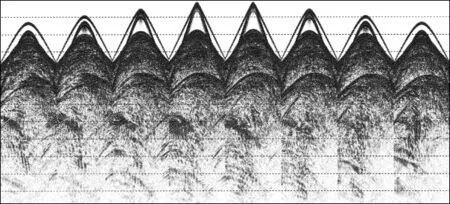
图10 海上某靶区OBC模拟资料波场分离后的纵波分量
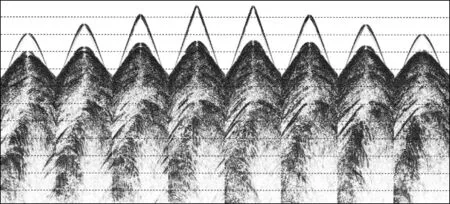
图11 海上某靶区OBC模拟资料波场分离后的横波分量
4 结束语
交错网格有限差分格式具有良好的局部性,非常有利于并行计算。基于MPI的弹性波有限差分正演模拟,将海量三维计算所需内存分配到不同的进程上,减少了各个进程的内存需求,而且每个进程计算三维模型的一部分区域,各个区域并行计算。从X,Y,Z 3个方向将并行任务划分,选择更加灵活,能够合理利用多个计算节点,提高了正演模拟效率。基于MPI的海上多波多分量地震观测的正演模拟可以为研究海上宽方位采集、观测系统论证以及高分辨率成像提供基础数据。
参 考 文 献
[1]CaldwellJ.Marinemulticomponentseismology[J].TheLeadingEdge,1999,18(11):1274-1282
[2] 张树林,夏斌,何家雄.海上多波多分量地震采集技术的应用[J].天然气地球科学,2005,16(1):103-107
ZhangSL,XiaB,HeJX.Theoffshoremulti-wavesandmulti-componentsseismicacquisitiontechnique:acasestudyofYinggehaiBasin[J].NaturalGasGeoscience,2005,16(1):103-107
[3] 张树林,李绪宣,姜立红.海上多波多分量地震技术新进展与发展方向[J].物探化探计算技术,2000,22(2):97-107
ZhangSL,LiXX,JiangLH.ImprovementanddevelopmentofChinaoffshoremultiwaveandmulticomponentseismictechnique[J].ComputingTechniquesforGeophysicalandGeochemicalExploration,2000,22(2):97-107
[4] 刘海波,全海燕,陈浩林,等.海上多波多分量地震采集综述[J].中国石油勘探,2007,12(3):52-57
LiuHB,QuanHY,ChenHL,etal.Overviewofmarinemulti-waveandmulti-componentseismicacquisition[J].ChinaPetroleumExploration,2007,12(3):52-57
[5]HeHY,ZhouHZ,FuDD.Multicomponentseismic-explorationinYinggehaiBasin[J].TheLeadingEdge,2002,21(9):914-920
[6]VirieuxJ.SHwavepropagationinheterogenousmedia:velocity-stressfinite-differencemethod[J].Geophysics,1984,49(11):1933-1957
[7]VirieuxJ.P-SVwavepropagationinheterogenousmedia:velocity-stressfinite-differencemethod[J].Geophysics,1986,51(4):889-901
[8]LevanderAR.Fourth-orderfinite-differenceP-SVseismograms[J].Geophysics,1988,53(11):1425-1436
[9] 董良国,马在田,曹景忠,等.一阶弹性波方程交错网格高阶差分解法[J].地球物理学报,2000,43(3):411-419
DongLG,MaZT,CaoJZ,etal.Astaggered-gridhigh-orderdifferencemethodofone-orderelasticwaveequation[J].ChineseJournalofGeophysics,2000,43(3):411-419
[10] 裴正林.三维各向同性介质弹性波方程交错网格高阶有限差分模拟[J].石油物探,2005,44(4):308-315
PeiZL.Numericalsimulationofelasticwaveequationin3-Disotropicmediawithstaggered-gridhigh-orderdifferencemethod[J].GeophysicalProspectingforPetroleum,2005,44(4):308-315
[11] 裴正林.三维各向异性介质中弹性波方程交错网格高阶有限差分法数值模拟[J].石油大学学报(自然科学版),2004,28(5):23-29
PeiZL.Three-dimensionalnumericalsimulationofelasticwavepropagationin3-Danisotropicmediawithstaggered-gridhigh-orderdifferencemethod[J].JournaloftheUniversityofPetroleum,China,2004,28(5):23-29
[12] 张军华,臧胜涛,单联瑜,等.高性能计算的发展现状及趋势[J].石油地球物理勘探,2010,45(6):918-925
ZhangJH,ZangST,ShanLY,etal.Developmentstatusandtrendsforhighperformancecomputing[J].OilGeophysicalProspectingforPetroleum,2010,45(6):918-925
[13] 都志辉.高性能计算并行编程技术—MPI并行程序设计[M].北京:清华大学出版社,2001:13-15
YuZH.Parallelprogramtechniqueofhighperformancecomputation—MPIparallelprogramdesign[M].Beijing:TsinghuaUniversityPress,2001:13-15
[14]FurumuraT,KoketsuK,WenKL.ParallelPSM/FDMhybridsimulationofgroundmotionsfromthe1999Chi-chi,Taiwan,earthquake[J].PureandAppliedGeophysics,2002,159(9):2133-2146
[15]BohlenT.Parallel3-Dviscoelasticfinitedifferenceseismicmodeling[J].Computers&Geosciences,2002,28(8):887-899
[16]MicikeviciusP.3DfinitedifferencecomputationonGPUsusingCUDA[J].ExpandedAbstractsof2ndWorkshoponGeneralPurposeProcessingonGraphicsProcessingUnits,2009,79-84
[17] 王德利,雍运动,韩立国,等.三维粘弹介质地震波场有限差分并行模拟[J].西北地震学报,2007,29(1):30-34
WangDL,YongYD,HanLG,etal.Parallelsimulationoffinitedifferenceforseismicwavefiledmodelingin3-Dviscoelasticmedia[J].NorthwesternSeismologicalJournal,2007,29(1):30-34
[18] 王月英.基于MPI的三维波动方程有限元法并行正演模拟[J].石油物探,2009,48(3):221-243
WangYY.3Dwave-equationfinite-elementforwardmodelingbasedonmessagepassinginterfaceparallelcomputing[J].GeophysicalProspectingforPetroleum,2009,48(3):221-243
[19] 何兵寿,张会星,韩令贺.弹性波方程正演的粗粒度并行算法[J].地球物理学进展,2010,25(2):650-656
HeBS,ZhangHX,HanLH.Forwardmodelingofelasticwaveequationwithcoarse-grainedalgorithem[J].ProgressinGeophysic,2010,25(2):650-656
[20] 魏星,王彦宾,陈晓非.模拟地震波场的伪谱和高阶有限差分混合方法[J].地震学报,2010,32(4):392-400
WeiX,WangYB,ChenXF.HybridPSM/FDMmethodforseismicwavefieldsimulation[J].ActaSeismologicaSinica,2010,32(4):392-400
[21] 秦艳芳,王彦宾.地震波传播的三维伪谱和高阶有限差分混合方法并行模拟[J].地震学报,2012,34(2):147-156
QinYF,WangYB.Three-dimensionalparallelhybridPSM/FDMsimulationofseismicwavepropagation[J].ActaSeismologicaSinica,2012,34(2):147-156
[22] 公续飞,杜启振.三维弹性波有限差分数值模拟及其GPU并行实现[C]∥中国地球物理学会第二十七届年会论文集.长沙:中国地球物理学会,2011:485
GongXF,DuQZ.Finite-differencesimulationof3DelasticwavefieldanditsimplementationonGPU[C]∥ChineseGeophysicalSociety27thAnnualMeetingProceeding.Changsha:ChineseGeophysicalSociety,2011:485
[23] 段玉婷,李靖宇,胡天悦.基于GPU的三维精细积分法正演模拟[C]∥中国地球物理学会第二十七届年会论文集.长沙:中国地球物理学会,2011:484
DuanYT,LiJY,HuTY.Applicationofthe3DpreciseintegrationmethodforseismicmodelingbasedonGPU[C]∥ChineseGeophysicalSociety27thAnnualMeetingProceeding.Changsha:ChineseGeophysicalSociety,2011:484
[24] 张明财,熊章强,张大洲.基于MPI的三维瑞雷面波有限差分并行模拟[J].石油物探,2013,52(4):354-362
ZhangMC,XiongZQ,ZhangDZ.3DfinitedifferenceparallelsimulationofRayleighwavebasedonmessagepassinginterface[J].GeophysicalProspectingforPetroleum,2005,44(4):308-315
[25] 牟永光,裴正林.三维复杂介质地震数值模拟[M].北京:石油工业出版社,2005:16-18
MouYG,PeiZL.Seismicnumericalmodelingfor3-Dcomplexmedia[M].Beijing:PetroleumIndustryPress,2005:16-18

