裂缝型储层预测的稳定方位AVO梯度无约束反演方法研究
印兴耀,刘志国,李春鹏,,李爱山,盖海洋
(1.中国石油大学(华东)地球科学与技术学院,山东青岛266580;2.中海油研究总院,北京100028)
裂缝作为地壳中一种普遍的构造现象,广泛存在于各类岩石中。到目前为止,已在砂岩、泥页岩和碳酸盐岩,甚至火成岩等各类岩石的裂缝型储层中获得了大量的工业油气流。地震波在裂缝型地层中传播会发生横波分裂现象,Ata等[1]指出快横波极化方向平行于裂缝走向,慢横波极化方向垂直于裂缝走向,为利用横波技术进行裂缝勘探奠定了理论基础。但是实际横波地震勘探成本非常昂贵,因此需要发展成本相对比较低廉的裂缝型地层纵波勘探技术。裂缝型地层具有较强的纵波方位各向异性,梁锴[2]和思芗等[3]分别推导了二维和三维情况下TI介质反射透射方程;Grechka等[4]研究了方位AVO梯度与裂缝参数之间的关系;刘洋等[5]、范国章等[6]讨论了裂缝倾角与AVO随方位变化的关系,倾角越小,AVO方位变化特征也越小;Liu等[7]研究了薄裂缝层的方位AVO特征,当薄层厚度大于1/4地震波长时可以得到准确的裂缝密度和走向;Gray等[8]认为方位AVO的各向异性程度与裂缝开启、流体填充和裂缝倾角等因素有关。因此,通过方位纵波地震数据提取地层方位AVO梯度识别地层裂缝的方法是切实可行的。
常规方位AVO梯度提取方法对各个方位地震道集独立进行,该方法提取的AVO截距项即自激自收反射系数在各个方位可能会不一致,进而会影响方位AVO梯度的精度。虽然方位AVO梯度反演方法可以将截距项和各方位梯度项同时引入反演方程,得到截距项一致的方位AVO梯度,但该方法需要各向异性先验信息以稳定反演结果。为了克服常规方位AVO梯度提取方法截距项难以一致和方位AVO梯度反演方法所需各向异性测井信息匮乏的问题,我们发展了稳定的方位AVO梯度无约束反演方法。据此研究了截距项一致情况下4类含气砂岩方位AVO梯度与裂缝参数之间的关系,并且通过模型试算和实际工区应用验证了该反演方法的有效性,为裂缝型储层预测提供了有利的技术支撑。
1 方位AVO梯度与裂缝参数
近垂直定向分布的裂缝型地层具有方位各向异性特征,它导致AVO梯度随着方位变化而变化。因此,有必要研究方位AVO截距项一致情况下,方位AVO梯度与地层裂缝参数之间的关系,为利用方位AVO梯度预测裂缝密度和裂缝走向提供理论基础。
1.1 方位AVO梯度与裂缝密度
Rutherford等[9]和Castagna等[10]描述了4类含气砂岩的AVO特征,这4类含气砂岩模型的纵波速度、横波速度和密度如表1所示。假设这4类含气砂岩是由石英、孔隙和气体构成的,根据《岩石物理手册》[11],相关弹性参数见表2。
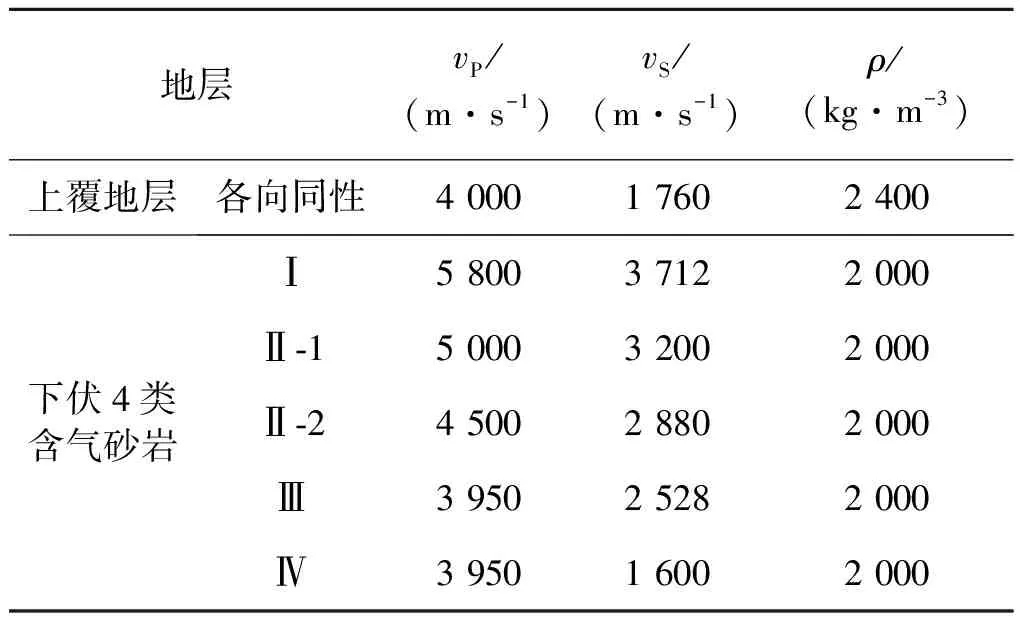
表1 4类含气砂岩弹性参数
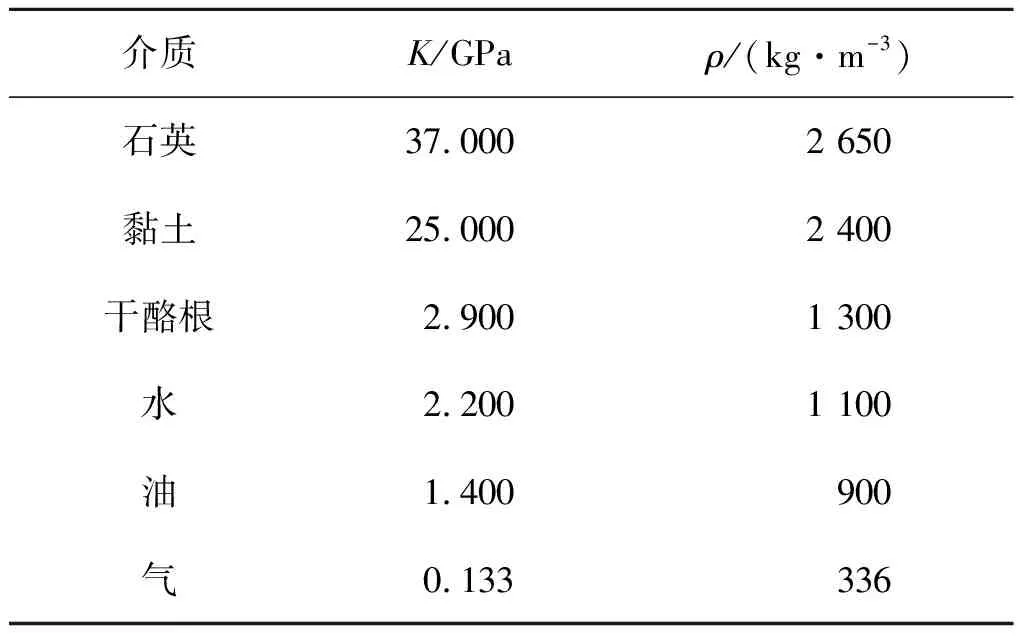
表2 常见矿物弹性参数
在以上4类含气砂岩中嵌入近垂直定向分布的裂缝,裂缝密度e分别为0.05,0.10,0.15,裂缝纵横比为0.01,裂缝走向为90°。根据李春鹏等[12]推导的HTI介质弹性波反射透射方程计算4类含气砂岩模型的方位反射系数,并且将反演的方位AVO梯度拟合成椭圆,以研究方位AVO梯度与裂缝密度之间的关系。
图1至图5显示了4类含气砂岩裂缝密度e分别为0.05,0.10,0.15时的方位AVO梯度和椭圆拟合结果,图中方位AVO梯度近似为一条周期为π的余弦曲线,且裂缝走向与裂缝倾向的方位AVO梯度差异最大;裂缝密度越大,第Ⅰ,Ⅱ-1,Ⅱ-2和Ⅲ类含气砂岩裂缝走向与裂缝倾向的方位AVO梯度差异也越大,但是第Ⅳ类含气砂岩的差异却先增大后减小。
方位AVO梯度可以拟合成椭圆,表3显示了4类含气砂岩裂缝密度e分别为0.05,0.10,0.15时的椭圆率,椭圆率=(椭圆长轴-椭圆短轴)/椭圆长轴。表3中裂缝密度越大,第Ⅰ,Ⅱ-1,Ⅱ-2和Ⅲ类含气砂岩椭圆率也越大,但是第Ⅳ类含气砂岩的椭圆率先增大后减小。大体来说,裂缝密度越大相应的方位AVO梯度椭圆率也越大,据此可以用于实际工区裂缝密度预测研究。
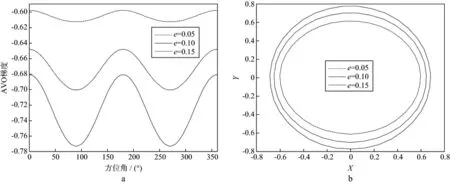
图1 第Ⅰ类含气砂岩裂缝密度e分别为0.05,0.10,0.15时的方位AVO梯度(a)和方位AVO梯度的椭圆拟合结果(b)
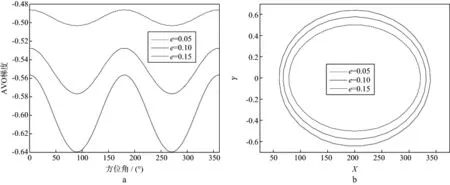
图2 第Ⅱ -1类含气砂岩裂缝密度e分别为0.05,0.10,0.15时的方位AVO梯度(a)和方位AVO梯度的椭圆拟合结果(b)
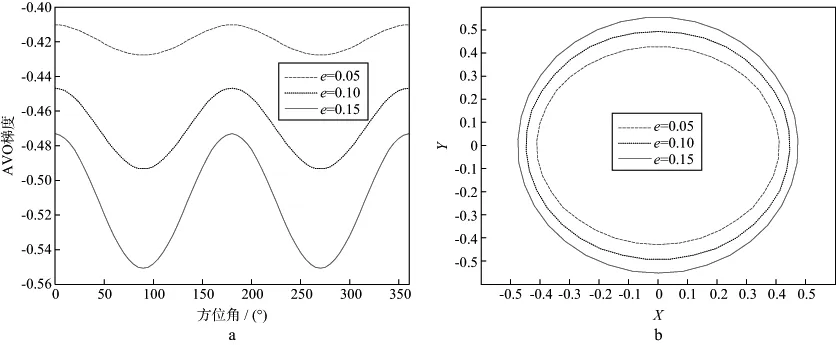
图3 第Ⅱ -2类含气砂岩裂缝密度e分别为0.05,0.10,0.15时的方位AVO梯度(a)和方位AVO梯度的椭圆拟合结果(b)
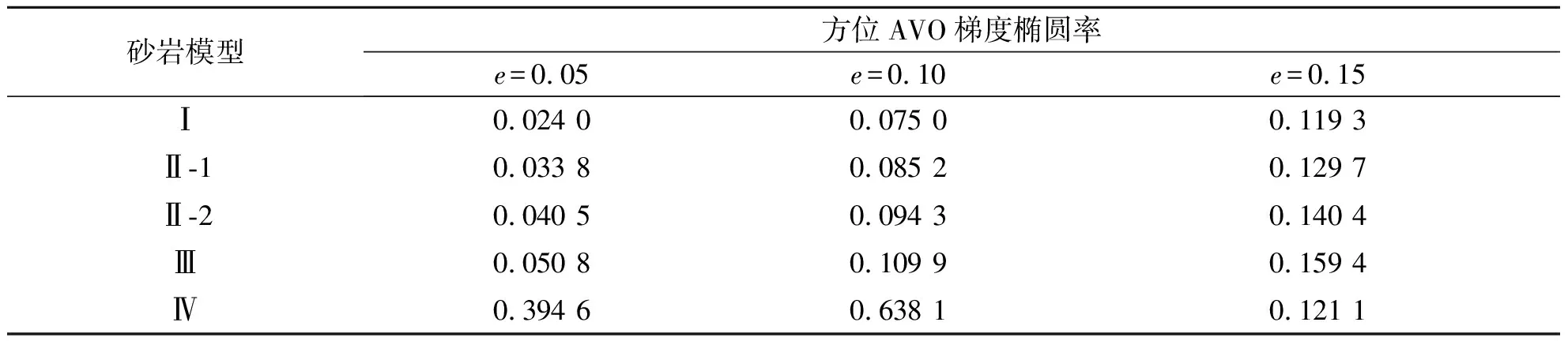
砂岩模型方位AVO梯度椭圆率e=0.05e=0.10e=0.15Ⅰ0.02400.07500.1193Ⅱ-10.03380.08520.1297Ⅱ-20.04050.09430.1404Ⅲ0.05080.10990.1594Ⅳ0.39460.63810.1211
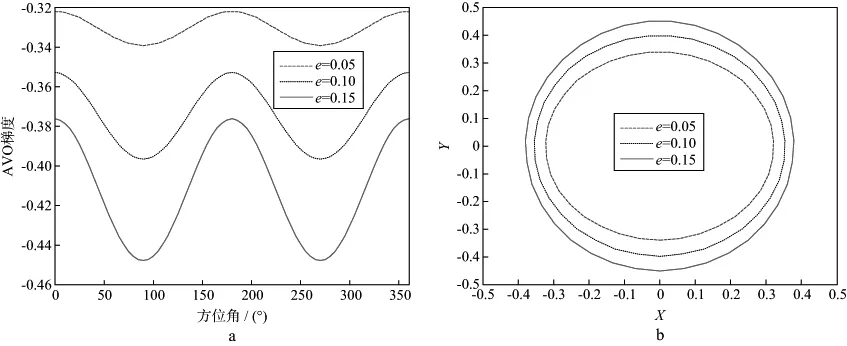
图4 第Ⅲ类含气砂岩裂缝密度e分别为0.05,0.10,0.15时的方位AVO梯度(a)和方位AVO梯度的椭圆拟合结果(b)

图5 第Ⅳ类含气砂岩裂缝密度e分别为0.05,0.10,0.15时的方位AVO梯度(a)和方位AVO梯度的椭圆拟合结果(b)
1.2 方位AVO梯度与裂缝走向
上述第Ⅳ类含气砂岩的第1层为均匀各向同性介质,第2层为裂缝介质,裂缝密度是0.05,裂缝纵横比为0.005,裂缝走向为90°,假设第2层裂缝介质之下有一个均匀各向同性介质且弹性参数与第1层相同。通过模型试算研究方位AVO梯度椭圆半轴方向与裂缝走向之间的关系。图6a显示了第Ⅳ类含气砂岩顶、底界面的方位AVO梯度,图中顶、底界面的方位AVO梯度呈反相关关系,顶界面裂缝走向处的AVO梯度最大,底界面裂缝走向处的AVO梯度最小。图6b显示了第Ⅳ类含气砂岩顶、底界面方位AVO梯度椭圆拟合结果,图中顶界面椭圆长轴指示裂缝走向,底界面椭圆短轴指示裂缝走向。因此,方位AVO梯度椭圆半轴可以指示裂缝走向,但是却存在90°不确定性。
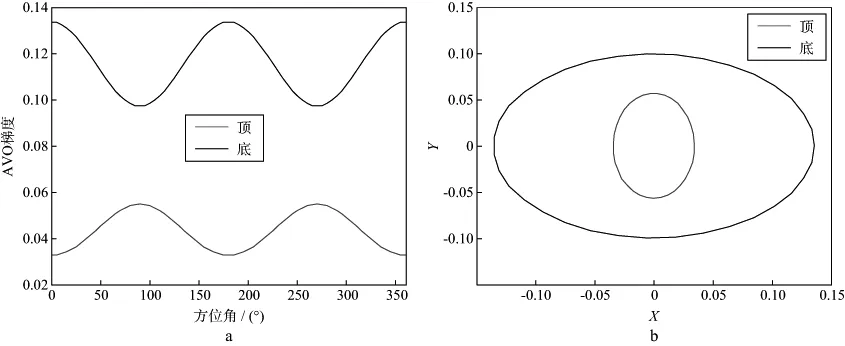
图6 第Ⅳ类含气砂岩顶、底界面方位AVO梯度(a)和方位AVO梯度椭圆拟合结果(b)
2 稳定方位AVO梯度反演方法
常规方位AVO梯度提取方法是在各个方位独立进行的,该方法提取的AVO截距项即自激自收反射系数在各个方位可能会不一致,进一步会影响方位AVO梯度的精度。为了克服各个方位AVO截距不一致的问题和实际工区各向异性测井信息匮乏的问题,我们发展了稳定的方位AVO梯度无约束反演方法。
2.1 假设方位地震数据是方位反射系数
入射角小于30°时,方位反射系数公式为
(1)
式中:R表示方位反射系数;A表示AVO截距;B表示方位AVO梯度;φ表示方位角;θ表示入射角。地震数据S的正演方程为
(2)
式中:W表示子波矩阵;R表示方位反射系数序列;G表示反射系数正演算子矩阵;m=[AB1B2…BN]T表示待反演参数,其中,B1,B2,…,BN表示各个方位的AVO梯度序列,N表示方位角数目。
假设方位地震数据是方位反射系数,则方位地震数据的正演方程为
(3)

(2)式的最小二乘反演方程为
(4)
(3)式的最小二乘反演方程为
(5)
(5)式相对于(4)式消除了地震子波的影响,增强了反演方程的稳定性。
2.2 最少反射层假设降低反褶积维度
通过地震反褶积将上述得到的方位AVO梯度地震数据体wB1,wB2,…,wBN转换为方位AVO梯度数据体B1,B2,…,BN,然后通过椭圆拟合得到方位AVO梯度椭圆率和椭圆半轴方向。但是,常规反褶积方法得到的反射系数不是稀疏的,不能真正反映地下地层界面的真实情况。我们采取Perez等[13]提出的最少反射层地震反演方法,搜索准确的地下界面位置,以降低方位AVO梯度地震记录反褶积方程维数和条件数,得到稳定的反演结果。该方法假设地下地层是稀疏分布的,通过降低小子波矩阵w维数和反褶积系数矩阵wTw条件数,以获得稳定的反演结果。最少反射层稀疏脉冲反演的关键性技术是模拟退火法寻找反射层位置和线性优化方法解目标函数[14-16]。假设单道采样点数为L,采样率为dt。模拟退火法实现步骤如下。
1) 给定反射层个数M,反射层位置τj范围[0,L·dt],子波主频f范围[fmin,fmax]和初始相位φ范围[φmin,φmax];给定初始温度T0,回火升温次数Nb,每次降温迭代次数Nt,收敛阈值ε,子波尺度因子s,子波时间长度tw。转到步骤2)。
2) 令i=1,b=0,T=T0,随机给定τj,f和φ初始值。
(6)
式中:i0是地震道下标矢量;floor(·)是四舍五入函数;frand(·)是均匀分布随机函数;fsort(·)是从小到大排序函数。转到步骤3)。

4) 接受方式。
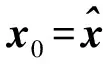
5) 降温方式。
T=T0e-C(i-1),其中,C是降温因子,C越小降温越慢。转到步骤6)。
6) 模型位置扰动。
令i=i+1。
如果i>Nt,则i=1,b=b+1;
此法是在显微镜下直接进行测定,方便快捷并且仪器损耗较小,但在一定的容积中微生物的个体数目包括死活细胞均被计算在内,还有微小杂物也被计算在内,这样得出结果往往偏高,因此适用于对形态个体较大的菌体计数。
如果b>Nb,转到步骤8);
如果b≡0,则
(7)
否则
(8)
式中:fsign(·)是符号函数;funidrnd(M,1)表示从1到M随机找一个整数。转到步骤7)。
7) 子波扰动。
τj(τj<0‖τj>L·dt)=frand·L·dt
τj=fsort(τj)

f(f
(fmax-fmin)

fsign(frand-0.5)·(φmax-φmin)
φ(φ<φmin‖φ>φmax)=φmin+frand·
(φmax-φmin)
(9)
其中,λ是扰动因子,λ越大扰动时间越长,转到步骤3)。
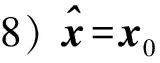
3 模型试算
为了验证稳定方位AVO梯度反演方法的有效性,设计4层三维模型如图7所示,第1层、第2层和第4层是各向同性介质,其中第1层介质的纵波速度、横波速度、密度和厚度分别为2500m/s,1500m/s,2000kg/m3和20m,第2层介质的纵波速度、横波速度、密度和厚度分别是3000m/s,1800m/s,2300kg/m3和80m,第4层介质的纵波速度、横波速度和密度分别是3200m/s,1850m/s,2350kg/m3。第3层介质是80m厚的近垂直定向分布的裂缝介质,该裂缝介质的背景弹性参数和物性参数取自于某油田A井的测井信息,其中A井S地层的纵波速度、横波速度、密度、石英含量、泥质含量和干酪根含量的均值分别是3476m/s,1935m/s,2400kg/m3,11.28760,17.58680和5.24508。假设该模型inline和xline方向各有100条测线,图8给出了第3层裂缝介质的裂缝密度平面分布、裂缝走向平面分布和裂缝走向玫瑰图。
根据李春鹏等[12]推导的HTI介质弹性波反射透射方程可以计算该模型的方位纵波反射系数。模型正演采用相移30°后的50Hz雷克子波,入射角分别是15°,25°和35°,方位角分别是0,30°,60°,90°,120°,150°,180°。图9显示了inline75,xline50处,入射角为35°,信噪比为10,采样间隔为1ms的方位纵波地震记录,图中第15采样点左右处的同相轴表示模型第1层和第2层的各向同性界面的方位地震记录,各向同性界面的地震记录与方位角无关;图中第70和第150采样点左右处的同相轴分别表示第3层裂缝介质顶面和底面的方位地震记录,裂缝介质顶面和底面的地震记录随方位角变化而变化。
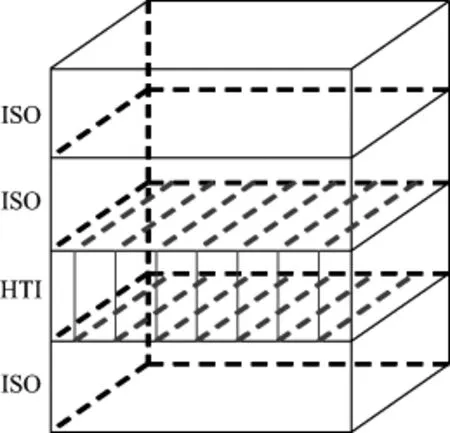
图7 4层介质模型示意图解

图8 4层介质模型的第3层裂缝介质参数a 裂缝密度平面分布; b 裂缝走向平面分布(黑色小线段长度指示裂缝密度大小,小线段方向指示裂缝走向); c 裂缝走向玫瑰图
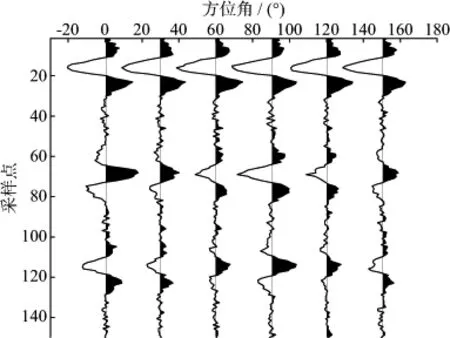
图9 4层介质模型inline75,xline50处,入射角为35°,信噪比为10的方位地震记录
稳定方位AVO梯度反演可以分为两步。
第一步:假设方位地震数据是方位反射系数,根据(5)式的反演方程,4层介质模型的反演矩阵GTG条件数约为527,但若采用(4)式的反演方程,4层介质模型的反演矩阵(WG)T(WG)条件数约为7.3×1017,可见(5)式的反演方程稳定性相对较高。4层介质模型的inline75,xline50处反演结果见图10a和图10b,图中反演的AVO截距地震记录和实际自激自收反射地震记录吻合得较好,并且各向同性界面的AVO梯度地震记录基本与方位无关,但第3层裂缝地层顶、底的AVO梯度地震记录随方位变化,说明反演结果能够指示地层裂缝发育情况。
第二步:方位AVO梯度地震数据体wB1,wB2,…,wBN转换为方位AVO梯度数据体B1,B2,…,BN,但是反褶积算子wTw的条件数约为1.6×1018,一般采用正则化算法改善反褶积算子,但是这种常规反褶积方法得到的反射系数不是稀疏的,不能真正地反映下地层界面的真实情况。我们采用最少反射层假设反演C和D数据体,假设4层介质模型有6个地层分界面,inline75,xline50处反演结果见图10c,图中各向同性界面的AVO梯度基本与方位无关,但裂缝地层顶、底的AVO梯度随方位变化,说明反演结果能够指示地层裂缝发育情况。其余地层分界面处几乎为0,说明最少反射层假设方法不仅能搜索真实地层界面,而且在非裂缝地层分界面处得到的值几乎为0。
对4层介质模型基于稳定方位AVO梯度反演方法得到的结果进行方位AVO梯度椭圆分析(图11)。比较图11a和图8a可以发现,方位AVO梯度椭圆率基本可以反映裂缝地层裂缝密度的平面展布;比较图11b和图8b可以发现,方位AVO梯度椭圆半轴方向与裂缝地层裂缝走向基本一致或垂直;图11c中方位AVO梯度椭圆半轴主方向与裂缝走向主方向一致。由此可见,稳定方位AVO梯度反演方法得到的方位AVO梯度椭圆率可以指示裂缝密度,方位AVO梯度椭圆半轴方向可以指示裂缝走向。
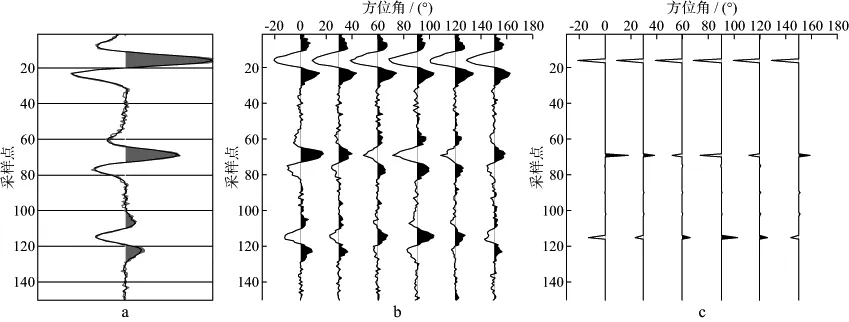
图10 4层介质模型inline75,xline50处的稳定方位AVO梯度反演结果a 第一步反演AVO截距地震记录(黑)与真实自激自收地震记录(红)对比; b 第一步反演的方位AVO梯度地震记录; c 第二步反演的方位AVO梯度
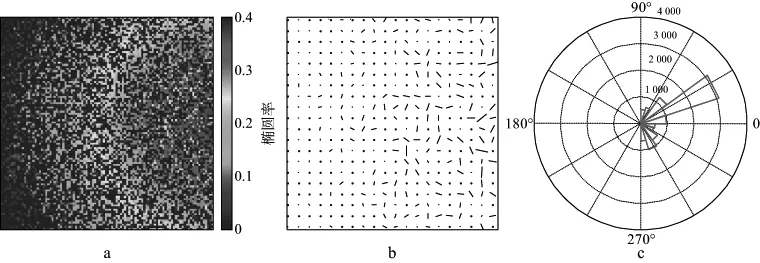
图11 4层介质模型稳定方位AVO梯度反演结果的方位AVO梯度椭圆分析a 椭圆率平面分布; b 椭圆半轴方向平面分布(黑色小线段长度指示裂缝密度大小,小线段方向指示裂缝走向); c 椭圆半轴方向玫瑰图
4 实际裂缝地层预测应用
某油田发育大段泥页岩裂缝地层,工区内地震、测井资料比较完备,特别是裂缝比较发育的S地层叠后道集上存在着明显的方位变化,适合于利用地震方位道集数据进行裂缝型储层预测研究。对该油田三维宽方位观测系统的所有可能的炮检-方位角分析可知,所观测地震数据随炮检距和方位角的分布比较均匀,只是在大炮检距的小方位角和大方位角数据有点缺失。通过地震资料处理,得到分别为0~30°,30°~60°,60°~90°,90°~120°,120°~150°,150°~180°的6个方位叠加资料。利用稳定方位AVO梯度反演方法预测S地层的裂缝密度、走向和发育带,图12给出了预测分析结果。图12中A井附近存在方位AVO梯度异常,稳定方位AVO梯度反演结果的方位AVO梯度方向与测井解释结果一致,但存在90°不确定性。

图12 某油田S地层稳定方位AVO梯度反演裂缝预测结果与测井解释结果a 各向异性梯度; b 各向异性梯度方向玫瑰图; c A井测井解释结果
5 结束语
针对常规方位AVO梯度提取方法各个方位AVO截距不一致的问题和实际工区各向异性测井信息匮乏的问题,我们研究了方位AVO截距项一致情况下方位AVO梯度与裂缝参数之间的关系,提出了稳定方位AVO梯度无约束反演方法,得到以下3点认识。
1) 4类含气砂岩的岩石物理模型正演研究结果表明,方位AVO梯度椭圆率能够指示裂缝发育区;椭圆半轴方向可以指示裂缝走向,但是存在90°不确定性。
2) 稳定方位AVO梯度无约束反演方法能够提高方位AVO梯度反演方程稳定性,并能得到准确的地下地层方位AVO梯度信息。
3) 实际工区应用结果表明,利用稳定方位AVO梯度无约束反演方法得到的方位AVO梯度可以较为准确地预测地层裂缝发育带,为裂缝型储层预测提供了有利的技术支撑。
参 考 文 献
[1] Ata E B,Michelena R J.Mapping distribution of fractures in a reservoir with P-S converted waves[J].The Leading Edge,1995,14(6):664-674
[2] 梁锴.TI介质地震波传播特征与正演方法研究[D].山东:中国石油大学(华东),2009
Liang K.The study on propagation feature and forward modeling of seismic wave in TI media[D].Shandong:China University of Petroleum,1996
[3] 司芗,吴国忱.裂隙等效TTI介质qP波反射特征研究[J].地球物理学进展,2012,27(5):2091-2099
Si X,Wu G C.Study on qP-wave reflectivity in fracture equivalent TTI media[J].Progress in Geophysics (in Chinese),2012,27(5):2091-2099
[4] Grechka V,Tsvankin I.NMO-velocity surfaces and Dix-type formulas in anisotropic heterogeneous media[J].Geophysics,2002,67(3):939-951
[5] 刘洋,董敏煜.各向异性介质中的方位AVO[J].石油地球物理勘探,1999,34(3):261-269
Liu Y,Dong M Y.Azimuthal AVO in anisotropic medium[J].Oil Geophysical Prospecting,1999,34(3):261-269
[6] 范国章,牟永光,金之钧.裂缝介质中地震波方位AVO特征分析[J].石油学报,2002,23(4):42-46
Fan G Z,Mou Y G,Jin Z J.Amplitude versus offset characteristic of Azimuth of seismic wave in fractured reservoir[J].Acta Petrolei Sinica,2002,23(4):42-46
[7] Liu Y L,Ziolkowski A,Liu E R,et al.Characterization of azimuthal anisotropy in the presence of thin layers using P-waves[J].Expanded Abstracts of 71stAnnual Internat SEG Mtg,2001,169-172
[8] Gray D,Roberts G,Conoco H K.Recent advances in determination of fracture strike and crack density from P-wave seismic data[J].The Leading Edge,2002,21(3):280-285
[9] Rutherford S R,Williams R H.Amplitude-versus-offset variations in gas sands[J].Geophysics,1989,54(6):680-688
[10] Castagna J P,Swan H W,Foster D J.Framework for AVO gradient and intercept interpretation[J].Geophysics,1998,63(3):948-956
[11] Mavko G,Mukerji T,Dnorikin J.The rock physics handbook:tools for seismic analysis in porous media[M].Cambridge:Cambridge University Press,1998:260-263
[12] 李春鹏,印兴耀,张峰.HTI介质饱和流体特性和裂缝密度对方位反射系数的影响[J].石油物探,2013,52(1):1-10
Li C P,Yin X Y,Zhang F.Influence of HTI medium saturated fluid properties and fracture density on azimuthal reflectivity[J].Geophysical Prospecting for Petroleum,2013,52(1):1-10
[13] Perez O D,Velis R D.Sparse-spike AVO/AVA attributes from prestack data[J].Expanded Abstracts of 81stAnnual Internat SEG Mtg,2011,340-344
[14] 赵改善.用模拟退火法作AVA反演[J].石油物探,1992,31(4):1-10
Zhao G S.AVA inversion by use of simulated annealing[J].Geophysical Prospecting for Petroleum,1992,31(4):1-10
[15] 王振国,陈小宏,王克斌,等.多参数优化的模拟退火法波阻抗反演[J].石油物探,2007,46(2):120-125
Wang Z G,Chen X H,Wang K B,et al.Simulated annealing of multi-parameter optimization method of wave impedance inversion[J].Geophysical Prospecting for Petroleum,2007,46(2):120-125
[16] 李大卫,尹成,谢兵.模拟退火独立分量分析方法及应用[J].石油物探,2007,46(1):24-27
Li D W,Yin C,Xie B.Independent component analysis method and simulated annealing[J].Geophysical Prospecting for Petroleum,2007,46(1):24-27

