大地电磁非线性共轭梯度一维反演
管贻亮,李予国,胡祖志,黄江波,胡祥云
(1.中国地质大学(武汉)地球物理与空间信息学院,湖北武汉430074;2.中国海洋大学海洋地球科学学院,山东青岛266100;3.中国石油集团东方地球物理勘探有限责任公司,河北涿州072751)
大地电磁测深(MT)是以天然交变电磁场为场源,研究地壳和上地幔构造的一种地球物理勘探方法[1]。20世纪50年代初,苏联学者Tikhonov[2]和法国学者Cagniard[3]建立了探测地球深部电性结构的大地电磁测深法。该方法工作简便,勘探深度大,在矿产普查与勘探、地壳与上地幔电性结构研究、地热田的调查以及石油天然气勘探等方面发挥了重要作用[4]。
当前大地电磁测深一维反演常用的反演方法有Bostick近似反演法、高斯-牛顿法、马夸特法[5]、模拟退火法[6]、Occam法[7]等,不同的方法有各自不同的特点[8-9]。在高斯-牛顿算法和Mackie-Madden算法[10-11]的基础上发展起来的非线性共轭梯度法(NLCG)多用于二维反演[12],Newman等[13]将其用于三维反演。它突破了线性化迭代反演的框架,能够直接对非二次极小化问题求解[14]。但是该算法由于计算量较大,正则化因子选取较困难,很少被用于实际资料的一维反演,在一维反演方面的应用研究也很少。
本文结合一维反演实际,提出了非线性共轭梯度一维反演算法的简化和改进方案。
1 大地电磁测深的基本理论
大地电磁测深的场源是天然交变电磁场,其理论基础是卡尼尔-吉洪诺夫理论,将场源近似看成平面波垂直入射大地。当交变电磁场在地下介质中传播时,由于趋肤深度的作用,不同频率的信号具有不同的穿透深度,在地面上观测大地电磁场,它的频率响应能反映地下介质电性的垂向分布情况[15]。为了得到地下介质电阻率的分布信息,引入波阻抗的概念:Z=E/H。
地面波阻抗可依次用其下相邻介质顶面的波阻抗来表示,由于波阻抗在分界面上是连续的,对于层状介质,任一层顶界面的波阻抗等于其上相邻介质底界面的波阻抗,因而问题转变为求解同一层介质顶、底界面波阻抗之间的关系[1]。因为每层介质都是均匀各向同性的,因此顶、底界面的波阻抗可用积分常数联系起来,由此得到大地电磁正演的递推公式
(1)
式中:Z为波阻抗;E为电场强度;ω为圆频率;k为复波数;h为地层厚度;μ为磁导率;ρa为视电阻率。
2 大地电磁数据NLCG一维反演算法

2.1 非线性共轭梯度法原理
Rodi等[12]将NLCG法反演问题表示成
(2)
式中:d为数据矢量;m为模型矢量;F为正演算子;e是残差向量。
按照Tikhonov和Arsenin的正则化方法[16]处理目标函数的最小化问题,定义目标函数Ψ为
(3)

正演函数的雅可比矩阵A为
(4)
目标函数Ψ(m)的梯度向量g和Hessian矩阵H定义为
(5)
式中:B是F的Hessian矩阵;M是模型参数个数;N是地层个数。在非线性共轭梯度算法中,同样首先给定初始模型,通过求解一元极小化问题或者沿着计算的方向进行线性搜索确定模型序列:
(6)
式中:m0为给定的初始模型;pl为搜索方向;al为搜索步长。在每次迭代极小化目标泛函时,需要沿搜索方向pl计算搜索步长al,搜索方向的迭代格式与线性共轭梯度近似:
(7)
为了简化计算,我们选取Polak-Ribiere共轭梯度法[19]来极小化目标函数,则(7)式中有
(8)
其中,Cl为预调节因子。
在线性搜索过程中,如果搜索收敛,则新的搜索方向pl由(7)式计算;如果搜索失败,则pl取为最速下降方向(pl=-Clgl),打破和前面搜索方向的共轭性。
2.2 NLCG算法简化
在二维算法中,Rodi等[12]和Newman等[20]分别给出了预调节因子的构造方案,其中Rodi等用如下方法构造预调节因子:
(9)
式中:γl是特定的标量。应用线性共轭梯度法,通过对方程组(10)中h的求解将预调节因子作用于梯度向量:
(10)
在具体实现时,这需要增加很大的计算量,考虑到一维反演的复杂程度远低于二维,为了使反演算法更加快速,尝试在一维反演中将Cl取为单位矩阵,即不再进行预调节。
最优步长是反演中最重要的变量。二维反演中使用单变量高斯-牛顿线性搜索方法,在每一次共轭梯度循环中进行多次高斯-牛顿迭代,通过与模型进行实时对比确定最优步长。这种方法虽然能够得到较好的步长,但是需要重复调用正演函数及其它反演参数,对一维反演而言增加了太多的计算量,得不偿失。因此我们尝试用单步线性搜索法求步长,即
(11)
这样求得的步长虽然不是最优结果,但经验证其反演效果能够达到预期,最主要的是减少了很多的计算量,相对于高斯-牛顿迭代节省了至少1/3的时间。就一维反演而言这样的简化是合适的,但对于二维以上大数据量的反演,这样的简化会减缓目标函数的收敛速度,增加迭代次数,影响反演效率,甚至导致反演失败。
简化后的NLCG算法在每次迭代过程中采用Polak-Ribiere共轭梯度法计算线性搜索方向,在每一搜索方向上用单步线性搜索法求取最优步长,得到新的模型,在规定拟合差或迭代次数范围内结束循环,详细流程如图1所示。

图1 非线性共轭梯度反演流程
2.3 理论模型算例分析
设计了多个理论模型来验证NLCG反演算法的有效性。以7层水平层状介质模型为例,将正演视电阻率计算值加5%的随机噪声作为观测值,初始模型层厚按一定比例递增,每层电阻率取视电阻率平均值,根据反演结果不断调整正则化因子,以使反演效果达到最佳。同时,为避免模型出现较大的跳跃,尝试对增量进行压制(增量乘以限制系数),这样得到的反演曲线比较光滑。
图2a为7层模型反演结果,可以看出,NLCG算法的适应性和稳定性比较好,在有一定噪声干扰的情况下,电性层的划分以及每层的电阻率值均能较为准确地与设计模型对应,尤其是浅层很薄的电性层依旧能被准确识别,且不会出现冗余构造,说明NLCG算法反演精度和分辨率较高,在小构造的识别中具有一定的优势。图2b中拟合曲线能够较好反映观测数据中微小的变化,说明正则化因子的存在很好地兼顾了模型粗糙度和拟合度。
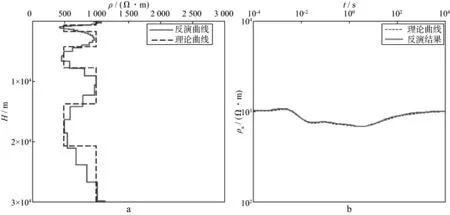
图2 7层水平层状介质模型反演结果a 反演结果; b 拟合曲线
图3为3层和4层层状介质模型的目标函数收敛曲线,可以看出,对于不同的模型,大约迭代10次以后目标函数就能够趋于收敛且稳定,说明NLCG算法的收敛速度较快,所需的迭代次数较少,在计算方面具有一定的优势。
NLCG算法能够节省运算时间、提高反演效率,同时又能保证反演的分辨率,因此适用于大规模的非线性一维反演计算。
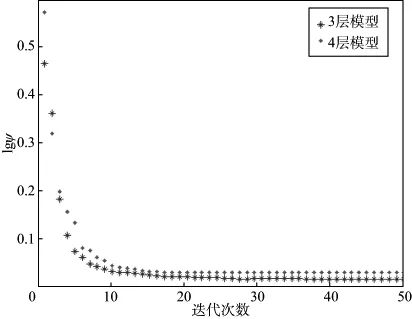
图3 目标函数收敛曲线
3 NLCG一维反演算法改进
通过模型算例分析可以看出,NLCG算法反演效果很好,具有较高的分辨率。但是该算法需要满足一些前提条件,即最优的初始模型和最合适的正则化因子,尤其是简化后的算法对初始模型的依赖度很高。为了达到最好的反演效果,在每次试验中都需要不断调整初始模型和正则化因子,这在一定程度上降低了反演的效率,增加了工作量。因此,以最小的计算量和最短的时间来选择最优的初始模型和正则化因子成为提高NLCG算法反演效率的关键。
3.1 基于Bostick的NLCG反演
由于NLCG算法对初始模型的依赖度很高,因此需要找到一种简便的反演算法为其提供初始模型。Bostick反演法无疑是最好的选择。
Bostick反演作为一种近似的反演方法,使用相位进行反演,基本公式为

(12)
式中:H为地层深度,φ为相位。根据测得的视电阻率和相位,用(12)式可以计算出深度-电阻率模型。该方法计算速度快,不需要初始模型,也不需要反复迭代[21],虽然反演精度很低[22],却是一种为其它反演方法提供初始模型的快捷方法。
3.2 正则化因子的自适应迭代调整
正则化因子作为权重因子起到了平衡目标函数和模型约束的作用。当它比较大时,模型比较光滑,但数据拟合度较差,较小时主要拟合实测数据,模型比较粗糙。因此选择合适的正则化因子成为提高反演效果的关键。
在上述算法中,正则化因子是在程序中给定的,按照反演效果不断进行修改,这样需要大量的运算,降低了算法的效率。因此,我们尝试自动调整正则化因子,以加快算法的运行效率。
考虑到正则化因子在极小化数据拟合差范数和模型范数之间起到折中的作用,参考陈小斌等[23]提出的自适应正则化因子调整方法,结合算法实际,提出了如下调整方案。
令公式(3)中Ψ1=eTV-1e;Ψ2=mTLTLm,则Ψ=Ψ1+λΨ2。其中Ψ1为观测数据目标函数;Ψ2为先验约束条件的目标函数,即模型粗糙度函数;λ为正则化因子。以迭代的方式调整正则化因子:
(13)
从公式(13)可以看出,虽然在每次共轭梯度循环时重新计算了正则化因子,但是不会增加新的计算量,因为计算所需的Ψ1和Ψ2在共轭循环中已经计算过。
设计多个理论模型验证了改进算法的有效性,同时验证了需要给定的正则化因子初始值λ0。以4层KH模型为例,经过不断试验,发现大多数的模型只需将初始值给定1~5中的一个数即可。
图4为4层KH模型改进后NLCG算法反演结果。可以看出,改进后的NLCG算法具有较好的分辨率,反演结果能够与模型基本对应,分层效果较好,尤其是低阻层精度比较高。
改进后的NLCG算法不再需要人为地对初始模型和正则化因子进行调整,加快了反演的速度,但是该算法对于高阻层反演精度相对较低,而且由于Bostick反演模型对于深层介质厚度变化反应较快,导致深层电性层划分具有一定的偏差。
3.3 反演优化
NLCG反演对于高阻层的分辨率较差的情况具体表现为浅层高阻出现震荡,深层高阻拟合精度差(图2,图4)。增加迭代次数可以使深层高阻反演精度有所提高,但是浅层高阻震荡加剧。迭代次数过少则深层高阻反演精度较差,二者不可兼顾,且随着模型复杂度增加,高阻层的分辨率会进一步降低。所以,我们对反演结果做一次优化,对优化后的结果再做一次反演(图5)。
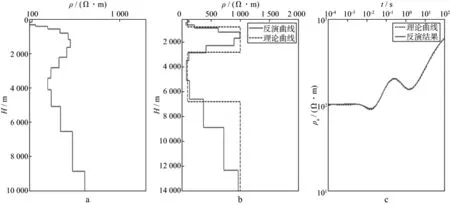
图4 4层KH模型改进后NLCG算法反演a Bostick反演的初始模型; b 改进后的NLCG反演结果; c 拟合曲线

图5 NLCG反演优化效果a NLCG反演结果; b 二阶微分曲线; c 优化NLCG反演结果
先做5~10次的NLCG反演,得到较为粗糙的反演模型,对反演曲线做拟合后求微分(二次微分),利用微分曲线极值点(零点)对应反演曲线拐点划分出地下介质的电性层,确定电性分界面;然后将每一电性层继续分成若干薄层,低阻层的划分可以较厚,高阻层的划分相对较薄,薄的高阻层划分有利于快速收敛,高、低阻层差异性划分也能保证电性分界面的清晰,由于电性层的划分不完全准确,相邻电性层的厚度二次划分不宜差距过大,每一层的电阻率可以取该层反演电阻率平均值,也可统一取视电阻率平均值。将优化后的结果作为初始模型再进行一次反演,只需较少的迭代次数就可以达到很高的反演精度,使反演结果的分辨率进一步提高(图5)。
4 实际资料处理效果分析
为了验证NLCG算法对于实测资料反演的有效性,我们对A地区井旁测点的大地电磁数据进行了反演,并与钻井资料和电测井资料进行了对比。以Bostick反演结果为初始模型,未进行二次反演优化,结果如图6所示。
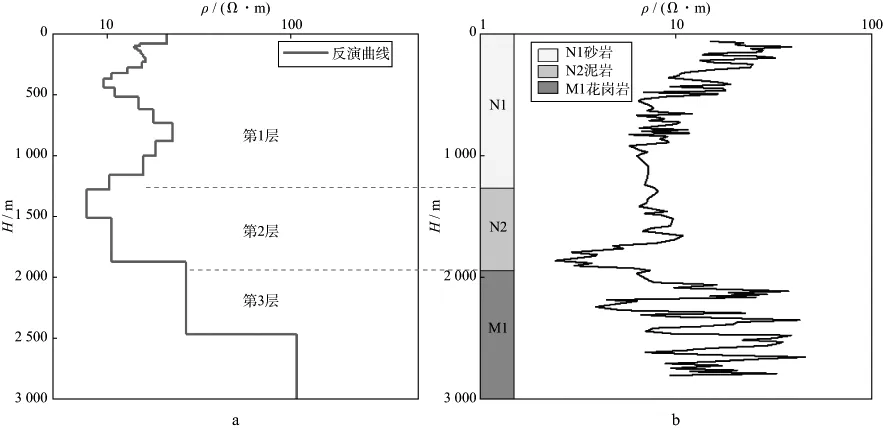
图6 A地区实际MT资料反演效果分析a 实际资料反演结果; b 钻井岩性及电测井曲线
从反演结果与钻井数据对比可以看出,反演结果与地下地层结构基本对应:第1层为高阻层,对应于砂岩;第2层为低阻层,反映的是泥岩;第3层对应高阻花岗岩,电阻率比较高。实际资料反演结果表明,改进的NLCG反演算法是有效且比较精确的,反演速度较快,与理论模型反演得出的结论一致。将改进后的NLCG算法用于实际资料电性结构的划分以及拟二维反演解释,结果是可靠的。
5 与其它算法的比较
传统的反演方法中,梯度法(最速下降法)只用到模型的梯度,即一阶导数,算法过于简单,在极小点附近收敛不好;高斯-牛顿算法虽然在极小点收敛比较快,但是其计算量与模型参数量和观测数据量成正比,在大数据量反演中需要的内存比较大。传统方法最大的不足是只考虑了拟合优度而没有考虑模型的粗糙度。NLCG算法既保证了在极小点附近收敛比较快,又引入了模型粗糙度,反演的稳定性较好,分辨率较高。
以5层层状介质模型为例,将改进的NLCG算法与马夸特法[5]进行了对比(图7)。采用相同的初始模型:层厚按比例递增,每层电阻率取为视电阻率平均值。由图7可见,马夸特法对于深部地层的分辨率较低,NLCG法优于马夸特法,尤其是低阻层精度较高,而且随着模型复杂度增加,NLCG算法的优势越来越明显。
采用改进的NLCG法和Occam反演法对A地区井旁测点的大地电磁数据进行了反演对比,两种方法都是以Bostick反演结果为初始模型,迭代35次,结果如图8所示。对比NLCG和Occam反演结果可以看出,二者与观测数据的拟合都比较好,NLCG反演的结果分层更加清晰,且不会出现Occam反演结果所显示出的异常高阻层,反演结果更接近实际,在地下电性结构的划分中可靠度和可信度更高。

图7 5层水平层状模型的马夸特法(a)和NLCG法(b)反演结果对比

图8 A地区实际MT资料反演结果对比a Occam与NLCG反演结果; b 拟合曲线
6 结束语
理论研究和实际资料处理结果表明,经过优化的NLCG算法能够节省运算时间、提高反演效率,同时又能保证反演的分辨率,适合大规模的非线性一维反演计算。
1) 根据目标函数自动调整正则化因子,避免了对正则化因子的不断尝试反演,提高了运行效率。
2) 简化了预处理因子和最优步长的计算,用单步线性搜索法代替迭代法求最优步长,使NLCG算法更加高效快捷。
3) 对一次反演结果优化后进行二次反演,进一步提高了反演结果的分辨率。
致谢:在与中国海洋大学罗鸣探讨算法的过程中,笔者受益匪浅,在此向他表示感谢。
参 考 文 献
[1] 石英俊,刘国栋,吴广耀,等.大地电磁测深法教程[M].第1版.北京:地质出版社,1985:1-110
Shi Y J,Liu G D,Wu G Y,et al.The magnetotelluric sounding tutorial[M].1st ed.Beijing:Geological Publishing House,1985:1-110
[2] Tikhonov A N.On determining electrical characteristics of the deep layers of the earth’s crust[J].Dokl Akad Nauk,1950,73(2):95-297
[3] Cagniard L.Basic theory of the magnetotelluric method of geophysics prospecting[J].Geophysics,1953,18(3):605-635
[4] 陈乐寿,王光锷.大地电磁测深法[M].第1版.北京:地质出版社,1990:1-56
Chen L S,Wang G E.The magnetotelluric sounding method[M].1st ed.Beijing:Geological Publishing House,1990:1-56
[5] Marquardt D W.An algorithm for least-squares estimation of nonlinear parameters[J].Journal of the Society of Industrial and Applied Mathematics,1963,11(2):431-441
[6] 师学明,王家映.一维层状介质大地电磁模拟退火反演法[J].地球科学,1998,23(5):542-545
Shi X M,Wang J Y.One dimensional magnetotelluric sounding inversion using simulated annealing[J].Earth Science,1998,23(5):542-545
[7] Constable S C,Parker R L,Constable G C.Occam’s inversion:a practical algorithm for generating smooth models from electromagnetic sounding data[J].Geophysics,1987,52(3):289-300
[8] 韩波,胡祥云,何展翔.大地电磁反演方法的数学分类[J].石油地球物理勘探,2012,47(1):177-187
Han B,Hu X Y,He Z X.Mathematical classification of magnetotelluric inversion method[J].Oil Geophysical Prospecting,2012,47(1):177-1877
[9] 陈向斌,吕庆田,张昆.大地电磁测深反演方法现状与评述[J].地球物理学进展,2011,26(5):1607-1619
Chen X B,Lv Q T,Zhang K.Review of magnetotelluric data inversion methods[J].Progress in Geophysics,2011,26(5):1607-1619
[10] Madden T M,Mackie R L.Three-dimensional magnetotelluric modeling and inversion[J].Proceedings of the IEEE,1989,77(2):318-333
[11] Mackie R L,Madden T R.Three-dimensional magnetotelluric inversion using conjugate gradients[J].Geophysical Journal International,1993,115(1):215-229
[12] Rodi W,Mackie R L.Nonlinear conjugate gradients algorithm for 2-D magnetotelluric inversion[J].Geophysics,2001,66(1):174-187
[13] Newman G A,Alumbaugh D L.Three-dimensional magnetotelluric inversion using non-linear conjugate gradients[J].Geophysical Journal International,2000,140(2):410-424
[14] 李卫东.大地电磁反演方法评析及其在地热勘探中的应用研究[D].北京:中国地质大学,2006
Li W D.Assessment of magnetotelluric sounding inversion method and research for geothermal exploration[D].Beijing:China University of Geosciences,2006
[15] 柳建新,童孝忠,郭荣文,等.大地电磁测深法勘探—资料处理、反演与解释[M].第1版.北京:科学出版社,2012:1-111
Liu J X,Tong X Z,Guo R W,et al.The magnetotelluric sounding exploration—data processing,inversion and interpretation[M].1st ed.Beijing:Science Press,2012:1-111
[16] 吉洪诺夫.不适定问题的解法[M].王秉忱译.第1版.北京:地质出版社,1979:1-160
Tikhonov A N.Solution methods for the ill-posed problems[M].Wang B C translator.1st ed.Beijing:Geological Publishing House,1979:1-160
[17] 胡祖志,胡祥云,何展翔.大地电磁非线性共轭梯度拟三维反演[J].地球物理学报,2006,49(4):1226-1234
Hu Z Z,Hu X Y,He Z X.Pseudo-three-dimensional magnetotelluric inversion using nonlinear conjugate gradients[J].Chinese Journal of Geophysics,2006,49(4):1226-1234
[18] 万汉平.大地电磁测深TE和TM极化模式对比研究[D].四川:成都理工大学,2010
Wan H P.Comparison of magnetotelluric TE and TM polarization modes[D].Sichuan:Chengdu University of Technology,2010
[19] 王家映.地球物理反演理论[M].第2版.北京:高等教育出版社,2002:1-182
Wang J Y.Inverse theory in geophysics[M].2nd ed.Beijing:Higher Education Press,2002:1-182
[20] Newman G A,Boggs P T.Solution accelerators for large-scale three-dimensional electromagnetic inverse problems[J].Inverse Problems,2004,20(6):151-170
[21] 周虬.一种简易的一维大地电磁测深反演方法—博斯蒂克法反演及其应用[J].石油地球物理勘探,1985,20(1):80-88
Zhou Q.A simple one-dimensional magnetotelluric inversion methods—Bostick inversion and its application[J].Oil Geophysical Prospecting,1985,20(1):80-88
[22] 徐新学,赵宪堂,王宝勋,等.大地电磁测深资料常规反演方法的应用现状及进展[J].地质调查与研究,2004,27(增刊):71-74
Xu X X.Zhao X T,Wang B X,et al.The application status and progress of magnetotelluric sounding data regular inversion[J].Geological Survey and Research,2004,27(S):71-74
[23] 陈小斌,赵国泽,汤吉,等.大地电磁自适应正则化反演算法[J].地球物理学报,2005,48(4):937-945
Chen X B,Zhao G Z,Tang J,et al.An adaptive regularized inversion algorithm for magnetotelluric data[J].Chinese Journal of Geophysics,2005,48(4):937-945

