Toeplitz-Hausdorff定理的新证明

张 云, 陈冬君, 叶永升

(淮北师范大学 数学科学学院, 安徽 淮北 235000)

数值域是矩阵理论和算子理论中一个基本的研究对象.它在量子信息论、模式识别等许多领域都有着广泛的应用[1-5].目前,关于数值域方面的文献非常丰富,同时也有一些关于数值域方面的专著,见文献[6].下面首先给出数值域的定义.

设A是n阶复方阵,矩阵A的数值域定义为集合

W(A)={x*Ax|‖x‖=1,x∈Cn}.

式中,Cn为n维欧氏空间,‖x‖表示x的欧氏范数.

不难看出,任何方阵的数值域都是复数集的一个有界子集.同时,矩阵的谱都含在其数值域之中.数值域最基本的性质是它是凸集,即著名的Toeplitz-Hausdorff定理.关于这条性质的证明,已引起很多数学家的兴趣,比如,Halmos就给出了漂亮的证明.绝大多数的证明方法是通过转化为2×2阶的复矩阵来考虑.在这种特殊情形下,证明二阶方阵的数值域是一个椭圆盘,即如下著名的椭圆定理.

C.K.Li给出了椭圆定理漂亮的新证明,参见文献[7].

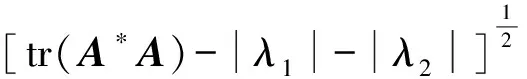
本文利用类似于Moyls和Marcus在文献[8]中的想法,给出了Toeplitz-Hausdorff定理一种直接且简单的证明.

首先列举数值域的一些基本且有用的性质.

设A是n阶复方阵,则

(1)W(αI+βA)=α+βW(A) (α,β∈C);

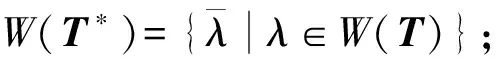
(3)W(U*AU)=W(A),其中,U为任意的酉矩阵.

Toeplitz-Hausdorff定理设A是n阶复方阵,则它的数值域W(A)是凸集.

证明 考虑A的笛卡儿分解:

A=G+iH,

记单位球

S={x∈Cn|‖x‖=1},

令φ(z)=z*Gz,ψ(z)=z*Hz,z∈S,将C等同于R2,于是

W(A)={(φ(z),ψ(z))|z∈S}.

由于G是Hermite矩阵,则由谱分解定理知,存在一个酉矩阵U,使得

U*GU=diag(μ1,…,μn).

式中,μ1,…,μn是G的特征值.因此,对于给定的z0=(z1,…,zn)T∈S,有

从而,只需证明对于给定的z0∈S,ψ(φ-1(φ(z0)))在平面R2上连通即可.

由于ψ(z)是实值连续函数,因此,只需证φ-1(φ(z0))在单位球S上连通即可.事实上

对于任意给定的x,y∈φ-1(φ(z0)),下面证明在集合φ-1(φ(z0))中存在一条从x到y的路.将证明分为三步:在集合φ-1(φ(z0))中存在一条从x到|x|的路;在集合φ-1(φ(z0))中也存在一条从y到|y|的路;在集合φ-1(φ(z0))中也存在一条从|x|到|y|的路.

设x=(x1,…,xn)T=(|x1|eiθ1,…,|xn|×eiθn)T,定义|x|=(|x1|,…,|xn|),则

|x|∈φ-1(φ(z0)).

令

α(t)=(|x1|ei(1-t)θ1,…,|xn|ei(1-t)θn)T,

式中,0≤t≤1.容易验证

α(0)=x,α(1)=|x|,

且α(t)∈φ-1(φ(z0)),∀t∈[0,1],

从而,α(t)在集合φ-1(φ(z0))中存在一条从x到|x|的路.

同理可证,在集合φ-1(φ(z0))中也存在一条从y到|y|的路.

下证在集合φ-1(φ(z0))中也存在一条从|x|到|y|的路.假设|x|=(|x1|,…,|xn|),|y|=(|y1|,…,|yn|),令

式中,0≤t≤1.容易验证

β(0)=|x|,β(1)=|y|,

因此,β(t)在集合φ-1(φ(z0))中存在一条从|x|到|y|的路.

综上所述,φ-1(φ(z0))是道路连通的.由于H是Hermite矩阵,从而ψ(z)是实值连续函数.根据连续函数的性质知,连续函数把连通集映成连通集,从而ψ(φ-1(φ(z0)))是R上的区间.注意到在R2中集合的旋转和平移不改变自身的凸性,因此,每一条与W(A)相交的直线,它们的交集都是区间.故W(A)是凸集.

参考文献:

[1]Ando T, Li C K. The Numerical Range and Numerical Radius[J]. Linear and Multilinear Algebra, 1994,37(1/2/3):221-223.

[2]Donoghue W F. On the Numerical Range of a Bounded Operator[J]. The Michigan Mathematical Journal, 1957,4(3):261-263.

[3]Halmos P R. A Hilbert Space Problem Book[M]. Princeton: van Nostrand, 1967.

[4]Horn R A, Johnson C R. Matrix Analysis[M]. Cambridge: Cambridge University Press, 1991.

[5]王跃华,王洁英. 关于不等式几种常见证明方法的探究[J]. 沈阳大学学报:自然科学版, 2013,25(5):428-430.

(Wang Yuehua, Wang Jieying. Several Common Methods of Proof of Inequality[J]. Journal of Shenyang University:Natural Science, 2013,25(5):428-430.)

[6]Gustafson K E, Rao D K M. Numerical Range: The Field of Values of Linear Operators and Matrices[M]. New York: Springer, 1997.

[7]Li C K. A Simple Proof of the Elliptical Range Theorem[J]. Proceedings of the American Mathematical Society, 1996,124(7):1985-1986.

[8]Moyls B N, Marcus M D. Field Convexity of a Square Matrix[J]. Proceedings of the American Mathematical Society, 1955,6(6):981-983.