具有广义FGM Copula的复合泊松过程的净保费研究

方 颢，王传玉，戴泽兴

(安徽工程大学 数理学院，安徽 芜湖 241000)

近年来，用Copula方法刻画随机变量之间的相依关系在保险精算和风险理论等领域越来越普遍(例如Cossette[1]、Albreeher等[2-3])。Copula函数是一种连接函数，它将一个联合分布与该联合分布的各个边缘分布连接在一起。Nelsen[4]对Copula函数作了详细的介绍并举例Copula函数在保费定价中的广泛应用。徐付霞和董永权[5]以FGM Copula及其联合生存函数为基础，拓展出了一系列二参数三次幂的广义FGM Copula，使FGM Copula的种类变得更加繁多，应用范围更为广泛。

2012年，Marri和Furman[6]考虑了索赔额{Yn}n≥1和等待时间{Wn}n≥1之间为FGM Copula相依的情形，对相应的总索赔额，记为Xt,θ，进行了研究。文献[7]将其中的FGM Copula推广为广义FGM Copula，建立了Esscher定价公式。本文在广义FGM Copula条件下，利用Laplace变换、Laplace逆变换等方法求出了零利息和非零利息力下总索赔额Xt,θ的净保费表达式，最终得到Esscher定价泛函的表达式，推广了文献[6]的结论。

1 相依复合泊松过程及其矩母函数

在研究Esscher保费定价时，首先需要计算索赔额Xt的矩母函数。下文中我们假定：

A.等待时间Wn，n≥1独立同分布；

B.等待时间的随机变量W服从指数分布，期望E[W]=1/λ；

C.索赔额Yn，n≥1独立同分布，其累计分布函数F和概率密度函数f的值为正实数。且对应矩母函数M(h)=E[ehY]<∞,h∈R；

D.Wn、Yn之间的相依性用二元五次广义Farlie-Gumbel-Morgenstern (FGM) Copula来刻画：

Cθ(u,v)=uv+θuv2(1-u)(1-v),

-1≤θ≤1

其中(u,v)∈[0,1]×[0,1]。图1为θ分别取-1、0、1的图像。

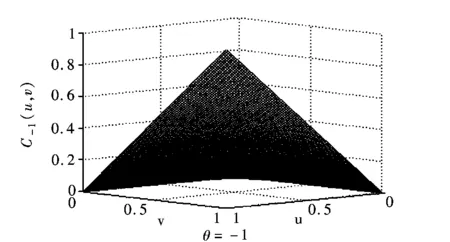
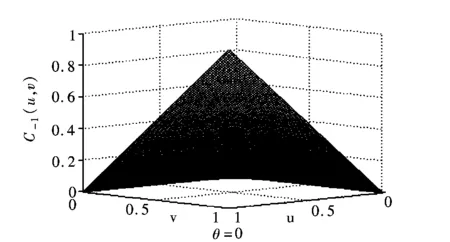
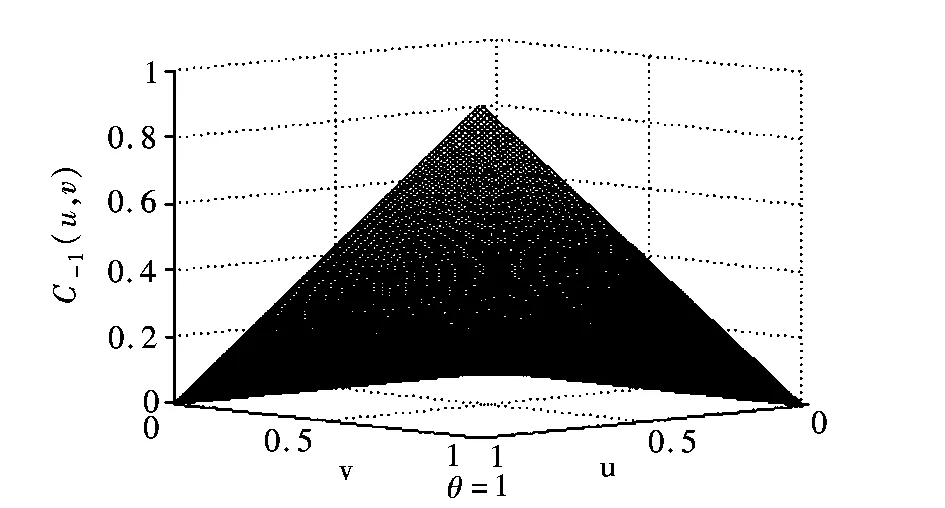
图1 不同θ下的FGM CopulaFig.1 FGM Copula with different θ

为了区别相依和独立的复合泊松过程，本文用Xt,θ来表示前者，用Xt表示后者。

定义1[8]以Y表示单次索赔额的随机变量，其累积分布函数为F，w:[0,+∞)→[0,+∞)是一个加权函数，使E[w(Y)]有限且严格为正。定义加权分布函数为：

由文献[7]可知(W,Y)概率密度函数为

fW,Y(w,y)=λe-λwf(y)+θ[f(y)-

fw(y)](4λe-2λw-3λe-3λw-λe-λw)

其中fw(y)是Y对应的加权概率密度函数，从上式可以看出fw(y)和f(y)有很大差别，我们有以下命题：

命题1[6]设Y～F,Yw～Fw,w(y)=2F(y),则Mw(h)=E[ehYw]≥M(h),h∈R。

基于假设A-D，我们得到以下定理：

定理1[7]假设A-D成立，则相依复合泊松过程Xt,θ的矩母函数为

MXt,θ(h)=

h∈R

(1)

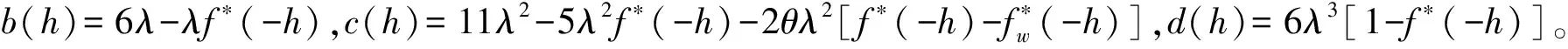
2 零利息力和非零利息力下的净保费

定理2 通货膨胀和利率相等的零利息力下，净保费可以表示为

(2)

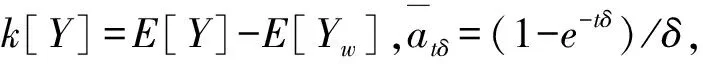
t>0,δ>0。

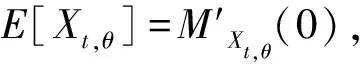
b(h)=5λ,c(h)=6λ2,d(h)=0。由根与系数关系得

(3)

解得p1,λ,θ(0)=-2λ,p2,λ,θ(0)=-3λ,

p3,λ,θ(0)=0。对(3)式求导可得

代入(1)式中求导得

然而在很多现实情形中，我们需要考虑通货膨胀和利率组成的非零利息力。很多学者对非零利息力下的保费索赔进行了研究(例如，Léveillé等[9-10])。对正利息力δ，总索赔可记为

定理3 设非零利息力为δ，净保费可以表示为

(4)

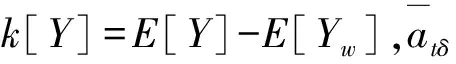
证明：由Bargés[11]的3.1节，得到Xt,θ,δ的更新方程如下

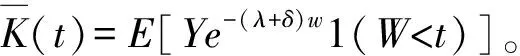
类似Marri[6]定理2.1的证明，运用Volterra积分方程的卷积形式，令G(t)=E[Xt,θ,δ]可得

g(w)=λe-(λ+δ)w

g*(p)≠1

由假设B可知

结合假设D得

E[Xt,θ,δ]=

即为(2)式。

3 Esscher定价泛函

对索赔额和等待时间相依的复合泊松过程Xt,θ,δ，非零利息力下Esscher定价泛函定义为

(5)

易知，lim∏h[Xt,θ,δ]=E[Xt,θ,δ]；且当h≥0，Esscher定价泛函值是非负的。事实上，由Xt,θ,δ和ehXt,θ,δ正象限相关，有

定理4 设Xt,θ,δ满足假设A-D，记

(6)

j=1,2,3

则Xt,θ,δ的Esscher定价泛函可以表示为

(7)

证明：对Xt,θ,δ关于h求导得

4 结论

本文考虑索赔额和等待时间是相依复合泊松过程的情形，两者之间相依性由广义FGM Copula来刻画。仿造文献[6]的方法，利用Laplace变换，Volterra积分方程的卷积形式，Laplace逆变换等方法求解出零利息力和非零利息力下净保费的表达式，最后给出了其Esscher定价泛函的表达式。

参考文献：

[1] Cossette H, Marceau E, Marri F. On the Compound Poisson Risk Model with Dependence Based on a Generalized Farlie-Gumbel-Morgenstern Copula[J].Insurance:Mathematics and Economics, 2008,43(3):444-455.

[2] Albreeher H, Boxma O. J.A Ruin Model with Dependence Between Claim Sizes and Claim Intervals[J].Insurance:Mathematics and Economics 2004,35(2):245-254.

[3] Albreeher H, Teugels J. Exponential Behavior in the Presence of Dependence in Risk Theory[J].J.Appl.Prob,2006,43(1):265-285.

[4] Nelson R B. An introduction to Copulas[M].New York:Springer, 1999.

[5] 徐付霞,董永权.FGM Copula的另一种拓展[J].应用数学,2011,24(1):84-90.

[6] Marri F, Furman E. Pricing compound Poisson processes with the Farlie-Gambel- Morgenstern dependence structure[J].Insurance:Mathematics and Economics, 2012, 51(1): 151-157.

[7] 方颢,王传玉,张大伟.具有广义FGM相依结构的复合泊松过程的Esscher定价泛函[J].数学理论与应用，2013,33(3):76-81.

[8] Furman E, Zitikis R. Weighted premium calculation principlesp[J].Insurance: Mathematics and Economics, 2008,42(3):459-465.

[9] Léveillé G, Garrido J. Moments of compound renewal sums with discounted claims[J].Insurance: Mathematics and Economics, 2001,28(2):217-231.

[10] Léveillé G, Garrido J, Wang Y F. Moment generating functions of compound renewal sums with discounted claims[J].Scandinavian Actuarial Journal,2009,2(1):98-110.

[11] Bargés M, Cossette H, Loisel S, et al. On the moments of the aggregate discounted claims with dependence introduced by an FGM copula[J].ASTIN Bulletin,2011,41(1):215-238.