基于边缘信息与偏移场矫正的多相Chan-Vese图像分割模型

周三平, 滕炯华, 黄保山, 徐婧林

(西北工业大学 自动化学院, 陕西 西安 710172)

传统的基于几何活动轮廓的水平集方法仅利用了图像的局部信息,在分割边缘模糊或者含有噪声的图像时,通常不能得到令人满意的结果。而基于Chan-Vese模型的水平集分割方法[1],依赖的是同质区域的全局信息,能够有效分割边缘模糊的图像。Chan-Vese模型属于单项水平集二相图像分割模型,不能将1幅图像中的多个目标同时分割开来,为了弥补这个不足,2002年Chan和Vese提出了多相Chan-Vese模型[2]。多相Chan-Vese模型在分割1幅图像的多个目标时得了极大成功,并且对噪声不敏感。但是,该模型存在如下缺点:1)不能分割灰度不均匀的图像[3],因为模型假设图像灰度在各个区域上是分段常值的,所以在分割灰度不均匀的图像时,演化曲线通常不能逼近目标的真实边缘;2)对初始轮廓线的位置比较敏感,在分割稍微复杂的图像时,曲线的演化结果严重依赖初始轮廓曲线的位置,不同的初始轮廓线可能会得到不同的分割结果,甚至会导致分割失败;3)重新初始化问题[4],为了保证水平集函数在演化的过程中保持光滑性和符号距离函数的特性,需要定期地将水平集函数重新初始化为符号距离函数,消耗了大量的时间。

为了解决这些问题,很多改进的模型不断地被提出。Li Chunming等[5]提出利用核函数将图像的局部信息加入到图像分割模型中,提出了LBF模型,增强了模型分割灰度不均匀图像的能力。Wang Li等[6]综合运用了Chan-Vese模型中的全局信息和LBF模型中的局部信息,提出了LGIF模型,提高了模型对初始轮廓的适应的能力。无论是LBF模型,还是LGIF模型,都是Chan-Vese模型在图像二相分割方面的改进,不能够同时将图像中的多个目标分割开来。

本文提出了一种基于边缘信息与偏移场矫正的图像多相分割模型。首先,利用对数变换将乘性偏移场转化成线性偏移场,然后通过核函数引入局部灰度信息,最后利用变分法建立了基于区域信息的偏移场矫正模型。此外,利用水平集函数与图像梯度的方向信息对传统的边缘指示函数[7]进行了改进,综合利用了图像的梯度信息,重建了边缘指示函数。对比实验表明我们提出的模型能够取得令人满意的分割结果。

1 多相Chan-Vese模型

1.1 区域特征函数

Chan-Vese模型是属于单项水平集的二相图像分割模型,该模型用一个水平集函数,能够描述图像的二相分割,如图1a)所示。当图像具有较复杂的几何特征,例如有多个目标、多相边界、复杂的拓扑结构时,利用单项水平集模型通常不能够取得令人满意的分割结果。2002年Chan和Vese对他们先前提出的无边缘活动轮廓模型进行了推广,提出了Chan-Vese多相水平集图像分割模型。该模型采用n个水平集函数将图像划分为2n个区域,可以很自然地避免多个水平集之间的重叠与漏分,并且得到的能量函数具有对称的形式。图1b)给出了用2个水平集函数实现四相分割时,区域的划分情况。

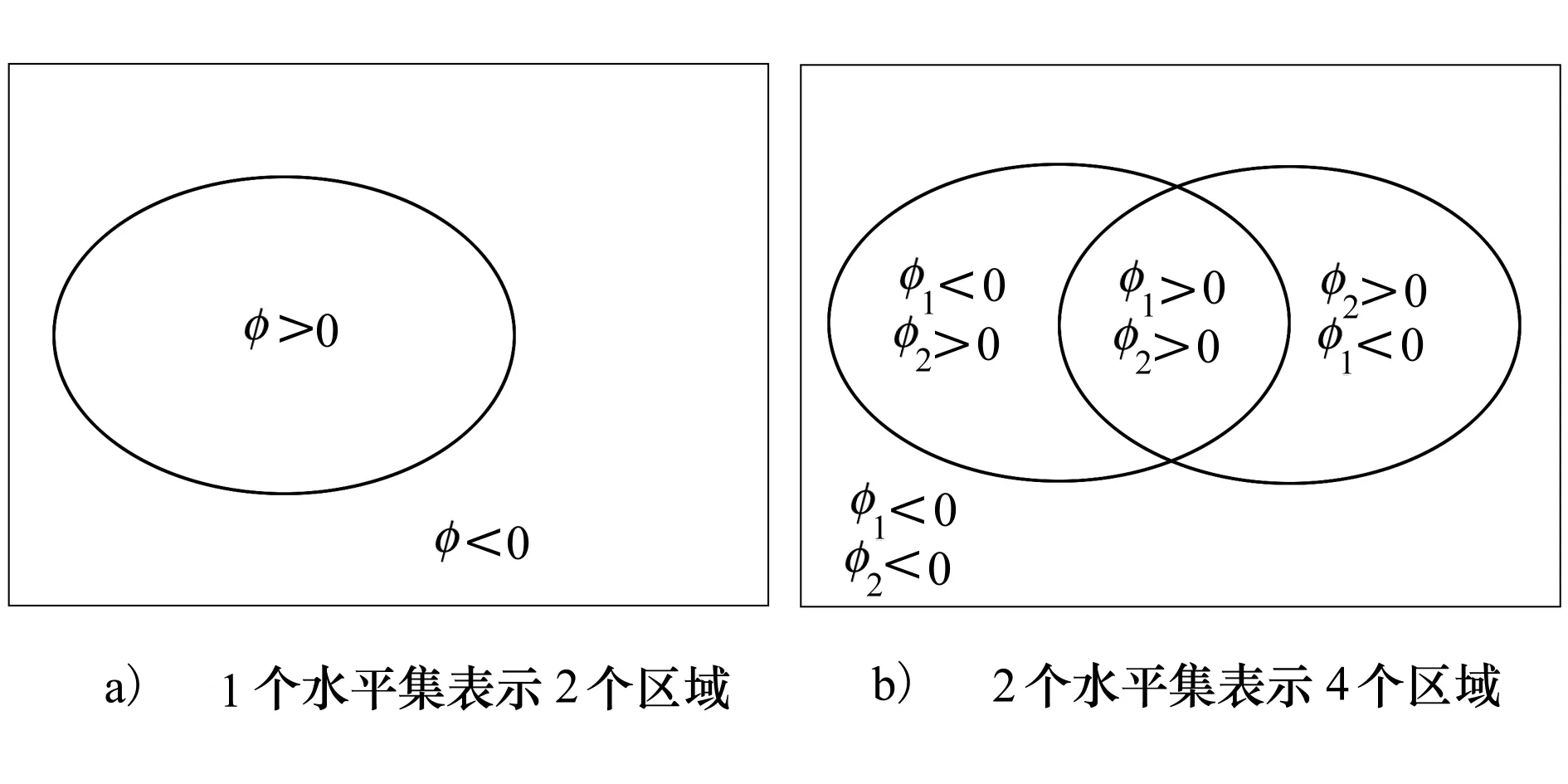
图1 区域划分的水平集表示

为了更加清楚、简洁地描述区域的划分情况,我们定义如下的区域特征函数:

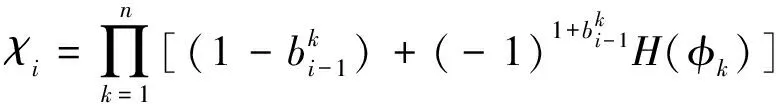
(1)

1.2 多相Chan-Vese模型

多相Chan-Vese模型采用1.1节中的分割策略,即利用n个水平集函数将1幅图像划分成2n个区域。当利用2个水平集函数实现图像的四相分割时,相应的能量泛函为:

(2)

式中：u为长度项系数,c1、c2、c3、c4分别代表图像在4个区域中的灰度均值,χ1、χ2、χ3、χ4分别表示4个区域的特征函数,φ1、φ2为水平集函数,δ(φ)为Dirac函数,为梯度算子。

多相Chan-Vese模型利用了图像的全局信息,能够自然地处理图形拓扑的变化,且能够在较大范围内收敛。但是,当区域χ1、χ2、χ3、χ4中图像的灰度不均匀时,那么灰度均值c1、c2、c3、c4就可能会和图像的原始灰度值相差很大。如果没有引入图像的局部信息,多相Chan-Vese模型分割灰度不均匀的图像时很难取得较好的分割效果。

2 偏移场修正的多相模型

2.1 灰度不均匀性

由于成像设备的原因及外在条件的影响,我们获取的图像往往具有灰度不均匀性。虽然人眼无法察觉图像的灰度不均匀性,但是分割算法对这些虚假的变化却十分敏感。被广泛接受的灰度不均匀的假设是在图像域中加入一个随空间缓慢变化的光滑偏移场,可以用如下的数学模型来描述:

Y(k)=X(k)*G(k)+N

(3)

式中：Y(k)表示观测到的图像,X(k)表示真实的图像,G(k)表示光滑变化的偏移场,N表示噪声。为了简化计算,通常忽略噪声的影响,对模型做对数变换:

ln(Y(k))=ln(X(k))+ln(G(k))

(4)

令ln(Y(k))=y(k),ln(X(k))=x(k),ln(G(k))=β(k),则乘性偏移场模型可线性化为:

y(k)=x(k)+β(k)

(5)

2.2 核函数

在局部区域中灰度变化是可以分离的,但是在整个图像区域中灰度的变化却不易分离。因此在偏移场矫正的模型中需要利用核函数来描述局部区域。核函数通常满足如下特性:

1)K(u)=K(-u)

2)K(u)>K(v) if |u|<|v| and |u|→∞,K(u)→0

核函数K可以选择任何满足上述3个条件的函数。本文中,我们选择高斯核函数来描述图像的局部信息。高斯核函数定义如下:

(6)

式中：σ为高斯函数的标准差。假设ρ是以x为中心点的圆形邻域Oy的半径,即|x-y|2≤ρ2。当时ρ≥3σ时,高斯函数K(x-y)基本趋近于零。因此在实际计算时,我们约定:当ρ≥3σ时,K(x-y)=0。圆形邻域半径ρ应依据图像灰度不均匀的强度而定,当灰度不均匀效应比较明显的时,由于偏移场变化量比较大,所以应该选择较小的邻域半径ρ。

2.3 边缘指示函数

当演化曲线到达目标边缘时,边缘指示函数能够终止曲线的演化。在长度项中加入边缘指示函数能够有效地避免长度项陷入局部最小。传统的边缘指示函数仅利用了图像梯度的幅值信息,如(7)式所示。

(7)

在多相水平集图像分割模型中,当多个边缘出现在演化曲线附近时,演化曲线可能辨别不清哪一个边缘是对应的目标形成的,从而导致分割效果不理想。针对这个问题,本文利用水平集函数与图像梯度的方向信息对传统的边缘指示函数进行了改进,提出利用水平集函数φ的梯度方向表示演化曲线C的梯度方向,水平集函数与图像梯度之间的方向信息重建边缘指示函数:

S(I,φ)=H[(Gσ*I)·φ]

(8)

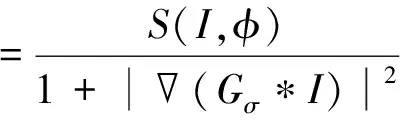
(9)

式中：H表示Heaviside函数,Gσ表示标准差为σ的二维Gaussian滤波算子,表示空间梯度算子。当演化曲线C到达目标附近时,水平集函数φ与图像边缘有相同的梯度,S(I,φ)=1,(Gσ*I)很大,g*≈0,曲线停止演化。当演化曲线C远离图像边缘时,(Gσ*I)≈0,如果水平集函数φ与图像边缘梯度方向相同,则S(I,φ)=1,g*≈1,曲线正常演化;如果水平集函数φ与图像边缘梯度方向不同,则S(I,φ)=0,g*≈0,曲线演化被抑制。所以,在图像边缘当1条演化曲线对应多个图像边缘时,边缘指示函数g*能够引导演化曲线选择正确的图像边缘。

2.4 正则项

水平集函数在演化一段时间后就会发生振荡,并且随着曲线的演化,误差会不断积累,最终造成演化曲线偏离目标的边缘。传统的解决方案是定期将水平集函数重新初始化为符号距离函数,该过程不但非常复杂,而且费时。本文在正则项中加入能量惩罚项来使得演化后的水平集函数自动趋近于符号距离函数,避免了重新初始化程序,如(10)式所示。

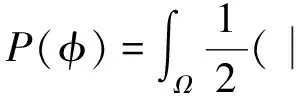
(10)

为了水平集函数在演化过程中保持光滑以及防止在最后分割结果中出现较小的孤立区域,需要在正则项中增加长度惩罚项:

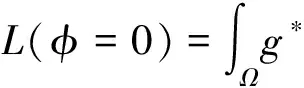
(11)

当演化曲线处于同质区域时,g*≈1演化曲线正常演化;当演化曲线处于目标边缘附近时,g*≈0演化进程被强制禁止,从而避免了长度项在目标附近取得局部极小值。

正则项通常由能量惩罚项与能量项组成,所以本文提出的正则项ER为:

(12)

2.5 水平集方法

将基于局部灰度信息的偏移场矫正模型及改进的正则项加入到多相Chan-Vese模型中,本文的提出的模型为:

(13)

式中：∂i为区域权重系数,νk为长度惩罚项系数,μk为能量惩罚项系数。Hε(z)为Heaviside函数H(z)非紧凑、光滑、严格单调的逼近,δε(z)为Dirac函数δ(z)正则逼近。

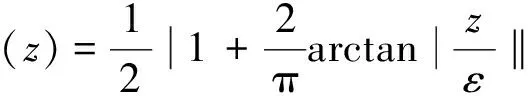
(14)

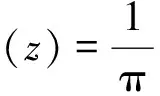
(15)

首先,利用变分法推导出偏移场β(y)及区域灰度均值ci的数学模型。能量泛函E(φ)可以看成是ci,β(y)以及水平集函数φ的函数,将ci,φ看作常量,求能量泛函E(φ)对β(y)的变分,即:

(16)

由(16)式可知,β(y)的一个特解为:

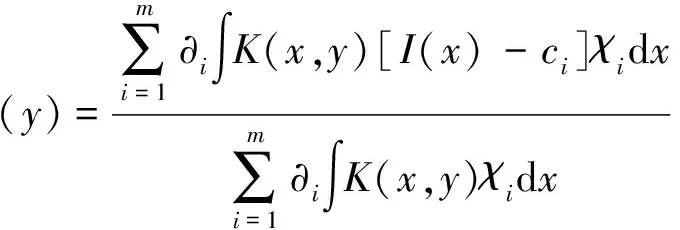
(17)

同理,将β(y),φ看作常量,求能量泛函E(φ)对ci的变分,可得ci为:

(18)

其次,利用梯度下降流最小化能量泛函E(φ),得到曲线的演化方程为:

(19)

(20)

3 实验结果与分析

本节通过自然图像与人工合成图像的分割实验,验证模型对初始轮廓位置的鲁棒性、噪声抑制能力及灰度不均匀图像的分割能力。本文实验环境为Matlab7.0,IBM PC,Pentium IV处理器,主频2.2GHz,RAM 2GB。本文所有的实验中,除了迭代次数和初始轮廓线的位置不同之外,其它参数规定如下:时间步长T=0.05,惩罚项权系数μ1=μ2=4,区域权重系数∂1=∂3=0.7,∂2=∂4=0.5,长度项权重系数ν1=ν2=6,网格间距h=1,ε=2(Hε(z),δε(z)参数),邻域算子函数K(x,y)的窗口大小为11×11。如无特别说明,实验中多相Chan-Vese模型与本文模型取相同的参数。

图2 灰度均匀图像分割

首先,分割灰度均匀图像来验证模型初始轮廓位置的鲁棒性。初始化时仅用初始轮廓曲线包围目标的一小部分,如图2a)、图2d)所示。经过40次的迭代,演化曲线成功的停止在了目标的真实边界上,如图2b)、图2e)所示。图2c)、图2f)为在相同的初始轮廓曲线条件下,多相Chan-Vese模型经过100次迭代的分割结果。可以看出,右上演化曲线误将其他2个目标的边缘当做是目标边缘,导致了越界分割。增加迭代次数至500次时,多相Chan-Vese模型分割结果仍如图2b)、图2e)所示,没有任何改善。

其次,对模型的噪声抑制能力进行验证。图3a)为零噪声的人工合成图像,图3b)在图3a)中加入方差为0.15的高斯噪声后初始化轮廓曲线位置,经过100次的迭代,目标成功地被从噪声图像中提取了出来,如图3c)所示。为了进一步凸显本文所提模型对噪声的抑制能力,在图3a)中分别加入方差为0.3、0.5的高斯噪声,经过200次的迭代,实验结果分别如图3d)与图3e)所示。可以看出,对于受强噪声污染的图像,本文算法仍能取得令人满意的分割效果。

最后,对模型分割灰度不均匀图像的能力进行验证。图4a)、图4d)为灰度不均匀的核磁共振图像初始化轮廓曲线,经过200次的迭代,图4b)、图4c)以及图4e)、图4f)分别给出了多相Chan-Vese模型和本文所提模型的分割结果。图4b)中,多相Chan-Vese模型外侧轮廓线发生了越界情况,并且图4e)的分割也不完全。2组实验,本文模型都能取得比较满意的分割效果。图5给出了偏移场修正前后图像的灰度直方图,可以看出修正后图像的灰度直方图呈多峰状分布,表明在同质区域内灰度值趋近于某一常值,符合Chan-Vese模型的基本假设。

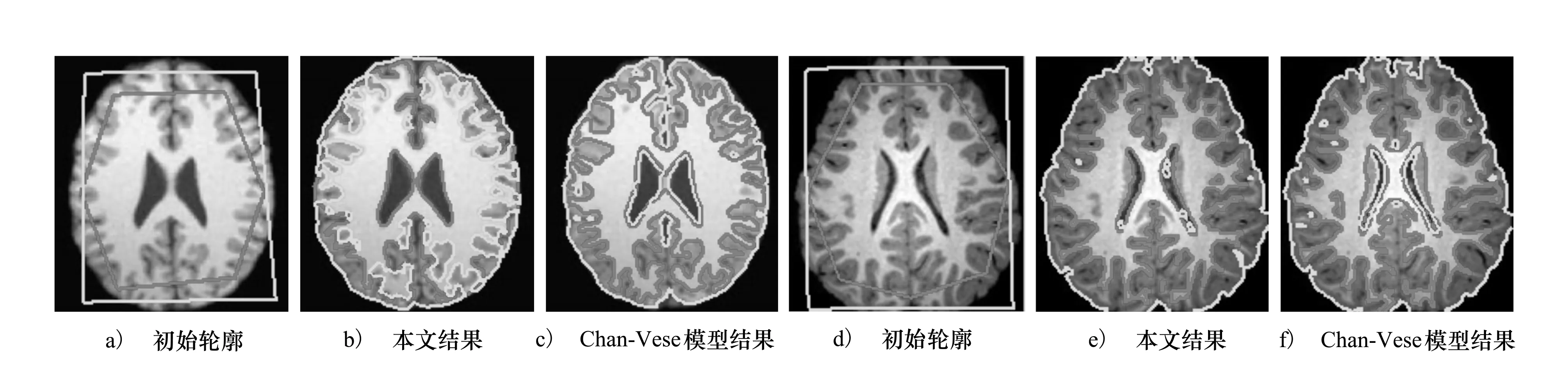
图4 灰度不均匀图像分割

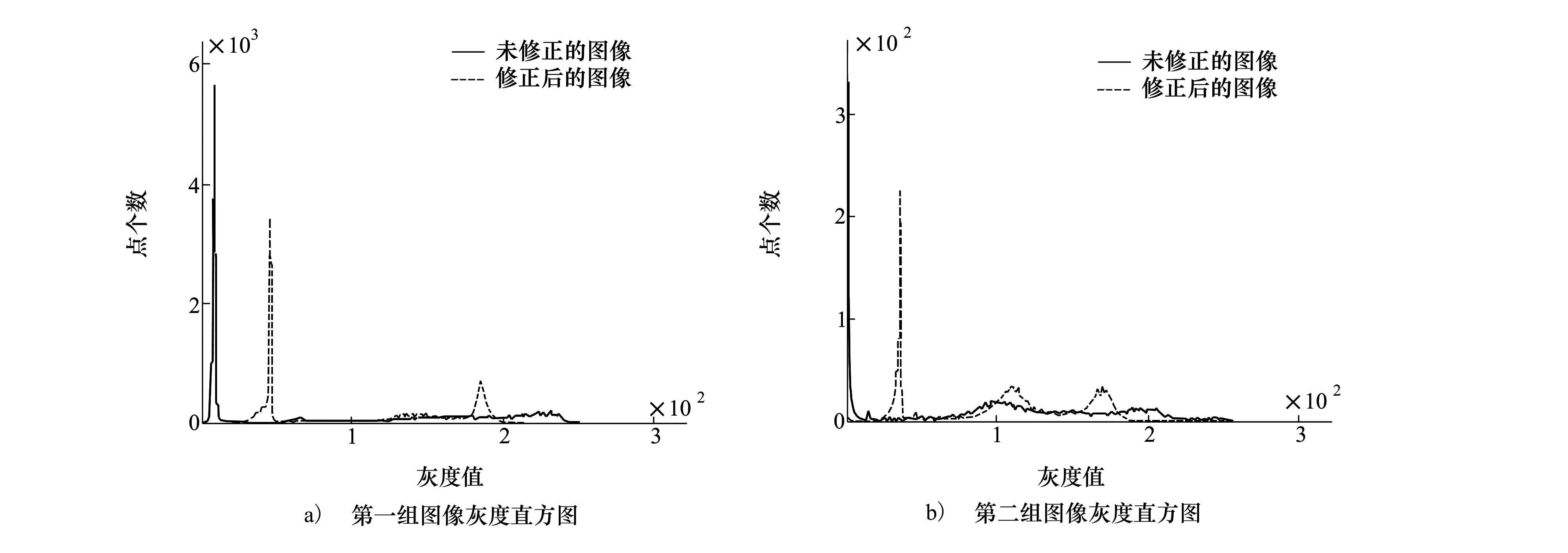
图5 修正前后图像的灰度直方图

4 结 论

本文针对图像分割中的灰度不均匀及多相分割时演化曲线的越界现象,提出了一种基于边缘信息与偏移场矫正的图像多相分割模型。首先,利用对数变换将乘性偏移场转化成线性偏移场,通过核函数将区域灰度信息引入到偏移场中,利用变分法建立了基于区域信息的偏移场矫正模型。其次,利用水平集函数与图像梯度的方向信息对传统的边缘指示函数进行了改进,综合运用了图像的梯度信息,重建了边缘指示函数。此外,引入了能量惩罚项,避免了复杂的、耗时的重新初始化程序,提高了曲线的演化速度。人工合成图像和真实图像的分割实验结果表明,本文所提出模型与多相Chan-Vese模型相比,不但增强了模型对初始轮廓曲线位置的鲁棒性,同时在一定程度上加强了模型对噪声的抑制能力,而且在分割灰度不均匀的图像时也能取令人满意的分割结果。

参考文献：

[1] Chan T F, Vese L. Active Contours without Edge[J]. IEEE Trans on Image Processing, 2001, 10(2):266-277

[2] Vese L, Chan T F. A Multiphase Level Set Framework for Image Segmentation Using the Mumford and Shah Model[J]. International Journal of Computer Vision, 2002,50(3):271-293

[3] 黄保山,滕炯华. 基于偏移场修正的C-V模型水平集图像分割算法[J]. 西北工业大学学报.2013,31(2):218-222

Huang Baoshan, Teng Jionghua. A Novel Algorithm of Level Set Image Segmentation Based on Bias Field Correction C-V Model[J]. Journal of Northwestern Polytechnical University, 2013, 31(2):218-222 (in Chinese)

[4] Li Chunming, Xu Chengyang. Distance Regularized Level Set Evolution and Its Application to Image Segmentation[J]. IEEE Trans on Image Process 2010,12(12): 3243-3254

[5] Li Chunming, Kao Chiyue. Minimization of Region-Scalable Fitting Energy for Image Segmentation[J]. IEEE Trans on Image Processing, 2008, 17(10): 1940-1949

[6] Wang Li, Li Chunming. Active Contours Driven by Local and Global Intensity Fitting Energy with Application to Brain MR Image Segmentation[J]. Computerized Medical Imaging and Graphics, 2009, 33(7): 520-531

[7] Li C, Xu C, Gui C, et al. Level Set Evolution without Re-Initialization: A New Variational Formulation [C]∥IEEE International Conference on Computer Vision and Patttern Recognition (CVPR), 2005, 1: 430-436