SST-SAS在小分离流动数值模拟中的表现测试

王翔宇, 李栋

(西北工业大学 翼型叶栅空气动力学国防科技重点实验室, 陕西 西安 710072)

作为一种LES/RANS混合方法,分离涡模拟[1](DES)将湍流模型中实时变化的长度尺度作为转换器,在边界层内流动仍由RANS模化,并未显著增大计算量;在远场分离区RANS湍流模型方程转化为类亚格子模型的形式,大大降低了湍流黏性,起到了LES隐式滤波的效果。早期的DES可能出现由于边界层内模化应力不足导致的网格诱导分离现象[2](GIS),不恰当的网格分布使得边界层也受到LES控制出现了非物理解。为此,文献提出了延迟分离涡模拟[3](DDES),通过引入控制函数延迟RANS的作用范围,保证了边界层内的RANS求解。但与此同时,延迟RANS使得上游较大的湍流黏性进一步干扰了下游LES对湍流的可解能力,湍流发展受到抑制,灰区(grey area)效应[4]加剧。

借鉴DES中长度尺度的思路,Menter基于两方程类湍流模型提出了一种尺度自适应模拟方法[5](SAS)。通过引入可根据当地流动拓扑自动调整的von Karman尺度,依靠流动状态动态地自适应调整湍流黏性。从2003年至今,这种极具潜力的RANS/LES混合方法越来越得到研究者的重视。一个很好的例子就是CFD领域广泛应用的ANSYS Fluent软件在2010年发布的13.0版本中一度采用SAS取代了DES出现在湍流模型的选择面板中(DES方法仍然被保留,但被隐藏了)。基于此,本文分别采用SST-SAS、SST-DES和SST-DDES 3种方法对AS239翼型最大升力点临界状态进行数值模拟,同时关注了最终得到的翼型表面边界层和尾迹区自由剪切层的流动信息,考核了SAS与DES类方法之间的表现差异。

1 SST-SAS模型方程

根据文献[6],SST-SAS事实上只在标准SST湍流模型中ω方程的源项中增加了一项QSAS

(1)

(2)

(3)

式中：Lvk和L分别代表von Karman尺度和模化湍应力尺度。Menter指出[5],Lvk一方面能够覆盖惯性子区所有的湍流脉动尺度,另一方面能够在非稳态区根据当前已知流场分辨漩涡动态,实时调整湍流模型中的长度尺度,在自适应全流场网格的基础上准确体现了局部流动尺度(特别在边界层内)。事实上对SST-SAS整体而言,通过Lvk将流动分为了RANS区(QSAS=0)和SAS区(QSAS>0),当流动进入分离状态时,QSAS增大,即增大了ω方程的生成项,加剧了湍流黏性的耗散从而促进了分离流动的发展。

需要特别说明的是,标准的SST-SAS模型在实际使用中出现了高波数耗散不足的问题。根据上文的介绍,引入的von Karman尺度Lvk表征这流场的最小漩涡分辨尺度并以此得到足够小的湍流黏性去产生更小的漩涡,直到漩涡小到网格的分辨率为止——这是一种理想的情况,事实上由于SST-SAS的控制方程中并没有提供流动单元截断波数的信息,在达到截断波数后由大到小传递的漩涡尺度超过了网格的分辨极限,耗散很小(Lvk很小,QSAS很大)但与漩涡对应的湍动能在截断波数处停止传递(k方程不受Lvk控制),导致湍动能在高波数附近积累,当网格数相同时,雷诺数越大网格的分辨率越低,湍动能积累越大,湍流模型方程生成项耗散项严重不平衡,影响了SST-SAS的数值稳定性。根据Menter的建议[6],本文采用下面的公式对Lvk限制

Lvk=max(κS/|2U|,·Δ)

(4)

限于篇幅,关于SST-DES和SST-DDES的具体介绍本文不再赘述,可参考文献[2-3]。

2 算例选择与结果分析

AS239翼型临界状态是一个经典的小分离流动算例[7-8]。实验显示在来流Ma=0.15,Re=2×106条件下当迎角为13.3°时翼型达到最大升力点,分离发生在尾部很小范围且分离涡尺度很小。在此计算条件下,本文算例中流向二维切面C网格为323×121,远场约为25c,壁面法向第一层网格距离约为1×10-5c,三维展向拉伸距离为0.5c,共40层。时间推进采用基于LU-SGS的双时间步长法,真实时间步设为0.01c/U∞。

图1 涡量分布云图

图1给出了3种方法得到的涡量分布。整体定性来看,由于网格诱导分离SST-DES在翼型中部位置即出现了明显的大分离漩涡并不断向下游发展——这与实验观察到的临界状态小分离是相背离的。SST-DDES虽然避免了流动在翼型表面的提前分离但延迟RANS使得尾迹区漩涡发展受到抑制变得模糊不清。相比之下,SST-SAS在翼型表面涡量分布与SST-DDES类似而在后缘的自由有剪切层的漩涡运动更加清晰细密。

图2和图3给出了在上述计算条件下翼型表面压力因数和摩擦阻力因数分布(右上角小图为局部放大)。相比于实验得到分离点约0.82c,SST-DES仅为0.7c左右,尾部边界层内模化应力严重不足,而SST-DDES和SST-SAS分离点均处在0.8c之后,表面压力分布也非常类似,有效减轻了网格诱导分离的影响——这一点可以从图4翼型表面3个站位的速度分布得到进一步印证。

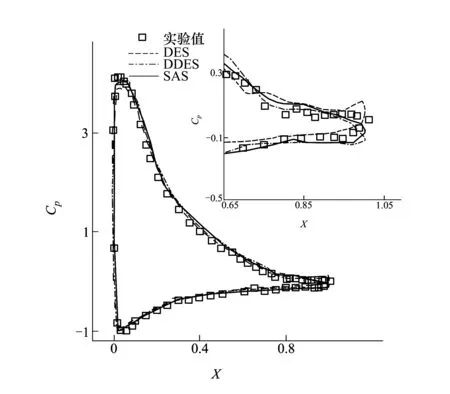
图2 翼型表面压力因数分布

图3 表面摩擦阻力因数分布

从图5翼型后缘尾迹区的流向速度分布不难看出,延迟RANS 使得DDES在尾迹区特别是靠近在翼型的位置湍流黏性偏大,模化剪切应力偏大,流向黏滞最强。SAS受到灰区的影响明显较小,和DES流向速度分布类似。而对于图6,由于DES提前分离所卷起的较大漩涡(图1a),其法向速度分布与实验值的偏差明显大于SAS的结果。

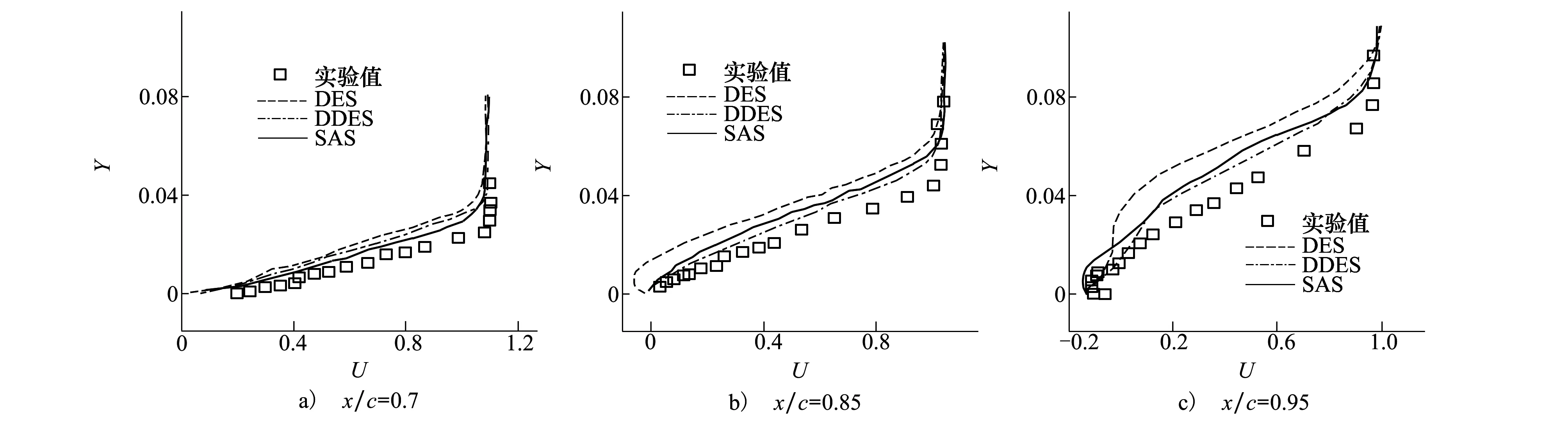
图4 翼型表面流向速度分布

图5 翼型尾迹区流向速度分布

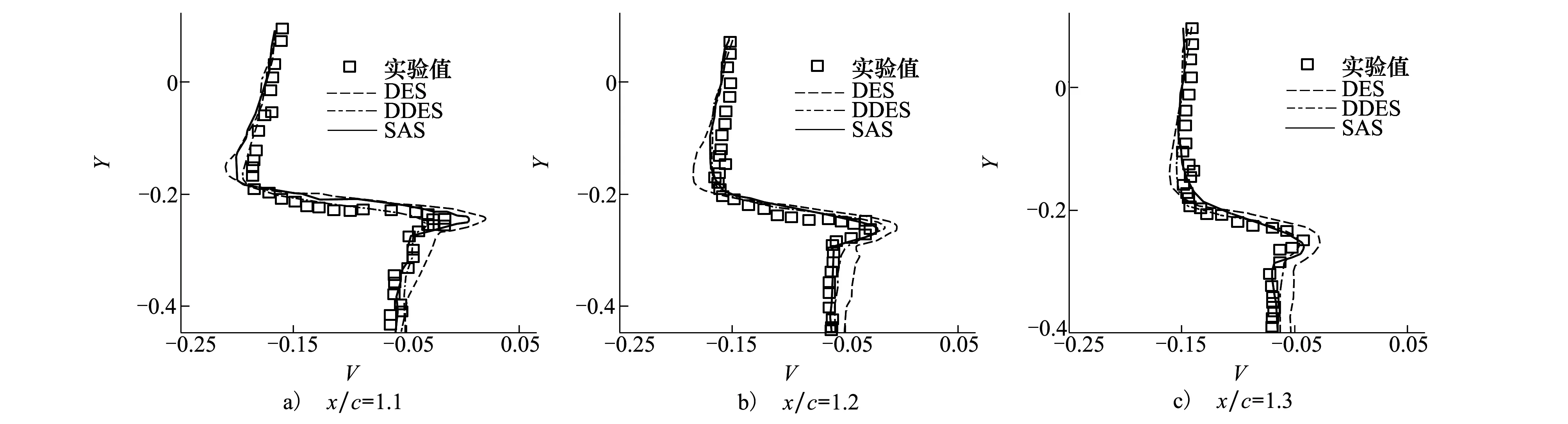
图6 翼型尾迹区法向速度分布

3 结 论

本文以AS239翼型最大升力点临界状态为数值算例,测试了当前得到较多关注的新RANS/LES混合方法——SST-SAS在小分离流动中的表现。结果显示,一方面在翼型边界层处SST-SAS能够克服SST-DES中的网格诱导分离现象,得到类似SST-DDES延迟RANS的效果,另一方面在翼型尾迹区抑制了SST-DDES所表现出的强烈灰区效应影响,分离涡更加清晰细密同时速度型分布与实验结果更加接近。总体来看相比于DES类方法,在本文的测试内容内SST-SAS表现出了更为理想的数值特性。

参考文献：

[1] Spalart P R. Strategies for Turbulence Modeling and Simulations[J]. Int J Heat Fluid Flow, 2000, 21:252-263

[2] Spalart P R, Deck S, Shur M L, Squires K D. A New Version of Detached-Eddy Simulation, Resistant to Ambiguous Grid Densities[J]. Comput Fluid Dyn, 2006, 20:181-195

[3] Strelets M. Detached Eddy Simulations of Massively Separated Flows[R]. AIAA Paper, 2001, 2001-0879

[4] Michel U, Eschricht D, Greschner B, et al. Advanced DES Methods and Their Application to Aeroacoustics[C]∥Progress in Hybrid RANS-LES Modelling, 2010: 59-76

[5] Menter F R, Kuntz M, Bender R. A Scale-Adaptive Simulation Model for Turbulent Flow Predictions[R]. AIAA Paper, 2003: 2003-0767

[6] Egorov Y, Menter F R. Development and Application of SST-SAS Turbulence Model in the DESIDER Project[C]∥Progress in Hybrid RANS-LES Modelling, 2008: 261-270

[7] Christian Gleyzes, Patrick Capbern. Experimental Study of Two Airbus/ONERA Airfoils in Near Stall Conditions[J]. Aerospace Science and Technology, 2003, 7: 439-449

[8] Stefan Schmidtf, Rank Thiele. Detached Eddy Simulation of Flow around A-Airfoil[J]. Flow, Turbulence and Combustion, 2003, 71: 261-278